From Gs-monoidal to Oplax Cartesian Categories: Constructions and Functorial Completeness

Abstract

Originally introduced in the context of the algebraic approach to term graph rewriting, the notion of gs-monoidal category has surfaced a few times under different monikers in the last decades. They can be thought of as symmetric monoidal categories whose arrows are generalised relations, with enough structure to talk about domains and partial functions, but less structure than cartesian bicategories. The aim of this paper is threefold. The first goal is to extend the original definition of gs-monoidality by enriching it with a preorder on arrows, giving rise to what we call oplax cartesian categories. Second, we show that (preorder-enriched) gs-monoidal categories naturally arise both as Kleisli categories and as span categories, and the relation between the resulting formalisms is explored. Finally, we present two theorems concerning Yoneda embeddings on the one hand and functorial completeness on the other, the latter inducing a completeness result also for lax functors from oplax cartesian categories to $\textbf{Rel}$.

Appendices

Appendix A Lax/oplax/bilax Monoidal Functors

This section recalls the definitions of lax, colax, and bilax monoidal functors, see e.g. [1]. Throughout, $\mathcal {C}$ and $\mathcal {D}$ are symmetric monoidal categories with tensor functor $\otimes$ and monoidal unit I, and we assume that $\otimes$ strictly associates without loss of generality in order to keep the diagrams simple. Left and right unitors are denoted by $\lambda$ and $\rho$, respectively,⁷ and braidings by $\gamma$.

Definition A1

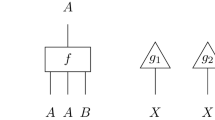
A functor $F :\mathcal {C} \rightarrow \mathcal {D}$ is lax monoidal if it is equipped with a natural transformation

$$\begin{aligned}\psi :\otimes \circ \, (F\times F) \rightarrow F\circ \otimes \end{aligned}$$

and an arrow $\psi _0 :I \rightarrow F(I)$ such that the associativity diagrams

and the unitality diagrams commute

F is said to be lax symmetric monoidal if also the following diagram commutes

For example, if $\mathcal {C}$ is the terminal monoidal category with only one object I and ${\text {id}}_I$ as the only arrow, then F is simply a monoid in $\mathcal {D}$. We do not spell out the following dual version in full detail.

Definition A2

A functor $F :\mathcal {C} \rightarrow \mathcal {D}$ is oplax monoidal if it is equipped with a natural transformation

$$\begin{aligned}\phi :F\circ \otimes \rightarrow \otimes \circ (F\otimes F)\end{aligned}$$

and a map $\phi _0 :F(I) \rightarrow I$ satisfying axioms dual to those in Definition A1. Similarly, an oplax symmetric monoidal functor is an oplax monoidal functor such that $\phi$ commutes with the braiding $\gamma$.

We also have the notion of strong symmetric monoidal functor, which is a lax symmetric monoidal functor with invertible structure arrows, or equivalently an oplax monoidal functor with invertible structure arrows; and that of strict symmetric monoidal functor, in which the structure arrows are identities.

A monoid and comonoid structure on an object in a symmetric monoidal category often interact in a nice way, either such that they form a bimonoid or a Frobenius monoid (and sometimes both). The following definition (see [1]) generalises the former notion to functors.

Definition A3

A functor $F :\mathcal {C} \rightarrow \mathcal {D}$ is bilax monoidal if it is equipped with a lax monoidal structure $\psi ,\psi _0$ and an oplax monoidal structure $\phi ,\phi _0$ such that the following compatibility conditions hold

• Braiding. The following diagram commutes

  

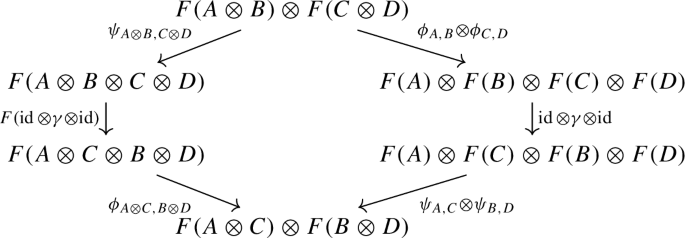
• Unitality. The following diagrams commute

  

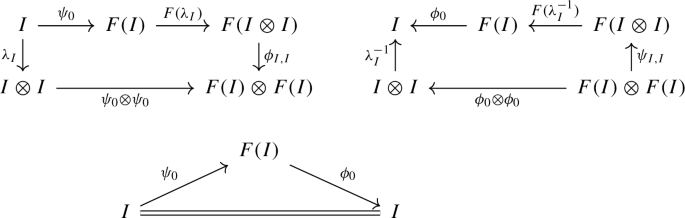
We also say that F is bilax symmetric monoidal if in addition both the lax and oplax structures are symmetric.

Appendix B Commutative Monads

A strength and a costrength for a monad on a monoidal category are structures relating the monad with the tensor product of the category at least in one direction. A monad equipped with a strength is called a strong monad. This notion was introduced by Kock in [40] as an alternative description of enriched monads. Strong monads have been successfully used in computer science, playing a fundamental role in Moggi’s theory of computation [46, 47].

We recall these concepts in the following definitions.

Definition B.1

A strong monad $(T,\mu ,\eta ,t)$ on a symmetric monoidal category $\mathcal {C}$ is a monad $(T,\mu ,\eta )$ on $\mathcal {C}$ together with a natural transformation

$$\begin{aligned} t_{X,Y} :X\otimes T(Y) \rightarrow T(X\otimes Y), \end{aligned}$$

called strength, such that the following diagrams commute for all objects X, Y, Z of $\mathcal {C}$

Example B.2

The list monad $T_{\textrm{list}} :\textbf{Set} \rightarrow \textbf{Set}$ is strong. Given two sets X and Y, the strength component

$$\begin{aligned} t_{X,Y} :X \times T_{\textrm{list}}(Y) \rightarrow T_{\textrm{list}}(X \times Y) \end{aligned}$$

is given by the function assigning to an element $(x,[y_1,\dots ,y_m]))$ of $X\times T_{\textrm{list}}(Y)$ the element $[(x,y_1),\dots ,(x,y_m)]$ of $T_{\textrm{list}}(X\times Y)$.

In fact, any monad on the cartesian category $\textbf{Set}$ is strong in a unique way, where the strength can be defined similarly to the strength of the list monad. We refer to [40] for more details.

Remark B.3

The braiding $\gamma$ of $\mathcal {C}$ let us define a costrength with components

$$\begin{aligned}t_{X,Y}' :T(X)\otimes Y \rightarrow T(X\otimes Y)\end{aligned}$$

given by

$$\begin{aligned}t_{X,Y}':=T(\gamma _{Y,X}) \circ t_{Y,X} \circ \gamma _{T(X),Y}.\end{aligned}$$

It satisfies axioms that are analogous to those of strength.

Definition B.4

A strong monad $(T,\mu ,\eta ,t)$ on a symmetric monoidal category $\mathcal {C}$ is said to be commutative if the following diagram commutes for every object X and Y

Remark B.5

It is well-known that on a symmetric monoidal category, commutative monads are equivalent to symmetric monoidal monads [40, Theorem 2.3]. Indeed, the diagonal of (B2) equips the functor T with a lax symmetric monoidal structure, whose components we denote by $c_{X,Y}: T(X) \otimes T(Y) \rightarrow T(X \otimes Y)$.