Complexity guarantees for an implicit smoothing-enabled method for stochastic MPECs

Abstract

Mathematical programs with equilibrium constraints (MPECs) represent a class of hierarchical programs that allow for modeling problems in engineering, economics, finance, and statistics. While stochastic generalizations have been assuming increasing relevance, there is a pronounced absence of efficient first/zeroth-order schemes with non-asymptotic rate guarantees for resolving even deterministic variants of such problems. We consider a subclass of stochastic MPECs (SMPECs) where the parametrized lower-level equilibrium problem is given by a deterministic/stochastic variational inequality problem whose map** is strongly monotone, uniformly in upper-level decisions. Under suitable assumptions, this paves the way for resolving the implicit problem with a Lipschitz continuous objective via a gradient-free zeroth-order method by leveraging a locally randomized spherical smoothing framework. Efficient algorithms for resolving the implicit problem allow for leveraging any convexity property possessed by the implicit problem, which in turn facilitates the computation of approximate global minimizers. In this setting, we present schemes for single-stage and two-stage stochastic MPECs when the upper-level problem is either convex or nonconvex in an implicit sense. (I). Single-stage SMPECs. In single-stage SMPECs, in convex regimes, our proposed inexact schemes are characterized by a complexity in upper-level projections, upper-level samples, and lower-level projections of ${\mathcal {O}}(\tfrac{1}{\epsilon ^2})$, ${\mathcal {O}}(\tfrac{1}{\epsilon ^2})$, and ${\mathcal {O}}(\tfrac{1}{\epsilon ^2}\ln (\tfrac{1}{\epsilon }))$, respectively. Analogous bounds for the nonconvex regime are ${\mathcal {O}}(\tfrac{1}{\epsilon })$, ${\mathcal {O}}(\tfrac{1}{\epsilon ^2})$, and ${\mathcal {O}}(\tfrac{1}{\epsilon ^3})$, respectively. (II). Two-stage SMPECs. In two-stage SMPECs, in convex regimes, our proposed inexact schemes have a complexity in upper-level projections, upper-level samples, and lower-level projections of ${\mathcal {O}}(\tfrac{1}{\epsilon ^2})$, ${\mathcal {O}}(\tfrac{1}{\epsilon ^2})$, and ${\mathcal {O}}(\tfrac{1}{\epsilon ^2}\ln (\tfrac{1}{\epsilon }))$ while the corresponding bounds in the nonconvex regime are ${\mathcal {O}}(\tfrac{1}{\epsilon })$, ${\mathcal {O}}(\tfrac{1}{\epsilon ^2})$, and ${\mathcal {O}}(\tfrac{1}{\epsilon ^2}\ln (\tfrac{1}{\epsilon }))$, respectively. In addition, we derive statements for accelerated schemes in settings where the exact solution of the lower-level problem is available. Preliminary numerics suggest that the schemes scale with problem size, are relatively robust to modification of algorithm parameters, show distinct benefits in obtaining near-global minimizers for convex implicit problems in contrast with competing solvers, and provide solutions of similar accuracy in a fraction of the time taken by sample-average approximation (SAA).

Appendix

Lemma 13

(cf. Lemma 10 in [82] and Lemma 2.14 in [40]) Let $\ell$ and N be arbitrary integers where $0\le \ell \le N-1$. The following hold.

• (a) $\ln \left( \frac{N+1}{\ell +1}\right) \le \sum _{k=\ell }^{N-1}\frac{1}{k+1} \le \frac{1}{\ell +1}+\ln \left( \frac{N}{\ell +1}\right)$.

• (b) If $0\le \alpha <1$, then for any $N \ge 2^{\frac{1}{1-\alpha }}-1$, we have $\frac{(N+1)^{1-\alpha }}{2(1-\alpha )} \le \sum _{k=0}^{N}\frac{1}{(k+1)^\alpha }\le \frac{(N+1)^{1-\alpha }}{1-\alpha }$.

Lemma 14

(Theorem 6, p. 75 in [41]) Let $\{u_t\}\subset {\mathbb {R}}^n$ denote a sequence of vectors where $\lim _{t \rightarrow \infty }u_t=\hat{u}$. Also, let $\{\alpha _k\}$ denote a sequence of strictly positive scalars such that $\sum _{k=0}^{\infty } \alpha _k = \infty$. Suppose $v_k\in {\mathbb {R}}^n$ is defined by $v_k \triangleq \frac{\sum _{t=0}^{k}\alpha _t u_t}{\sum _{t=0}^{k}\alpha _t}$ for all $k\ge 0$. Then, $\lim _{k\rightarrow \infty }v_k = \hat{u}$.

Lemma 15

(cf. [65]) Let $v_k,$ $u_k,$ $\alpha _k,$ and $\beta _k$ be nonnegative random variables, and let the following relations hold almost surely:

$$\begin{aligned}&{\mathsf {E}}\!\left[ v_{k+1}\mid {{\tilde{{\mathcal {F}}}}_k}\right] \le (1+\alpha _k)v_k - u_k + \beta _k \quad \hbox {for all} k, \quad \sum _{k=0}^\infty \alpha _k< \infty ,\quad \sum _{k=0}^\infty \beta _k < \infty , \end{aligned}$$

where ${\tilde{{\mathcal {F}}}}_k$ denotes the collection $v_0,\ldots ,v_k$, $u_0,\ldots ,u_k$, $\alpha _0,\ldots ,\alpha _k$, $\beta _0,\ldots ,\beta _k$. Then, we have almost surely $\lim _{k\rightarrow \infty }v_k = v$ and $\sum _{k=0}^\infty u_k < \infty ,$ where $v \ge 0$ is some random variable.

Proof of Lemma 8

We use induction on k for $k\ge 0$. We have $e_0 =\tfrac{\Gamma e_0}{0+\Gamma } \le \tfrac{\max \left\{ \tfrac{\beta \gamma ^2}{\alpha \gamma -1},\Gamma e_0\right\} }{0+\Gamma }$ implying that the hypothesis statement holds for $k=0$. Let us assume that $e_k \le \tfrac{\theta _0}{k+\Gamma }$ for some $k\ge 0$ where $\theta _0 \triangleq \max \left\{ \tfrac{\beta \gamma ^2}{\alpha \gamma -1},\Gamma e_0\right\}$. Let the induction hypothesis hold for $k\ge 0$. We show that it holds for $k+1$ as well. We have

$$\begin{aligned}&\theta _0 \ge \tfrac{\beta \gamma ^2}{\alpha \gamma -1} \Rightarrow \theta _0 \le \gamma (\theta _0 \alpha - \beta \gamma ) \Rightarrow \tfrac{\theta _0}{k+\Gamma } \le \tfrac{\gamma (\theta _0 \alpha - \beta \gamma )}{k+\Gamma } \Rightarrow \tfrac{\theta _0}{k+\Gamma +1} \le \tfrac{\gamma (\theta _0 \alpha - \beta \gamma )}{k+\Gamma }\\&\quad \Rightarrow \tfrac{\theta _0}{(k+\Gamma +1)(k+\Gamma )} \le \tfrac{\gamma (\theta _0 \alpha - \beta \gamma )}{(k+\Gamma )^2} \Rightarrow \theta _0\left( \tfrac{1}{k+\Gamma }-\tfrac{1}{k+\Gamma +1}\right) \\&\quad \le \tfrac{\gamma (\theta _0 \alpha - \beta \gamma )}{(k+\Gamma )^2} \Rightarrow \tfrac{\theta _0}{k+\Gamma }- \tfrac{\gamma (\theta _0 \alpha - \beta \gamma )}{(k+\Gamma )^2} \le \tfrac{\theta _0}{k+\Gamma +1}\\&\quad \Rightarrow \left( 1-\alpha \tfrac{\gamma }{k+\Gamma }\right) \tfrac{\theta _0}{k+\Gamma }+ \tfrac{\beta \gamma ^2}{(k+\Gamma )^2} \le \tfrac{\theta _0}{k+\Gamma +1} \Rightarrow \left( 1-\alpha \gamma _k\right) \tfrac{\theta _0}{k+\Gamma }+ \beta \gamma _k^2 \le \tfrac{\theta _0}{k+\Gamma +1}\\&\quad \Rightarrow \left( 1-\alpha \gamma _k\right) e_k+ \beta \gamma _k^2 \le \tfrac{\theta _0}{k+\Gamma +1} \Rightarrow e_{k+1} \le \tfrac{\theta _0}{k+\Gamma +1}. \end{aligned}$$

$\square$

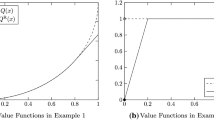
1.1 Academic examples and their stochastic counterparts in Sect. 5.4

• Problem 1. This problem is described in [61, Definition 4.1]

  $$\begin{aligned} f({{\mathbf {x}}},{{\mathbf {y}}})=r_1(x)-xp(x+y_1+y_2+y_3+y_4), \end{aligned}$$

  where $r_i(v)=c_iv+\tfrac{\beta _i}{\beta _i+1}K_i^{1/\beta _i}v^{(1+\beta _i)/\beta _i}$, $p(Q)=5000^{1/\gamma }Q^{-1/\gamma }$, $c_i$, $\beta _i$, $K_i$, $i=1,\ldots ,5$ are given positive parameters in Table 12, $\gamma$ is a positive parameter, $Q=x+y_1+y_2+y_3+y_4$.

  $$\begin{aligned} {\mathcal {X}}= & {} \{0\le x \le L\}. \\ F({{\mathbf {x}}},{{\mathbf {y}}})= & {} \left( \begin{aligned} \nabla r_2(y_1)-p(&Q)-y_1\nabla p(Q) \\&\vdots \\ \nabla r_5(y_4)-p(&Q)-y_4\nabla p(Q) \end{aligned} \right) . \\ {\mathcal {Y}}= & {} \{0\le y_j \le L, \quad j=1,2,3,4\}. \end{aligned}$$

  The following three examples were tested in [20, 61].

• Problem 2.

  $$\begin{aligned} f({{\mathbf {x}}},{{\mathbf {y}}})= & {} x_1^2-2x_1+x_2^2-2x_2+y_1^2+y_2^2. \\ {\mathcal {X}}= & {} \{0\le x_i \le 2, \quad i=1,2\}. \\ F({{\mathbf {x}}},{{\mathbf {y}}})= & {} \left( \begin{aligned} 2y_1-2x_1 \\ 2y_2-2x_2 \end{aligned} \right) . \\ {\mathcal {Y}}= & {} \{(y_j-1)^2 \le 0.25, \quad j=1,2\}. \end{aligned}$$

• Problem 3.

  $$\begin{aligned} f({{\mathbf {x}}},{{\mathbf {y}}})= & {} 2x_1+2x_2-3y_1-3y_2-60+R[\max \{0,x_1+x_2+y_1-2y_2-40\}]^2. \\ {\mathcal {X}}= & {} \{0\le x_i \le 50, \quad i=1,2\}. \\ F({{\mathbf {x}}},{{\mathbf {y}}})= & {} \left( \begin{aligned} 2y_1-2x_1+40 \\ 2y_2-2x_2+40 \end{aligned} \right) . \\ {\mathcal {Y}}= & {} \{-10\le y_j \le 20, \ x_j-2y_j-10 \ge 0, \quad j=1,2\}. \end{aligned}$$

• Problem 4.

  $$\begin{aligned} f({{\mathbf {x}}},{{\mathbf {y}}})= & {} \tfrac{1}{2}((x_1-y_1)^2+(x_2-y_2)^2). \\ {\mathcal {X}}= & {} \{0\le x_i \le 10, \quad i=1,2\}. \\ F({{\mathbf {x}}},{{\mathbf {y}}})= & {} \left( \begin{aligned} -34&+2y_1+\tfrac{8}{3}y_2 \\ -24.25&+1.25y_1+2y_2 \end{aligned} \right) . \\ {\mathcal {Y}}= & {} \{-x_{3-j}-y_j+15 \ge 0, \quad j=1,2\}. \end{aligned}$$

  The next problem is taken from [20, 62]. In all tests, the only difference lies in the objective function.

• Problem 5.

  $$\begin{aligned} {\mathcal {X}}= & {} \{0\le x \le 10\}. \\ F({{\mathbf {x}}},{{\mathbf {y}}})= & {} \left( \begin{aligned} (1+0.2x)y_1-(3+1.333x)-0.333y_3+2y_1y_4-y_5 \\ (1+0.1x)y_2-x+y_3+2y_2y_4-y_6 \\ 0.333y_1-y_2+1-0.1x \\ 9+0.1x-y_1^2-y_2^2 \\ y_1 \\ y_2 \end{aligned} \right) . \\ {\mathcal {Y}}= & {} \{y_j \ge 0, \quad j=3,4,5,6\}. \end{aligned}$$

• High-dimensional stochastic counterparts. Consider the stochastic N-dimensional counterpart of Problem 1, defined as follows.

  $$\begin{aligned} f({{\mathbf {x}}},{{\mathbf {y}}})={\mathbb {E}}\left[ r_1(x)-xp\left( x+\sum _{i=1}^n y_i,\omega \right) \right] , \end{aligned}$$

  where $r_i(v)=c_iv+\tfrac{\beta _i}{\beta _i+1}K_i^{1/\beta _i}v^{(1+\beta _i)/\beta _i}$, $p(Q,\omega )=5000^{1/\gamma (\omega )}Q^{-1/\gamma (\omega )}$, $c_i = 6$, $\beta _i=1$, $K_i = 5$, $i=1,\ldots ,5$, $\gamma (\omega ) \in {\mathcal {U}}(0.9,1.1)$ is a positive parameter, $Q=x+\sum _{i=1}^N y_i$.

  $$\begin{aligned} {\mathcal {X}}= & {} \{0\le x \le L\}. \\ F({{\mathbf {x}}},{{\mathbf {y}}},\omega )= & {} \left( \begin{aligned} \nabla r_2(y_1)-p(&Q,\omega )-y_1\nabla p(Q,\omega ) \\&\vdots \\ \nabla r_n(y_n)-p(&Q,\omega )-y_n\nabla p(Q,\omega ) \end{aligned} \right) . \\ {\mathcal {Y}}= & {} \{0\le y_j \le L, \quad j=1,\ldots , n\}. \end{aligned}$$

  The stochastic N-dimensional counterpart of Problem 2.

  $$\begin{aligned} {\mathbb {E}}[f({{\mathbf {x}}},{{\mathbf {y}}}(\omega ))], \text{ where } f(x,y(\omega ))= & {} \Vert x - \mathbf{1}\Vert ^2 + \Vert y(\omega )\Vert ^2. \\ {\mathcal {X}}= & {} \{0\le x_i \le 2, \quad i=1,\ldots , n\}. \\ F({{\mathbf {x}}},{{\mathbf {y}}},\omega )= & {} \left( \begin{aligned} 2y - 2x + \omega \end{aligned} \right) . \\ {\mathcal {Y}}= & {} \{\Vert y-\mathbf{1}\Vert ^2 \le 0.25 \}{, \text{ where } \omega \in {\mathcal {U}}(-0.5,0.5).} \end{aligned}$$

Table 12 Parameter specification for Problem 1