Introduction

Since the beginning of the year 2020, the whole world has faced a great health challenge unprecedented in humanity because the outbreak of the COVID-19 pandemic due to the new coronavirus (SARS-CoV-2). The total worldwide number of infections as of 07 December 2022 is over 641 million confirmed cases and more than 6.6 million deaths [1]. In Mexico, as of 7 December 2022 are over 7.1 million confirmed infections and more than 331 thousand deaths [2]. To mitigate COVID-19 infections and reduce the mortality rate, several epidemiological researchers and virologists from various world regions have developed and tested alternative anti-COVID-19 treatments. Among the most widely applied treatments against the coronavirus because of their effectiveness are those that use the drugs ribavirin [3], chlorpromazine [4], favipiravir [5], remdesivir [6], chloroquine [7], and hydroxychloroquine [8]. Even when the World Health Organization (WHS) has not recommended any of these drugs as treatment for COVID-19, health organizations and hospitals in several countries, including the USA and Mexico, have used chloroquine (CQ) and hydroxychloroquine (HCQ) as an alternative anti-COVID-19 treatment to mitigate the death rate because of their effectiveness against malaria virus and anti-inflammatory properties [9]. However, these drugs fall in the category of persistent contaminants of water because of their low biodegradability. CQ is an anti-inflammatory drug like ibuprofen but with a broader spectrum [10]. The chemical structure of CQ is depicted in Table 1, and it belongs to the group of aminoquinolines [11]. It is a white, odorless, and crystalline powder with a bitter taste, which is soluble in water and highly soluble in chloroform and ether [12]. This drug is highly toxic and can cause seizures, coma, and heart failure [11] at doses greater than 220 mg kg−1 [13]. Due to CQ poorly biodegradability, it cannot be treated in conventional wastewater treatment plants (e.g., activated sludge), in this sense, the advanced oxidation processes (e.g., electro-oxidation, photodegradation, among others) are most appropriate to remove this type of pollutants because of their effectiveness since a 90% of degradation is achieved [14]. There are few studies on assisted degradation of CQ in an aqueous environment, which mainly focus on photochemical stability [15], alkaline hydrolysis and chemical oxidation with H2O2 [16], electro-Fenton [17], and photodegradation [18]. Electrochemical degradation is a green technology that has been rising interest in the last years because of its low energy consumption and high effectiveness in the degradation of persistent pollutants such as 4-chlorophenol [19], 2-chlorophenol [20], and ibuprofen [21], among others [22, 23]. Although there are few degradation studies (photodegradation and electro-Fenton) of CQ, which employ anodes of graphite, Pt, and BDD to produce hydrogen peroxide (H2O2) as an oxidant agent, the optimization of the degradation of CQ has not been reported. Also, the electro-oxidation has not been yet employed to perform the degradation of CQ. In this context, BDD anodes have negligible interaction with the hydroxyl radical (●OH) generated on their surface [24] implying high oxidation efficiency [25]. Additionally, electro-oxidation does not require any additional reagents because only uses electrical energy as a unique reagent [21], where the electron flow is the green reagent [26] that drives the electrolysis process to produce ●OH.

Table 1 Synthetic wastewater quality and physical properties of CQ
Full size table

Concerning the optimization of the electrochemical processes, many works employ the response surface methodology (RSM) as a popular method. RSM is mainly driven by experimental designs, which include central composite rotatable (CCR) [27], Box-Behnken [28], Taguchi [29], Plackett–Burman [30], and others [31, 32]. CCR design is the most used because provides sufficient data for testing a lack of fit. In the electrochemical degradation of emerging pollutants through optimization DoE-driven, the studied standard variables include the initial potential of hydrogen (pH0), current intensity (I), or current density (j), initial concentration ([C]0), for batch reactors the stirring speed (Ω), and for flow-by reactors, the volumetric flow rate (Q), while the common responses are electrochemical degradation efficiency (η) [33], color removal efficiency (%CR) [34], COD removal efficiency (%COD) [35], TOC removal efficiency (%TOC) [36], and energy consumption (EC) [21]. Although the literature on parametric optimization by RSM is abundant, convex optimization has not been widely addressed in the electrochemical degradation processes even though it is widely implemented by students and researchers from industry and academia.

In this work, the maximizing electrochemical degradation of chloroquine phosphate (EDCQ) was carried out in a FBER in batch recirculation mode by the convex optimization method. The FBER is equipped with two BDD electrodes. To complete the optimization objective a CCRD was used to model and evaluate the effect on the degradation efficiency of many operating variables, namely initial pH, current density (j), and liquid volumetric flow rate (Q). Also, the total operating cost, model validation, and kinetic modeling were computed. This research is justified in the context of the intensive use assumption of CQ as an anti-COVID-19 drug and significant production of pharmaceutical wastewater.

Materials and methods

Reagents and aqueous chloroquine phosphate solution

All reagents were commercially available and used as received. The chloroquine phosphate (CQ), sodium hydroxide (NaOH), and sulfuric acid (H2SO4) were purchased from Sigma-Aldrich Company, with a purity of 98.5%, 97%, and 95%, respectively. Meanwhile, the sodium sulfate (Na2SO4) was purchased from Karal Group with a purity of 99%.

Synthetic wastewater of CQ (150 mg L−1 or 62.81 mg of TOC L−1) with 0.1 M of Na2SO4 as a supporting electrolyte was freshly prepared each day for each experiment. This synthetic solution was then added into the reservoir of the experimental set-up to homogenize it by recirculating it for 10 min through the experimental set-up without applying any current density. Additionally, distillate water was used for preparing all synthetic wastewater solutions of CQ. Table 1 displays the chemical structure and physicochemical properties of CQ.

Experimental system

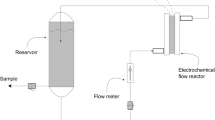
The experimental system was made-up of a flow-by electrochemical reactor (active area of 32 cm2, interelectrode gap of 1.1 cm, and effective volume of 35.2 cm3) provided with two BDD electrodes, a polycarbonate vessel tank (volume of 3.5 L), a magnetic pump of 300 rpm, a glass rotameter, a tubing of 0.635 cm radius, and valves and connectors of Master-FlexMT quality. A full description can be found in an authors’ previous work [41]. A representative chart diagram of the experimental system is depicted in Fig. 1.

Fig. 1
figure 1

Experimental system for the EDCQ in a flow-by reactor under batch recirculation mode

Full size image

Electrochemical degradation of CQ

A total of 2.5 L of aqueous CQ solution (Vs) were added into the reservoir of the experimental system (see Fig. 1). The analyzed operational variables were initial pH (pH0), current density (j), and liquid flowrate (Q), according to Table 2. The lower, center, higher, and axial levels of each operational factor that appeared in Table 2 are coded as − α, − 1, 0, + 1, and + α, respectively.

Table 2 Numeric values and levels of the operating factor
Full size table

The design space and the 17 runs for the optimization of the electrochemical degradation process of CQ are presented in Table 3. The experimental design was a central composite rotatable one (CCRD, 8 factorial points, 6 axial points, and 3 center points, where α =  ± 1.68, giving 17 runs).

Table 3 CCRD of initial pH (X1), current density (X2), liquid flowrate (X3), and their observed response (degradation efficiency (η), %) using a FBER
Full size table

In an electrochemical process, the potential of hydrogen (pH) is one of the most important variables since the process is conducted in an aqueous solution. Therefore, pH must be chosen according to the hydrophilic and lipophilic properties of the contaminant to be degraded; in this case, the pH must be lower than 11.5 since the solubility decreases at higher values than 11.5, the current density (j) was specified by a typical range used in the electro-oxidation processes [22], the range of volumetric flow rate (Q) was selected according to previous authors works, where other organic molecules (e.g., ibuprofen and 2-chlorophenol) have been degraded with the same reactor [20, 21]. The operational factors analyzed on this research can be encrypted by applying Eq. (1),

$$x_{i} = \frac{{X_{i} - X_{i,0} }}{{\Delta X_{i} }}$$
(1)

Chemical analysis

The absorption spectra for each run of the CCRD were obtained and recorded after 9 h of treatment using a Lamda 365 PerkinElmer UV–visible spectrophotometer, UV–visible spectra of the synthetic solution of CQ at 150 mg L−1 in 0.1 M Na2SO4 were initially recorded. The absorption spectra of the same solution were then recorded at different times when the FBER operate under optimal operating conditions. Also, all UV–visible spectra of samples were acquired between 200 and 400 nm, identifying 220 nm as the wavelength of maximum absorption of CQ. COD was determined according to standard methods for the analysis of wastewater [42], and the total organic carbon (TOC) was measured by a 6001 TOC analyzer Shimadzu for the optimal operating point of the electrochemical degradation of CQ. The pH of all synthetic wastewater solutions of CQ was measured by using a HI2210 Hanna potentiometer.

Analytical procedures

The degradation efficiency was computed by using Eq. (2). Energy consumption per L was estimated by using Eq. (3). The total operational cost (cost) of the CQ degradation includes energy consumption (EC (kWh L−1)) and electrolyte cost (Celectrolyte (g L−1)), which can be calculated by the set of Eqs. (3), (4), and (5). The percentage of mineralization efficiency was computed according to Eq. (6),

$$\eta \left( \% \right) = \frac{{\left[ {CQ} \right]_{0} - \left[ {CQ} \right]_{t} }}{{\left[ {CQ} \right]_{0} }} \times 100$$
(2)
$$E_{C} = \frac{{U \times j \times A_{e} \times t}}{{V_{s} }}$$
(3)
$$C_{electrolyte} = \frac{{q_{{Na_{2} SO_{4} }} }}{{V_{s} }}$$
(4)
$${\text{Cos}} t = \xi E_{C} + \phi C_{electrolyte}$$
(5)
$$ME\left( \% \right) = \frac{{TOC_{0} - TOC_{t} }}{{TOC_{0} }} \times 100$$
(6)

where U is the mean cell voltage (V), Vs is the synthetic solution volume (L), Ae is the electrode area (cm2), j is the current density (mA cm−2), t is the degradation time (h), ξ is the electricity cost (0.071 US$ (kWh)−1) provided by a Mexican Electricity company in December 2022, taking into consideration that 1 US$ (20 MXP)−1), ϕ is the price of electrolyte (0.033 US$ g−1), and q is the quantity of used chemicals (g).

Optimization process

To accomplish the optimization process, the first step was to propose a model of the observed response (η) in the function of the selected operational variables (e.g., initial pH, current density, and liquid flow rate) employing a second-order polynomial model like Eq, (7),

$$\eta = \beta_{0} + \sum\limits_{i = 1}^{k} {\beta_{i} x_{i} } + \sum\limits_{i = 1}^{k} {\beta_{ii} x_{i}^{2} } + \sum\limits_{i = 1}^{k - 1} {\sum\limits_{k = i + 1}^{k} {\beta_{i,k} x_{i} x_{k} } } + \varepsilon$$
(7)

where η is the modeled response, β values are the coefficients of the polynomial, ε is the random error, and xi and xj are the encrypted independent variables. The β values were computed by applying the stepwise regression method. To evaluate the suitability of the model fitted and the importance of the terms of the second-order polynomial an analysis of variance (ANOVA) was performed. Reduced root-mean-square error (RMSE) is often used to demonstrate the fitted model accuracy of responses (e.g., η, have a look at Eq. (8)),

$$RMSE = \sqrt {\frac{1}{n}\sum\limits_{n} {\left( {\frac{{\eta_{n,\,\,\Pr ed} - \eta_{n,\,\,Exp} }}{{\eta_{n,\,\,Exp} }}} \right)}^{2} }$$
(8)

where ηn, Pred is the modeled response, ηn, Exp is the experimental response, and n is the total amount of runs.

The second step was to write the quadratic polynomial model in matrix form equal to Eq. (9); therefore, this equation must be a concave function.

$$\,\eta = x^{T} Ax + Bx + C$$
(9)

where x = [x1, x2, …, xn]T, A, is the matrix that contains the coefficients terms of the quadratic equation; B is the vector that contains the linear coefficient terms of the quadratic equation, and C is the constant term of the quadratic equation.

The third step was to prove that Eq. (9) was a concave function by means of convex optimization. Hence, the eigenvalues (λ1, λ2, and λ3) of the Hessian matrix (H, Eq. (10)) must be equal to or less than zero.

$$H = \frac{\partial }{{\partial x^{T} \partial x}}\left( {x^{T} Ax + Bx + C} \right) = 2A$$
(10)

The fourth step was to rewrite the original optimization problem (maximization of η) in an optimization standard problem form like Eq. (11). The fifth step and last one was to solve numerically the minimization problem. To find the optimal point, the MATLAB. R2017a ® software package was employed. Also, three different algorithms (such as “active-set,” “sqp,” and “interior-point”) were used. Moreover, a general pseudo-code to solve the optimization problem given by Eq. (11) is presented in the supported material (see Table S1).

$$\begin{gathered} \,Min\,\,\,\,\,\eta = x^{T} Ax + Bx + C \hfill \\ s.t. \hfill \\ \begin{array}{*{20}c} {} & {} & {} & {x_{1}^{2} \le \alpha^{2} } \\ {} & {} & {} & {x_{2}^{2} \le \alpha^{2} } \\ {} & {} & {} & {x_{3}^{2} \le \alpha^{2} } \\ \end{array} \hfill \\ \alpha\!:\,\,rotatability\,\,\left( {1.68} \right) \hfill \\ \end{gathered}$$
(11)

Results and discussion

Model fitting

In this research, the Design Expert® V.10.0 software was employed to conduct the CCRD, regression analysis, and model fitting. The seventeen runs of the CCRD are shown in Table 3. In this case of study, runs 2, 3, 9, 10, 13, and 17 are axial points; runs 1, 4, 5, 7, 8, 11, 14, and 16 are factorial points; and runs 15, 12, and 6 are center points. The reported (See Table 3) experimental values of the degradation efficiency (η) of CQ are in the interval of 74.9–86.3%. Given the experimental response (η) in the function of the mathematical relationship between independent process factors, a second-order polynomial has been fitted (see Eq. (12)).

Equation with coded factors,

$$\begin{gathered} \eta = 78.76 + 0.21x_{1} - 3.29x_{2} + 0.33x_{3} + 0.025x_{1} x_{2} - 0.65x_{1} x_{3}\\ - 0.05x_{2} x_{3} - 0.49x_{1}^{2} + 0.94x_{2}^{2} + 0.83x_{3}^{2} \end{gathered}$$
(12)

Equation with uncoded factors,

$$\begin{gathered} \eta = 89.22 + 2.69X_{1} - 0.17X_{2} - 16.09X_{3} + 0.0002X_{1} X_{2} - 1.16X_{1} X_{3} \\- 0.004X_{2} X_{3} - 0.09X_{1}^{2} + 0.0005X_{2}^{2} + 13.29X_{3}^{2} \end{gathered}$$

Analysis of variance (ANOVA)

Table 4 shows the ANOVA results for the obtained second-order polynomial regression model. The ANOVA analysis indicates that the fitted model is statistically suitable for the representation of the electrochemical degradation of CQ at the studied process variables range (in a FBER equipped with two BDD electrodes). A model F-value of 25.56 indicates that the fitted model is significant with only a 0.01% probability that the F-value of a model this large could be due to noise since the p-value (0.0001) is less than 0.05 [43]. In this study, x2, x1x3,\(x_{1}^{2}\), \(x_{2}^{2}\), and \(x_{3}^{2}\) (p-values: 0.0001, 0.0752, 0.1011, 0.0091, and 0.0157) are significant model terms of the second-order polynomial since the p-value is very close to or less than 0.1. A lack of fit F-value of 0.5842 indicates that the lack of fit is not significant, which is reasonable since it was specified to fit the experimental response (ηExp) to a second-order polynomial. A determination coefficient (R2) value of 0.9705 for η indicates a very good model fitting [44]. Moreover, the RMSE for response (η) gives a value of 0.007 indicating that the model regression fitted (Eq. (12)) for the degradation efficiency (η) is in concordance with the experimental results. Also, the \(R_{\Pr ed}^{2}\) of 0.8202 is reasonable with the \(R_{Adj}^{2}\) of 0.9325 since the difference between both \((R_{Adj}^{2} - R_{Pred}^{2} )\) is less than 0.2. An adequate precision ratio of 16.871 means an adequate signal because this value is greater than 4 [45]. Hence, the second-order polynomial fitted here can be employed to model the response in the design space (CCRD). Furthermore, the given small value of the coefficient of variance (C.V. of 1.1% for η) revealed great accuracy of the performed tests since the C.V. was under 10%, which indicates that the model fitted has high reproducibility [46].

Table 4 ANOVA for the quadratic polynomial
Full size table

The parity plot (see Fig. 2a) and the normal percentage probability residual versus studentized residual (see Fig. 2b) demonstrate the model adequacy to predict the response (η). Figure 2a reveals a high-quality correlation between experimental response(ηExp) and predicted response (ηPred). Figure 2b shows a normal distribution because the scattering points fall within a 45-straight line. Therefore, the experimental data has a normal distribution. Furthermore, the outlier-t values lie in the range of ± 1.02, suggesting that the model fitting the response was reasonably good with practically no data register error because there is a high reproducibility. Also, no data transformation is necessary.

Fig. 2
figure 2

(a) Experimental response versus predicted response for η; (b) normal percentage probability residual versus studentized residual for η

Full size image

Interaction effects amongst operating factors

Analyzing Eq. (12) in terms of coded parameters, a negative β value in the second-order model indicates an adverse effect among operating parameters; meanwhile, a positive β value indicates a beneficial effect on its operational parameters. Analyzing the β values of Eq. (12) in coded terms, the degradation efficiency (η) had a favorable effect with x1 (j) and x3 (Q) but decreases with x1 (pH0). Similarly, the degradation efficiency increases with the interaction term between initial pH and current density x1x2 (pH0 × j) but had an unfavorable effect with interaction terms between initial pH and liquid flow rate x1x3 (pH0 × Q) and between current density and liquid volumetric flow rate x2x3 (j × Q).

To evaluate the effect of each coefficient (β values) on the quadratic model multiple regression, a Pareto analysis was performed by using Eq. (13),

$$P_{i} \left( \% \right) = \left( {\frac{{\beta_{i} }}{{\sum\limits_{i} {\left| {\beta_{i} } \right|} }}} \right) \times 100$$
(13)

Figure 3 displays the Pareto graphic analysis. The results in this figure indicate that among the variables, β0 (constant term, %) produces the largest effect (92.05%) on the response (η). Also, the term β2 (current density, mA cm−2), produces a medium effect (3.84%) on the response (η). These results suggest that the most important variable is the current density (j), and this agrees with the fact that at high current density, the hydroxyl radicals are increased.

Fig. 3
figure 3

Pareto chart analysis

Full size image

Figure 4 depicts the 2˗D contour plots of the degradation efficiency of CQ by means of electro-oxidation. In the electrochemical degradation of organic compounds (e.g., chloroquine), the pH plays an important role because it controls the hydroxyl radical. Therefore, from Fig. 4a a high electro-degradation is attained closely to 8.0 and from Fig. 4b a high electro-degradation is attained closely to 11.2. Hence, no obvious difference in degradation efficiency can be found when pH was in the range of 2.8–11.2. From Fig. 4a and b, a high electro-degradation is attained closely to 1.0 L min−1, which is consistent with the reported in other studies from electrochemical degradation of organic compounds (e.g., ibuprofen and 2-chlorophenol) using the same FBER [20, 21]. Also, from Fig. 4c, it can be seen that the degradation efficiency decreases when increases the current density (from 20 to 200 mA cm−2). This could be ascribed to the abatement of hydroxyl radicals production on the surface of the BDD electrode since other oxidant agents (e.g., O2, O3, and H2O2, 2.42 V, 2.07 V, and 1.78 V, respectively) have been produced simultaneously [47], which have lesser oxidation potential than the oxidation potential (2.8 V) of hydroxyl radicals. Additionally, Fig. 4b shows that at medium values of volumetric flow rate increase because the contaminant is relatively easy diffuse on the BDD electrode surface were there are high amount of hydroxyl radicals ready to react with the contaminant. Figure 4c shows that the degradation efficiency decreases at relatively high volumetric flow rate because the contaminant has not had enough contact time to react with the •OH formed on the BDD electrode surface. Moreover, even though a significant effect of pH on degradation efficiency was expected, in this study a moderate effect is shown. This is given by a decreased-on hydroxyl radical production on the BDD electrode surface. Hence, the hydroxyl anion (OH−) is favorable. Finally, hydroxyl radicals are expected to be produced on the BDD anode surface at acid and neutral pH and by direct oxidation of hydroxyl anion at a pH ≥ 10. This mechanism is expected to be very slow though [48].

Fig. 4
figure 4

Contour plot showing the effect of initial pH and current density (a), initial pH and liquid flow rate (b), and current density and liquid flow rate (c) on chloroquine degradation efficiency (η)

Full size image

Convex optimization of electrochemical degradation of chloroquine

The quadratic polynomial (Eq. (12) can be written in matrix form (see Eq. (14)) to determine the Hessian matrix according to Eq. (10). At this point, the eigenvalues of the Hessian matrix (see Eq. (15) are used to verify if the objective function (η) is concave. The eigenvalues of the Hessian matrix were λ1 =  − 1.13, λ2 = 1.78, and λ3 = 1.91, which indicate that the concavity of the surface (see Eq. (14)) is inconsistent [49]. Also, Eq. (14) has a negative curvature, indicating that there is a critical point [50], which is called a saddle point because their surface form is given by hyperboles. Moreover, the saddle point is a serious candidate to be an optimal point.

$$\eta = x^{T} \left[ {\begin{array}{*{20}c} { - 0.49} & {0.0125} & { - 0.325} \\ {0.0125} & {0.94} & { - 0.025} \\ { - 0.325} & { - 0.025} & {0.83} \\ \end{array} } \right]\,x + \left[ {\begin{array}{*{20}c} {0.21} \\ { - 3.29} \\ {0.33} \\ \end{array} } \right]\,x + 78.76$$
(14)
$$H = \left[ {\begin{array}{*{20}c} { - 0.980} & {0.025} & { - 0.650} \\ {0.025} & {1.880} & { - 0.050} \\ { - 0.650} & { - 0.050} & {1.660} \\ \end{array} } \right]$$
(15)

The convex optimalization problem to be solved is expressed by Eq. (16). The optimal operating point found is listed in Table 5. This table indicates that a local maximum was achieved when the convex optimalization problem was solved numerically by using different methods. All methods used find a unique optimal operating point. For this convex optimization problem, the Active-set method solves it in only seven iterations.

$$\begin{gathered} \,Min\,\,\,\,\,\eta = x^{T} \left[ {\begin{array}{*{20}c} { - 0.49} & {0.0125} & { - 0.325} \\ {0.0125} & {0.94} & { - 0.025} \\ { - 0.325} & { - 0.025} & {0.83} \\ \end{array} } \right]\,x + \left[ {\begin{array}{*{20}c} {0.21} \\ { - 3.29} \\ {0.33} \\ \end{array} } \right]\,x + 78.76 \hfill \\ s.t. \hfill \\ \begin{array}{*{20}c} {} & {} & {} & {x_{1}^{2} \le \left( {1.68} \right)^{2} } \\ {} & {} & {} & {}{x_{2}^{2} \le \left( {1.68} \right)^{2} } \\ {} & {} & {} & {x_{3}^{2} \le \left( {1.68} \right)^{2} } \\ \end{array} \hfill \\ \end{gathered}$$
(16)
Table 5 Solved convex optimization problem by using different numerical methods
Full size table

Even the objective function (η) not being strictly concave, the saddle point found can be called as a global maximum since it is the only one critical point of the objective function. Therefore, a local maximum can be called as a global maximum.

Model validation

To validate the set of optimal operating parameters found in the previous section, three complementary experiments were carried out under the optimal operating parameters found by convex optimization, predicted, and observed values are listed in Table 6. The relative error (12.14%) reported in Table 6 indicates a good approximation of optimal operating conditions by the convex optimization method. Hence, the maximum electrochemical degradation efficiency of CQ was 89.3% at a pH0 of 5.38, a j of 34.4 mA cm−2, Q of 1.42 L min−1, and 9 h of treatment time.

Table 6 Optimal operating parameters of the electrochemical degradation of CQ
Full size table

A TOC and COD analyses were performed according to the methodology described in the chemical analysis section. The initial and final values of TOC were 62.81 and 29.45 mg L−1, respectively, while the initial and final values of COD were 82.67 and 40.0 mg L−1, respectively. These values of TOC and COD achieve a mineralization efficiency and COD removal efficiency of 53.1 and 51.6%, respectively.

As has been known, the principal advantage of the advanced oxidation processes is the fact that a contaminant present in wastewater is transformed into carbon dioxide and ions. To evaluate the mineralization degree the mean oxidation number of carbon (MOC) has been computed by using Eq. (17) [51]. The MOC value must lie in the range of − 4 to + 4, and values outside this range indicate that COD or TOC was not determined correctly. Most compounds detected in aqueous solutions fall in the range of − 2 to + 3. In this case, the MOC varied from + 1.44 to + 1.96 indicating the presence of formic acid (MOC of + 2) [52]. This compound is produced during the oxidation of organic molecules and its further oxidation leads to carbon dioxide. Hence, the electrochemical process employed herein is an adequate technology to carry out the electro-oxidation of CQ.

$$MOC = 4 - 1.5\frac{COD}{{TOC}}$$
(17)

Total operational cost

In order to compute the total operating cost, firstly the energy consumption was computed (0.041 kWh L−1 or 41 kWh m−3) by using the Eq. (3) for U of 10.35 V, j of 34.4 mA cm−2, Ae of 32 cm2, t of 9 h, and Vs of 2.5 L. Consequently, the total operating cost (Cost) was computed by the set of Eqs. (3) to (4). Hence, the cost was 0.47 US$ L−1 when the FBER was operated at optimal operating conditions (pH0 of 5.38, j of 34.4 mA cm−2, Q of 1.42 L min−1 within 9 h of reaction time). This work is the only one that reports the associated cost (see Table 7).

Table 7 Electrochemical degradation of CQ under different wastewater treatment technologies
Full size table

Kinetic modelling

Assuming that the electrochemical degradation of CQ proceeds mainly via hydroxyl radicals and neglecting the adsorption effect of CQ on the BDD electrode surface [53], a pseudo-zero-order kinetic model was tested to fit the experimental data (see Eq. (18)),

$$\frac{{d\left[ {CQ} \right]}}{dt} = \underbrace {{ - k\left[ {^{\bullet}OH } \right]}}_{{ - k_{app} }} = - k_{app}$$
(18)

A decrease in the absorbance maximum band of CQ (220 nm) was observed in Fig. 5a, as a function of reaction time. This behavior indicated that the degradation of CQ occurred by the breakup of the chemical structure of CQ by reaction with ●OH produced during the electrooxidation reaction and, after that, forming other simple organic compounds. Also, this behavior suggests a constant production of ●OH. To study the kinetics of the overall reaction involved in the CQ electro-oxidation, the decline of CQ concentration was considered. Figure 5b shows the kinetic behavior of the electrochemical degradation of CQ. The behavior displayed in Fig. 5b reveals a satisfactory pseudo-zero-order kinetic rate performance. From a linear regression analysis, the kapp value of 13.14 mg L−1 h−1 (2.54 × 10−5 mol dm−3 h−1) was obtained with a determination coefficient (R2) value of 0.9943. It is worth mentioning that the reported kinetic constant is a global oxidation constant since the oxidation of the intermediates by the produced hydroxyl radicals over time was not discriminated for its calculation. Nevertheless, being a pseudo-zero order process indicates that at the beginning of the treatment (when there was only CQ), the specific reaction rate is practically the same.

Fig. 5
figure 5

(a) UV–Vis spectra for the CQ solution at different reaction times; (b) kinetic analysis for the pseudo-zero-order reaction of the CQ electrochemical degradation process

Full size image

The found results in this research have been compared with previous reports (see Table 7). The electrochemical degradation efficiency of CQ in the literature is greater than that reported in this work. However, the volume of treated wastewater solution of CQ employed in literature (from 0.01 to 0.5 L) is lower than that used in the current research (2.5 L). Likewise, the initial concentration of CQ ([CQ]0 = 150 mg L−1) used in this work is greater than that employed in all references, which goes from 26 to 125 mg L−1. Even though that 92% of TOC removal was achieved in reference [17], the volume treated (0.5 L) was 5 times lower than that employed in this work (2.5 L), and this may be the reason for the mineralization efficiency obtained in this work (52.2%) being lower than that in reference [17]. It should be noted that the current study is the only one that carries out the optimization of the degradation process of CQ and provides the associated cost (0.47 US$ L−1). Based on the results found in this green wastewater treatment, it can be concluded that this green process is suitable for CQ removal.

Conclusions

Given the results of the current research paper, the ensuing conclusions are as follows:

  • The degradation of chloroquine phosphate was successfully achieved in a flow-by electrochemical reactor employing two BDD electrodes and running in batch recirculation mode.

  • The quadratic model to predict the degradation efficiency (η) in a flow-by electrochemical reactor equipped with two BDD electrodes was developed as a function of pH0 (X1), j (X2), and Q (X3). Also, the most significant operational variable was found to be current density (j). This model is 

    $$\begin{gathered} \eta = 89.22 + 2.69X_{1} - 0.17X_{2} - 16.09X_{3} + 0.0002X_{1} X_{2} - 1.16X_{1} X_{3}\\- 0.004X_{2} X_{3} - 0.09X_{1}^{2} + 0.0005X_{2}^{2} + 13.29X_{3}^{2} \end{gathered}$$

  • The optimization of operational factors was satisfactorily attained by the convex optimization method. A global maximum (89.3%) was achieved at operational reaction conditions of pH0 = 5.38, j = 34.4 mA cm−2, and Q = 1.42 L min−1 within a treatment time of 9 h, employing an EC of 0.041 kWh L−1 with a Cost of 0.47 US$ L−1.

  • Electrochemical degradation of CQ follows a pseudo-zero-order kinetic rate when the green process operates at optimal operation reaction conditions.

  • The process evaluated in this investigation is a potential green process for wastewater treatment as it Babić S, Škorić I (2019) Thehas a low-cost (0.47 US$ L−1), and no additional reagents must be added to perform the electrochemical degradation, and it is friendly with the environment.

  • The oxidation number of organic carbon of the synthetic wastewater of CQ passed from + 1.44 to + 1.96 suggesting the presence of short-chain mono and dicarboxylic acids such as formic (MOC =  + 2).