SpringerLink
Log in

Dynamic responses of saturated functionally graded porous plates resting on elastic foundation and subjected to a moving mass using pb2-Ritz method

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

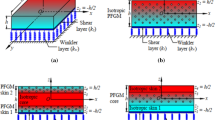
This work analyzes the dynamic responses of plates with an elastic foundation under a concentrated moving mass. The plate is made of fluid-saturated functionally graded porous material (FFGPM). The material properties of the FFGPM plate are assumed to vary smoothly across the thickness, with symmetric, asymmetric, and uniform patterns for porosity distribution. The governing equations of the FFGPM plate are developed using Reddy’s third-order shear deformation plate theory (Reddy’s TSDT), Biot’s poroelasticity theory, pb2-Ritz formulation, and the Lagrange equation. In the numerical results, the Newmark scheme is used to obtain the deflection response of the FFGPM plate with the traveling mass. Two approaches are considered and discussed, including moving load and moving mass. Moreover, the influences of the porosity coefficient, distribution patterns, different boundary conditions, elastic foundations, geometry parameters, Skempton coefficient, moving mass velocity, and the mass of moving mass on the dynamic characteristics of the FFGPM plate are studied.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

Data availability

Data will be made available upon request.

References

  1. Smith, B.H., Szyniszewski, S., Hajjar, J.F., Schafer, B.W., Arwade, S.R.: Steel foam for structures: a review of applications, manufacturing and material properties. J. Constr. Steel Res. 71, 1–10 (2012)

    Article  Google Scholar 

  2. Barbaros, I., Yang, Y., Safaei, B., Yang, Z., Qin, Z., Asmael, M.: State-of-the-art review of fabrication, application, and mechanical properties of functionally graded porous nanocomposite materials. Nanotechnol. Rev. 11(1), 321–371 (2022)

    Article  Google Scholar 

  3. Mojahedin, A., Jabbari, M., Khorshidvand, A.R., Eslami, M.R.: Buckling analysis of functionally graded circular plates made of saturated porous materials based on higher order shear deformation theory. Thin-Walled Struct. 99, 83–90 (2016)

    Article  Google Scholar 

  4. Kitipornchai, S., Chen, D., Yang, J.: Free vibration and elastic buckling of functionally graded porous beams reinforced by graphene platelets. Mater. Des. 116, 656–665 (2017)

    Article  Google Scholar 

  5. Tung, P.T., Long, N.V., Tu, T.M., Phuong, N.T.B., Hai, L.T., Long, T.N.: Nonlinear bending analysis of fgp plates under various boundary conditions using an analytical approach. Structures 34, 4803–4813 (2021)

    Article  Google Scholar 

  6. Vu, T.-V.: Mechanical behavior analysis of functionally graded porous plates resting on elastic foundations using a simple quasi-3D hyperbolic shear deformation theory-based effective meshfree method. Acta Mech. 233(7), 2851–2889 (2022)

    Article  MathSciNet  Google Scholar 

  7. Long, N.V., Tu, T.M., Truong, H.Q., Hai, L.T., Trang, V.T.T.: Displacement-based and stress-based analytical approaches for nonlinear bending analysis of functionally graded porous plates resting on elastic substrate. Acta Mech. 233(4), 1689–1714 (2022)

    Article  MathSciNet  Google Scholar 

  8. Leclaire, P., Horoshenkov, K.V., Cummings, A.: Transverse vibrations of a thin rectangular porous plate saturated by a fluid. J. Sound Vib. 247(1), 1–18 (2001)

    Article  Google Scholar 

  9. Rezaei, A.S., Saidi, A.R.: Exact solution for free vibration of thick rectangular plates made of porous materials. Compos. Struct. 134, 1051–1060 (2015)

    Article  Google Scholar 

  10. **ang, Y., Jiang, H., Lu, J.: Analyses of dynamic characteristics of a fluid-filled thin rectangular porous plate with various boundary conditions. Acta Mech. Solida Sin. 30(1), 87–97 (2017)

    Article  Google Scholar 

  11. Arani, A.G., Maraghi, Z.K., Khani, M., Alinaghian, I.: Free vibration of embedded porous plate using third-order shear deformation and poroelasticity theories. J. Eng. 2017, 1474916 (2017)

    Google Scholar 

  12. Khouzestani, L.B., Khorshidvand, A.R.: Axisymmetric free vibration and stress analyses of saturated porous annular plates using generalized differential quadrature method. J. Vib. Control 25(21–22), 2799–2818 (2019)

    Article  MathSciNet  Google Scholar 

  13. Lixian, W.: Dynamic response analysis of fluid-saturated porous rectangular plates. Zeitschrift für Naturforschung A 75(12), 1009–1023 (2020)

    Article  Google Scholar 

  14. Şimşek, M.: Nonlinear vibration analysis of a functionally graded Timoshenko beam under action of a moving harmonic load. Compos. Struct. 92(10), 2532–2546 (2010)

    Article  Google Scholar 

  15. Luong, V.H., Cao, T.N.T., Reddy, J.N., Ang, K.K., Tran, M.T., Dai, J.: Static and dynamic analyses of mindlin plates resting on viscoelastic foundation by using moving element method. Int. J. Struct. Stab. Dyn. 18(11), 1850131 (2018)

    Article  MathSciNet  Google Scholar 

  16. Sahoo, P.R., Barik, M.: A numerical investigation on the dynamic response of stiffened plated structures under moving loads. Structures 28, 1675–1686 (2020)

    Article  Google Scholar 

  17. Wang, L.A., Zhao, J., Wang, G.: Dynamic response analysis of inhomogeneous saturated soil under moving loads. Soil Mech. Found. Eng. 57(3), 211–218 (2020)

    Article  Google Scholar 

  18. Nguyen, D.K., Nguyen, Q.H., Tran, T.T., Bui, V.T.: Vibration of bi-dimensional functionally graded Timoshenko beams excited by a moving load. Acta Mech. 228(1), 141–155 (2017)

    Article  MathSciNet  Google Scholar 

  19. Jafari, P., Kiani, Y.: A four-variable shear and normal deformable quasi-3D beam model to analyze the free and forced vibrations of FG-GPLRC beams under moving load. Acta Mech. 233(7), 2797–2814 (2022)

    Article  MathSciNet  Google Scholar 

  20. Kiani, K., Nikkhoo, A., Mehri, B.: Prediction capabilities of classical and shear deformable beam models excited by a moving mass. J. Sound Vib. 320(3), 632–648 (2009)

    Article  Google Scholar 

  21. Esen, I.: A modified FEM for transverse and lateral vibration analysis of thin beams under a mass moving with a variable acceleration. Latin Am. J. Solids Struct. 14, 485–511 (2017)

    Article  Google Scholar 

  22. Awodola, T.O., Omolofe, B.: Flexural motion of elastically supported rectangular plates under concentrated moving masses and resting on bi-parametric elastic foundation. J. Vib. Eng. Technol. 6(3), 165–177 (2018)

    Article  Google Scholar 

  23. Song, Q., Liu, Z., Shi, J., Wan, Y.: Parametric study of dynamic response of sandwich plate under moving loads. Thin-Walled Struct. 123, 82–99 (2018)

    Article  Google Scholar 

  24. Rad, H.K., Ghalehnovi, M., Shariatmadar, H.: Boundary characteristic orthogonal polynomials method in the vibration analysis of multi-span plates acting upon a moving mass. Heliyon 5(6), e01919 (2019)

    Article  Google Scholar 

  25. Liu, Z., Niu, J., Jia, R.: Dynamic analysis of arbitrarily restrained stiffened plate under moving loads. Int. J. Mech. Sci. 200, 106414 (2021)

    Article  Google Scholar 

  26. Frýba, L.: Vibration of Solids and Structures under MOVING Loads. 1999, Prague: Thomas Telford

  27. Esen, İ: A new finite element for transverse vibration of rectangular thin plates under a moving mass. Finite Elem. Anal. Des. 66, 26–35 (2013)

    Article  MathSciNet  Google Scholar 

  28. Esen, İ: A new FEM procedure for transverse and longitudinal vibration analysis of thin rectangular plates subjected to a variable velocity moving load along an arbitrary trajectory. Latin Am. J. Solids Struct. 12, 808–830 (2015)

    Article  Google Scholar 

  29. Chung, N.T., Hong, N.T., Thuy, L.X.: Dynamic analysis of cracked plate subjected to moving oscillator by finite element method. Math. Probl. Eng. 20, 19 (2019)

    MathSciNet  Google Scholar 

  30. Chen, J.-S., Chen, S.-Y., Hsu, W.-Z.: Effects of geometric nonlinearity on the response of a long beam on viscoelastic foundation to a moving mass. J. Sound Vib. 497, 115961 (2021)

    Article  Google Scholar 

  31. Banhart, J.: Manufacture, characterisation and application of cellular metals and metal foams. Prog. Mater Sci. 46(6), 559–632 (2001)

    Article  Google Scholar 

  32. Babaei, M., Kiarasi, F., Asemi, K., Hosseini, M.: Functionally graded saturated porous structures: a review. J. Comput. Appl. Mech. 53(2), 297–308 (2022)

    Google Scholar 

  33. Akbaş, ŞD., Dastjerdi, S., Akgöz, B., Civalek, Ö.: Dynamic analysis of functionally graded porous microbeams under moving load. Transp. Porous Media 2, 1–19 (2021)

    Google Scholar 

  34. Chen, D., Yang, J., Kitipornchai, S.: Free and forced vibrations of shear deformable functionally graded porous beams. Int. J. Mech. Sci. 108–109, 14–22 (2016)

    Article  Google Scholar 

  35. Wang, Y., Zhou, A., Fu, T., Zhang, W.: Transient response of a sandwich beam with functionally graded porous core traversed by a non-uniformly distributed moving mass. Int. J. Mech. Mater. Des. 16(3), 519–540 (2020)

    Article  Google Scholar 

  36. Nguyen, V.-L., Tran, M.-T., Chu, T.-B., Nguyen, T.-A., Nguyen, V.-L.: Nonlinear dynamic response of functionally graded porous beams under a moving mass using Reddy’s beam theory. Iran. J. Sci. Technol. Trans. Mech. Eng. 2, 52 (2023). https://doi.org/10.1007/s40997-023-00705-2

    Article  Google Scholar 

  37. Tian, Y., Li, Q., Feng, Y., Yu, Y., Wu, D., Chen, X., Gao, W.: Nonlinear dynamic analysis of the functionally graded graphene platelets reinforced porous plate under moving mass. Thin-Walled Struct. 183, 110363 (2023)

    Article  Google Scholar 

  38. Kiani, Y., Akbarzadeh, A.H., Chen, Z.T., Eslami, M.R.: Static and dynamic analysis of an FGM doubly curved panel resting on the Pasternak-type elastic foundation. Compos. Struct. 94(8), 2474–2484 (2012)

    Article  Google Scholar 

  39. Sofiyev, A.H.: Review of research on the vibration and buckling of the FGM conical shells. Compos. Struct. 211, 301–317 (2019)

    Article  Google Scholar 

  40. Van Long, N., Nguyen, V.-L., Tran, M.-T., Thai, D.-K.: Exact solution for nonlinear static behaviors of functionally graded beams with porosities resting on elastic foundation using neutral surface concept. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 236(1), 481–495 (2022)

    Article  Google Scholar 

  41. Nguyen, V.-L., Tran, M.-T., Nguyen, V.-L., Le, Q.-H.: Static behaviour of functionally graded plates resting on elastic foundations using neutral surface concept. Arch. Mech. Eng. 68(1), 5–22 (2021)

    Google Scholar 

  42. Dang, X.-H., Nguyen, V.-L., Tran, M.-T., Tran, B.-D., Nguyen, V.-L.: Nonlinear dynamic analysis of auxetic-FGM sandwich plates resting on a Kerr elastic substrate under blast loading. Proc. Inst. Mech. Eng. Part C 2, 63 (2024)

    Google Scholar 

  43. Kerr, A.D.: Elastic and viscoelastic foundation models. J. Appl. Mech. 31(3), 491–498 (1964)

    Article  Google Scholar 

  44. Haciyev, V., Sofiyev, A., Kuruoglu, N.: Free bending vibration analysis of thin bidirectionally exponentially graded orthotropic rectangular plates resting on two-parameter elastic foundations. Compos. Struct. 184, 372–377 (2018)

    Article  Google Scholar 

  45. Haciyev, V., Sofiyev, A.H., Kuruoglu, N.: On the free vibration of orthotropic and inhomogeneous with spatial coordinates plates resting on the inhomogeneous viscoelastic foundation. Mech. Adv. Mater. Struct. 26(10), 886–897 (2019)

    Article  Google Scholar 

  46. Sofiyev, A.H., Zerin, Z., Kuruoglu, N.: Dynamic behavior of FGM viscoelastic plates resting on elastic foundations. Acta Mech. 231, 1–17 (2020)

    Article  MathSciNet  Google Scholar 

  47. Sofiyev, A.: On the solution of dynamic stability problem of functionally graded viscoelastic plates with different initial conditions in viscoelastic media. Mathematics 11(4), 823 (2023)

    Article  Google Scholar 

  48. Ipek, C., Sofiyev, A., Fantuzzi, N., Efendiyeva, S.P.: Buckling behavior of nanocomposite plates with functionally graded properties under compressive loads in elastic and thermal environments. J. Appl. Comput. Mech. 9(4), 974–986 (2023)

    Google Scholar 

  49. Avey, M., Kadioglu, F., Ahmetolan, S., Fantuzzi, N.: Mathematical modeling and solution of nonlinear vibration problem of laminated plates with CNT originating layers interacting with two-parameter elastic foundation. J. Braz. Soc. Mech. Sci. Eng. 45(3), 185 (2023)

    Article  Google Scholar 

  50. Avey, M., Fantuzzi, N., Sofiyev, A.H., Kuruoglu, N.: Influences of elastic foundations on the nonlinear free vibration of composite shells containing carbon nanotubes within shear deformation theory. Compos. Struct. 286, 115288 (2022)

    Article  Google Scholar 

  51. Reddy, J.N.: Mechanics of Laminated Composite Plates and Shells: Theory and Analysis. CRC Press, New York (2003)

    Book  Google Scholar 

  52. Qatu, M.S.: Vibration of Laminated Shells and Plates. Academic Press, UK (2004)

    Google Scholar 

  53. Thai, H.T., Kim, S.E.: A review of theories for the modeling and analysis of functionally graded plates and shells. Compos. Struct. 128, 70–86 (2015)

    Article  Google Scholar 

  54. Krommer, M., Irschik, H.: Post-buckling of piezoelectric thin plates. Int. J. Struct. Stab. Dyn. 15(07), 1540020 (2015)

    Article  MathSciNet  Google Scholar 

  55. Zhang, Q., Li, S., Zhang, A.M., Peng, Y.: On nonlocal geometrically exact shell theory and modeling fracture in shell structures. Comput. Methods Appl. Mech. Eng. 386, 114074 (2021)

    Article  MathSciNet  Google Scholar 

  56. Xue, B., Zhang, A.M., Peng, Y.-X., Zhang, Q., Li, S.: A meshfree orthotropic laminated shell model for geometrically nonlinear static and dynamic analysis. Comput. Mech. 2, 63 (2023)

    Google Scholar 

  57. Avey, M., Kadioglu, F.: On the primary resonance of laminated moderately-thick plates containing of heterogeneous nanocomposite layers considering nonlinearity. Compos. Struct. 322, 117377 (2023)

    Article  Google Scholar 

  58. Orakdöğen, E., Küçükarslan, S., Sofiyev, A., Omurtag, M.: Finite element analysis of functionally graded plates for coupling effect of extension and bending. Meccanica 45, 63–72 (2010)

    Article  Google Scholar 

  59. Nguyen, V.-L., Tran, M.-T., Limkatanyu, S., Mohammad-Sedighi, H., Rungamornrat, J.: Reddy’s third-order shear deformation shell theory for free vibration analysis of rotating stiffened advanced nanocomposite toroidal shell segments in thermal environments. Acta Mech. 233(11), 4659–4684 (2022)

    Article  MathSciNet  Google Scholar 

  60. Dang, X.-H., Nguyen, V.-L., Tran, M.-T.: B-P Nguyen Thi, Free vibration characteristics of rotating functionally graded porous circular cylindrical shells with different boundary conditions. Iran. J. Sci. Technol. Trans. Mech. Eng. 46(1), 167–183 (2022)

    Article  Google Scholar 

  61. Reddy, J.N.: A Simple Higher-Order Theory for Laminated Composite Plates. (1984).

  62. Detournay, E., Cheng, A.H.D.: Fundamentals of Poroelasticity. In: Fairhurst, C. (ed.) Analysis and Design Methods, pp. 113–171. Pergamon, Oxford (1993)

    Chapter  Google Scholar 

  63. Tru, V.N., Long, N.V., Tu, T.M., Trang, V.T.T.: Static analysis of functionally graded saturated porous plate rested on pasternak elastic foundation by using a new quasi-3D higher-order shear deformation theory. Arch. Appl. Mech. 2, 63 (2023)

    Google Scholar 

  64. Rad, E.S., Saidi, A., Rezaei, A., Askari, M.: Shear deformation theories for elastic buckling of fluid-infiltrated porous plates: an analytical approach. Compos. Struct. 254, 112829 (2020)

    Article  Google Scholar 

  65. Thai, H.-T., Choi, D.-H.: A refined plate theory for functionally graded plates resting on elastic foundation. Compos. Sci. Technol. 71(16), 1850–1858 (2011)

    Article  Google Scholar 

  66. Şimşek, M.: Vibration analysis of a functionally graded beam under a moving mass by using different beam theories. Compos. Struct. 92(4), 904–917 (2010)

    Article  Google Scholar 

  67. Wang, Y., **e, K., Fu, T., Shi, C.: Vibration response of a functionally graded graphene nanoplatelet reinforced composite beam under two successive moving masses. Compos. Struct. 209, 928–939 (2019)

    Article  Google Scholar 

  68. Wu, L.H., Lu, Y.: Free vibration analysis of rectangular plates with internal columns and uniform elastic edge supports by pb-2 Ritz method. Int. J. Mech. Sci. 53(7), 494–504 (2011)

    Article  Google Scholar 

  69. Rezaei, A.S., Saidi, A.R.: Application of Carrera Unified Formulation to study the effect of porosity on natural frequencies of thick porous–cellular plates. Compos. B Eng. 91, 361–370 (2016)

    Article  Google Scholar 

  70. Thai, H.-T., Choi, D.-H.: Finite element formulation of various four unknown shear deformation theories for functionally graded plates. Finite Elem. Anal. Des. 75, 50–61 (2013)

    Article  MathSciNet  Google Scholar 

  71. Thang, P.T., Nguyen-Thoi, T., Lee, D., Kang, J., Lee, J.: Elastic buckling and free vibration analyses of porous-cellular plates with uniform and non-uniform porosity distributions. Aerosp. Sci. Technol. 79, 278–287 (2018)

    Article  Google Scholar 

  72. Ebrahimi, F., Habibi, S.: Deflection and vibration analysis of higher-order shear deformable compositionally graded porous plate. Steel Compos. Struct. 20(1), 205–225 (2016)

    Article  Google Scholar 

  73. Song, Q., Shi, J., Liu, Z., Wan, Y.: Dynamic analysis of rectangular thin plates of arbitrary boundary conditions under moving loads. Int. J. Mech. Sci. 117, 16–29 (2016)

    Article  Google Scholar 

  74. Wu, J.-J.: Vibration analyses of an inclined flat plate subjected to moving loads. J. Sound Vib. 299(1–2), 373–387 (2007)

    Article  Google Scholar 

Download references

Acknowledgements

This research is funded by Ministry of Education and Training under grand number B2023-XDA-10.

Funding

Funding for this research was provided by: Ministry of Education and Training (B2023-XDA-10).

Author information

Authors and Affiliations

  1. Department of Strength of Materials, Faculty of Building and Industrial Construction, Hanoi University of Civil Engineering, 55 Giai Phong Road, Hanoi, Vietnam

    Van-Long Nguyen, Van-Loi Nguyen & Minh-Tu Tran

  2. Department of Civil Engineering, Vinh University, 182 Le Duan, Vinh City, Vietnam

    Tuan-Anh Nguyen

Authors
  1. Van-Long Nguyen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Van-Loi Nguyen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tuan-Anh Nguyen
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Minh-Tu Tran
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Van-Loi Nguyen.

Ethics declarations

Conflict of interest

The authors have no relevant financial or non-financial interests to disclose.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

Matrices \({\varvec{K}}\), \({\varvec{M}}\), \({\varvec{F}}\), \({\varvec{R}}\), \(\overline{\user2{H}}\), and \({\varvec{S}}\) in Eq. (36) are given as follows:

$$\begin{aligned} & {\varvec{K}} = \left[ {\begin{array}{*{20}c} {{\varvec{K}}^{uu} } & {{\varvec{K}}^{uv} } & {{\varvec{K}}^{uw} } & {{\varvec{K}}^{ux} } & {{\varvec{K}}^{uy} } \\ {{\varvec{K}}^{vu} } & {{\varvec{K}}^{vv} } & {{\varvec{K}}^{vw} } & {{\varvec{K}}^{vx} } & {{\varvec{K}}^{vy} } \\ {{\varvec{K}}^{wu} } & {{\varvec{K}}^{wv} } & {{\varvec{K}}^{ww} } & {{\varvec{K}}^{wx} } & {{\varvec{K}}^{wy} } \\ {{\varvec{K}}^{xu} } & {{\varvec{K}}^{xv} } & {{\varvec{K}}^{xw} } & {{\varvec{K}}^{xx} } & {{\varvec{K}}^{xy} } \\ {{\varvec{K}}^{yu} } & {{\varvec{K}}^{yv} } & {{\varvec{K}}^{yw} } & {{\varvec{K}}^{yx} } & {{\varvec{K}}^{yy} } \\ \end{array} } \right];\;{\varvec{M}} = \left[ {\begin{array}{*{20}c} {{\varvec{M}}^{uu} } & {\varvec{0}} & {{\varvec{M}}^{uw} } & {{\varvec{M}}^{ux} } & {\varvec{0}} \\ {\varvec{0}} & {{\varvec{M}}^{vv} } & {{\varvec{M}}^{vw} } & {\varvec{0}} & {{\varvec{M}}^{vy} } \\ {{\varvec{M}}^{wu} } & {{\varvec{M}}^{wv} } & {{\varvec{M}}^{ww} } & {{\varvec{M}}^{wx} } & {{\varvec{M}}^{wy} } \\ {{\varvec{M}}^{xu} } & {\varvec{0}} & {{\varvec{M}}^{xw} } & {{\varvec{M}}^{xx} } & {\varvec{0}} \\ {\varvec{0}} & {{\varvec{M}}^{yv} } & {{\varvec{M}}^{yw} } & {\varvec{0}} & {{\varvec{M}}^{yy} } \\ \end{array} } \right]; \\ & {\varvec{F}} = \left\{ {\begin{array}{*{20}c} {\varvec{0}} \\ {\varvec{0}} \\ {{\varvec{F}}^{w} } \\ {\varvec{0}} \\ {\varvec{0}} \\ \end{array} } \right\}; \\ \end{aligned}$$
$$\begin{aligned} & {\varvec{R}} = \left[ {\begin{array}{*{20}c} {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {\varvec{0}} & {{\varvec{R}}^{ww} } & {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} \\ \end{array} } \right];\;\overline{\user2{H}} = \left[ {\begin{array}{*{20}c} {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {\varvec{0}} & {\overline{\user2{H}}^{ww} } & {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} \\ \end{array} } \right]; \\ & {\varvec{S}} = \left[ {\begin{array}{*{20}c} {{\varvec{S}}^{uu} } & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {{\varvec{S}}^{vv} } & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {\varvec{0}} & {{\varvec{S}}^{ww} } & {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} \\ \end{array} } \right]; \\ \end{aligned}$$

where entire elements of matrices \({\varvec{K}}\), \({\varvec{M}}\), \({\varvec{R}}\), \(\overline{\user2{H}}\), \({\varvec{S}}\) and \({\varvec{F}}\) are determined by:

$${\varvec{K}}^{uu} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {A_{11} \frac{4}{{a^{2} }}\frac{{\partial {\varvec{U}}}}{\partial \xi }\frac{{\partial {\varvec{U}}^{T} }}{\partial \xi } + A_{66} \frac{4}{{b^{2} }}\frac{{\partial {\varvec{U}}}}{\partial \eta }\frac{{\partial {\varvec{U}}^{T} }}{\partial \eta }} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{vv} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {A_{66} \frac{4}{{a^{2} }}\frac{{\partial {\varvec{V}}}}{\partial \xi }\frac{{\partial {\varvec{V}}^{T} }}{\partial \xi } + A_{22} \frac{4}{{b^{2} }}\frac{{\partial {\varvec{V}}}}{\partial \eta }\frac{{\partial {\varvec{V}}^{T} }}{\partial \eta }} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{ww} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ \begin{gathered} \kappa^{2} G_{11} \frac{16}{{a^{4} }}\frac{{\partial^{2} {\varvec{W}}}}{{\partial \xi^{2} }}\frac{{\partial^{2} {\varvec{W}}^{T} }}{{\partial \xi^{2} }} + 2\kappa^{2} G_{12} \frac{16}{{a^{2} b^{2} }}\frac{{\partial^{2} {\varvec{W}}}}{{\partial \xi^{2} }}\frac{{\partial^{2} {\varvec{W}}^{T} }}{{\partial \eta^{2} }} \hfill \\ + \kappa^{2} G_{22} \frac{16}{{b^{4} }}\frac{{\partial^{2} {\varvec{W}}}}{{\partial \eta^{2} }}\frac{{\partial^{2} {\varvec{W}}^{T} }}{{\partial \eta^{2} }} + 4\kappa^{2} G_{66} \frac{16}{{a^{2} b^{2} }}\frac{{\partial^{2} {\varvec{W}}}}{\partial \xi \partial \eta }\frac{{\partial^{2} {\varvec{W}}^{T} }}{\partial \xi \partial \eta } \hfill \\ + A^{s} \left( {\frac{4}{{a^{2} }}\frac{{\partial {\varvec{W}}}}{\partial \xi }\frac{{\partial {\varvec{W}}^{T} }}{\partial \xi } + \frac{4}{{b^{2} }}\frac{{\partial {\varvec{W}}}}{\partial \eta }\frac{{\partial {\varvec{W}}^{T} }}{\partial \eta }} \right) \hfill \\ + k_{w} {\varvec{WW}}^{T} + k_{sx} \frac{4}{{a^{2} }}\frac{{\partial {\varvec{W}}}}{\partial \xi }\frac{{\partial {\varvec{W}}^{T} }}{\partial \xi } + k_{sy} \frac{4}{{b^{2} }}\frac{{\partial {\varvec{W}}}}{\partial \eta }\frac{{\partial {\varvec{W}}^{T} }}{\partial \eta } \hfill \\ \end{gathered} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{xx} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {C_{11}^{*} \frac{4}{{a^{2} }}\frac{{\partial \user2{\varphi }}}{\partial \xi }\frac{{\partial \user2{\varphi }^{T} }}{\partial \xi } + C_{66}^{*} \frac{4}{{b^{2} }}\frac{{\partial \user2{\varphi }}}{\partial \eta }\frac{{\partial \user2{\varphi }^{T} }}{\partial \eta } + A^{s} \user2{\varphi \varphi }^{T} } \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{yy} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {C_{66}^{*} \frac{4}{{a^{2} }}\frac{{\partial {\varvec{\psi}}}}{\partial \xi }\frac{{\partial {\varvec{\psi}}^{T} }}{\partial \xi } + C_{22}^{*} \frac{4}{{b^{2} }}\frac{{\partial {\varvec{\psi}}}}{\partial \eta }\frac{{\partial {\varvec{\psi}}^{T} }}{\partial \eta } + A^{s} \user2{\psi \psi }^{T} } \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{uv} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {A_{12} \frac{4}{ab}\frac{{\partial {\varvec{U}}}}{\partial \xi }\frac{{\partial {\varvec{V}}^{T} }}{\partial \eta } + A_{66} \frac{4}{ab}\frac{{\partial {\varvec{U}}}}{\partial \eta }\frac{{\partial {\varvec{V}}^{T} }}{\partial \xi }} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{vu} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {A_{12} \frac{4}{ab}\frac{{\partial {\varvec{V}}}}{\partial \eta }\frac{{\partial {\varvec{U}}^{T} }}{\partial \xi } + A_{66} \frac{4}{ab}\frac{{\partial {\varvec{V}}}}{\partial \xi }\frac{{\partial {\varvec{U}}^{T} }}{\partial \eta }} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{uw} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ \begin{gathered} - \kappa D_{11} \frac{8}{{a^{3} }}\frac{{\partial {\varvec{U}}}}{\partial \xi }\frac{{\partial^{2} {\varvec{W}}^{T} }}{{\partial \xi^{2} }} - \kappa D_{12} \frac{8}{{ab^{2} }}\frac{{\partial {\varvec{U}}}}{\partial \xi }\frac{{\partial^{2} {\varvec{W}}^{T} }}{{\partial \eta^{2} }} \hfill \\ - 2\kappa D_{66} \frac{8}{{ab^{2} }}\frac{{\partial {\varvec{U}}}}{\partial \eta }\frac{{\partial^{2} {\varvec{W}}^{T} }}{\partial \xi \partial \eta } \hfill \\ \end{gathered} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{wu} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ \begin{gathered} - \kappa D_{11} \frac{8}{{a^{3} }}\frac{{\partial^{2} {\varvec{W}}}}{{\partial \xi^{2} }}\frac{{\partial {\varvec{U}}^{T} }}{\partial \xi } - \kappa D_{12} \frac{8}{{ab^{2} }}\frac{{\partial^{2} {\varvec{W}}}}{{\partial \eta^{2} }}\frac{{\partial {\varvec{U}}^{T} }}{\partial \xi } \hfill \\ - 2\kappa D_{66} \frac{8}{{ab^{2} }}\frac{{\partial^{2} {\varvec{W}}}}{\partial \xi \partial \eta }\frac{{\partial {\varvec{U}}^{T} }}{\partial \eta } \hfill \\ \end{gathered} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{vw} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ \begin{gathered} - \kappa D_{12} \frac{8}{{a^{2} b}}\frac{{\partial {\varvec{V}}}}{\partial \eta }\frac{{\partial^{2} {\varvec{W}}^{T} }}{{\partial \xi^{2} }} - \kappa D_{22} \frac{8}{{b^{3} }}\frac{{\partial {\varvec{V}}}}{\partial \eta }\frac{{\partial^{2} {\varvec{W}}^{T} }}{{\partial \eta^{2} }} \hfill \\ - 2\kappa D_{66} \frac{8}{{a^{2} b}}\frac{{\partial {\varvec{V}}}}{\partial \xi }\frac{{\partial^{2} {\varvec{W}}^{T} }}{\partial \xi \partial \eta } \hfill \\ \end{gathered} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{wv} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ \begin{gathered} - \kappa D_{12} \frac{8}{{a^{2} b}}\frac{{\partial^{2} {\varvec{W}}}}{{\partial \xi^{2} }}\frac{{\partial {\varvec{V}}^{T} }}{\partial \eta } - \kappa D_{22} \frac{8}{{b^{3} }}\frac{{\partial^{2} {\varvec{W}}}}{{\partial \eta^{2} }}\frac{{\partial {\varvec{V}}^{T} }}{\partial \eta } \hfill \\ - 2\kappa D_{66} \frac{8}{{a^{2} b}}\frac{{\partial^{2} {\varvec{W}}}}{\partial \xi \partial \eta }\frac{{\partial {\varvec{V}}^{T} }}{\partial \xi } \hfill \\ \end{gathered} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{ux} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {B_{11}^{*} \frac{4}{{a^{2} }}\frac{{\partial {\varvec{U}}}}{\partial \xi }\frac{{\partial \user2{\varphi }^{T} }}{\partial \xi } + B_{66}^{*} \frac{4}{{b^{2} }}\frac{{\partial {\varvec{U}}}}{\partial \eta }\frac{{\partial \user2{\varphi }^{T} }}{\partial \eta }} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{xu} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {B_{11}^{*} \frac{4}{{a^{2} }}\frac{{\partial \user2{\varphi }}}{\partial \xi }\frac{{\partial {\varvec{U}}^{T} }}{\partial \xi } + B_{66}^{*} \frac{4}{{b^{2} }}\frac{{\partial \user2{\varphi }}}{\partial \eta }\frac{{\partial {\varvec{U}}^{T} }}{\partial \eta }} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{uy} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {B_{12}^{*} \frac{4}{ab}\frac{{\partial {\varvec{U}}}}{\partial \xi }\frac{{\partial {\varvec{\psi}}^{T} }}{\partial \eta } + B_{66}^{*} \frac{4}{ab}\frac{{\partial {\varvec{U}}}}{\partial \eta }\frac{{\partial {\varvec{\psi}}^{T} }}{\partial \xi }} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{yu} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {B_{12}^{*} \frac{4}{ab}\frac{{\partial {\varvec{\psi}}}}{\partial \eta }\frac{{\partial {\varvec{U}}^{T} }}{\partial \xi } + B_{66}^{*} \frac{4}{ab}\frac{{\partial {\varvec{\psi}}}}{\partial \xi }\frac{{\partial {\varvec{U}}^{T} }}{\partial \eta }} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{vx} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {B_{12}^{*} \frac{4}{ab}\frac{{\partial {\varvec{V}}}}{\partial \eta }\frac{{\partial \user2{\varphi }^{T} }}{\partial \xi } + B_{66}^{*} \frac{4}{ab}\frac{{\partial {\varvec{V}}}}{\partial \xi }\frac{{\partial \user2{\varphi }^{T} }}{\partial \eta }} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{xv} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {B_{12}^{*} \frac{4}{ab}\frac{{\partial \user2{\varphi }}}{\partial \xi }\frac{{\partial {\varvec{V}}^{T} }}{\partial \eta } + B_{66}^{*} \frac{4}{ab}\frac{{\partial \user2{\varphi }}}{\partial \eta }\frac{{\partial {\varvec{V}}^{T} }}{\partial \xi }} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{vy} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {B_{22}^{*} \frac{4}{{b^{2} }}\frac{{\partial {\varvec{V}}}}{\partial \eta }\frac{{\partial {\varvec{\psi}}^{T} }}{\partial \eta } + B_{66}^{*} \frac{4}{{a^{2} }}\frac{{\partial {\varvec{V}}}}{\partial \xi }\frac{{\partial {\varvec{\psi}}^{T} }}{\partial \xi }} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{yv} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {B_{22}^{*} \frac{4}{{b^{2} }}\frac{{\partial {\varvec{\psi}}}}{\partial \eta }\frac{{\partial {\varvec{V}}^{T} }}{\partial \eta } + B_{66}^{*} \frac{4}{{a^{2} }}\frac{{\partial {\varvec{\psi}}}}{\partial \xi }\frac{{\partial {\varvec{V}}^{T} }}{\partial \xi }} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{wx} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ \begin{gathered} E_{11}^{*} \frac{8}{{a^{3} }}\frac{{\partial^{2} {\varvec{W}}}}{{\partial \xi^{2} }}\frac{{\partial \user2{\varphi }^{T} }}{\partial \xi } + E_{12}^{*} \frac{8}{{ab^{2} }}\frac{{\partial^{2} {\varvec{W}}}}{{\partial \eta^{2} }}\frac{{\partial \user2{\varphi }^{T} }}{\partial \xi } \hfill \\ + 2E_{66}^{*} \frac{8}{{ab^{2} }}\frac{{\partial^{2} {\varvec{W}}}}{\partial \xi \partial \eta }\frac{{\partial \user2{\varphi }^{T} }}{\partial \eta } + A^{s} \frac{2}{a}\frac{{\partial {\varvec{W}}}}{\partial \xi }\user2{\varphi }^{T} \hfill \\ \end{gathered} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{xw} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ \begin{gathered} E_{11}^{*} \frac{8}{{a^{3} }}\frac{{\partial \user2{\varphi }}}{\partial \xi }\frac{{\partial^{2} {\varvec{W}}^{T} }}{{\partial \xi^{2} }} + E_{12}^{*} \frac{8}{{ab^{2} }}\frac{{\partial \user2{\varphi }}}{\partial \xi }\frac{{\partial^{2} {\varvec{W}}^{T} }}{{\partial \eta^{2} }} \hfill \\ + 2E_{66}^{*} \frac{8}{{ab^{2} }}\frac{{\partial \user2{\varphi }}}{\partial \eta }\frac{{\partial^{2} {\varvec{W}}^{T} }}{\partial \xi \partial \eta } + A^{s} \frac{2}{a}\user2{\varphi }\frac{{\partial {\varvec{W}}^{T} }}{\partial \xi } \hfill \\ \end{gathered} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{wy} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ \begin{gathered} E_{12}^{*} \frac{8}{{a^{2} b}}\frac{{\partial^{2} {\varvec{W}}}}{{\partial \xi^{2} }}\frac{{\partial {\varvec{\psi}}^{T} }}{\partial \eta } + E_{22}^{*} \frac{8}{{b^{3} }}\frac{{\partial^{2} {\varvec{W}}}}{{\partial \eta^{2} }}\frac{{\partial {\varvec{\psi}}^{T} }}{\partial \eta } \hfill \\ + 2E_{66}^{*} \frac{8}{{a^{2} b}}\frac{{\partial^{2} {\varvec{W}}}}{\partial \xi \partial \eta }\frac{{\partial {\varvec{\psi}}^{T} }}{\partial \xi } + A^{s} \frac{2}{b}\frac{{\partial {\varvec{W}}}}{\partial \eta }{\varvec{\psi}}^{T} \hfill \\ \end{gathered} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{yw} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ \begin{gathered} E_{12}^{*} \frac{8}{{a^{2} b}}\frac{{\partial {\varvec{\psi}}}}{\partial \eta }\frac{{\partial^{2} {\varvec{W}}^{T} }}{{\partial \xi^{2} }} + E_{22}^{*} \frac{8}{{b^{3} }}\frac{{\partial {\varvec{\psi}}}}{\partial \eta }\frac{{\partial^{2} {\varvec{W}}^{T} }}{{\partial \eta^{2} }} \hfill \\ + 2E_{66}^{*} \frac{8}{{a^{2} b}}\frac{{\partial {\varvec{\psi}}}}{\partial \xi }\frac{{\partial^{2} {\varvec{W}}^{T} }}{\partial \xi \partial \eta } + A^{s} \frac{2}{b}{\varvec{\psi}}\frac{{\partial {\varvec{W}}^{T} }}{\partial \eta } \hfill \\ \end{gathered} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{xy} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {C_{12}^{*} \frac{4}{ab}\frac{{\partial \user2{\varphi }}}{\partial \xi }\frac{{\partial {\varvec{\psi}}^{T} }}{\partial \eta } + C_{66}^{*} \frac{4}{ab}\frac{{\partial \user2{\varphi }}}{\partial \eta }\frac{{\partial {\varvec{\psi}}^{T} }}{\partial \xi }} \right]d\xi d\eta } } ;$$
$${\varvec{K}}^{yx} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {C_{12}^{*} \frac{4}{ab}\frac{{\partial {\varvec{\psi}}}}{\partial \eta }\frac{{\partial \user2{\varphi }^{T} }}{\partial \xi } + C_{66}^{*} \frac{4}{ab}\frac{{\partial {\varvec{\psi}}}}{\partial \xi }\frac{{\partial \user2{\varphi }^{T} }}{\partial \eta }} \right]d\xi d\eta } } ;$$
$${\varvec{M}}^{uu} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {I_{0} {\varvec{UU}}^{T} } \right]d\xi d\eta } } ;\;M^{vv} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {I_{0} {\varvec{VV}}^{T} } \right]d\xi d\eta } } ;$$
$${\varvec{M}}^{ww} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {I_{0} {\varvec{WW}}^{T} + \kappa^{2} I_{6} \left( {\frac{4}{{a^{2} }}\frac{{\partial {\varvec{W}}}}{\partial \xi }\frac{{\partial {\varvec{W}}^{T} }}{\partial \xi } + \frac{4}{{b^{2} }}\frac{{\partial {\varvec{W}}}}{\partial \eta }\frac{{\partial {\varvec{W}}^{T} }}{\partial \eta }} \right)} \right]d\xi d\eta } } ;$$
$${\varvec{M}}^{xx} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {K_{2} \user2{\varphi \varphi }^{T} } \right]d\xi d\eta } } ;\;{\varvec{M}}^{yy} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {K_{2} \user2{\psi \psi }^{T} } \right]d\xi d\eta } } ;$$
$${\varvec{M}}^{uw} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ { - \kappa I_{3} \frac{2}{a}{\varvec{U}}\frac{{\partial {\varvec{W}}^{T} }}{\partial \xi }} \right]d\xi d\eta } } ;\;{\varvec{M}}^{wu} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ { - \kappa I_{3} \frac{2}{a}\frac{{\partial {\varvec{W}}}}{\partial \xi }{\varvec{U}}^{T} } \right]d\xi d\eta } } ;$$
$${\varvec{M}}^{vw} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ { - \kappa I_{3} \frac{2}{b}{\varvec{V}}\frac{{\partial {\varvec{W}}^{T} }}{\partial \eta }} \right]d\xi d\eta } } ;\;{\varvec{M}}^{wv} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ { - \kappa I_{3} \frac{2}{b}\frac{{\partial {\varvec{W}}}}{\partial \eta }{\varvec{V}}^{T} } \right]d\xi d\eta } } ;$$
$${\varvec{M}}^{ux} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {J_{1} \user2{U\varphi }^{T} } \right]d\xi d\eta } } ;\;{\varvec{M}}^{xu} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {J_{1} \user2{\varphi U}^{T} } \right]d\xi d\eta } } ;$$
$${\varvec{M}}^{vy} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {J_{1} \user2{V\psi }^{T} } \right]d\xi d\eta } } ;\;{\varvec{M}}^{yv} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {J_{1} \user2{\psi V}^{T} } \right]d\xi d\eta } } ;$$
$${\varvec{M}}^{wx} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ { - \kappa J_{4} \frac{2}{a}\frac{{\partial {\varvec{W}}}}{\partial \xi }\user2{\varphi }^{T} } \right]d\xi d\eta } } ;\;{\varvec{M}}^{xw} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ { - \kappa J_{4} \frac{2}{a}\user2{\varphi }\frac{{\partial {\varvec{W}}^{T} }}{\partial \xi }} \right]d\xi d\eta } } ;$$
$${\varvec{M}}^{wy} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ { - \kappa J_{4} \frac{2}{b}\frac{{\partial {\varvec{W}}}}{\partial \eta }{\varvec{\psi}}^{T} } \right]d\xi d\eta } } ;\;{\varvec{M}}^{yw} = \frac{ab}{4}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ { - \kappa J_{4} \frac{2}{b}{\varvec{\psi}}\frac{{\partial {\varvec{W}}^{T} }}{\partial \eta }} \right]d\xi d\eta } } ;$$
$${\varvec{F}}^{w} = - c(t)Mg\left. {\varvec{W}} \right|_{{\xi = \xi_{M} ,\eta = \eta_{M} }} ;$$
$${\varvec{R}}^{ww} = c(t)\left[ {v_{x} v_{y} \frac{4}{ab}\frac{{\partial {\varvec{W}}}}{\partial \xi }\frac{{\partial {\varvec{W}}^{T} }}{\partial \eta } + v_{x}^{2} \frac{4}{{a^{2} }}\frac{{\partial {\varvec{W}}}}{\partial \xi }\frac{{\partial {\varvec{W}}^{T} }}{\partial \xi } + v_{y}^{2} \frac{4}{{b^{2} }}\frac{{\partial {\varvec{W}}}}{\partial \eta }\frac{{\partial W^{T} }}{\partial \eta }} \right]_{{\xi = \xi_{M} ,\eta = \eta_{M} }} ;$$
$${\varvec{S}}^{uu} = \left. {c(t){\varvec{UU}}^{T} } \right|_{{\xi = \xi_{M} ,\eta = \eta_{M} }} ;\;{\varvec{S}}^{vv} = \left. {c(t){\varvec{VV}}^{T} } \right|_{{\xi = \xi_{M} ,\eta = \eta_{M} }} ;\;{\varvec{S}}^{ww} = \left. {c(t){\varvec{WW}}^{T} } \right|_{{\xi = \xi_{M} ,\eta = \eta_{M} }} ;$$
$$\overline{\user2{H}}^{ww} = c(t)\left[ {v_{x} \frac{2}{a}{\varvec{W}}\frac{{\partial {\varvec{W}}^{T} }}{\partial \xi } + v_{y} \frac{2}{b}{\varvec{W}}\frac{{\partial {\varvec{W}}^{T} }}{\partial \eta }} \right]_{{\xi = \xi_{M} ,\eta = \eta_{M} }} ;$$

with \(\xi_{M} = \frac{{2x_{0} }}{a} - 1;\eta_{M} = \frac{{2y_{0} }}{b} - 1.\)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nguyen, VL., Nguyen, VL., Nguyen, TA. et al. Dynamic responses of saturated functionally graded porous plates resting on elastic foundation and subjected to a moving mass using pb2-Ritz method. Acta Mech (2024). https://doi.org/10.1007/s00707-024-03978-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00707-024-03978-z

Search

Navigation