A closed-form yield criterion for porous materials with Mises–Schleicher–Burzyński matrix containing cylindrical voids

Abstract

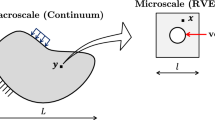
This work develops a closed-form yield criterion applicable to porous materials with pressure-dependent matrix presenting tension–compression asymmetry (Mises–Schleicher–Burzyński material) containing parallel cylindrical voids. To develop the strength criterion, the stress-based variational homogenization approach due to Cheng et al. (Int J Plast 55:133–151, 2014) is extended to the case of a hollow cylinder under generalized plane strain conditions subjected to axisymmetric loading. Adopting a strictly statically admissible trial stress field, the homogenization procedure results in an approximate yield locus depending on the current material porosity, tension–compression material asymmetry, the mean lateral stress, and an equivalent shear stress. The analytical criterion provides exact solutions for purely hydrostatic loading. Theoretical results are compared with finite element (FE) simulations considering cylindrical unit-cells with distinct porosity levels, different values of the tension–compression asymmetry, and a wide range of stress triaxialities. Based on comparisons, the theoretical results are found to be in good agreement with FE simulations for most of the loading conditions and material features considered in this study. More accurate theoretical predictions are provided when higher material porosities and/or lower tension–compression asymmetries are considered. Overall, the main outcome of this work is a closed-form yield function proving fairly accurate predictions to engineering applications, in which pressure-dependent and tension–compression asymmetric porous materials with cylindrical voids are dealt with. This can be the case of honeycomb structures or additively manufactured materials, in which metal matrix composites are employed.

Appendices

Appendix A: Development of the first stress field $\varvec{\sigma }_{1}$

To develop the first trial stress field $\varvec{\sigma }_{1}$, the analytical development presented by Monchiet and Kondo [30] is considered. They have proposed an exact solution for a plastic hollow sphere with a Mises–Schleicher [36] matrix material. For a plastic loading, the yield criterion has to satisfy the condition (see Eq. (3)):

$$\begin{aligned} \sigma _{e}^{2}+3\alpha \sigma _{0}\sigma _{h}-\sigma _{0}^{2}=0 \end{aligned}$$

(A.1)

where, for a cylindrically symmetric problem, the von Mises equivalent stress and the hydrostatic stress are given, respectively, by:

$$\begin{aligned} \sigma _{e}=\sqrt{\frac{3}{4}\left( \sigma _{\theta }-\sigma _{r}\right) ^{2}+\frac{9}{4}\left( \sigma _{z}-\sigma _{h}\right) ^{2}}\,\,\text { and }\,\,\sigma _{h}=\frac{1}{3}\left( \sigma _{r}+\sigma _{\theta }+\sigma _{z}\right), \end{aligned}$$

(A.2)

being $\sigma _{r}$, $\sigma _{\theta }$, and $\sigma _{z}$ the radial, circumferential, and longitudinal stresses. For the first trial stress field $\varvec{\sigma }_{1}$ it will be assumed that $\sigma _{z}=\sigma _{h}$, thus $\sigma _{e}$ and $\sigma _{h}$ become:

$$\begin{aligned} \sigma _{e}=\sqrt{\frac{3}{4}}\left( \sigma _{\theta }-\sigma _{r}\right) \epsilon \,\,\text { and }\,\,\sigma _{h}=\frac{1}{2}\left( \sigma _{r}+\sigma _{\theta }\right) \end{aligned}$$

(A.3.1,2)

where $\epsilon =\mathrm {sign}\left( \sigma _{\theta }-\sigma _{r}\right)$ is the sign of $\left( \sigma _{\theta }-\sigma _{r}\right)$. It is worth mentioning that, in addition to simplify the expression of the equivalent stress $\sigma _{e}$, assuming that $\sigma _{z}=\sigma _{h}$ results in a purely hydrostatic macroscopic stress field (see Eq. (28)).

Following the development of Monchiet and Kondo [30], a positive function $G\left( r\right)$, depending on the radial coordinate r, is introduced in a manner that:

$$\begin{aligned} \sigma _{e}=\sigma _{0}G\left( r\right). \end{aligned}$$

(A.4)

Therefore, using Eq. (A.1), the hydrostatic stress reads:

$$\begin{aligned} \sigma _{h}=\frac{\sigma _{0}}{3\alpha }\left[ 1-G^{2}\left( r\right) \right]. \end{aligned}$$

(A.5)

Moreover, combining Eqs. (A.3), (A.4), (A.5), the solution in terms of $\sigma _{r}$ and $\sigma _{\theta }$ results:

$$\begin{aligned}&\sigma _{r}=\frac{\sigma _{0}}{3\alpha }\left[ 1-G^{2}\left( r\right) \right] -\sqrt{\frac{1}{3}}\sigma _{0}G\left( r\right) \epsilon, \end{aligned}$$

(A.6)

$$\begin{aligned}&\sigma _{\theta }=\frac{\sigma _{0}}{3\alpha }\left[ 1-G^{2}\left( r\right) \right] +\sqrt{\frac{1}{3}}\sigma _{0}G\left( r\right) \epsilon. \end{aligned}$$

(A.7)

Introducing the last two equations into Eq. (9) yields:

$$\begin{aligned} G\left( r\right) \frac{\mathrm{d}G\left( r\right) }{\mathrm{d}r}+\frac{A}{2}\frac{dG\left( r\right) }{\mathrm{d}r}+\frac{A}{r}G\left( r\right) =0 \end{aligned}$$

(A.8)

where $A=\sqrt{3}\alpha \epsilon$. The solution of the differential equation (A.8) is:

$$\begin{aligned} G\left( r\right) =\frac{A}{2}W\left( \frac{2\exp \left( \frac{C_{1}}{A}\right) }{Ar^{2}}\right) \end{aligned}$$

or

$$\begin{aligned} G\left( r\right) =\frac{\sqrt{3}\alpha \epsilon }{2}W\left( p\frac{a^{2}}{r^{2}}\right) \end{aligned}$$

(A.9)

where $W\left( x\right)$ is the Lambert W function, which is the inverse of $x=W\exp \left( W\right)$. Function p is defined as:

$$\begin{aligned} p=\frac{2\exp \left( \frac{C_{1}}{\sqrt{3}\alpha \epsilon }\right) }{\sqrt{3}\alpha \epsilon a^{2}}. \end{aligned}$$

(A.10)

Thus, parameter p has both positive $\left( p_{+}\right)$ and negative $\left( p_{-}\right)$ branches:

$$\begin{aligned} p={\left\{ \begin{array}{ll} p_{+}=\frac{2\exp \left( \frac{C_{1}}{\sqrt{3}\alpha }\right) }{\sqrt{3}\alpha a^{2}}\\ p_{-}=-\frac{2\exp \left( -\frac{C_{1}}{\sqrt{3}\alpha }\right) }{\sqrt{3}\alpha a^{2}} \end{array}\right. }. \end{aligned}$$

(A.11)

Since $G\left( r\right) \ge 0$, from Eqs. (A.9) and (A.11), it is concluded that $\mathrm {sign}\left( W\right) =\mathrm {sign}\left( p\right)$ and thus $\epsilon =\mathrm {sign}\left( p\right)$.

Given the solution (A.9), the stress components become (see Eqs. (A.6) and (A.7)):

$$\begin{aligned}&\sigma _{r}=\frac{\sigma _{0}}{3\alpha }\left[ 1-\frac{3\alpha ^{2}}{4}W^{2}\left( p\frac{a^{2}}{r^{2}}\right) -\frac{3\alpha ^{2}}{2}W\left( p\frac{a^{2}}{r^{2}}\right) \right], \end{aligned}$$

(A.12)

$$\begin{aligned}&\sigma _{\theta }=\frac{\sigma _{0}}{3\alpha }\left[ 1-\frac{3\alpha ^{2}}{4}W^{2}\left( p\frac{a^{2}}{r^{2}}\right) +\frac{3\alpha ^{2}}{2}W\left( p\frac{a^{2}}{r^{2}}\right) \right]. \end{aligned}$$

(A.13)

From Eq. (A.3.2), the hydrostatic and axial stresses are then calculated:

$$\begin{aligned} \sigma _{h}=\sigma _{z}=\frac{\sigma _{0}}{3\alpha }\left[ 1-\frac{3\alpha ^{2}}{4}W^{2}\left( p\frac{a^{2}}{r^{2}}\right) \right] \end{aligned}$$

(A.14)

Coefficient p can be determined from the boundary condition $\sigma _{r}\left( r=a\right) =0$. Thus, from Eq. (A.12):

$$\begin{aligned} \alpha ^{2}W^{2}\left( p\right) +2\alpha ^{2}W\left( p\right) -\frac{4}{3}=0. \end{aligned}$$

(A.15)

The corresponding roots of the last equation are:

$$\begin{aligned} W\left( p\right) =\frac{-\alpha \pm \sqrt{\alpha ^{2}+\frac{4}{3}}}{\alpha }. \end{aligned}$$

Thus, both the positive $\left( p_{+}\right)$ and negative $\left( p_{-}\right)$ branches of p are determined:

$$\begin{aligned} {\left\{ \begin{array}{ll} p=p_{+}=z_{+}\exp \left( z_{+}\right) , &{} z_{+}=\frac{-\alpha +\sqrt{\alpha ^{2}+\frac{4}{3}}}{\alpha }\\ \mathrm {or}\\ p=p_{-}=z_{-}\exp \left( z_{-}\right) , &{} z_{-}=\frac{-\alpha -\sqrt{\alpha ^{2}+\frac{4}{3}}}{\alpha } \end{array}\right. } . \end{aligned}$$

(A.16)

Appendix B: Development of the second stress field $\varvec{\sigma }_{2}$

To develop the second trial stress field $\varvec{\sigma }_{2}$, a homogeneous longitudinal stress state is considered:

$$\begin{aligned} \varvec{\sigma }_{2}=\sigma _{z}\varvec{e}_{z}\otimes \varvec{e}_{z}. \end{aligned}$$

(B.1)

Since $\sigma _{z}$ is constant, the stress tensor $\varvec{\sigma }_{2}$ readily satisfies the equilibrium equation $\mathrm {div}\varvec{\sigma }_{2}=\varvec{0}$. For this particular stress tensor, the von Mises equivalent stress and the hydrostatic stress become, respectively:

$$\begin{aligned} \sigma _{e}=\sigma _{z}\mathrm {sign}\left( \sigma _{z}\right) \,\,\text { and }\,\,\sigma _{h}=\frac{1}{3}\sigma _{z}. \end{aligned}$$

(B.2)

Therefore, the yield condition yields (see Eq. (3)):

$$\begin{aligned} \sigma _{z}^{2}+\alpha \sigma _{0}\sigma _{z}-\sigma _{0}^{2}=0. \end{aligned}$$

(B.3)

Thus, solving the previous equation in terms of the longitudinal stress, we obtain:

$$\begin{aligned} \sigma _{z}=\left( -\alpha \pm \sqrt{\alpha ^{2}+4}\right) \frac{\sigma _{0}}{2}. \end{aligned}$$

(B.4)

Since $\sigma _{0}>0$, the term $\left( -\alpha \pm \sqrt{\alpha ^{2}+4}\right)$ defines the sign of the longitudinal stress $\sigma _{z}$. Notice in Eq. (B.4) that the solution depends on the tension–compression asymmetry by means of parameter $\alpha$ (or k, see Eq. (2)).

Appendix C: Development of the macroscopic yield function $\Phi \left( \varvec{\Sigma }\right)$

This Section is intended to present the development leading to the macroscopic yield function $\Phi \left( \varvec{\Sigma }\right)$. Starting from condition (19), having in mind the matrix yield function (3), the following relation is obtained:

$$\begin{aligned} \Phi \left( \varvec{\Sigma }\right) =\frac{1}{\left| \Omega \right| }\int _{a}^{b}\int _{-\frac{H}{2}}^{\frac{H}{2}}\int _{0}^{2\pi }\left( \sigma _{e}^{2}+3\alpha \sigma _{0}\sigma _{h}-\sigma _{0}^{2}\right) rd\theta \mathrm{d}z\mathrm{d}r. \end{aligned}$$

(C.1)

In view of the stress superposition (21) and the trial stress fields given in Eqs. (22)–(24) and (30), the first term on the right-hand side of Eq. (C.1) can be integrated as follows:

$$\begin{aligned} \frac{1}{\left| \Omega \right| }\int _{-\frac{H}{2}}^{\frac{H}{2}}\int _{0}^{2\pi }\int _{a}^{b}\sigma _{e}^{2}r\mathrm{d}r\mathrm{d}\theta \mathrm{d}z&=\frac{1}{\left| \Omega \right| }\int _{-\frac{H}{2}}^{\frac{H}{2}}\int _{0}^{2\pi }\int _{a}^{b}\left[ A_{1}^{2}\frac{3\alpha ^{2}}{4}W^{2}\left( p\frac{a^{2}}{r^{2}}\right) +\frac{9}{4}\left( \frac{2}{3}A_{2}\right) ^{2}\right] r\mathrm{d}r\mathrm{d}\theta \mathrm{d}z\nonumber \\&=-\left( f+\frac{3\alpha ^{2}}{4}\Upsilon \right) A_{1}^{2}+A_{2}^{2}\left( 1-f\right) \end{aligned}$$

(C.2)

in which relations $\left| \Omega \right| =H\pi b^{2}$, $f=\frac{a^{2}}{b^{2}}$ and condition (A.15) have been employed. Moreover, parameter $\Upsilon$ is calculated using Eq. (29).

Moreover, also using Eqs. (21), (22)–(24), and (30), the second term on the right-hand side of Eq. (C.1) is integrated:

$$\begin{aligned} \frac{3\alpha \sigma _{0}}{\left| \Omega \right| }\int _{-\frac{H}{2}}^{\frac{H}{2}}\int _{0}^{2\pi }\int _{a}^{b}\sigma _{h}r\mathrm{d}r\mathrm{d}\theta \mathrm{d}z&=\frac{2\pi H\sigma _{0}A_{1}}{\Omega }\int _{a}^{b}\left[ 1-\frac{3\alpha ^{2}}{4}W^{2}\left( p\frac{a^{2}}{r^{2}}\right) \right] r\mathrm{d}r+\frac{2\pi H\alpha \sigma _{0}A_{2}}{\Omega }\int _{a}^{b}rdr\nonumber \\&=\sigma _{0}\left( 1+\frac{3}{4}\alpha ^{2}\Upsilon \right) A_{1}+\left( 1-f\right) \alpha \sigma _{0}A_{2} \end{aligned}$$

(C.3)

where relations $\left| \Omega \right| =H\pi b^{2}$, $f=\frac{a^{2}}{b^{2}}$, and Eq. (A.15) have been used again.

Finally, the last term on the right hand side of Eq. (C.1) can be easily integrated:

$$\begin{aligned} \frac{1}{\left| \Omega \right| }\int _{-\frac{H}{2}}^{\frac{H}{2}}\int _{0}^{2\pi }\int _{a}^{b}\sigma _{0}^{2}rdrd\theta \mathrm{d}z=\left( 1-f\right) \sigma _{0}^{2}. \end{aligned}$$

(C.4)

Therefore, using Eqs. (C.2)–(C.4), Eq. (C.1) becomes:

$$\begin{aligned} \Phi \left( \varvec{\Sigma }\right) =-\left( f+\frac{3\alpha ^{2}}{4}\Upsilon \right) A_{1}^{2}+A_{2}^{2}\left( 1-f\right) +\sigma _{0}\left( 1+\frac{3}{4}\alpha ^{2}\Upsilon \right) A_{1}+\left( 1-f\right) \alpha \sigma _{0}A_{2}-\left( 1-f\right) \sigma _{0}^{2}=0. \end{aligned}$$

(C.5)

Appendix D: Reference criteria for porous materials with cylindrical voids

This Section aims at summarizing yield criteria that have been proposed in the literature to porous materials with cylindrical voids. Those criteria will be considered in this work for comparison purposes. The first one is the well-known Gurson [17] criterion:

$$\begin{aligned} \Phi _{G}=\frac{\Sigma _{e}^{2}}{\sigma _{0}^{2}}+2f\cosh \left( \frac{\sqrt{3}\Sigma _{m}}{\sigma _{0}}\right) -\left( 1+f^{2}\right) =0 \end{aligned}$$

(D.1)

where $\Sigma _{e}$ is the von Mises equivalent stress and $\Sigma _{m}=\nicefrac {\left( \Sigma _{1}+\Sigma _{2}\right) }{2}$ denotes the mean lateral stress. In the specific axisymmetric case of the cylinder shown in Fig. 1c, we have $\Sigma _{m}=\Sigma _{1}=\Sigma _{2}$ and $\Sigma _{e}=\left| \Sigma _{3}-\Sigma _{1}\right|$, that is, the von Mises equivalent stress has the absolute value of the equivalent shear stress $\Sigma _{sh}$ defined in Eq. (32). For a purely hydrostatic loading $\left( \Sigma _{e}=\Sigma _{sh}=0\right)$, Eq. (D.1) provides the well-known exact solution:

$$\begin{aligned} \left| \Sigma _{m}\right| =\frac{\sigma _{0}}{\sqrt{3}}\ln \left( f\right) \end{aligned}$$

(D.2)

where the identity $\mathrm {arcosh}\left( x\right) =\ln \left( x+\sqrt{x^{2}-1}\right)$, for $x\ge 1$, has been used. Notice that, for a purely hydrostatic case, we have $\Sigma _{m}=\Sigma _{h}$, being $\Sigma _{h}$ the hydrostatic stress.

The second one is the upper bound that has been developed by Lee and Oung [24] employing Gurson’s kinematic approach to porous materials with Mises–Schleicher matrix material:

$$\begin{aligned} \Phi _{LO}^{up}=\frac{\Sigma _{sh}^{2}}{\sigma _{0}^{2}}+3f\frac{\Sigma _{m}^{2}}{\sigma _{0}^{2}}+\alpha \left( 1-f\right) \frac{\left( 3\Sigma _{m}+\Sigma _{sh}\right) }{\sigma _{0}}-\left( 1-f\right) ^{2}=0 \end{aligned}$$

(D.3)

where relation $\Sigma _{e}=\pm \Sigma _{sh}$, between the equivalent von Mises stress $\Sigma _{e}$ and the equivalent shear stress $\Sigma _{sh}$ (see Eq. (32)), has been employed in order to have the same stress components as shown in Eq. (35). For a purely hydrostatic stress state $\left( \Sigma _{sh}=0\right)$, the previous criterion becomes:

$$\begin{aligned} 3f\frac{\Sigma _{m}^{2}}{\sigma _{0}^{2}}+3\alpha \left( 1-f\right) \frac{\Sigma _{m}}{\sigma _{0}}-\left( 1-f\right) ^{2}=0. \end{aligned}$$

(D.4)

In addition, when the special case with $\alpha \rightarrow 0$ is considered, it results in:

$$\begin{aligned} \left| \Sigma _{m}\right| =\frac{\sigma _{0}}{\sqrt{3}}\frac{\left( 1-f\right) }{\sqrt{f}} \end{aligned}$$

(D.5)

which differs from the exact solution (D.2). In order to recover Gurson’s model when $\alpha \rightarrow 0$ (von Mises matrix material) and also to provide better predictions for high triaxialities, the previous criterion (Eq. (D.3)) has been heuristically modified by Lee and Oung [24]. Their improved approximate criterion reads:

$$\begin{aligned} \Phi _{LO}^{app}=\frac{\Sigma _{sh}^{2}}{\sigma _{0}^{2}}+2f\cosh \left( \frac{\sqrt{3}\Sigma _{m}}{\sigma _{0}}\right) +\alpha \left( 1-f\right) \frac{\left( 3\Sigma _{m}+\Sigma _{sh}\right) }{\sigma _{0}}-\left( 1+f^{2}\right) =0 \end{aligned}$$

(D.6)

where relation $\Sigma _{e}=\pm \Sigma _{sh}$ has been used. Considering a purely hydrostatic loading $\left( \Sigma _{sh}=0\right)$, the improved criterion yields:

$$\begin{aligned} 2f\cosh \left( \frac{\sqrt{3}\Sigma _{m}}{\sigma _{0}}\right) +3\alpha \left( 1-f\right) \frac{\Sigma _{m}}{\sigma _{0}}-\left( 1+f^{2}\right) =0 \end{aligned}$$

(D.7)

which clearly recovers Eq. (D.2) when $\alpha \rightarrow 0$.