SpringerLink
Log in

Natural frequency veering and mode localization caused by straight through–cracks in rectangular plates with elastic boundary conditions

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

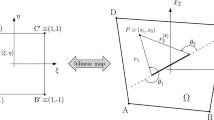
A solution method is presented for vibration analysis of through-cracked rectangular plates. A domain decomposition technique is employed in combination with a set of admissible functions which were previously proposed for triangular and rectangular plates with elastic boundary conditions. The continuity conditions at interconnecting boundaries of the subdomains are enforced by translational and rotational springs with zero or infinite stiffness. The Rayleigh–Ritz method is employed to determine the generalized coordinates and the corresponding modal frequencies and shapes. This special set of admissible functions allows all the involved integrals to be calculated analytically in closed form. Numerical examples are presented for plates with various crack configurations and boundary conditions. The current results are compared with those available in the literature to verify their convergence and correctness. The main advantage of the proposed method lies in its applicability to various combinations of boundary conditions and crack configurations. This method is then employed to determine the modal characteristics of simply supported square plates by focusing on the effects of various crack parameters on frequency veering, mode splitting, and mode localization. Finally, experiments are reported for three rectangular plates with different cracks for validation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price includes VAT (Germany)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Lynn, P.P., Kumbasar, N.: Free vibration of thin rectangular plates having narrow cracks with simply supported edges. Mech. Dev. 4, 911–928 (1967)

    Google Scholar 

  2. Stahl, B., Keer, L.M.: Vibration and stability of cracked rectangular plates. Int. J. Solids Struct. 8, 69–91 (1972)

    Article  Google Scholar 

  3. Hirano, Y., Okazaki, K.: Vibration of cracked rectangular plates. Bull. JSME 23, 732–740 (1980)

    Article  MathSciNet  Google Scholar 

  4. Aggarwala, B.D., Ariel, P.D.: Vibration and bending of a cracked plate. Rozprawy Inzynierskie 29, 295–310 (1981)

    MATH  Google Scholar 

  5. Solecki, R.: Bending vibration of a simply supported rectangular plate with a crack parallel to one edge. Eng. Fract. Mech. 18, 1111–1118 (1983)

    Article  Google Scholar 

  6. Solecki, R.: Bending vibration of a rectangular plate with arbitrarily located rectilinear crack. Eng. Fract. Mech. 22, 687–695 (1985)

    Article  Google Scholar 

  7. Khadem, S.E., Rezaee, M.: Introduction of modified comparison functions for vibration analysis of a rectangular cracked plate. J. Sound Vib. 236, 245–258 (2000)

    Article  Google Scholar 

  8. Yu, S.D.: Free flexural vibration of rectangular plates having single cracks. In: Proceedings of the 23rd International Congress of Aeronautical Sciences (ICAS), pp. 421–428 (2002)

  9. Yuan, J., Dickinson, S.M.: The flexural vibration of rectangular plate systems approached by using artificial springs in the Rayleigh–Ritz method. J. Sound Vib. 159, 39–55 (1992)

    Article  Google Scholar 

  10. Liew, K.M., Hung, K.C., Lim, M.K.: A solution method for analysis of cracked plates under vibration. Eng. Fract. Mech. 48, 393–404 (1994)

    Article  Google Scholar 

  11. Huang, C.S., Leissa, A.W.: Vibration analysis of rectangular plates with side cracks via the Ritz method. J. Sound Vib. 323, 974–988 (2009)

    Article  Google Scholar 

  12. Huang, C.S., Leissa, A.W., Chan, C.W.: Vibrations of rectangular plates with internal cracks or slits. Int. J. Mech. Sci. 53, 436–445 (2011)

    Article  Google Scholar 

  13. Huang, C.S., Lin, Y.J.: Fourier series solutions for vibrations of a rectangular plate with a straight through crack. Appl. Math. Model. 40, 10389–10403 (2016)

    Article  MathSciNet  Google Scholar 

  14. Li, W.L.: Vibration analysis of rectangular plates with general elastic boundary supports. J. Sound Vib. 273, 619–635 (2004)

    Article  Google Scholar 

  15. Eftekhari, S.A., Jafari, A.A.: A novel and accurate Ritz formulation for free vibration of rectangular and skew plates. J. Appl. Mech. 79, 64504 (2012)

    Article  Google Scholar 

  16. Eftekhari, S.A., Jafari, A.A.: A simple and accurate Ritz formulation for free vibration of thick rectangular and skew plates with general boundary conditions. Acta Mech. 224, 193–209 (2013)

    Article  MathSciNet  Google Scholar 

  17. Qian, G., Gu, S., Jiang, J.: A finite element model of cracked plates and application to vibration problems. Comput. Struct. 39, 483–487 (1991)

    Article  Google Scholar 

  18. Krawczuk, M.: Natural vibrations of rectangular plates with a through crack. Arch. Appl. Mech. 63, 491–504 (1993)

    MATH  Google Scholar 

  19. Krawczuk, M., Ostachowicz, W.M.: A finite plate element for dynamic analysis of a cracked plate. Comput. Method. Appl. Mech. 115, 67–78 (1994)

    Article  Google Scholar 

  20. Su, R., Leung, A., Wong, S.C.: Vibration of cracked Kirchhoff’s plates. Key Eng. Mater. 145, 167–172 (1998)

    Google Scholar 

  21. Xu, Q., Chen, J., Li, J., Xu, G.: Study on the element with the hole and crack. Acta Mech. 225, 1915–1930 (2014)

    Article  Google Scholar 

  22. Laura, P., Grossi, R.O.: Transverse vibrations of rectangular plates with edges elastically restrained against translation and rotation. J. Sound Vib. 75, 101–107 (1981)

    Article  Google Scholar 

  23. Warburton, G.B., Edney, S.L.: Vibrations of rectangular plates with elastically restrained edges. J. Sound Vib. 95, 537–552 (1984)

    Article  Google Scholar 

  24. Gorman, D.J.: A general solution for the free vibration of rectangular plates resting on uniform elastic edge supports. J. Sound Vib. 139, 325–335 (1990)

    Article  Google Scholar 

  25. Li, W.L., Zhang, X., Du, J., Liu, Z.: An exact series solution for the transverse vibration of rectangular plates with general elastic boundary supports. J. Sound Vib. 321, 254–269 (2009)

    Article  Google Scholar 

  26. Xu, H.A., Du, J.T., Li, W.L.: Vibrations of rectangular plates reinforced by any number of beams of arbitrary lengths and placement angles. J. Sound Vib. 328, 3759–3779 (2010)

    Article  Google Scholar 

  27. Ye, T.G., **, G.Y., Su, Z., Chen, Y.H.: A modified Fourier solution for vibration analysis of moderately thick laminated plates with general boundary restraints and internal line supports. Int. J. Mech. Sci. 80, 29–46 (2014)

    Article  Google Scholar 

  28. Du, J., Li, W.L., Liu, Z., Yang, T., **, G.: Free vibration of two elastically coupled rectangular plates with uniform elastic boundary restraints. J. Sound Vib. 330, 788–804 (2011)

    Article  Google Scholar 

  29. Jiang, S., Li, W.L., Yang, T.: A spectro-geometric method for the vibration analysis of built-up structures. In: INTER-NOISE and NOISE-CON Congress and Conference Proceedings, vol. 246, pp. 948–953. Institute of Noise Control Engineering (2013)

  30. Xu, H., Li, W.L., Du, J.: Modal analysis of general plate structures. J. Vib. Acoust. 136, 21002 (2014)

    Article  Google Scholar 

  31. Dai, L., Yang, T., Li, W.L., **, G.: Dynamic analysis of circular cylindrical shells with general boundary conditions using modified Fourier series method. J. Vib. Acoust. 134, 41001–41012 (2012)

    Article  Google Scholar 

  32. Zhang, X.F., Li, W.L.: Vibration of arbitrarily-shaped triangular plates with elastically restrained edges. J. Sound Vib. 357, 195–206 (2015)

    Article  Google Scholar 

  33. Maruyama, K., Ichinomiya, O.: Experimental study of free vibration of clamped rectangular plates with straight narrow slits. JSME Int. J. 32, 187–193 (1989)

    Google Scholar 

  34. Ma, C., Huang, C.: Experimental and numerical analysis of vibrating cracked plates at resonant frequencies. Exp. Mech. 41, 8–18 (2001)

    Article  Google Scholar 

  35. Lee, U.: Spectral Element Method in Structural Dynamics. Wiley, Singapore (2009)

    Book  Google Scholar 

  36. Lee, Y.C.: Vibrations of rectangular thin plate with a crack via the Ritz method. M.S., National Chiao Tung University (2009)

  37. Pierre, C., Tang, D.M., Dowell, E.H.: Localized vibrations of disordered multi-span beams-theory and experiment. AIAA J. 25, 1249–1257 (1987)

    Article  Google Scholar 

  38. Shen, I.Y., Mote Jr., C.D.: On the mode splitting of degenerate mechanical systems containing cracks. J. Appl. Mech. Trans. ASME 60, 929–950 (1993)

    Article  MathSciNet  Google Scholar 

  39. Pierre, C., Dowell, E.H.: Localization of vibrations by structural irregularity. J. Sound Vib. 114, 549–564 (1987)

    Article  Google Scholar 

  40. Pierre, C.: Mode localization and eigenvalue loci veering phenomena in disordered structures. J. Sound Vib. 126, 485–502 (1988)

    Article  Google Scholar 

  41. Chen, P., Ginsberg, J.H.: On the relationship between veering of eigenvalue loci and parameter sensitivity of eigenfunctions. J. Vib. Acoust. 114, 141–148 (1992)

    Article  Google Scholar 

Download references

Acknowledgements

This research was supported by the Ministry of Science and Technology of China through Grant No. 2017YFC0306202, the Department of Science and Technology of Zhejiang Province through Grant No. 2018C04018, and the National High-end Foreign Expert Foundation of China through Grant No. GDT20173300032.

Author information

Authors and Affiliations

  1. Sound and Vibration Laboratory, College of Mechanical Engineering, Zhejiang University of Technology, 18 Chaowang Road, Hangzhou, 310014, China

    Tianming Huang, Huancai Lu, D. Michael McFarland & Jian Gong

  2. Department of Aerospace Engineering, University of Illinois at Urbana-Champaign, 104 South Wright Street, Urbana, IL, 61801, USA

    D. Michael McFarland & Lawrence A. Bergman

  3. Advanced Information Services, 98 Huiming Road, Fenghua District, Ningbo, 315500, China

    Wen L. Li

  4. Department of Mechanical Engineering, Wayne State University, 5050 Anthony Wayne Drive, Detroit, MI, 48202, USA

    Chin An Tan

Authors
  1. Tianming Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Huancai Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. D. Michael McFarland
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Wen L. Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Chin An Tan
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Lawrence A. Bergman
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Jian Gong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Huancai Lu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Additional Convergence Study Data

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huang, T., Lu, H., McFarland, D.M. et al. Natural frequency veering and mode localization caused by straight through–cracks in rectangular plates with elastic boundary conditions. Acta Mech 229, 4017–4031 (2018). https://doi.org/10.1007/s00707-018-2195-2

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-018-2195-2

Search

Navigation