Abstract
As outlined in the previous paper, an eigenstrain state due to an interstitial atom, acting as misfitting inclusion in the crystal lattice, may interact with a load stress state and/or a stress state due to a defect. Since the interstitial atoms can be assembled in a cylinder, as in the established case of a so-called Cottrell cloud, the according stress state can be investigated by a cylindrical inclusion with a general eigenstrain state. Both eigenstrain components belonging to the antiplane shear, however, were not dealt with in the past. According stress and deformation equations are now offered in analytical form in this addendum.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
To understand the diffusion process of interstitial atoms (later interstitials) near a defect, it is necessary
-
to know the stress field of the defect,
-
to know the stress field of the interstitials, which are placed at several distinct sites (e.g., the so-called octahedral or tetrahedral positions in a cubic lattice) and produce according eigenstrain fields. Here we refer to the recent paper [1].
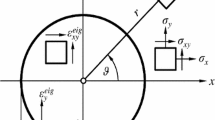
If we consider, e.g., an edge or screw dislocation, interstitials are densely assembled along the dislocation line, forming something like a cylindrical “cloud,” described by a cylinder with the dislocation line as z axis. As already outlined in the paper [2] (to which this paper is an “addendum”), the cylindrical “cloud” is represented as cylindrical inclusion with the radius R and an eigenstrain state with the components \(\varepsilon _{xx}^\mathrm{{eig}} ,\varepsilon _{yy}^\mathrm{{eig}} ,\varepsilon _{zz}^\mathrm{{eig}} ,\varepsilon _{xy}^\mathrm{{eig}} \). (The coordinates of the cross section are x, y and z is the coordinate in the axial direction.) The paper [2] provides the reader with the stress state inside and outside of the inclusion in analytical form. However, it has become recently evident that also eigenstrain terms \(\varepsilon _{xz}^\mathrm{{eig}} \) and \(\varepsilon _{yz}^\mathrm{{eig}} \) may occur, which are not treated in [2]. The goal of this addendum is to provide the reader also with the according stress state inside and outside of the cylindrical inclusion.
2 Solution concept
The notation is the same as in [2]. According to Eshelby’s seminal work on inclusions, see the references in [2]; the eigenstress state is spatially constant in the cylindrical inclusion. The inside eigenstress state can immediately be calculated in Cartesian coordinates (\(x,y,r=\sqrt{x^{2}+y^{2}}\), z axis of rotation), according to [3, 4], aspect ratio \(\alpha \rightarrow \infty \), Eqs. (4.1–2) and \((\hbox {A}4)_{4}\) there, with the shear modulus \(G=E/2\left( {1+\nu } \right) \), E Young’s modulus, \(\nu \) Poisson’s ratio, as
As boundary condition at the interface (i.e., the radial position \(r=R)\), we use the traction vector \(\mathbf{t}\), which follows with the inside stress tensor \(\varvec{\upsigma }\) (with the only nonzero elements from Eq. (1)) and the normal vector n with the components \(\left( {x/R,y/R,0} \right) \) as \(\varvec{\upsigma }{\cdot } \mathbf{n}{=}{} \mathbf{t}\). The only nonzero component of t is
To solve the problem for the stress state outside the inclusion, where no eigenstrain is active, cylindrical coordinates, r and \(\vartheta \), are used. The only displacement is that in z direction, \(w\left( {r,\vartheta } \right) \), which is independent of the z coordinate. As stress components only \(\sigma _{rz} \) and \(\sigma _{\vartheta z} \) exist. Theory of elasticity, see, e.g., [5], Sect. 4.9.1, teaches the equilibrium equation as
and [5], Sect. 5.5.3, Hooke’s law as
Combining Eqs. (3) and (4) one finds with \(w=Cf\left( r \right) g\left( \vartheta \right) \), C is an integration constant, \(f\left( r \right) \) has to be derived, \(g\left( \vartheta \right) =\cos \vartheta \) or \(g\left( \vartheta \right) =\sin \vartheta \), \({g}''\left( \vartheta \right) =-g\left( \vartheta \right) \), the following differential equation
with the solution
Remark: We denote now first derivatives by \(^\prime \) and second derivatives by\(''\).
Note that two eigenstrain cases are superposed, see Eq. (1). Therefore, two superposed displacements exist as \(w_x \) (subscript x according to \(\varepsilon _{xz}^\mathrm{{eig}} )\) with \(C=C_x \), \(g\left( \vartheta \right) =g_x \left( \vartheta \right) \) and \(w_y \) (subscript y according to \(\varepsilon _{yz}^\mathrm{{eig}} )\) with \(C_y ,g_y \left( \vartheta \right) \). The total outside component \(\sigma _{rz} \), Eq. (4)\(_{1}\), reads with Eq. (6) for both cases as
Since a jump of the traction vector t must not exist at the interface \(r=R\), \(t_z =\sigma _{rz} \), comparison between Eqs. (2) with \(\cos \vartheta =x/r\), \(\sin \vartheta =y/r\) and (7) yields
The stress state follows with Eq. (4) as
It may be of interest to mention that a decay of the stress state proportional to \({R^{2}}/{r^{2}}\) in outside can also be seen in [6], Sect. 4.1.
A final note: If a plane strain configuration (it is, e.g., a disk of infinite extension in the x, y plane with no constraints in the x, y direction and a finite thickness h) is assumed, with the z axis being the axis of the cylindrical inclusion, \(0\le z\le h\), then the displacement field \(w=w_x +w_y \),
must be suppressed at \(z=h\). However, the average value \(\tilde{w}\) of \(w\left( {r,\vartheta } \right) \) is zero, due to the integration with respect to \(\vartheta \). Therefore, according to St. Venant’s principle, only a local stress state, i.e., \(\sigma _{zz} \) and corresponding values of \(\sigma _{xx} ,\sigma _{yy} \), will develop due to \(w\equiv 0\) at \(z=h\), which, however, will disappear in certain distance from the surface at \(z=h\). Therefore, we omit, for the sake of simplicity, any estimation of the stress component \(\sigma _{zz}\).
References
Svoboda, J., Zickler, G.A., Fischer, F.D.: An innovative concept for interstitial diffusion in stressed crystals. Int. J. Solids Struct. 134, 173–180 (2018). https://doi.org/10.1016/j.ijsolstr.2017.10.036
Fischer, F.D., Zickler, G.A., Svoboda, J.: Elastic stress–strain analysis of an infinite cylindrical inclusion with eigenstrain. Arch. Appl. Mech. 88, 453–460 (2018). https://doi.org/10.1007/s00419-017-1318-x
Böhm, H.J., Fischer, F.D., Reisner, G.: Evaluation of elastic strain energy of spheroidal inclusions with uniform volumetric and shear eigenstrains. Erratum. Scripta Mater. 36, 1053–1059 (1997)
Böhm, H.J., Fischer, F.D., Reisner, G.: Evaluation of elastic strain energy of spheroidal inclusions with uniform volumetric and shear eigenstrains. Scripta Mater. 49, 107 (2003)
Mal, A.K., Singh, S.J.: Deformation of Elastic Solids. Prentice-Hall, Englewood Cliffs (1991)
**, X., Keer, L.M., Wang, Q.: A closed-form solution for the Eshelby tensor and the elastic field outside an elliptic cylindrical inclusion. ASME J. Appl. Mech. 78, 031009-1-6 (2011)
Acknowledgements
Open access funding provided by Montanuniversity Leoben.
Author information
Authors and Affiliations
Corresponding author
Additional information
This is an addendum article to https://springer.longhoe.net/article/10.1007/s00419-017-1318-x.
Appendix: Eigenstress fields in a Cartesian coordinate system
Appendix: Eigenstress fields in a Cartesian coordinate system
The eigenstress field is expressed in Cartesian coordinates using the abbreviations \(\bar{{x}}=x/R,\bar{{y}}=y/R\) and \(\bar{{r}}=r/R\)
Inside
Outside
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Fischer, F.D., Zickler, G.A. & Svoboda, J. Stress–strain analysis of the antiplane shear problem for an infinite cylindrical inclusion with eigenstrain: an addendum to Arch. Appl. Mech. 2018 . Arch Appl Mech 88, 1209–1211 (2018). https://doi.org/10.1007/s00419-018-1367-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00419-018-1367-9