Abstract
We use geometric methods of equivariant dynamical systems to address a long-standing open problem in the theory of nematic liquid crystals, namely a proof of the existence and asymptotic stability of kayaking periodic orbits in response to steady shear flow. These are orbits for which the principal axis of orientation of the molecular field (the director) rotates out of the plane of shear and around the vorticity axis. With a small parameter attached to the symmetric part of the velocity gradient, the problem can be viewed as a symmetry-breaking bifurcation from an orbit of the rotation group \(\mathrm{SO}(3)\) that contains both logrolling (equilibrium) and tumbling (periodic rotation of the director within the plane of shear) regimes as well as a continuum of neutrally stable kayaking orbits. The results turn out to require expansion to second order in the perturbation parameter.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Nematic liquid crystals, regarded as fluids in which the high aspect ratio, rigid, rod molecules require descriptive variables for orientation as well as position, are observed to exhibit a wide range of prolonged unsteady dynamical responses to steady shear flow. The mathematical study of these phenomena in principle involves the Navier–Stokes equations for fluid flow coupled with equations representing molecular alignment and nonlocal interactions between rod molecules, typically leading to PDE systems currently intractable to rigorous analysis on a global scale and resolved only through local analysis and/or numerical simulation. It becomes appropriate therefore to deal with simpler models as templates for capturing some of the dynamical regimes of interest and their responses to physical parameters. Stability and bifurcation behaviours that are robust for finite-dimensional dynamical systems, and that numerically reflect the same orbits of interest (specifically, kayaking orbits) in infinite-dimensional systems, provide a framework for extension of rigorous results to the infinite-dimensional systems.
Much of the work on dynamics of liquid crystals (and more generally, rigid large aspect ratio polymers) in fluid flow rests on models proposed by Hess [41] and Doi [19] that consider the evolution of the probability density on the 2-sphere (more accurately, projective space \({{\mathbb {R}}}{\mathrm P}^2\)) representing unoriented directions of molecular alignment with the molecules regarded as rigid rods. Extensive theoretical and numerical investigations ([6, 21, 22, 47, 54, 55, 62, 64,65,66] to cite only a few) of these and related nematic director or orientation tensor models in 2D or 3D reveal a wide range of periodic molecular dynamical regimes with evocative names [47] logrolling, tumbling, wagging and kayaking according to the behaviour (steady versus periodic) of the principal axis of molecular orientation (the nematic director) relative to the shear (flow velocity and velocity gradient) plane and vorticity axis (normal to the shear plane). Tumbling orbits, for which the principal axis of molecular orientation rotates periodically in the shear plane, are seen to be stable at low shear rates, but become unstable to out-of-plane perturbations and give way to kayaking orbits, for which the principal molecular axis is transverse to the shear plane, and rotates around the vorticity axis, reminiscent of the motion of the paddles propelling a kayak along the shear flow of a calm stream. The limiting case is logrolling, a stationary state where the principal axis of the rod ensemble collapses onto the vorticity axis, while wagging corresponds to oscillations (but not complete rotations) of the molecular orientation in the shear plane about some mean angle, although wagging regimes do not appear in our analysis. We note very recent experimental results [31] coupled with the high-resolution numerical results of the Doi-Hess kinetic theory [30] that provide overwhelming evidence that the kayaking orbit is responsible for the anomalous shear-thickening response of a high aspect ratio, rodlike, liquid crystal polymer with the acronym PBDT. The papers [27, 31] give extensive lists of literature references.
In the particular case of a steady shear flow and spatially homogeneous liquid crystal in a region in \({{\mathbb {R}}}^3\), the PDEs describing the evolution of orientational order can be simplified to an autonomous ODE in the setting of the widely-used \({ Q}\)-tensor model [17, 59, 72] for nematic liquid crystals. The assumption of spatial homogeneity of course rules out many important applications, to display technology for example, but nevertheless gives a worthwhile approximation in local domains of homogeneity (monodomains) away from boundaries and defects. In this setting the propensity of a molecule to align in any given direction in \({{\mathbb {R}}}^3\) is represented by an order tensor \({ Q}\) belonging to the 5-dimensional space V of traceless symmetric \(3\times 3\) matrices,
where \(\{\,\}^{\mathtt {t}}\) and \(\,\mathrm{tr}\,\) denote transpose and trace respectively. The tensor \({ Q}\) is interpreted as the normalised second moment of a more general probability distribution on \({{\mathbb {R}}}{\mathrm P}^2\). All such \({ Q}\)-tensor models can be associated with a moment-closure approximation of the Smoluchowski equation for the full orientational distribution function [27]. The derivation of the equation yields technical problems concerning the approximation of higher-order moments, a topic of some discussion in the literature: see [23, 27, 46, 48] for example. In this context the dimensionless equation for the evolution of the orientational order takes the general form
as an equation in \(V\cong {{\mathbb {R}}}^5\); here \([W,{ Q}\,]=W\!{ Q}-{ Q}W\).Footnote 1 On the right hand side of (1.2) the first term represents the molecular interactions in the absence of flow, derived for example from a Maier–Saupe interaction potential or Landau–de Gennes free energy: thus G is a frame-indifferent vector field in V. In the second term, W denotes the vorticity tensor, the anti-symmetric part of the (spatially homogeneous) velocity gradient, providing the rotational effect of the flow with constant coefficient \(\omega \). In the third term \(\varvec{L}(Q)\) is a linear transformation \(V\rightarrow V\) applied to the rate-of-strain tensor D, the symmetric part of the velocity gradient, and represents the molecular aligning effect of the flow: the linearity in D is a simplifying assumption. Here \(\varvec{L}(Q)\) depends (not necessarily linearly) on \({ Q}\), and \(\varvec{L}({ Q})D\) is frame-indifferent with respect to simultaneous coordinate choice for the flow and the molecular orientation. The coefficients \(\omega \) and \(\beta \) are constant scalars that depend on the physical characteristics of the liquid crystal molecule as well as the flow. In this study we take \(\omega \) as fixed, and regard \(\beta \) as a variable parameter.
In the Olmsted–Goldbart model [61] used in [12, 75] the term \(\varvec{L}({ Q})D\) is simply a constant scalar multiple of D. A more detailed model for \(\varvec{L}({ Q})D\) is the basis of a series of studies by the second author and co-workers [26,27,28,29,30, 48] as well as by many other authors [8, 35, 56, 63]. We draw attention also to the earlier theoretical work [52, 53] assuming a general form for \(\varvec{L}({ Q})D\) and where similar methods to ours are used to study equilibrium states (uniaxial or biaxial), although the question of periodic orbits in general and kayaking orbits in particular is hardly addressed, the existence of the latter having yet to be discovered.
We remark that although in this paper our underlying assumption is of spatial homogeneity, there have been studies of nematic liquid crystals dynamics in a nonhomogeneous environment; see, among others, [13] for analytical results and [77] for numerical simulations.
A particular model of the form (1.2) that ‘combines analytic tractability with physical relevance’ [60] is the Beris–Edwards model [4], a basis for some more recent investigations [18, 20, 60, 76] in both the PDE and ODE settings. Here G is the negative gradient of a degree four Landau-de Gennes free energy function, while the term \(\varvec{L}({ Q})D\) takes the form
in which we use the notation
for any matrices \(H,K\in V\); here and elsewhere I denotes the \(3\times 3\) identity matrix. Observe that (1.3) is a linear combination of a constant, a linear and a quadratic term in \({ Q}\), that we denote (without their coefficients) respectively by \(\varvec{L}^c({ Q})D,\,\varvec{L}^l(Q)D,\,\varvec{L}^q({ Q})D\). In this paper we initially work with an arbitrary choice of smoothFootnote 2 field \(\varvec{L}({ Q})D\) subject to a natural assumption of frame-indifference. We then replace this by an arbitrary linear combination
which helps to keep track of the analysis, and also enables the results to apply to simpler models for which one or more of the \(m_i\) may be zero. For the Beris–Edwards model (1.3) the ratios are \(( m_c: m_l: m_q)=(2/3:1:-2)\), while for the Olmsted–Goldbart model [61] the ratios are (1 : 0 : 0) and for the model in [54] they are \((\sqrt{3/10}:3/7:0)\). Moreover, in “Appendix B” we pursue the analysis for general \(\varvec{L}({ Q})D\), using the 7-term expression assumed for example in [52, 53], and show that with the exception of one term the results are the same as those for (1.5) albeit with different interpretation of the coefficients \( m_c, m_l, m_q\). The exceptional term (being the symmetric traceless form of \(Q^2D\)) also fits into our overall framework as shown in the expressions (B.18) and (B.19) with (B.2).
When \(\beta =0\) the equation (1.2) represents the co-rotational case or long time regime, as discussed in [60]. If \({ Q}^*\in V\) satisfies \(G({ Q}^*)=0\) then frame-indifference of G, interpreted as equivariance (covariance) of G under the action of the rotation group \(\mathrm{SO}(3)\) on V, implies that every element \({ Q}\) of the \(\mathrm{SO}(3)\) group orbit \({\mathscr {O}}\) of \(Q^*\) also satisfies \(G({ Q})=0\). If moreover \([W,{ Q}^*]=0\) then \(F({ Q}^*,0)=0\) and so \({ Q}^*\) is an equilibrium for (1.2): the rotational component of the shear flow leaves \({ Q}^*\) fixed. This implies that \({ Q}^*\) has two equal eigenvalues, and if these are less than the third (principal) eigenvalue then \({ Q}^*\) represents a logrolling regime. Moreover, \([W,{ Q}\,]\) is tangent to \({\mathscr {O}}\) for every \(Q\ne { Q}^*\in {\mathscr {O}}\) and so \({\mathscr {O}}\) (which is topologically a copy of \({{\mathbb {R}}}{\mathrm P}^2\)) is an invariant manifold for the flow on V generated by (1.2) when \(\beta =0\). The dynamical orbit of every such \(Q\in {\mathscr {O}}\) is periodic, as it coincides with the group orbit of rotations about the axis orthogonal to the shear plane; in the language of equivariant dynamics [15, 25, 43] it is a relative equilibrium. All of these periodic orbits represent kayaking regimes, except for a unique orbit representing tumbling, and they are neutrally stable with respect to the dynamics on \({\mathscr {O}}\), as also is the logrolling equilibrium \({ Q}^*\). We discuss this geometry of the \(\mathrm{SO}(3)\)-action on V in more detail below; it plays a central role in what follows, as it must do in any global study of the system (1.2), an observation of course recognised by other authors [26, 52, 53].
There are a few rigorous mathematical proofs of the existence of tumbling limit cycle orbits with limiting assumptions. By positing 2D rods, both with a tensor model [48] and with the stochastic ODE [40], proofs follow from the Poincaré-Bendixson theorem; for 3D rods with a tensor model the proof in [12] uses geometric arguments on in-plane tensors. Until now, there has been no proof of existence of (stable) kayaking orbits, and the purpose of this paper is to provide a proof for second-moment tensor models (1.2), (1.5) at low rates of molecular interaction (although not necessarily low shear rates). We thus consider a dynamical regime different from those considered by other authors in numerical simulations such as [27, 66]. A regime analogous to ours in considered in the theoretical work [52, 53] using very similar methods, but in that case the molecules are assumed biaxial and it is equilibria rather than periodic orbits that are sought.
The approach we take is to regard \(\beta \) as a small parameter and view (1.2) as a perturbation of the co-rotational case. This enables us to use tools from equivariant bifurcation theory [15, 33, 43, 69, 70] and in particular Lyapunov–Schmidt reduction over the group orbit \({\mathscr {O}}\) to obtain criteria for the persistence or otherwise of the periodic orbits of the co-rotational case after perturbation, and to determine the stability or otherwise of the resulting logrolling, tumbling and kayaking dynamics. Our general results are independent of the choice of the interaction field G, given that it is frame-indifferent and the logrolling state is an equilibrium: \(G({ Q}^*)=0\) (Assumptions 1, 2 in Section 2) and also that the eigenvalues \(\lambda ,\mu \) of the linearisation of G at \({ Q}^*\) normal to \({\mathscr {O}}\) are real and nonzero (Assumption 3 in Section 3). In addition we require a natural condition of frame-indifference for the perturbing field \(\varvec{L}({ Q})D\) (Assumption 4 in Section 3). Finally, the stability results require \(\lambda ,\mu <0\) (Assumption 5 in Section 7). However, our methods do not allow us to make deductions when \(\beta \) is large compared with the rotational coefficient \(\omega \). Other limit cycles are possible, and indeed are routinely observed numerically.
Our main result is Theorem 7.7 with Remark 7.9, showing that the existence of a limit cycle kayaking orbit after perturbation depends on the ratio \(\lambda /\mu \) as well as the size of the product \(\lambda \mu \) relative to the rotation coefficient \(\omega \). We show also in Corollary 7.8 that for the Beris–Edwards and Olmsted–Goldbart models the kayaking orbit is linearly stable without further assumption.
This paper is organised as follows. In Section 2 we discuss symmetries of the model and key features of the action of \(\mathrm{SO}(3)\) on V that it inherits from the usual action on \({{\mathbb {R}}}^3\). Of particular importance are the tangent and normal subspaces to the group orbit \({\mathscr {O}}\). Section 3 gives initial results showing the persistence of log-rolling and tumbling regimes after perturbation, and introduces the rotating coordinate system convenient for further analysis. In Section 4 a natural Poincaré section for the (dynamical) flow near \({\mathscr {O}}\) is described and relevant first-order derivatives of the associated Poincaré map are calculated and shown to vanish. Lyapunov–Schmidt reduction is applied in Section 5 to obtain a real-valued bifurcation function defined on a meridian of \({\mathscr {O}}\). This function happens to vanish to first order in \(\beta \) and so we are obliged to pursue the \(\beta \)-expansion to second order. In Section 6 we choose \(\varvec{L}({ Q})D\) explicitly as (1.5) and evaluate these second order terms. Finally, in Section 7 the zeros of the bifurcation function are found and the conditions for existence and stability of kayaking motion are determined. For the specific cases of the Beris–Edwards and Olmsted–Goldbart models with Landau–de Gennes free energy the criteria for existence and stability of kayaking orbits are stated explicitly. Following a brief concluding section there are Appendices giving some technical results arising from symmetries that simplify the main calculations, as well as a discussion of how a fully general form of the molecular alignment term \(\varvec{L}({ Q})D\) fits into the framework of our analysis.
2 Geometry and Symmetries of the System
The molecular interaction field G is independent of the coordinate frame and therefore equivariant (covariant) with respect to the action of the rotation group \(\mathrm{SO}(3)\) on V by conjugation induced from the natural action on \({{\mathbb {R}}}^3\). Therefore our first working assumption in this paper is the following:
Assumption 1
\( {\widetilde{R}}G({ Q}) = G({\widetilde{R}}{ Q}) \) for all \({ Q}\in V\) and \(R\in \mathrm{SO}(3)\)
where we use the notation
Further discussion of equivariant maps, in particular relating to the action of \(\mathrm{SO}(3)\) on V that we shall use extensively in this paper, is given in “Appendix A”.
Choosing coordinates \((x,y,z)\in {{\mathbb {R}}}^3\) so that the shear flow velocity field has the form k(y, 0, 0) for constant \(k\ne 0\) the velocity gradient tensor is
with symmetric and anti-symmetric parts kD/2 and \(-kW/2\) respectively, where
Without loss of generality we take \(k=2\) since the coefficients \(\omega \) and \(\beta \) in (1.2) are at present arbitrary. The rotational component W corresponds to infinitesimal rotation about the z-axis.
A nonzero matrix \({ Q}\in V\) is called uniaxial if it has two equal eigenvalues less than the third, in which case it is invariant under rotations about the axis determined by the third eigenvalue. Matrices with three distinct eigenvalues are biaxial. In this paper an important role is played by the uniaxial matrix
where \(0<a<1/3\) for which the principal axis (largest eigenvalue) is the z-axis and about which \({ Q}^*\) is rotationally invariant. We take \(a>0\) to ensure that \({ Q}^*\) is uniaxial, and the upper bound on a is imposed for physical reasons since the second moment of the probability distribution defining the \({ Q}\)-tensor has eigenvalues in the interval [0, 1] and so those of \({ Q}\) are no greater than 2/3: see [3] for example. We exclude \(a=1/3\) as we shall need to work in a neighbourhood of \({ Q}^*\).
Our second underlying assumption is that this phase is an equilibrium for the system (1.2) in the absence of flow, that is when \(\omega =\beta =0\). In other words, we have
Assumption 2
The coefficient a is such that \(G({ Q}^*)=0\).
With this assumption, the equivariance property of G implies that G vanishes on the entire \(\mathrm{SO}(3)\)-orbit \({\mathscr {O}}\) of \({ Q}^*\) in V, and \({\mathscr {O}}\) is an invariant manifold for the flow on V generated by (1.2) with \(\beta =0\). The dynamical orbits on \({\mathscr {O}}\) coincide with the group orbits of rotation about the z-axis under which \({ Q}^*\) remains fixed, this being the only fixed point on \({\mathscr {O}}\) since if \({ Q}\in {\mathscr {O}}\) and \([W,Q\,]=0\) then \({ Q}\) is a scalar multiple of and hence equal to \({ Q}^*\).
2.1 Rotation Coordinates: the Veronese Map
For calculation purposes it is natural and convenient to take coordinates in V geometrically adapted to \({\mathscr {O}}\). We do this in a standard way by representing the orbit \({\mathscr {O}}\) of \({ Q}^*\) as the image of the unit sphere \({{\mathbb {S}}}^2\subset {{\mathbb {R}}}^3\) under the map
where again \({}^{\mathtt {t}}\) denotes matrix (or vector) transpose. Here \({\mathscr {V}}\) is the projection to V of the case \(n=3\) of the more general Veronese map construction \({{\mathbb {R}}}^n\rightarrow {{\mathbb {R}}}^m\) with \(m=\left( {\begin{array}{c}n\\ 2\end{array}}\right) \) and it represents \({\mathscr {O}}\) as a Veronese surface in \({{\mathbb {R}}}^5\): see for example [34] or [39]. It is straightforward to check that \({\mathscr {V}}\) is equivariant with respect to the actions of \(\mathrm{SO}(3)\) on \({{\mathbb {R}}}^3\) and V, that is, if \(R\in \mathrm{SO}(3)\) then
for all \({{\mathbf {z}}}\in {{\mathbb {R}}}^3\). Note that \({ Q}^*={\mathscr {V}}({{\mathbf {e}}}_3)\) where \(\{{{\mathbf {e}}}_1,{{\mathbf {e}}}_2,{{\mathbf {e}}}_3\}\) is the standard basis in \({{\mathbb {R}}}^3\), and that \({\mathscr {V}}({{\mathbf {e}}}_1)\) and \({\mathscr {V}}({{\mathbf {e}}}_2)\) are obtained from \({ Q}^*\) by permutation of the diagonal terms.
On V we have a standard inner product given by \(\left\langle H,K\right\rangle =\mathrm{tr}(H^{\mathtt {t}}K)=\mathrm{tr}(HK)\). However, the Veronese map is quadratic and does not preserve inner products. Nevertheless, up to a constant factor, its derivative does preserve inner products on tangent vectors to \({{\mathbb {S}}}^2\). Explicitly,
with the dot denoting usual inner product in \({{\mathbb {R}}}^3\), from which it follows that for \({{\mathbf {z}}}\in {{\mathbb {S}}}^2\) and \({{\mathbf {u}}},{{\mathbf {v}}}\in {{\mathbb {R}}}^3\) orthogonal to \({{\mathbf {z}}}\),
Observe that the restriction of \({\mathscr {V}}\) to \({{\mathbb {S}}}^2\) is a double cover \({{\mathbb {S}}}^2\rightarrow {\mathscr {O}}\) since \({\mathscr {V}}(-{{\mathbf {z}}})={\mathscr {V}}({{\mathbf {z}}})\) for all \({{\mathbf {z}}}\in {{\mathbb {R}}}^3\). Through \({\mathscr {V}}\) the familiar latitude and longitude coordinates on \({{\mathbb {S}}}^2\) go over to a corresponding coordinate system on \({\mathscr {O}}\). Any \({{\mathbf {z}}}\ne {{\mathbf {e}}}_3\in {{\mathbb {S}}}^2\) can be written using spherical coordinates as
for unique \(\theta \bmod \pi \) and \(\phi \bmod 2\pi \), where \(R_j(\psi )\) denotes rotation by angle \(\psi \) around the jth axis in \({{\mathbb {R}}}^3\), \(j=1,2,3\), so that, in particular,
Hence by (2.6) and equivariance (2.3) any \(Z\in {\mathscr {O}}\) can be written (not uniquely) as
for some \({{\mathbf {z}}}\in {{\mathbb {S}}}^2\), as the counterpart of (2.6) using rotations \({\widetilde{R}}\) on V in place of R on \({{\mathbb {R}}}^3\). We shall make frequent use of this notation throughout the paper.
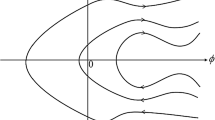
By analogy with \({{\mathbb {S}}}^2\) we call each closed curve \(\theta =\mathrm{const}\ne 0 \bmod \pi \) on \({\mathscr {O}}\) a latitude curve and each curve \(\phi =\mathrm{const}\) on \({\mathscr {O}}\) a meridian. It follows from (2.5) that all latitude curves are orthogonal to all meridians. The case \(\theta =0\bmod \pi \) corresponds to \(Q^*\), and so we think of \(Q^*\) as the north pole of \({\mathscr {O}}\cong {{\mathbb {R}}}{\mathrm P}^2\).
Remark 2.1
The expression (2.6) provides the standard spherical coordinates on \({{\mathbb {S}}}^2\). Standard Euler angle coordinates on SO(3) are obtained as the composition of three rotation matrices; the Veronese coordinates for \({\mathscr {O}}\) provided by (2.7) are obtained by disregarding one of those rotations.
2.2 Isotypic Decomposition
The rotation symmetry of \({\mathscr {O}}\) about the north pole \({ Q}^*\) plays a fundamental role in our analysis of (1.2) for sufficiently small nonzero \(\beta \), and enables us to choose coordinates in V that are strongly adapted to the inherent geometry of the problem. More generally, for any \({{\mathbf {z}}}\in {{\mathbb {S}}}^2\) let
denote the isotropy subgroup of \({{\mathbf {z}}}\) (namely the group of rotations about the \({{\mathbf {z}}}\)-axis) under the natural action of \(\mathrm{SO}(3)\) on \({{\mathbb {R}}}^3\). Equivariance of \({\mathscr {V}}\) implies that \(\Sigma _{{\mathbf {z}}}\) also fixes \(Z={\mathscr {V}}({{\mathbf {z}}})\) in \({\mathscr {O}}\) under the conjugacy action, and moreover Z is an isolated fixed point of \(\Sigma _{{\mathbf {z}}}\) on \({\mathscr {O}}\) since \({{\mathbf {z}}}\) is an isolated fixed point of \(\Sigma _{{\mathbf {z}}}\) on \({{\mathbb {S}}}^2\).
At this point it is convenient to develop some further machinery from the theory of linear group actions to describe key features of the geometry highly relevant to our analysis. Introductions to the theory of group actions and orbit structures can be found, for example, in [1, 14, 58]. We shall make much use of the further fact that corresponding to the action of \(\Sigma _{{\mathbf {z}}}\) on V there is an isotypic decomposition of V (for theoretical background to this notion see for example [15, 25, 33]) into the direct sum of three \(\Sigma _{{\mathbf {z}}}\)-invariant subspaces
on each of which \(\Sigma _{{\mathbf {z}}}\) acts differently: the element \(R_{{\mathbf {z}}}(\psi )\in \Sigma _{{\mathbf {z}}}\) denoting rotation about the \({{\mathbf {z}}}\)-direction through angle \(\psi \) acts on \(V_k^Z\) by rotation through \(k\psi \) for \(k=0,1,2\). In particular, with \({{\mathbf {z}}}={{\mathbf {e}}}_3\) and \(Z=Q^*\) writing \(V_k^*=V_k^{Q^*}\) we have
where the mutually orthogonal matrices \(E_0, E_1(\alpha ),E_2(\alpha )\) are given by
and we set
Here \(R_3(\phi )\) acts on \(V_1^*\) and \(V_2^*\) by
where we keep in mind that \(E_2(\alpha )\) is defined in terms of \(2\alpha \). For \(Z = Z(\theta ,\phi )\) as in (2.7) we use the notation
and
so that
A consequence of \(\mathrm{SO}(3)\)-equivariance is that for \(Z\in {\mathscr {O}}\) the derivative \({\mathrm D}G(Z):V\rightarrow V\) respects the decomposition (2.8) and commutes with the \(\Sigma _{{\mathbf {z}}}\)-rotations on each component. A further important consequence that simplifies several later calculations is the following:
Proposition 2.2
If a differentiable function \(f:V\rightarrow {{\mathbb {R}}}\) is invariant under the action of \(\Sigma _{{\mathbf {z}}}\) then its derivative \({\mathrm D}f(Z):V\rightarrow {{\mathbb {R}}}\) annihilates \(V_1^Z\oplus V_2^Z\).
Proof
If \(f({\widetilde{R}}{ Q})=f({ Q})\) for all \(R\in \Sigma _{{\mathbf {z}}}\) and \({ Q}\in V\) then \({\mathrm D}f({\widetilde{R}}{ Q}){\widetilde{R}}={\mathrm D}f({ Q})\) and so in particular \({\mathrm D}f(Z){\widetilde{R}}={\mathrm D}f(Z)\) for all \(R\in \Sigma _{{\mathbf {z}}}\). The only linear map \(V\rightarrow {{\mathbb {R}}}\) invariant under all rotations of \(V_1^Z\) and of \(V_2^Z\) must be zero on those components. \(\quad \square \)
2.3 Alignment Relative to the Flow
Since the element \(R_3(\pi )\in \mathrm{SO}(3)\) acts on \(V_k^*\) by a rotation through \(k\pi \) it follows that \(V_0^* \oplus V_2^*\) is precisely the fixed-point space for the action of \(R_3(\pi )\) on V. Thus \({ Q}=(q_{ij})\in V\) is fixed by \({\widetilde{R}}_3(\pi )\) if and only if \(q_{13}=q_{23}=0\), in which case \(q_{33}\) is an eigenvalue with eigenspace the z-axis and the other eigenspaces lie in (or coincide with) the x, y-plane. It is immediate to check that if \({ Q}=pE_0 + qE_2(\alpha )\) then the eigenvalues of \({ Q}\) are \(2p/\sqrt{6}\) and \((-p\pm \sqrt{3}q)/\sqrt{6}\) and so \({ Q}\) has two equal eigenvalues precisely when
In the first case \({ Q}=pE_0\), while in the second case the eigenvalues are \(2p/\sqrt{6}\) (repeated) and \(-4p/\sqrt{6}\) so that if \(p<0\) then \({ Q}\) is uniaxial with principal axis lying in the x, y-plane.
From the point of view of the liquid crystal orientation relative to the shear flow such matrices \({ Q}\) are called in-plane; nonzero matrices which are not in-plane are called out-of-plane. This agrees with standard terminology where tumbling and wagging dynamical regimes are described as in-plane (see [21, 64] for example), while logrolling and kayaking are out-of-plane.
Let C denote the equator \(\{\theta =\pi /2\}\) of \({{\mathbb {S}}}^2\), and let \({{\mathscr {C}}}={\mathscr {V}}(C)\subset {\mathscr {O}}\) which we also call the equator of \({\mathscr {O}}\). It is straightforward to check that
Proposition 2.3
Proof
Since \(V_0^*\oplus V_2^*\) is the orthogonal complement to \(V_1^*\) we see \({ Q}\in V_0^*\oplus V_2^*\) if and only if \(\left\langle { Q},E_1(\alpha )\right\rangle =0\) for all \(\alpha \). If \(Z={\mathscr {V}}({{\mathbf {z}}})\in {\mathscr {O}}\), then
With \({{\mathbf {z}}}=(\cos \phi \sin \theta ,\sin \phi \sin \theta ,\cos \theta )^{\mathtt t}\) in usual spherical coordinates we find \({{\mathbf {z}}}\cdot E_1(\alpha ){{\mathbf {z}}}=(1/\sqrt{2}) \sin 2\theta \cos (\phi -\alpha )\) which vanishes for all \(\alpha \) just when \(\sin 2\theta =0\), that is \(\theta =0\) or \(\theta =\pi /2\) corresponding to \(Z={ Q}^*\) or \(Z\in {{\mathscr {C}}}\), respectively. \(\square \)
When \(\beta =0\) the equation (1.2) reduces on \({\mathscr {O}}\) to
since \(G({ Q})=0\) for \({ Q}\in {\mathscr {O}}\), giving solution curves \(t\mapsto {\widetilde{R}}_3(\omega t){ Q}\) each of which has least period \(2\pi /\omega \) apart from the equilibrium \(Q^*\) and the equator \({{\mathscr {C}}}\): this has least period \(\pi /\omega \), the equator C of \({{\mathbb {S}}}^1\) being a double cover of \({{\mathscr {C}}}\) via the Veronese map. A matrix \({ Q}\in {{\mathscr {C}}}\) is in-plane and its dynamical orbit corresponds to steady rotation of period \(\pi /\omega \) about the origin in the shear plane, and so \({{\mathscr {C}}}\) represents a tumbling orbit. All latitude curves of \({\mathscr {O}}\) other than the equator \({{\mathscr {C}}}\) represent kayaking orbits of period \(T_0=2\pi /\omega \) and of neutral stability on \({\mathscr {O}}\) and so most of them are unlikely to persist for \(\beta \ne 0\). The geometry can be visualised as follows: removing the poles at \({{\mathbf {z}}}=\pm \,{{\mathbf {e}}}_3\) from \({{\mathbb {S}}}^2\) leaves an (open) annulus foliated by circles of latitude, so that removing \({ Q}^*\) from \({\mathscr {O}}\) leaves a Möbius strip foliated by closed latitude curves each of which traverses the strip twice since \(Z(\pi /2+\theta ,\phi )=Z(\pi /2-\theta ,\phi +\pi )\), except for the ‘central curve’ \({{\mathscr {C}}}\) given by \(\theta =0\) which traverses it only once.
2.4 Tangent and Normal Vectors to the Group Orbit \({\mathscr {O}}\)
The 2-dimensional tangent space \({\mathscr {T}}^Z\) to \({\mathscr {O}}\) at \(Z\in {\mathscr {O}}\) is spanned by infinitesimal rotations of Z, that is,
where
with
However, for \(Z\ne { Q}^*\) the tangent space \({\mathscr {T}}^Z\) is also spanned by the tangents at Z to the meridian and latitude curve of \({\mathscr {O}}\) through Z.
Lemma 2.4
Let \(Z\in {\mathscr {O}}\) with \(Z\ne { Q}^*\). The (1-dimensional) tangent spaces at Z to the meridian and latitude curve of \({\mathscr {O}}\) through Z are spanned by \(E_{11}^Z\) and \(E_{12}^Z\), respectively.
Proof
If \(\phi =0\) the vectors \(R_2(\theta )\,{{\mathbf {e}}}_1\) and \({{\mathbf {e}}}_2=R_2(\theta )\,{{\mathbf {e}}}_2\) are respectively tangent to the meridian and latitude of \(\,{{\mathbb {S}}}^2\) through \({{\mathbf {z}}}\in {{\mathbb {S}}}^2\), and so applying \(R_3(\phi )\) gives that the vectors \(R_{{\mathbf {z}}}{{\mathbf {e}}}_1\) and \( R_{{\mathbf {z}}}{{\mathbf {e}}}_2\) are respectively tangent to the meridian and latitude through \({{\mathbf {z}}}\) in the general case. Therefore the corresponding tangent spaces at \(Z={{\mathscr {V}}}({{\mathbf {z}}})\in {\mathscr {O}}\) are spanned by \({\mathrm D}{\mathscr {V}}({{\mathbf {z}}})R_{{\mathbf {z}}}{{\mathbf {e}}}_j\) for \(j=1,2\) respectively. The equivariance property (2.3) gives \({\mathrm D}{\mathscr {V}}(R{{\mathbf {z}}}) R={\widetilde{R}}{\mathrm D}{\mathscr {V}}({{\mathbf {z}}})\) for any \({{\mathbf {z}}}\in {{\mathbb {S}}}^2\) and \(R\in \mathrm{SO}(3)\), and so, as \({{\mathbf {z}}}=R_{{\mathbf {z}}}{{\mathbf {e}}}_3\),
for \(j=1,2\). It is immediate to check, using (2.4) and (2.12), that
and so applying \({\widetilde{R}}_{{\mathbf {z}}}\) gives the result. \(\quad \square \)
Corollary 2.5
\({\mathscr {T}}^Z=\mathrm{span}\{E_{11}^Z,E_{12}^Z\} = V_1^Z\). \(\quad \square \)
The latitude curve through \(Z=Z(\theta ,\phi )\in {\mathscr {O}}\) is the orbit of Z under the action of \(\Sigma _{{{\mathbf {e}}}_3}=\{R_3(\phi )\}_{\phi \in [\,0,2\pi )}\) and so its tangent at Z is spanned by \([W_3,Z\,]\). Indeed, we find that
which we shall make use of below.
From Corollary 2.5 it follows that the normal space \({\mathscr {N}}^Z\) to \({\mathscr {O}}\) at Z (the orthogonal complement in V to the tangent space \({\mathscr {T}}^Z\)) is given by
3 The Dynamical System After Perturbation
Since G is \(\mathrm{SO}(3)\)-equivariant and so in particular is equivariant with respect to the action of the isotropy subgroup \(\Sigma _{{\mathbf {z}}}\) on V, the fact that \(\Sigma _{{\mathbf {z}}}\) fixes Z means that the derivative \({\mathrm D}G(Z):V\rightarrow V\) respects the decomposition (2.8). Moreover, Assumption 2 and equivariance imply that G vanishes on the entire orbit \({\mathscr {O}}\) and so \({\mathrm D}G(Z)\) vanishes on \({\mathscr {T}}^Z=V_1^Z\).
Let \(\lambda \) denote the eigenvalue of \({\mathrm D}G(Z)\) on \(V_0^Z=\mathrm{span}\{Z\}\), which by equivariance is independent of \(Z\in {\mathscr {O}}\). Since \({\mathrm D}G(Z)\) commutes with the rotation action of \(\Sigma _{{\mathbf {z}}}\) on \(V_2^Z\) its two eigenvalues on \(V_2^Z\) are complex conjugates and again independent of Z; we assume them to be real (as they will be in the gradient case, of most interest to us) and denote them by \(\mu \) (repeated).
Assumption 3
\(\mu \in {{\mathbb {R}}}\) and \(\lambda \mu \ne 0\).
Even without the assumption \(\mu \in {{\mathbb {R}}}\) but with \(\lambda \) and \(\mathfrak {R}(\mu )\) both nonzero the manifold \({\mathscr {O}}\) is normally hyperbolic and therefore it persists as a unique nearby smooth flow-invariant manifold \({\mathscr {O}}(\beta )\) for (1.2) for sufficiently small \(|\beta |>0\); see [24, 42] for the general theory invoked here. Our interest is to discover which periodic orbits on \({\mathscr {O}}\) persist as periodic orbits after such a perturbation.
Remark 3.1
The same approach is used in [52, 53] to detect steady states (equilibria) bifurcating from more general group orbits. The geometry of the tangent and normal spaces to all orbits of \(\mathrm{SO}(3)\) in V is exploited there in a significant way, although using constructions slightly different from ours.
We now make explicit the assumption of linearity and frame-indifference of the contribution to (1.2) from the non-rotational component of the shear flow. The frame-indifference is natural for a physical model, while the linearity is generally assumed for simplicity; see for example [51] and compare equation (4) in [36].
Assumption 4
The term \(\varvec{L}({ Q})D\) is linear in D, and \(\varvec{L}({\widetilde{R}}{ Q}){\widetilde{R}}D={\widetilde{R}}\,\varvec{L}({ Q})D\) for all \({ Q}\in V\) and \(R\in \mathrm{SO}(3)\).
It is immediate to check that Assumption 4 holds for (1.5). As a consequence, we have the following elementary result:
Proposition 3.2
If \({ Q}\in V\) is fixed by the action of \(R\in \mathrm{SO}(3)\) then \({\widetilde{R}}\varvec{L}({ Q})D=\varvec{L}({ Q}){\widetilde{R}}D\). \(\quad \square \)
Corollary 3.3
Each term of \(F(\cdot ,\beta )\) maps \({\mathscr {N}}^*:={\mathscr {N}}^{{ Q}^*}\) into itself, and so the subspace \({\mathscr {N}}^*\) is invariant under the flow of \(F(\cdot ,\beta )\) for all \(\beta \).
Proof
Using (2.23) we see from Section 2.3 that \( {\mathscr {N}}^*\) is the fixed-point subspace for the action of \(R_3(\pi )\) on V. If \({ Q}\in {\mathscr {N}}^*\) then \(G({ Q})\in {\mathscr {N}}^*\) by equivariance, and \([W,Q\,]\in {\mathscr {N}}^*\) since \(W\in {\mathscr {N}}^*\). Also Proposition 3.2 gives \({\widetilde{R}}_3(\pi )\varvec{L}({ Q})D=\varvec{L}({ Q}){\widetilde{R}}_3(\pi )D =\varvec{L}({ Q})D\) and so \(\varvec{L}({ Q})D \in {\mathscr {N}}^*\). \(\quad \square \)
From the symmetry and Corollary 3.3 we have two immediate results: the north pole \({ Q}^*\) equilibrium (logrolling) and the equator \({{\mathscr {C}}}\) periodic orbit (tumbling) persist after perturbation.
Proposition 3.4
Let \(\omega \ne 0\) be fixed. For sufficiently small \(|\beta |\) there exist for (1.2)
-
(i)
a smooth family of equilibria \({ Q}^*\!(\beta )\) in \({\mathscr {N}}^*\) with \({ Q}^*\!(0)={ Q}^*\);
-
(ii)
a smooth family of periodic orbits \({{\mathscr {C}}}(\beta )\) in \({\mathscr {N}}^*\) with \({{\mathscr {C}}}(0)={{\mathscr {C}}}\) and with period tending to \(\pi /\omega \) as \(\beta \rightarrow 0\).
Proof
(i) The eigenvalues of \({\mathrm D}G({ Q}^*)\) are \(\lambda \), 0 (repeated) and \(\mu \) (repeated) with eigenspaces \(V_0^*,V_1^*,V_2^*\) respectively, and the corresponding eigenvalues of \({ Q}\mapsto \omega [W,{ Q}\,]\) are \(0,\pm \,{\mathrm i}\omega ,\pm \,2{\mathrm i}\omega \) by (2.9)–(2.11) and the remarks preceding. Hence the eigenvalues of \({\mathrm D}F({ Q}^*,0)\) are
and so by the Implicit Function Theorem there exists a smooth family of equilibria \({ Q}^*\!(\beta )\) with \({ Q}^*\!(0)={ Q}^*\) and with (for \(\beta \) fixed) \({ Q}^*\!(\beta )\) the only equilibrium close to \({ Q}^*\). Since \(F(\cdot ,\beta )\) maps \( {\mathscr {N}}^*\) to itself by Corollary 3.3, the Implicit Function Theorem restricted to \( {\mathscr {N}}^*\) implies that \({ Q}^*\!(\beta )\in {\mathscr {N}}^*\).
(ii) The equator \({{\mathscr {C}}}\) lies in \({\mathscr {O}}\cap {\mathscr {N}}^*\) and is an isolated periodic orbit in \({\mathscr {N}}^*\) with characteristic multipliers there \({\mathrm e}^{\pi \lambda /\omega }\) and \({\mathrm e}^{\pi \mu /\omega }\) (repeated). We seek a fixed point for the first-return map on a local Poincaré section. Since the multipliers differ from 1, the Implicit Function Theorem applied on \( {\mathscr {N}}^*\) gives the result. \(\quad \square \)
3.1 Rotated Coordinates
The effect of the perturbation \(\beta \varvec{L}({ Q})D\) on the system (1.2) when \(\beta \ne 0\) is most usefully understood in terms of a co-moving coordinate frame that rotates with the unperturbed system (\(\beta =0\)), since in these coordinates the rotation term \([W,{ Q}\,]\) vanishes (cf. [60, Section 2]). Explicitly, with \(W=W_3\) and the substitution
and writing for \(\tfrac{{\mathrm d}}{{\mathrm d}t}\) we have
and so, from (1.2),
that is
using \(\mathrm{SO}(3)\)-equivariance of \(G\,\); here, for any \({ Q}\in V\), we write
using Assumption 4 on frame-indifference of \(\varvec{L}({ Q})\). Thus in (3.1) and with \({ Q}_R\) again written as \({ Q}\) the rotation term \([W,{ Q}\,]\) has been removed from (1.2) at a cost of replacing D by the time-dependent term \({\widetilde{R}}_3(-\omega t)D\).
For given \(\beta \) we denote the flow of (1.2) by \(\varphi ^t(\cdot ,\beta ):V\rightarrow V\), and denote the time evolution map of the nonautonomous system (3.1) by
To simplify notation in what follows we choose \(t_0=0\) and write for \({ Q}\in V\)
Observe in particular that, for \(T_0=2\pi /\omega \),
3.2 Local Linearisation: the Fundamental Matrix
An important role will be played by the linear transformation (fundamental matrix)
that satisfies the local linearisation of (1.2) (also called the variational equation [49, Ch.VIII], [37, p.23]) along the \({\tilde{\varphi }}\)-orbit of \({ Q}\) when \(\beta =0\,\), namely
For \(Z={\mathscr {V}}({{\mathbf {z}}})\in {\mathscr {O}}\) we have \(G(Z)=0\) and so \({\tilde{\varphi }}^t(Z,0)=Z\) for all \(t\in {{\mathbb {R}}}\) when \(\beta =0\). The variational equation (3.5) for \({ Q}=Z\) thus becomes
where
is independent of t. Moreover, since \(A^Z\) is \(\Sigma _{{\mathbf {z}}}\)-equivariant, it has the decomposition
in terms of the linear projections \(p_i^Z:V\rightarrow V_i^Z\) for \(i=0,1,2\), and so
with respect to the same decomposition (2.8). In particular we have the following key fact.
Corollary 3.5
\(p_1^Z\,M(t,Z)=p_1^Z\) for \(Z\in {\mathscr {O}}\). \(\quad \square \)
In what follows we shall make much use of this result, which states that the tangent space \({\mathscr {T}}^Z=V_1^Z\) to \({\mathscr {O}}\) at Z consists of equilibria of the variational equation at Z.
4 The Poincaré Map
All points \(Z\in {\mathscr {O}}\) satisfy \(\varphi ^{T_0}(Z,0)=Z\) for \(T_0=2\pi /\omega \). Our aim is to discover which of these periodic orbits persist for sufficiently small \(|\beta |>0\), and to discern their stability. Systems of the form (3.1) (not necessarily with symmetry) have a long pedigree in the differential equations literature; in our application the symmetry plays a crucial role. The method we use is to apply Lyapunov–Schmidt reduction to a Poincaré map to obtain a 1-dimensional bifurcation function, and to look for its simple zeros when \(\beta \ne 0\): by standard arguments as in [5, 7, 10, 16, 32] for example, these correspond to persistent periodic orbits. The existence of zeros Z for small \(|\beta |\) is established by taking a series expansion of the bifurcation function in terms of \(\beta \) with coefficients functions of Z. Expressions for these coefficients in a general setting are given in [7], and in principle we could simply set out to evaluate these expressions in our case. However, in so doing we could lose sight of important geometric features of V that are fundamental to the shear flow problem, and therefore instead we re-derive the relevant terms explicitly in our symmetric setting.
4.1 Poincaré Section
Let \(Z=Z(\theta ,\phi )\in {\mathscr {O}}\) as in (2.7) with \(Z\ne { Q}^*\). Let \({{\mathscr {B}}}^*\) denote the orthonormal basis for V given by
where \(E_0\) and \(E_{ij}\) for \(i,j \in \{1,2\}\) are defined in (2.12) and (2.13). Let \({{\mathscr {B}}}^Z\) denote the rotated basis (also orthonormal)
with notation as in (2.16). From (2.23) the 3-dimensional normal space \({\mathscr {N}}^Z\) to \({\mathscr {O}}\) in V at \(Z\in {\mathscr {O}}\) is
so that \(V={\mathscr {T}}^Z\oplus {\mathscr {N}}^Z\) by Corollary 2.5, and so for sufficiently small \(\varepsilon _0>0\) the union
forms an open tubular neighbourhood of \({\mathscr {O}}\) in V, where \({\mathscr {N}}^Z_\varepsilon =\{{ Q}\in {{\mathscr {N}}}^Z:|{ Q}|<\varepsilon \}\).
To construct a Poincaré section for the flow of (1.2) we restrict Z to lie on a chosen meridian
on \({\mathscr {O}}\), so that
is a smooth 4-manifold that intersects \({\mathscr {O}}\) transversely along \({{\mathscr {M}}}\). Moreover, F(Z, 0) is nonzero and orthogonal to \({{\mathscr {U}}}^{\varepsilon _0}_{{\mathscr {M}}}\) for all \(Z\in {{\mathscr {M}}}{\setminus }{ Q}^*\) since from (1.2)
by Assumption 2 and (2.22), while Lemma 2.4 shows that \(E^Z_{12}\) is orthogonal to \({\mathscr {N}}^Z\) and to \({{\mathscr {M}}}\).
Thus \({{\mathscr {U}}}^{\varepsilon _0}_{{\mathscr {M}}}\) is a global (along \({{\mathscr {M}}}\)) Poincaré section for all the (periodic) orbits through \({{\mathscr {M}}}{\setminus }{ Q}^*\) generated by the unperturbed vector field \(F(\cdot ,0)\). The least period for \(Z\in {{\mathscr {M}}}{\setminus }{ Q}^*\) is \(T_0=2\pi /\omega \), with the exception that if Z lies on the equator \({{\mathscr {C}}}\) then the least period is \(T_0/2=\pi /\omega \). We next show that there exists \(0<\varepsilon \le \varepsilon _0\) such that the corresponding \({{\mathscr {U}}}^{\varepsilon }_{{\mathscr {M}}}\) is in an appropriate sense a Poincaré section for all orbits close to \({\mathscr {O}}\) generated by the perturbed vector field \(F(\cdot ,\beta )\) including those lying in \({ Q}^*+{\mathscr {N}}^*_\varepsilon \).
Proposition 4.1
Let \({{\mathscr {M}}}={{\mathscr {M}}}_{\phi _{\,0}}\) be a meridian of \({\mathscr {O}}\) with \({{\mathscr {U}}}^{\varepsilon _0}_{{\mathscr {M}}}\) a tubular neighbourhood of \({\mathscr {O}}\) restricted to \({{\mathscr {M}}}\) constructed using the normal bundle as in (4.4). Then there exists \(\beta _0>0\) and \(0<\varepsilon \le \varepsilon _0\) and a smooth function
such that if \({ Q}\in {{\mathscr {U}}}^{\varepsilon }_{{\mathscr {M}}}\) and \({ Q}\notin { Q}^*+{\mathscr {N}}^*_\varepsilon \) then the future (\(t\ge 0\)) trajectory of the system (1.2) from \({ Q}\) leaves \({{\mathscr {U}}}^{\varepsilon }_{{\mathscr {M}}}\) and remains in \({{\mathscr {U}}}^{\varepsilon _0}\), meeting \({{\mathscr {U}}}^{\varepsilon _0}_{{\mathscr {M}}}\) for the second time when \(t=T({ Q},\beta )\). Furthermore, \(T({ Q},\beta )\rightarrow T_0=2\pi /\omega \) as \(({ Q},\beta )\rightarrow ({ Q}^0,0)\) with \({ Q}^0\in {{\mathscr {M}}}\cup ({ Q}^*+{\mathscr {N}}^*_\varepsilon )\).
A key part of Proposition 4.1 is the smoothness of T on all of its domain including \(\bigl ({ Q}^*+{\mathscr {N}}^*_\varepsilon \bigr )\times (-\beta _0,\beta _0)\), since there \(F(\cdot ,\beta )\) lies in \({\mathscr {N}}^*\) by Corollary 3.3 and so T is not strictly a ‘time of second return’.
Proof
Let
where \(Z=Z(\theta ,\phi )\in {\mathscr {O}}\) as in (2.7) and \(U^Z\in {\mathscr {N}}^Z\) with \(U\in {\mathscr {N}}^*\). Then
using
for \(j=2,3\).
We show that there is a positive smooth function on a neighbourhood of \({{\mathscr {M}}}\) that coincides with \({\dot{\phi }}\) away from \({ Q}^*+{\mathscr {N}}^*_\varepsilon \), so that time t can in effect be replaced there by angle \(\phi \).
Writing
where \(u_i\in {{\mathbb {R}}},\, i=0,1,2\), we make use of the identities
as well as
Inspecting the terms on the right hand side of (4.5) we find, from (4.6), that
and, using (4.7),
Next, we take the inner product of (4.5) with \({\widetilde{E}}^Z:={\widetilde{R}}_{{\mathbf {z}}}{\widetilde{E}}\), where
orthogonal to the right hand side of (4.8) and to \(\dot{U}\in V_2^*\); since \({\widetilde{R}}_{{\mathbf {z}}}\) preserves inner products this annihilates the \({\dot{\theta }}\) and \(\dot{U}\) terms in (4.5) and leaves
where
with \(u=(u_0,u_1,u_2)\).
The next step is to replace \({\dot{{ Q}}}\) in (4.10) by the right hand side \(F({ Q},\beta )\) of (1.2). Since G respects the isotypic decomposition (2.8) we have by equivariance \(G(Z+U^Z)\in {\mathscr {N}}^Z\) and so
Also,
from the frame-indifference Assumption 4. Writing \({\widetilde{R}}_{{\mathbf {z}}}^{-1}D=D^0_T+D^0_N\) with \(D^0_T\in {\mathscr {T}}^*=V_1^*\) and \(D^0_N\in {\mathscr {N}}^*= V_0^*\oplus V_2^*\) we see from Corollary 3.3 that \(D^0_N\) makes zero contribution to (4.13), and so we focus on \(D^0_T\). We have by elementary matrix evaluation
since \(D=\sqrt{2} E_{22}\), while
hence
Therefore, from (4.13) and (4.16),
where
Substituting (4.11), (4.12) and (4.17) into (4.10) with \({\dot{{ Q}}} = F({ Q},\beta )\), we obtain
Taking \(\varepsilon >0\) small enough so that \(b(a,u)>0\) and dividing (4.19) through by \(b(a,u)\sin \theta \), for \(\beta \) sufficiently small we have \({\dot{\phi }}>\omega /2\) for \(\theta \ne 0\) and we observe that \({\dot{\phi }}\) extends smoothly to \(\theta =0\), corresponding to \({ Q}\in {\mathscr {N}}^*\).
Consequently in \((\theta ,\phi ,U)\) coordinates for sufficiently small \(|\beta |\) and |u| the flow has positive component in the \(\phi \) direction. Since \({\mathscr {O}}\) (given by \(u=0\)) in invariant under the flow of (1.2) when \(\beta =0\) and is given by \(\phi \)-rotation only, it follows that for \(\varepsilon \) and \(|\beta |\) sufficiently small and \({ Q}=Z+U^Z\in {{\mathscr {U}}}^{\varepsilon }\) we can define \(T({ Q},\beta )\) to be the time-lapse from \(\phi ={\phi }_{0}\) to \(\phi =\phi _{\,0}+2\pi \) if \(Z\ne { Q}^*\) and to be \(T_0=2\pi /\omega \) when \(Z={ Q}^*\). \(\quad \square \)
Now we are able to define a Poincaré map close to \({\mathscr {O}}\) and for sufficiently small \(|\beta |\).
Definition 4.2
The Poincaré map \(P: {{\mathscr {U}}}^{\varepsilon }_{{\mathscr {M}}}\times {{\mathbb {R}}}\rightarrow {{\mathscr {U}}}^{\varepsilon _0}_{{\mathscr {M}}}\) is given by
where \(T({ Q},\beta )\) is as defined in Proposition 4.1.
By construction, every \({ Q}\in {{\mathscr {U}}}^{\varepsilon }_{{\mathscr {M}}}\) lies in \(Z+{\mathscr {N}}^Z\) for some \(Z=Z(\theta ,\phi )\), where \(\phi \) is unique \(\bmod \,2\pi \) provided \(\theta \ne 0\), that is \(Z\ne { Q}^*\). Denoting \(\phi =m({ Q})\) we can characterise \(T({ Q},\beta )\) for \({ Q}\notin { Q}^*+{{\mathscr {N}}}_\varepsilon ^*\) as the unique value of t close to \(T_0=2\pi /\omega \) such that
The bifurcation analysis that follows proceeds by expanding \(P({ Q},\beta )\) in terms of the perturbation parameter \(\beta \).
4.2 First Order \(\beta \)-Derivatives
Differentiating (4.20) with respect to \(\beta \) gives
where here and throughout we use \({}'\) to denote differentiation with respect to the second component \(\beta \). At \(({ Q},\beta )=(Z,0)\) the expression (4.22) becomes
using (3.3). We now turn attention to evaluating \(T'(Z,0)\).
Differentiating (4.21) with respect to \(\beta \) at \(({ Q},\beta )=(Z,0), Z\ne Q^*\) gives
By construction \( m({ Q})= m(Z)\) for all \({ Q}\in Z+{\mathscr {N}}^Z\) and therefore \({\mathrm D}m(Z)\) annihilates \({\mathscr {N}}^Z\). Recall from Lemma 2.4 that the tangent space to \({{\mathscr {M}}}\) at Z is spanned by \(E_{11}^Z(0)\) while the tangent space to the latitude curve through Z is spanned by \(E_{12}^Z(\pi /2)\). It follows that the derivative \({\mathrm D}m(Z):V\rightarrow {{\mathbb {R}}}\) annihilates \(E_{11}^Z(0)\) and is an isomorphism from \(\mathrm{span}\{E_{12}^Z(\pi /2)\}\) to \({{\mathbb {R}}}\), so that, in particular,
since, from (2.22), we see that
We next introduce a variable that plays a central role in subsequent calculations.
Definition 4.3
\(y(t,{ Q}):=\bigl ({\tilde{\varphi }}^t\bigr )'({ Q},0)\).
From (3.3) we see, in particular, that
With this notation we can write (4.24) as
A consequence of Assumption 4 is that the second term in (4.28) vanishes.
Lemma 4.4
\({\mathrm D}m(Z)y(T_0,Z)=0\).
Proof
Substituting \(Q_R={\tilde{\varphi }}^t(Q,\beta )\) into (3.1) and differentiating with respect to \(\beta \) at \(\beta =0\) shows that \(y(t,{ Q})\) satisfies the differential equation
with \(y(0,{ Q})=0\) and \({\widetilde{\varvec{L}}}(t,{ Q})D\) as in (3.2). Solving this equation by the usual variation of constants formula [37] we obtain
in terms of the fundamental matrix \(M(t,{ Q})\) as in (3.4), and so, in particular, for each \(Z\in {\mathscr {O}}\),
using (3.9). Hence
as is clear from (3.2). Thus \(y(T_0,Z)\in {\mathscr {N}}^Z\) and so \({\mathrm D}m(Z) y(T_0,Z)=0\) and the lemma is proved. \(\quad \square \)
In view of Lemma 4.4 the expression (4.24) becomes
and hence, from (4.25), we arrive at the following key result:
Proposition 4.5
\(T'(Z,0)=0\) for all \(Z\in {\mathscr {O}}{\setminus }{ Q}^*\), and so by continuity for all \(Z={\mathscr {O}}\) . \(\quad \square \)
The analogous result holds for the \({ Q}\)-derivative \({\mathrm D}T({ Q},\beta )\) at (Z, 0).
Proposition 4.6
\({\mathrm D}T(Z,0)=0\) for all \(Z\in {\mathscr {O}}.\)
Proof
Here differentiating (4.21) with respect to \({ Q}\) at \(({ Q},\beta )=(Z,0),Z\ne Q^*\) gives
for \(H\in V\), that is,
from (3.4) and (3.7). Since \(e^{T_0A^Z}\) respects the splitting \(V={\mathscr {T}}^Z\oplus {\mathscr {N}}^Z\) (see (3.9)) and \({\mathrm D}m(Z)\) annihilates \({\mathscr {N}}^Z\) we deduce \({\mathrm D}T(Z,0)H=0\) for \(H\in {\mathscr {N}}^Z\) using (4.25), while if \(H\in {\mathscr {T}}^Z\) then \({\mathrm e}^{T_0 A^Z}H=H\) and so also \({\mathrm D}T(Z,0)H=0\). The result follows for \(Z=Q^*\) by continuity. \(\quad \square \)
5 Lyapunov–Schmidt Reduction
Our aim in this section is to seek solutions \({ Q}={ Q}(\beta )\in {{\mathscr {U}}}^{\varepsilon }_{{\mathscr {M}}}\) for sufficiently small \(|\beta |>0\) to the equation
where \(P: {{\mathscr {U}}}^{\varepsilon }_{{\mathscr {M}}}\times {{\mathbb {R}}}\rightarrow {{\mathscr {U}}}^{\varepsilon _0}_{{\mathscr {M}}}\) is as in (4.20), and to determine the stability of the \(T({ Q}(\beta ),\beta )\)-periodic orbit of (1.2) that each of these represents. Of particular interest are out-of-plane solutions, corresponding to kayaking orbits. We apply Lyapunov–Schmidt reduction to (5.1) along \({{\mathscr {M}}}\) exploiting the \(\mathrm{SO}(3)\)-invariant tangent and normal structure to \({\mathscr {O}}\).
Lyapunov–Schmidt reduction is a fundamental tool in bifurcation theory, and amounts to a simple application of the Implicit Function Theorem. Accounts can be found in many texts such as [2, Sect. 5.3], [9, Sect. 4.4] , [16, Sect. 2.4], [32, Sect. I§3], [44, Sect. I.2], [45, Sect. 2.2], [73, Sect. 3.1] and surveys [11, 38, 57]. Although the method is local in origin, it can be applied globally on a manifold on which a given vector field vanishes, or on which given map** is the identity, by piecing together local constructions and invoking the uniqueness clause of the Implicit Function Theorem. This is the version we use here, which fits into the general framework of [5, 7, 50] and has significant overlap with the geometric methods of [52, 53].
Let \({ Q}\in {\mathscr {N}}^Z\). Then \({ Q}_N =Q\) and \({ Q}_T =0\) where the suffices N, T will denote projections to \({\mathscr {N}}^Z,{\mathscr {T}}^Z\) respectively. Hence (5.1) is equivalent to the pair of equations
When \(\beta =0\) the equation (5.2) is satisfied by \({ Q}=Z\), and by (3.9) the \({ Q}\)-derivative
has eigenvalues \(\{e^{\lambda T_0},e^{\mu T_0},e^{\mu T_0}\}\) with \(\lambda ,\mu \) both nonzero, so
is an isomorphism. It follows by the Implicit Function Theorem and the (smooth) local triviality of the normal bundle, as well as the compactness of \({{\mathscr {M}}}\), that for all sufficiently small \(|\beta |\) there exists a smooth section
of the normal bundle of \({\mathscr {O}}\) restricted to \({{\mathscr {M}}}\) such that for sufficiently small \(|\beta |\) the map
has the property that
for all \(Z\in {{\mathscr {M}}}\), with \(\sigma (Z,0)=0\).
It therefore remains to solve the equation (5.3) along \({{\mathscr {M}}}\) given (5.4), that is to solve the reduced equation or bifurcation equation
for \((Z,\beta )\in {{\mathscr {M}}}\times {{\mathbb {R}}}\) and for \(|\beta |\) sufficiently small. Since \({\mathscr {T}}^Z=V_1^Z=\mathrm{span}\{E_{11}^Z,E_{12}^Z\}\) and by construction the Poincaré map P has no component in the direction of the vector field \(E_{12}\), the bifurcation equation (5.5) can by Lemma 2.4 be written more specifically as
with \(P_{11}=p_{11}^ZP\), where \(p_{11}^Z\) denotes projection to \(\mathrm{span}\{E_{11}^Z\}\). We thus seek the zeros of the bifurcation function \({{\mathscr {F}}}(\cdot ,\beta ):{{\mathscr {M}}}\rightarrow {{\mathbb {R}}}\) where
for sufficiently small \(|\beta |>0\). We shall find these by taking a perturbation expansion of \({{\mathscr {F}}}(Z,\beta )\) in terms of \(\beta \).
5.1 Perturbation Expansion of the Bifurcation Function
First, we need a \(\beta \)-expansion of the Poincaré map P which we write as
for \(Q\in {\mathscr {N}}^Z, Z\in {{\mathscr {M}}}\). We also make use of the ‘approximate’ Poincaré map
with \(\beta \)-expansion
noting that \(\tilde{P}(Z,0) =P(Z,0)\) by (3.3). Although \(\tilde{P}\) is not the same as P, the next result shows that up to second order in \(\beta \) at \({ Q}=Z \in {\mathscr {O}}\) it differs from P only in the direction of the unperturbed vector field F(Z, 0).
Proposition 5.1
for \(i=0,1\), and
Proof
Of course \(P^{\,0}(Z)=\tilde{P}^{\,0}(Z) = Z\), and from (4.23) we have \(P^1(Z)=\tilde{P}^1(Z)\) since \(T'(Z,0)=0\) by Proposition 4.5. Next, differentiating (4.22) with respect to \(\beta \) at \(({ Q},\beta )=(Z,0)\) we obtain
again using (twice) the fact that \(T'(Z,0)=0\). \(\quad \square \)
In expanding \(P(Z+\sigma (Z,\beta ),\beta )\) we shall require the first and second \({ Q}\)-derivatives \({\mathrm D}P({ Q},\beta )\) and \({\mathrm D}^2P({ Q},\beta )\) of P at \(({ Q},\beta )=(Z,0)\). Recall that the tangent space to \({{\mathscr {U}}}_{{\mathscr {M}}}\) at \(Z\in {{\mathscr {M}}}\) is \(F(Z,0)^\perp =\mathrm{span}\{E_{11}^Z\}\oplus {\mathscr {N}}^Z\).
Proposition 5.2
while for \(H,K\in F(Z,0)^\perp \),
and
Proof
For \(H\in F(Z,0)^\perp \) we have
which, at \(({ Q},\beta )=(Z,0)\), becomes
giving (5.11) in view of Proposition 4.6. The expression (5.14) shows that \({\mathrm D}P\) and \({\mathrm D}\varphi ^t|_{t=T({ Q},\beta )}\) differ by a scalar multiple of \(F(P({ Q},\beta ),\beta )\), and moreover this scalar multiple \({\mathrm D}T(Q,\beta )H\) vanishes when \(({ Q},\beta )=(Z,0)\) by Proposition 4.6. Hence on one further differentiation both the \({ Q}\)-derivative and the \(\beta \)-derivative of \({\mathrm D}P\) at (Z, 0) differ from those of \({\mathrm D}\varphi ^t|_{t=T(Z,0)}= {\mathrm D}{\tilde{\varphi }}^{T_0}={\mathrm D}\tilde{P}\) only by a scalar multiple of F(Z, 0). Therefore \({\mathrm D}^2P^{\,0}(Z)\) and \({\mathrm D}P^1(Z)\) differ from \({\mathrm D}^2\tilde{P}^{\,0}(Z)\) and \({\mathrm D}\tilde{P}^1(Z)\) respectively by scalar multiples of F(Z, 0). \(\quad \square \)
5.2 First Order Term of the Bifurcation Function
Here we denote
as in (5.7), and likewise for the second derivatives.
Proposition 5.3
\( P_{11}'(Z,0)= 0. \)
Proof
Differentiating (5.6) with respect to \(\beta \) at \(\beta =0\) gives
using (3.4) and Proposition 5.1 for \(i=0,1\). Now
by Corollary 3.5 and \(p^Z_{11}\sigma '(Z,0)=0\) since \(\sigma '(Z,0)\in {\mathscr {N}}^Z\). Also \(\tilde{P}^1(Z) = y(T_0,Z)\) as in (4.27), and \(p^Z_{11} y(T_0,Z)=0\) from (4.32). Thus both terms on the right hand side of (5.16) vanish. \(\quad \square \)
A geometric interpretation of Proposition 5.3 is that to first order in \(\beta \) the \(\mathrm{SO}(3)\)-orbit \({\mathscr {O}}\), on which every dynamical orbit (other than the fixed point \(Q^*\)) is \(2\pi /\omega \) periodic, perturbs to an invariant manifold with the same dynamical property, so that neutral stability of all periodic orbits is preserved.
5.3 Second Order Term of the Bifurcation Function
Given that the first order term in the \(\beta \)-expansion of \({{\mathscr {F}}}(Z,\beta )\) vanishes by Proposition 5.3 we turn to the second order term. Differentiating \(P_{11}(Z,\beta )\) twice with respect to \(\beta \) at \(\beta =0\) we obtain from the left hand side of (5.6)
where we write \(P^{\,i}_{11}\) for \(p^Z_{11}P^{\,i}, i=0,1,2\).
Remark 5.4
The expression (5.18) is a particular case of the formula for the second order term of the bifurcation function in a general setting derived in [7, Appendix A].
To evaluate (5.18) a significant simplification can be made.
Proposition 5.5
P may be replaced by \(\tilde{P}\) in all terms on the right hand side of (5.18).
Proof
By Propositions 5.1 and 5.2 each term differs from its counterpart with \(\tilde{P}\) by a scalar multiple of F(Z, 0), which is annihilated by \(p_{11}^Z\). \(\quad \square \)
We next investigate in turn each of the terms of (5.18) with \(\tilde{P}\) in place of P.
5.3.1 First \({ Q}\)-Derivative of \(\tilde{P}^{\,0}\)
As \(\sigma (Z,\beta )\in {\mathscr {N}}^Z\) its \(\beta \)-derivatives also lie in \({\mathscr {N}}^Z\), and with \({\mathrm D}\tilde{P}^{\,0}(Z)=M(T_0,Z)\) it follows from (5.17) that
5.3.2 Second \({ Q}\)-Derivative of \(\tilde{P}^{\,0}\)
Expanding
so that in particular \({\tilde{\varphi }}_0^t({ Q})={\tilde{\varphi }}^t({ Q},0)\), we see from (3.1) with \(\beta =0\) that \({\mathrm D}^2{\tilde{\varphi }}_0^t({ Q})\) satisfies the equation
and so we obtain from the variation of constants formula and (3.4)
Since \(\sigma '(Z,0)\in {\mathscr {N}}^Z\) and so by (3.9) also \( M(s,Z)\sigma '(Z,0)\in {\mathscr {N}}^Z=V_0^Z\oplus V_2^Z \) we have
using Corollary 3.5 and the bilinear property of \(D^2G(Z)\) given in Proposition A.7.1.
5.3.3 First \({ Q}\)-Derivative of \(\tilde{P}^1\)
By definition of the solution to (3.1) through \({ Q}\) at \(t=0\) we have
Differentiating with respect to \(\beta \) at \(\beta =0\) we obtain
Differentiating (5.24) now with respect to \({ Q}\) at \({ Q}=Z\) gives, for \(H\in V\),
with notation
and \(A^Z={\mathrm D}G(Z)\) as in (3.8). Now \(\tilde{P}^1({ Q})={\tilde{\varphi }}_1^{T_0}({ Q})\) while \({\mathrm D}{\tilde{\varphi }}_0^t(Z)=e^{tA^Z}\) and \({\tilde{\varphi }}_1^t(Z)=y(t,Z)\) by Definition 4.3, so the variation of constants formula gives
To evaluate the term involving \({\mathrm D}\tilde{P}_1\) in (5.18) we must next substitute \(H=\sigma '(Z,0)\in {\mathscr {N}}^Z\) into (5.27). We write
to emphasise the tangent and normal character of these projections.
Proposition 5.6
where \(A_N^Z:=p_N^ZA^Z|_{{\mathscr {N}}^Z}\) (that is the \({\mathscr {N}}^Z\)-block of \(A^Z\)) and \(y_N(t,Z):=p_N^Zy(t,Z)\) with y(t, Z) as in Definition 4.3.
Proof
Differentiating (5.4) with respect to \(\beta \) at \(\beta =0\) yields
by (3.9) and Proposition 5.2. This gives the result since \(P'(Z,0)=\bigl ({\tilde{\varphi }}^{T_0}\bigr )'=y(T_0,Z)\) using Proposition 5.1 for \(i=1\). \(\quad \square \)
Now substituting (5.29) for H into (5.27) and again making use of Proposition A.7.1 gives
where \(y_T(t,Z):=p_T^Zy(t,Z)\) and \(B^Z_{11}:=p_{11}^ZB^Z\).
Finally, to complete the evaluation of (5.18) we make explicit the term involving \(\tilde{P}^2(Z)\) in that equation.
5.3.4 The Term \(\tilde{P}^2(Z)\)
An expression for \(\tilde{P}^2(Z)\) is obtained by differentiating (5.23) twice with respect to \(\beta \) at \(({ Q},\beta )=(Z,0)\). We find
and so a second differentiation at \(({ Q},\beta )=(Z,0)\) with \({\tilde{\varphi }}_1(Z) ={\tilde{\varphi }}'(Z,0)\) and \({\tilde{\varphi }}_2(Z) =\frac{1}{2} {\tilde{\varphi }}''(Z,\beta )|_{\beta =0}\) gives
Since \(\tilde{P}^2(Z)={\tilde{\varphi }}^{T_0}_2(Z)\) the variation of constants formula yields the expression
(cf. [50, \(f_2(z)\) on p.577]) where \(M(t,Z)=e^{tA_N^Z}\) and y(t, Z) is as in (4.30). Then
from Corollary 3.5 and the bilinearity property (A.8).
From (5.18) with (5.19), (5.22) and Proposition 5.3 we therefore arrive at the following conclusion:
Proposition 5.7
We have
where
with the terms on the right hand side given by the expressions (5.31) and (5.32).
\(\square \)
Observe that (5.34) can be simplified using (5.31), (5.32) and bilinearity of \(B^Z\). Denoting
and decomposing as usual \(\chi =\chi _N+\chi _T\) with the obvious notation we can re-express (5.34) as
The bifurcation function \({{\mathscr {F}}}(\cdot ,\beta )\) in (5.7) satisfies \({{\mathscr {F}}}'(Z,0)=0\) from Proposition 5.3 and
with \(F_2(Z)\) given by (5.36).
6 Explicit Calculation of the Bifurcation Function
For explicit calculation of the second order term \({{\mathscr {F}}}''(Z,0)\) we now take \(Z=Z(\theta ,\phi )\) and express the bifurcation function (5.7) in terms of \(\theta \) and \(\phi \). The choice of \(\phi \) is arbitrary so we expect the existence and stability results for periodic orbits to be independent of \(\phi \), but nevertheless we retain \(\phi \) at this stage as a check on the calculations.
Up to this point our analysis has assumed little more than the \(\mathrm{SO}(3)\)-equivariance (that is, frame-indifference) of the vector field G and the perturbation term \(\varvec{L}({ Q})D\) in the system (1.2) and the fact that \({ Q}^*\) is an equilibrium for the unperturbed (\(\beta =0\)) system. To proceed further and evaluate \(F_2(Z)\) we now need to make an explicit choice for the form of \(\varvec{L}({ Q})D\).
6.1 Choices for the Perturbing Field \(\varvec{L}({ Q})D\)
We consider in turn the three terms comprising the field \(\varvec{L}({ Q})D\) in (1.5), that is
-
(i)
\(\varvec{L}^c({ Q})D=D\)
-
(ii)
\(\varvec{L}^l({ Q})D =[D,{ Q}\,]^+\)
-
(iii)
\(\varvec{L}^q{ Q})(D)=\mathrm{tr}(D{ Q}){ Q}\),
where D as in (2.1) represents the symmetric part of the shear velocity gradient and we recall the notation (1.4). From (2.14) we obtain
Lemma 6.1
In the co-moving coordinate frame as in Section 3.1 the perturbation terms become respectively
-
(i)
\({\widetilde{\varvec{L}}}^c(t,{ Q})D:={\widetilde{R}}_3(-\omega t) D = \sqrt{2} E_2(\tfrac{\pi }{4}-\omega t)\)
-
(ii)
\({\widetilde{\varvec{L}}}^l(t,{ Q})D:={\widetilde{R}}_3(-\omega t) [D,{\widetilde{R}}_3(\omega t){ Q}\,]^+ =\sqrt{2} [ E_2(\tfrac{\pi }{4}-\omega t),{ Q}\,]^+\)
-
(iii)
\({\widetilde{\varvec{L}}}^q(t,{ Q})D:=\mathrm{tr}(D\,{\widetilde{R}}_3(\omega t){ Q}){ Q}=\mathrm{tr}({\widetilde{R}}_3(-\omega t)D\,{ Q}){ Q}=\sqrt{2}\,\mathrm{tr}(E_2(\tfrac{\pi }{4}-\omega t)Q)Q.\) \(\quad \square \)
Taking the derivative with respect to the \({ Q}\) variable we obtain
Proposition 6.2
In the respective cases (i),(ii),(iii) for \({ Q},H\in V\)
-
(i)
\({\mathrm D}{\widetilde{\varvec{L}}}^c(t,{ Q})D=0\)
-
(ii)
\(\big ({\mathrm D}{\widetilde{\varvec{L}}}^l(t,{ Q})H\big )D=\sqrt{2}\,[E_2(\tfrac{\pi }{4}-\omega t),H]^+\)
-
(iii)
\(\big ({\mathrm D}{\widetilde{\varvec{L}}}^q(t,{ Q})H\big )D =\sqrt{2}\, \mathrm{tr}(E_2(\tfrac{\pi }{4}-\omega t)H){ Q}+ \sqrt{2}\,\mathrm{tr}(E_2(\tfrac{\pi }{4}-\omega t){ Q})H.\) \(\quad \square \)
We next need expressions for the components of \(E_2(\pi /4-\omega t)\) in the basis \({{\mathscr {B}}}^Z\) as in (4.2). These could formally be found using \(5\times 5\) Wigner rotation matrices describing the action of \(\mathrm{SO}(3)\) on V as in physics texts such as [68], but in our case it will be simpler to calculate directly.
6.2 Expression of \(E_2(\pi /4-\omega t)\) in the Vector Basis \({{\mathscr {B}}}^Z\)
For any \(E_2(u)\) and any \(Z=Z(\theta ,\phi )\in {\mathscr {O}}\) and \({ Q}\in V\) we have, from (2.14),
Calculating \({\widetilde{R}}_2(\theta ){ Q}\) for \({ Q}=E_0,E_1(\alpha ),E_2(\alpha )\) in turn we find by elementary matrix multiplication
while
and
Using (6.1) and elementary computation we obtain the following results needed to compute the coefficients of \({\widetilde{\varvec{L}}}(t,{ Q})D\) in the basis \({\mathscr {B}}^Z\) at \(Z\in {\mathscr {O}}\):
Proposition 6.3
while
and
\(\square \)
Using Proposition 6.3 we see that \(E_2(\pi /4-\omega t)\) is expressed in terms of the orthonormal basis \({{\mathscr {B}}}^Z\) as follows:
Corollary 6.4
where the coefficients \(c_{01}^Z\) etc. depending on \((t,\theta ,\phi )\) are given by
and where
\(\square \)
6.3 Calculation of y(t, Z)
Armed with these coefficients we are now in a position to calculate y(t, Z) and subsequently \(\chi (t,Z)\), needed in order to evaluate (5.36). We consider in turn the three cases (i),(ii) and (iii) of Section 6.1, denoting the corresponding y by \(y^c,y^l,y^q\), respectively.
Case (i): \({\widetilde{\varvec{L}}}(t,{ Q})D={\widetilde{\varvec{L}}}^c(t,{ Q})D= \sqrt{2} E_2(\tfrac{\pi }{4}-\omega t)\)
From (4.30) and using (3.9) we have
For convenience we now introduce the polar coordinate notation
for \(\nu =\lambda ,\mu \), as well as the abbreviations
with the limiting cases
The cases when \(t=T_0=2\pi /\omega \) will also be important:
Using these we obtain from Corollary 6.4 the following expression for \(y^c(t,Z)\) in terms of the basis \({{\mathscr {B}}}^Z\):
Proposition 6.5
We have
where
Proof
and
The calculations for \(y_{12}^c,y_{21}^c\) and \(y_{22}^c\) are very similar. \(\square \)
Case (ii): \({\widetilde{\varvec{L}}} (t,{ Q})D={\widetilde{\varvec{L}}}^l(t,{ Q})D=\sqrt{2} [E_2(\tfrac{\pi }{4}-\omega t),{ Q}\,]^+\)
since Proposition A.2 shows that \({\widetilde{\varvec{L}}}^l(t,Z)D\) differs from \({\widetilde{\varvec{L}}}^c(t,Z)D\) only in that the coefficients of \(E_0^Z,E_1^Z(\alpha ),E_2^Z(\alpha )\) are multiplied by \(2a,a,-2a\) respectively. Hence in this case the result is the following:
Proposition 6.6
The components of \(y^l\) are given by
where \(y_i\) denotes \(p_i^Zy,\, i=0,1,2\). \(\quad \square \)
Case (iii): \({\widetilde{\varvec{L}}}(t,{ Q})D={\widetilde{\varvec{L}}}^q(t,{ Q})D= \sqrt{2} \mathrm{tr}(E_2(\tfrac{\pi }{4}-\omega t)Q)\,Q\)
In this case
using (6.5), and so
where
from (6.19). Thus
6.4 Calculation of \(\chi (t,Z)\)
From (5.29) and (5.35) we have
where we recall \(y_N=y_0+y_2\). Again we consider in turn the cases (i),(ii) and (iii), using respective notation \(\chi ^c,\chi ^l,\chi ^q\).
Case (i): \({\widetilde{\varvec{L}}}^c(t,{ Q})D= \sqrt{2} E_2(\pi /4-\omega t)\)
Here
and using Proposition 6.5 with (6.13) and (6.17) we find
giving
Likewise
which gives using (6.14) and (6.18) as well
while the definition (5.35) gives
from Proposition 6.5.
Case (ii): \({\widetilde{\varvec{L}}}^l(t,{ Q})D=\sqrt{2}[E_2(\pi /4-\omega t),{ Q}\,]^+\)
Since \(\chi \) is linear in y (see (6.28)) we immediately deduce from Proposition 6.6 the relations
Case (iii): \({\widetilde{\varvec{L}}}^q(t,{ Q})D=\sqrt{2}\mathrm{tr}(E_2(\pi /4-\omega t)Q)\,Q\)
Again since \(\chi \) is linear in y it follows from (6.26) that
6.5 The Bifurcation Function
We are now ready to calculate the terms appearing in the expression (5.36) that determine the bifurcation function. With \(y_T=y_1\) and \(\chi _N=\chi _0+\chi _2\) the first term is
We evaluate this initially for \(\chi _N^c,y_1^c\) and then use (6.21),(6.26),(6.33) and (6.34) to evaluate (6.35) with
using the bilinearity of \(B^Z\). Substituting \(\chi _0^c(t,Z)\) from (6.29) and using Proposition 6.5 and Corollary A.11, we find that
since, by (6.15),
and \(\sin 2\gamma _\lambda =2\omega /r_\lambda \) as in (6.12). Here we have introduced the notation
for \(\nu =\lambda ,\mu \).
Likewise, from (6.31), with Proposition 6.5 and Corollary A.11, we have
using
Observe that as anticipated the expressions (6.38) and (6.39) do not depend on the meridianal angle \(\phi \).
We now turn to the second term appearing in the expression (5.36) for the bifurcation function, namely
For Case (i) with \(\varvec{L}=\varvec{L}^c\) of course \({\mathrm D}\varvec{L}^c=0\) and so we focus on Case (ii) with \(\varvec{L}=\varvec{L}^l\). Proposition 6.2 (ii) and Corollary 6.4 together with Proposition A.8 give
where \(\chi _{01}=\chi _{01}(t,Z)\) etc. denote the coefficients of \(\chi (t,Z)\) in the basis \({{\mathscr {B}}}^Z\). We now take \(\chi =\chi ^c\) and evaluate (6.40) by integrating (6.41) from \(t=0\) to \(t=T_0\). Straightforward trigonometrical integrals using (6.29) and Corollary 6.4 give
since \(\lambda = r_\lambda \cos 2\gamma _\lambda \). Moreover, by (6.32) and Corollary 6.4
and also,
while from (6.31),
Similarly, we find
and
Thus (6.41) and (6.42)–(6.47) give
Using the above calculations, we can now evaluate the bifurcation function for the term \(\varvec{L}({ Q})D\) as a linear combination (1.5) of Cases (i),(ii),(iii). The corresponding y term has the form
with \(y^c\),\(y^l\) and \(y^q\) as in Proposition 6.5 with (6.21) and (6.23), (6.25), respectively, while
with the relevant components given by (6.29), (6.31), (6.32) for \(\chi ^c\), by (6.33) for \(\chi ^l\) and by (6.34) for \(\chi ^q\).
First take the restricted case \( m_q=0\). Here we find, from (5.36), that
since \({\mathrm D}{\widetilde{\varvec{L}}}^c(t,Z)=0\). Writing the bifurcation function \({{\mathscr {F}}}(Z,\beta )\) in coordinates as
so that
and here drop** the redundant variable \(\phi \), we observe from (6.38) and (6.39) (for \(B^Z\)) and (6.48) (for \({\mathrm D}{\widetilde{\varvec{L}}}\)) that each term in \(f_2(\theta )\) is a linear combination of the two terms:
The notation here reflects the fact that it is only the components \(\chi _0\) and \(\chi _2\) of \(\chi \) that play any role here.
The coefficients of these arising from the various terms that appear in (6.51) are as follows:

There collecting up terms in (6.51) gives
where
Now consider terms involving \( m_q\), not yet included. Since \(y_1^q=0\) from (6.26) and \(\chi _N^q=\chi _0^q\) from (6.34) the only terms that arise from \(B^Z\) are
from (6.38), and likewise, from (6.21),
Regarding terms arising from \({\mathrm D}{\widetilde{\varvec{L}}}\), we have, from (6.41) and (6.34), that
and so
using (6.42). Observe also that from Proposition 6.2 (iii) and (6.5), and (6.32),
as in (6.43), and so, likewise,
and also
because \(\chi _{11}^q=0\). Thus the contribution to \(F_2(Z)\) arising from the \({\mathrm D}{\widetilde{\varvec{L}}}\) term in (5.36) depends only on the linear (in \({ Q}\)) contribution \(\varvec{L}^l({ Q})D\).
Therefore the contribution of the \( m_q\)-term in \(\varvec{L}({ Q})D\) is merely to replace \(\tilde{\varLambda }_i\) in (6.56) by \(\varLambda _i\) for \(i=0,2\) where
and \(\varLambda _2=\tilde{\varLambda }_2\), the \( m_l m_q\) terms from (6.59) and (6.61) fortuitously cancelling.
7 Zeros of the Bifurcation Function, Periodic Orbits and Stability
Since, from (6.9),
the expression (6.55) using \(\varLambda _0,\varLambda _2\) becomes \(f_2(\theta )=\frac{T_0}{12\sqrt{2} a}\sin 2\theta {\widehat{f}}_2(\theta )\), where
with \(\tau _\lambda ,\tau _\mu \) both nonzero by Assumption 3.
Proposition 7.1
Solutions \(\theta \in [0,\pi )\) to \(f_2(\theta )=0\) are given by
and by solutions \(\theta \) to
that is (assuming \(\varLambda _2\ne 0\)),
\(\square \)
If \(\varLambda _2=0\) then solutions \(\theta \ne 0,\frac{\pi }{2}\in [0,\pi )\) to (7.6) exist only if also \(\varLambda _0=0\) in which case \(f_2(\theta )\) vanishes identically. However, if \(\varLambda _0=\varLambda _2=0\), then
where \((\xi ,\eta )=( m_c/ m_q, m_l/ m_q)\), supposing \( m_q\ne 0\) (otherwise \(\varLambda _0=\varLambda _2=0\) implies \( m_c= m_l=0\) also). Subtracting gives \(3\xi = -4\eta ^2\) and so the first equation factors into \(\xi =0\) (so \(\eta =0\)) or
giving \((\xi ,\eta ) = (-3a^2,-3a/2)\) or \((-12a^2,3a)\). Thus \(\varLambda _0=\varLambda _2=0\) just when \(( m_c: m_l: m_q)=(0:0: m_q)\) or \((-12a^2:3a:1)\) or \((6a^2:3a:-2)\); we exclude these possibilities.
Therefore assuming \(\varLambda _2\ne 0\) there exist solutions \(\theta \ne 0,\pi /2\in [0,\pi )\) to (7.7) if and only if \(3\frac{\varLambda _0}{\varLambda _2}\frac{\tau _\lambda }{\tau _\mu } + 1 > 4\), that is \(\frac{\varLambda _0}{\varLambda _2}\frac{\tau _\lambda }{\tau _\mu }>1\). Hence we have
Corollary 7.2
The second order term \(f_2(\theta )\) of the bifurcation function has no zeros \(\theta \ne 0,\pi /2\in [0,\pi )\) if \(\frac{\varLambda _0}{\varLambda _2}\frac{\tau _\lambda }{\tau _\mu }\le 1\), while if \(\frac{\varLambda _0}{\varLambda _2}\frac{\tau _\lambda }{\tau _\mu }>1\) there are two zeros \(\theta =\pi /2\pm \varTheta \) with \(\varTheta \rightarrow 0\) as \(\frac{\varLambda _0}{\varLambda _2}\frac{\tau _\lambda }{\tau _\mu }\rightarrow 1\). \(\quad \square \)
In the specific case of the Beris–Edwards model (1.2) with \(\varvec{L}({ Q})D\) given by (1.3) with ratios
we observe that \(\varLambda _0=\varLambda _2\) regardless of the value of the coefficient a. It happens that the simpler Olmsted–Goldbart model [12, 61, 75] for which \(( m_c: m_l: m_q) = (1:0:0)\) also yields \(\varLambda _0=\varLambda _2\). Thus in both these cases we have a tidier result.
Corollary 7.3
For the Beris–Edwards model and the Olmsted–Goldbart model the second order term \(f_2(\theta )\) of the bifurcation function has no zeros \(\theta \ne 0,\pi /2\in [0,\pi )\) if \({\tau _\lambda }/{\tau _\mu }\le 1\), while if \({\tau _\lambda }/{\tau _\mu }>1\) there are two zeros \(\theta =\pi /2\pm \varTheta \) with \(\varTheta \rightarrow 0\) as \({\tau _\lambda }/{\tau _\mu }\rightarrow 1\). \(\quad \square \)
These models both have \( m_c\ne 0\). If \( m_c=0\) with \( m_l\ne 0\) (so \(\varvec{L}({ Q})D\) has linear but no constant term) then \(\varLambda _0=0\) while \(\varLambda _2\ne 0\) and we see from (7.6) that \(f_2(\theta )\) does not vanish for any \(\theta \ne 0,\pi /2\bmod \pi \).
7.1 Periodic Orbits
Since
as in (6.52), the Implicit Function Theorem implies that if \(\theta =\theta _{\,0}\) is a simple zero of \(f_2\) then for sufficiently small \(|\beta |>0\) there exists a unique \(\theta _\beta \) close to \(\theta _{\,0}\) such that the right hand side of (7.8) vanishes at \(\theta =\theta _\beta \) and \(\theta _\beta \rightarrow \theta _{\,0}\) as \(\beta \rightarrow 0\). Thus \(\theta _\beta \) corresponds to a solution \(Z_\beta =Z(\theta _\beta ,\phi )\in {{\mathscr {M}}}_\phi \) to the bifurcation equation \({{\mathscr {F}}}(Z,\beta )=0\) for sufficiently small \(|\beta |>0\) with \(Z_\beta \rightarrow Z(\theta _{\,0},\phi )\) as \(\beta \rightarrow 0\).
In fact we know by Proposition 3.4 that the solutions \(\theta =0,\pi /2\) corresponding to the north pole \(Q^*\) and equator \({{\mathscr {C}}}\) do persist for sufficiently small \(|\beta |>0\), and we verify that
and so the north pole solution is always a simple solution, while the equator solution is a simple solution provided \(\varLambda _0\tau _\lambda \ne \varLambda _2\tau _\mu \). In general, if \(\theta =\theta _{\,0}:=\pi /2\pm \varTheta \) is another zero of \(f_2\), then
which is nonzero since \(\varLambda _0\tau _\lambda ,\varLambda _2\tau _\mu \) have the same sign by Corollary 7.2, and so \(\theta _{\,0}\) is also a simple solution.
When \(\varLambda _0=\varLambda _2\) as in the Beris–Edwards or Olmsted–Goldbart models we thus have the following result on periodic orbits after perturbation.
Corollary 7.4
For the Beris–Edwards or Olmsted–Goldbart models under Assumptions 1–4 for fixed \(\lambda ,\mu \) with \(\tau _\lambda /\tau _\mu <1\) the equator \({{\mathscr {C}}}\) is the unique periodic orbit on \({\mathscr {O}}\) (other than the equilibrium \({ Q}^*\)) that persists for sufficiently small \(|\beta |>0\); its period is close to \(\pi /\omega \). For \(\tau _\lambda /\tau _\mu >1\) there is, in addition, \(\beta _0>0\) and a smooth path \(\{Q(\beta ):|\beta |<\beta _0\}\) in V with \({ Q}(0)=Z(\theta ,\phi )\in {{\mathscr {M}}}_\phi \) where \(\theta =\pi /2\pm \varTheta \) as in Corollary 7.3 such that there is a periodic orbit of (1.2) through \({ Q}(\beta )\) with period \(T({ Q}(\beta ),\beta )\rightarrow T_0=2\pi /\omega \) as \(\beta \rightarrow 0\). \(\quad \square \)
The perturbed equator represents a periodic orbit close to tumbling, possibly with a small kayaking and/or biaxial component. The periodic orbit through \({ Q}(\beta )\) represents a kayaking orbit that (for fixed \(\lambda ,\mu \)) arises from a particular kayaking orbit on \({\mathscr {O}}\) persisting after perturbation. The two values \(\theta =\pi /2\pm \varTheta \) correspond to the two intersections of the same periodic orbit with the Poincaré section: see the geometric description at the end of Section 2.3. Thus if (sufficiently small) \(\beta \ne 0\) is fixed and \(\tau _\lambda /\tau _\mu \) increases through 1, the equator tumbling orbit generates a kayaking orbit through a period-doubling bifurcation.
7.2 Stability
So far the discussion has rested on Assumption 3 ensuring the normal hyperbolicity of the \(\mathrm{SO}(3)\)-orbit \({\mathscr {O}}\) under the dynamics of the system (1.2) when \(\beta =0\). In this section we investigate dynamical stability of the periodic orbits on \({\mathscr {O}}\) that persist close to \({\mathscr {O}}\) for sufficiently small \(|\beta |>0\). A necessary condition for stability is that \({\mathscr {O}}\) itself be an attracting set, and so we make now the following further assumption:
Assumption 5
The eigenvalues \(\lambda , \mu \) of \({\mathrm D}G(Q^*)\) are negative.
Consequently the perturbed flow-invariant manifold \({\mathscr {O}}(\beta )\) is normally hyperbolic and attracting for sufficiently small \(|\beta |>0\), therefore the stability of any equilibrium or periodic orbit lying on \({\mathscr {O}}(\beta )\) is determined by its stability or otherwise relative to the system (1.2) restricted to \({\mathscr {O}}(\beta )\). The manifold \({\mathscr {O}}(\beta )\) can be seen as the image of a section of the normal bundle of \({\mathscr {O}}\), its intersection with \({{\mathscr {U}}}_{{\mathscr {M}}}^\varepsilon \) being the image \({{\mathscr {M}}}(\beta )\) of a section \(\tilde{\sigma }(\cdot ,\beta )\) of this normal bundle restricted to \({{\mathscr {M}}}={{\mathscr {M}}}_\phi \). The 1-manifold \({{\mathscr {M}}}(\beta )\) is invariant under the Poincaré map \(P(\cdot ,\beta )\), the restriction of \(P(\cdot ,\beta )\) to \({{\mathscr {M}}}(\beta )\) determining a 1-dimensional discrete dynamical system on \({{\mathscr {M}}}(\beta )\) whose fixed points correspond to periodic orbits (or fixed points) of \(F(\cdot ,\beta )\) on \({\mathscr {O}}(\beta )\).
In our analysis, rather than use \(\tilde{\sigma }(\cdot ,\beta )\) which is harder to compute, we have used \(\sigma (\cdot ,\beta )\) and the method of Lyapunov–Schmidt to construct a vector field
on \({{\mathscr {M}}}\) whose zeros correspond to the periodic orbits (or fixed points) of \(F(\cdot ,\beta )\) on \({\mathscr {O}}(\beta )\). It follows from the general Principle of Reduced Stability [45, 74] that stability of periodic orbits on \({\mathscr {O}}(\beta )\) corresponds to stability of the corresponding zeros of the vector field \({{\mathscr {F}}}(Z,\beta )E_{11}^Z\) on \({{\mathscr {M}}}\) in the present context where \(\dim ({{\mathscr {M}}})=1\). However, we now show this directly, using a simple geometric argument taken from [16, Section 9.4]. Recall that in terms of the \(\theta \)-coordinate for Z on \({{\mathscr {M}}}\) we have \({{\mathscr {F}}}(Z,\beta )=f(\theta ,\beta )\).
Proposition 7.5
For fixed \(\beta \), let \({ Q}_0(\beta ):=Z_0+\tilde{\sigma }(Z_0,\beta )\in {{\mathscr {M}}}(\beta )\) be a hyperbolic fixed point for the Poincaré map \(P(\cdot , \beta )\), with \(Z_0=Z(\theta _{\,0},\phi )\) for \(\theta _{\,0}\) a hyperbolic zero of the system \({\dot{\theta }}=f(\theta ,\beta )\) on \({{\mathscr {M}}}\). Then \({ Q}_0(\beta )\) is stable (attracting) if and only if \(\theta _{\,0}\) is stable (attracting).
Proof
Suppose this fails for a given fixed value of \(\beta \), so that (without loss of generality) \({ Q}(\beta )\) is attracting on \({{\mathscr {M}}}(\beta )\) while \(\theta _{\,0}\) is repelling on \({{\mathscr {M}}}\). In particular this means that there is an interval \((\theta _-,\theta _{\,0})\) such that all corresponding points on \({{\mathscr {M}}}(\beta )\) are moved to the right (greater \(\theta \)-value) by the Poincaré map \(P(\cdot ,\beta )\), and there is also an interval \((\theta _{\,0},\theta _+)\) on which \(f(\theta ,\beta )>0\). Now consider a perturbation of the system (1.2) which adds a vector field of the form \({ Q}\mapsto \zeta ({ Q})E_{11}^Z\) where \(\zeta :V\rightarrow {{\mathbb {R}}}\) is a smooth non-negative bump function with \(\zeta ({ Q}(\beta ))>0\) and vanishing outside a sufficiently small neighbourhood U of \({ Q}(\beta )\) in V. Note that such a perturbation will be far from \(\mathrm{SO}(3)\)-equivariant as it is localised on U. For sufficiently small \(\zeta \) the effect of the perturbation will be to ensure that there is a larger open interval \(J_-\supset (\theta _-,\theta _{\,0}]\) on which corresponding points on \({{\mathscr {M}}}(\beta )\) are moved to the right, while there is a larger open interval \(J_+\supset [\theta _{\,0},\theta _+)\) on which \(f(\theta ,\beta )>0\). Therefore the fixed point \({ Q}(\beta )\) of the perturbed Poincaré map must have \(\theta \)-coordinate greater than \(\theta _{\,0}\), while the zero of \(f(\cdot ,\beta )\) is a point on \({{\mathscr {M}}}\) with \(\theta \)-coordinate less than \(\theta _{\,0}\). However, this contradicts the fact that fixed points of the Poincaré map correspond to zeros of the bifurcation function via projection in the normal bundle over \({{\mathscr {M}}}\), and so proves the Proposition. \(\square \)
Corollary 7.6
Under Assumptions 1–5, if \(\theta \) is a simple zero of \(f(\cdot ,\beta )\) then the corresponding periodic orbit (or fixed point) of (1.2) is linearly stable or unstable according as \({\mathrm d}f_2(\theta ,0)/{\mathrm d}\theta \) is negative or positive. \(\quad \square \)
7.3 Stable Kayaking Orbits
We are now able to describe the global dynamics close to \({\mathscr {O}}\) for the Beris–Edwards model, under the standing Assumptions 1–5. From Corollary 7.4 and (7.9), (7.10) we deduce the following stability result:
Theorem 7.7
For the Beris–Edwards model first suppose \(\varLambda _2>0\). Then for \(\tau _\lambda /\tau _\mu <1\) and sufficiently small \(|\beta |>0\) the perturbed equator \({{\mathscr {C}}}(\beta )\) is an attracting limit cycle (close to tumbling) on the invariant manifold \({\mathscr {O}}(\beta )\) that is the perturbed \(\mathrm{SO}(3)\)-orbit \({\mathscr {O}}\), its basin of attraction on \({\mathscr {O}}(\beta )\) being the whole of \({\mathscr {O}}(\beta )\) apart from the perturbed equilibrium \({ Q}^*\!(\beta )\) (log-rolling). For \(\tau _\lambda /\tau _\mu >1\) the perturbed equator \({{\mathscr {C}}}(\beta )\) is a repelling limit cycle, and there is precisely one other limit cycle on \({\mathscr {O}}(\beta )\): this limit cycle (kayaking) is attracting, and has period approximately twice that of \({{\mathscr {C}}}(\beta )\). If \(\varLambda _2<0\) the attraction/repulsion is reversed. \(\square \)
For the simpler Olmsted–Goldbart model we have \(\varLambda _2= m_c^2>0\) and so stability of the kayaking orbit (when it exists) automatically holds. In general, we have
and so the stability condition \(\varLambda _2>0\) holds precisely when \(w<-4a\) or \(w>2a\) where \(w:= m_c/ m_l\), supposing \( m_l\ne 0\). If \( m_l=0\),\(\, m_c\ne 0\) the kayaking orbit is automatically stable if it exists, while if \( m_l\ne 0\), \(\, m_c=0\) there is no kayaking orbit. For the Beris–Edwards model we have \(w=2/3\), and in this case stability depends on the coefficient a and holds automatically given that \(a<1/3\). Thus, to summarise, we have
Corollary 7.8
For the Beris–Edwards and Olmsted–Goldbart models, if the \(\mathrm{SO}(3)\)-orbit of the logrolling equilibrium \({ Q}^*\) is normally hyperbolic and attracting (so that \({ Q}^*\) is a stable equilibrium state in the absence of the shear flow, up to rigid rotations) then the kayaking orbit, when it exists, is an asymptotically stable limit cycle.
Remark 7.9
Given Assumption 5 the condition \(\tau _\lambda /\tau _\mu >1\) is the same as \(\tau _\lambda <\tau _\mu \), that is,
where
Our result on kayaking orbits for the Beris–Edwards model can therefore be expressed as follows:
Theorem 7.10
For the Beris–Edwards model (1.2), (1.3) the condition for the existence of a kayaking orbit for sufficiently small \(|\beta |>0\) is that \(\lambda -\mu \) and \(4\omega ^2-\lambda \mu \) have opposite signs; such a kayaking orbit is automatically linearly stable given that \(a<1/3\) for physical reasons (see (2.2)). \(\quad \square \)
7.4 The Gradient Case
In the Beris–Edwards model and others widely used in the literature the equivariant interaction field G is the negative gradient of a smooth free energy function \(V\rightarrow {{\mathbb {R}}}\) which is frame-indifferent, thus invariant under the action of \(\mathrm{SO}(3)\) on V. From general theory [71], such a function has the form
where \(f:{{\mathbb {R}}}^m\rightarrow {{\mathbb {R}}}\) is a smooth function and \(\{X_1,X_2,\ldots ,X_m\}\) are a basis for the ring of \(\mathrm{SO}(3)\)-invariant polynomials on V. It is well known in the liquid crystal literature (see for example [52, eq.(4.9)]) that such a basis is given by \(\{X,Y\}\), where
a proof being given in [33, Ch.XV, §6] via reduction to the group of symmetries of an equilateral triangle. Note that for \({ Q}\in V\) the Cayley–Hamilton Theorem shows immediately that \(\mathrm{tr}\,{ Q}^3=3\det { Q}\).
With \(f_X,f_Y\) denoting the partial derivatives of f we find that the functions \(g ,{\bar{g}} \) of (A.9) are then given by
and so, for their derivatives,
The equilibrium condition (A.10) is
where \(f_X^*,f_Y^*\) denote \(f_X({ Q}^*),f_Y(Q^*)\) respectively. The eigenvalues of \({\mathrm D}G({ Q}^*)\) are \(\lambda ,\mu \) and 0 where by (A.14) and (A.15),
with \(\varDelta f_X^*:={\mathrm D}f_X({ Q}^*){ Q}^*\) and likewise \(\varDelta f_Y^*\). For the particular and important case of the Landau - de Gennes potential
in which \(b,c>0\), we have
and
giving
The equilibrium condition (7.14) is thus that the coefficient \(a>0\) should satisfy
and the eigenvalues \(\lambda ,\mu \) are given by
Here \(\mu \) is automatically negative, and it is straightforward to check that (7.22) has two real solutions \(0< a_1 < a_2\) provided \(0<\tau <b^2/(24c)\). Then \(a_2>\frac{1}{2}(a_1+a_2)=b/(12c)\), and so \(\lambda <0\) for \(a=a_2\) and we choose \(a=a_2\) in the definition of \({ Q}^*\).
Corollary 7.11
In this setting the result of Theorem 7.10 giving the condition for the existence of kayaking orbits becomes
with stability for \(a=a_2<1/3\). \(\quad \square \)
It is natural to ask for what range of values of \(b,c,\tau \) and \(\omega \) these conditions can simultaneously hold.
Proposition 7.12
A necessary condition for the existence of stable kayaking orbits is \(b<4c\). Given that this holds, if \(5b<2c\) such orbits exist for all \(\omega >0\) while if \(5b>2c\), they exist for
The range of \(\tau \) or which these orbits exist is given by
Proof
From (7.23) the condition \(\lambda <0\) is \(a>b/(12c)\) given that \(a>0\), so the condition \(a<1/3\) for stability (and physicality) implies \(b<4c\). Then
and this corresponds to (7.25) since \(\tau (a):= ab-6a^2c\) is monotonic decreasing on \(J_0\) (its maximum is at \(a=b/(12c)\)) and we have \(\tau (1/3)=(b-2c)/3\) while \(\tau (b/(12c))=b^2/(24c)\). With the notation
the kayaking condition (7.24) is
since \(\var** (a)+\varOmega (a)=3b\) may be written as
This holds if and only if \(\varOmega (a)\) lies in the open interval \(J_1\) bounded by 3b and \(4\omega ^2/(3b)\), so the condition for the existence of a stable kayaking orbit (for some choice of \(\tau \)) is, therefore,
Now \(\varOmega (b/(12c))=0\) and \(\varOmega (1/3)=(4c-b)/3>0\), and so
hence (7.30) holds if and only if
Observe that
and so, if \(5b<2c\), then (7.31) automatically holds (regardless of \(\omega \)), while if \(5b>2c\), the condition (7.31) is
as stated. \(\quad \square \)
8 Conclusion
The geometry of uniaxial and biaxial nematic liquid crystal phases is most naturally expressed in terms of the action of the rotation group \(\mathrm{SO}(3)\) on the 5-dimensional space V of (symmetric, traceless) \({ Q}\)-tensors. In this paper we have used techniques from bifurcation theory related to symmetry, applied to a rather general class of ODEs on V widely used to model a homogeneous nematic liquid crystal in a simple shear flow, in order to prove the existence under certain conditions of an asymptotically stable limit cycle representing a ‘kayaking’ orbit, where the principal axis of molecular orientation of the ensemble of rigid rods lies out of the shear plane and rotates periodically about the vorticity axis. Our key assumption, however, is that the dynamical effect of the symmetric part of the flow-gradient tensor should be small compared to that of the anti-symmetric (rotational) part, so that the system we study is viewed as a perturbation of the co-rotational case which involves only the (frame-indifferent) molecular interaction field in addition to the rotation of the fluid. The results require expansion to second order in the perturbation parameter, as a consequence of the assumed linearity of the molecular aligning effect of the flow in terms of its velocity gradient. In cases where the molecular interaction field is the negative gradient of a free energy function, such as the Landau-de Gennes fourth order potential, we give explicit criteria on the coefficients to ensure the existence of the stable kayaking orbit for sufficiently small contribution from the symmetric part of the flow gradient. The admissible size of this contribution is not estimated, so that care must be taken in interpreting experimental or numerical verification.
Notes
Throughout the paper we take smooth to mean \(C^\infty \) although the results hold with sufficient finite order of differentiability.
References
Abud, M., Sartori, G.: The geometry of spontaneous symmetry breaking. Ann. Phys. 150(2), 307–372, 1983
Ambrosetti, A., Prodi, G.: A Primer of Nonlinear Analysis. Cambridge University Press, Cambridge 1993
Ball, J.M., Majumdar, A.: Nematic liquid crystals: from Maier-Saupe to a continuum theory. Mol. Cryst. Liq. Cryst. 525(1), 1–11, 2010. https://doi.org/10.1080/15421401003795555
Beris, A.N., Edwards, B.J.: Thermodynamics of Flowing Systems with Internal Microstructure. Oxford University Press, Oxford 1994
Buică, A., Françoise, J.-P., Llibre, J.: Periodic solutions of nonlinear periodic differential systems with a small parameter. Commun. Pure Appl. Anal. 6, 103–111, 2007
Burghardt, W.R., Fuller, G.G.: Transient shear flow of nematic liquid crystals: manifestations of director tumbling. J. Rheol. 34, 959–992, 1990. https://doi.org/10.1122/1.550151
Candido, M.R., Llibre, J., Novaes, D.D.: Persistence of periodic solutions for higher order perturbed differential systems via Lyapunov-Schmidt reduction. Nonlinearity 30, 3560–3586, 2017
Cavaterra, C., Rocca, E., Wu, H., Xu, X.: Global strong solutions of the full Navier-Stokes and \(Q\)-tensor system for nematic liquid crystal flows in two dimensions. SIAM J. Math. Anal. 48, 1368–1399, 2016. https://doi.org/10.1137/15M1048550
Chen, Y., Leung, A.Y.T.: Bifurcation and Chaos in Engineering. Springer, London 1998
Chicone, C.: Lyapunov-Schmidt reduction and Melnikov integrals for bifurcation of periodic solutions in coupled oscillators. J. Diff. Equ. 112, 407–447, 1994
Chicone, C.: A geometric approach to regular perturbation theory with an application to hydrodynamics. Trans. Am. Math. Soc. 347(12), 4559–4598, 1995
Chillingworth, D.R.J.; Vicente Alonso, E.; Wheeler, A.A.: Geometry and dynamics of a nematic liquid crystal in a uniform shear flow. J. Phys. A Math. Gen. 34, 1393–1404, 2001
Choate, E., Forest, M.G.: Dependence of the dynamic moduli of heterogeneous nematic polymers on planar anchoring relative to flow direction. Rheol Acta 50(9–10), 767–778, 2011
Chossat, P.: The Reduction of equivariant dynamics to the orbit space for compact group actions. Acta Appl Math 70, 71–94, 2002
Chossat, P., Lauterbach, R.: Methods in Equivariant Bifurcations and Dynamical Systems. World Scientific, Singapore 2000
Chow, S.-N., Hale, J.K.: Methods of Bifurcation Theory. Springer, New York 1982
de Gennes, P.G., Prost, J.: The Physics of Liquid Crystals, 2nd edn. Clarendon Press, Oxford 1993
Denniston, C., Marenduzzo, D., Orlandini, E., Yeomans, J.M.: Lattice Boltzmann algorithm for three-dimensional liquid-crystal hydrodynamics. Philos. Trans. R. Soc. A. 362, 1745–1754, 2014
Doi, M.: Molecular dynamics and rheological properties of concentrated solutions of rodlike polymers in isotropic and liquid crystalline phases. J. Polym. Sci. 19, 229–243, 1981
Du, H., Hu, X., Wang, C.: Suitable weak solutions for the co-rotational Beris-Edwards system in dimension three. Arch. Ration. Mech. Anal. 238, 749–803, 2020. https://doi.org/10.1007/s00205-020-01554-y
Faraoni, V., Grosso, M., Crescitelli, S., Maffettone, P.L.: The rigid-rod model for nematic polymers: an analysis of the shear flow problem. J. Rheol. 43, 829–843, 1999
Farhoudi, Y.; Rey, A.D.: Shear flows of nematic polymers. I. Orienting modes, bifurcations, and steady state rheological predictions. J. Rheol. 37, 289–314, 1993
Feng, J.; Chaubal, C.V.; Leal, L.G.: Closure approximations for the Doi theory: Which to use in simulating complex flows of liquid-crystalline polymers? J. Rheol. 42, 1095–1119, 1998
Fenichel, N.: Persistence and smoothness of invariant manifolds for flows. Indiana Univ. Math. J. 21, 193–226, 1971
Field, M.J.: Dynamics and Symmetry. Imperial College Press, London 2007
Forest, M.G., Zhou, R., Wang, Q.: Symmetries of the Doi kinetic theory for nematic polymers of arbitrary aspect ratio: at rest and in linear flows. Phys. Rev. E 66, 2002
Forest, M.G., Wang, Q.: Monodomain response of finite-aspect-ratio macromolecules in shear and related linear flows. Rheol. Acta 42, 20–46, 2003
Forest, M.G., Zhou, R., Wang, Q.: Full-tensor alignment criteria for sheared nematic polymers. J. Rheol. 47, 105–127, 2003
Forest, M.G., Wang, Q., Zhou, R.: The weak shear kinetic phase diagram for nematic polymers. Rheol. Acta 43, 17–37, 2004
Forest, M.G., Wang, Q., Zhou, R.: The flow-phase diagram of Doi-Hess theory for sheared nematic polymers II: finite shear rates. Rheol. Acta 44, 80–93, 2004
Fox, R.J., Forest, M.G., Pickens, S.J., Dingemans, T.J.: Observation of transition cascades in sheared liquid crystalline polymers. Soft Matter 16, 3891–3901, 2020
Golubitsky, M., Schaeffer, D.G.: Singularities and Groups in Bifurcation Theory, vol. I. Springer, New York 1985
Golubitsky, M., Schaeffer, D.G., Stewart, I.: Singularities and Groups in Bifurcation Theory, vol. II. Springer, New York 1988
Griffiths, P.A., Harris, J.E.: Principles of Algebraic Geometry. Wiley, New York 1978
Grosso, M., Keunings, R., Crescitelli, S., Maffettone, P.L.: Prediction of chaotic dynamics in sheared liquid crystalline polymers. Phys. Rev. Lett. 86, 3184–3187, 2001
Hand, G.L.: A theory of anisotropic fluids. J. Fluid Mech. 13, 33–46, 1962
Hale, J.K.: Ordinary Differential Equations. Interscience Publishers, New York 1969
Hale, J. K.: Introduction to dynamic bifurcation. In: Salvadori, L. (ed.) Bifurcation Theory and Applications. Lect. Notes Math., vol. 1057, pp. 106–151. Springer, Berlin (1984)
Harris, J.A.: Algebraic Geometry: A First Course. Springer, New York 1992
He, L., LeBris, C., Lelievre, T.: Periodic long-time behavior for an approximate model of nematic polymers. Kinet. Relat. Models 5, 357–382, 2012
Hess, S.: Fokker-Planck equation approach to flow alignment in liquid crystals. Z. Naturforsch. 31, 1034–1037, 1976
Hirsch, M.W., Pugh, C.C., Shub, M.: Invariant Manifolds. Lect. Notes Math., vol. 583. Springer, Berlin (1977)
Hoyle, R.: Pattern Formation. Cambridge University Press, Cambridge 2006
Kielhöfer, H.: Bifurcation Theory. Springer, New York 2004
Kielhöfer, H., Lauterbach, R.: On the principle of reduced stability. J. Funct. Anal. 53, 99–111, 1983
Kröger, M., Ammar, A., Chinesta, F.: Consistent closure schemes for statistical models of anisotropic fluids. J. Non-Newton. Fluid Mech. 149(1–3), 40–55, 2008
Larson, R.G., Öttinger, H.C.: Effect of molecular elasticity on out-of-plane orientations in shearing flow of liquid-crystalline polymers. Macromolecules 24, 6270–6282, 1991
Lee, J.; Forest, M.G.; Zhou, R.: Alignment and rheo-oscillator criteria for sheared nematic polymer films in the monolayer limit. Discrete Contin. Dyn. Syst. (DCDS) Ser. B 6, 339–356, 2006
Lefschetz, S.: Differential Equations: Geometric Theory, 2nd edn. Interscience Publishers, New York 1957
Llibre, J., Novaes, D.D., Teixeira, M.A.: Higher order averaging theory for finding periodic solutions via Brouwer degree. Nonlinearity 27, 563–583, 2014
MacMillan, E.H.: Slow flows of anisotropic fluids. J. Rheol. 33, 1071–1105, 1989
MacMillan, E.H.: On the hydrodynamics of biaxial nematic liquid crystals. Part 1: general theory. Arch. Ration. Mech. Anal. 117, 193–239, 1992
MacMillan, E.H.: On the hydrodynamics of biaxial nematic liquid crystals.Part 2: steady-state analysis. Arch. Ration. Mech. Anal. 117, 241–294, 1992
Maffettone, P.L., Sonnet, A.M., Virga, E.G.: Shear-induced biaxiality in nematic polymers. J. Non-Newton. Fluid Mech. 90, 283–297, 2000
Maffettone, P.L., Crescitelli, S.: Bifurcation analysis of a molecular model for nematic polymers in shear flows. J. Non-Newton. Fluid Mech. 59, 73–91, 1995
Marrucci, G., Maffettone, P.L.: Description of the liquid crystalline phase of rodlike polymers at high shear rates. Macromolecules 22, 4076–4082, 1989
Marsden, J.E.: Qualitative methods in bifurcation theory. Bull. Am. Math. Soc. 84(6), 1125–1148, 1978
Michel, L., Zhilinskii, B.I.: Symmetry, invariants, topology. Basic tools. Phys. Rep. 341, 11–84, 2001
Mottram, N.J., Newton, C.J.P.: Introduction to Q-Tensor Theory. ar**v:1409.3542v2 (2014)
Murza, A.C.; Teruel, A.E.; Zarnescu, A.D.: Shear flow dynamics in the Beris-Edwards model of nematic liquid crystals. Proc. R. Soc. A 474, 2017.06783, 2018
Olmsted, P.D., Goldbart, P.M.: Isotropic-nematic transition in shear flow: state selection, coexistence, phase transitions, and critical behavior. Phys. Rev. A 46, 4966–4993, 1992
Olmsted, P.D., Lu, C.-Y.D.: Phase coexistence of complex fluids in a shear flow. Faraday Discuss. 112, 183–194, 1999
Paciu, M., Zarnescu, A.: Global existence and regularity for the full coupled Navier-Stokes and Q-tensor system. SIAM J. Math. Anal. 43, 2009–2049, 2011
Rienäcker, G., Hess, S.: Orientational dynamics of nematic liquid crystals under shear flow. Phys. A 267, 294–321, 1999
Rienäcker, G., Kröger, M., Hess, S.: Chaotic and regular shear-induced orientational dynamics of nematic liquid crystals. Phys. A 315, 537–568, 2002
Rienäcker, G., Kröger, M., Hess, S.: Chaotic orientational behavior of a nematic liquid crystal subjected to a steady shear flow. Phys. Rev. E 66, 040702(R), 2002
Rivlin, R.S., Ericksen, J.L.: Stress-deformation relations for isotropic materials. J. Ration. Mech. Anal. 4, 323–425, 1955
Rose, M.E.: Elementary Theory of Angular Momentum. Dover Publications, New York (1995). Reprint of 1957 original
Sattinger, D.H.: Bifurcation from rotationally invariant states. J. Math. Phys. 19, 1720–1732, 1978
Sattinger, D.H.: Group Theoretic Methods in Bifurcation Theory. Lect. Notes Math., vol. 762. Springer, Berlin (1979)
Schwartz, G.: Smooth functions invariant under the action of a compact Lie group. Topology 14, 63–68, 1975
Sonnet, A.M., Virga, E.G.: Dissipative Ordered Fluids: Theories for Liquid Crystals. Springer, New York 2010
Vanderbauwhede, A.: Local Bifurcation and Symmetry, Res. Notes in Math., vol. 75. Pitman, London (1982)
Vanderbauwhede, A.: Stability of bifurcating equilibria and the principle of reduced stability. In: Salvadori, L. (eds.) Bifurcation Theory and Applications. Lect. Notes Math., vol. 1057, pp. 209–223. Springer, Berlin (1984)
Vicente Alonso, E., Wheeler, A.A., Sluckin, T.J.: Nonlinear dynamics of a nematic liquid crystal in the presence of a shear flow. Proc. R. Soc. A 459, 195–220, 2003
Wu, H., Xu, X., Zarnescu, A.: Dynamics and flow effects in the Beris-Edwards system modeling nematic liquid crystals. Arch. Ration. Mech. Anal. 231, 1217–1267, 2019
Yang, X., Wang, Q., Mullins, W., Forest, M.G.: Dynamic defect morphology and hydrodynamics of sheared nematic polymers in two space dimensions. J. Rheol. 53(3), 589–615, 2009
Acknowledgements
This collaboration arose during a workshop at the Mathematics of Liquid Crystals Programme at the Isaac Newton Institute in Cambridge in 2013 where the problem of existence and stability of the kayaking orbit was raised by GF, remaining open in spite of decades of overwhelming numerical evidence together with convincing experimental evidence. An active discussion followed and co-authors DC, RL and CW continued to work, with intermittent exchanges with GF, toward the resolution presented here. The research was supported by the Isaac Newton Institute, Cambridge and (DC) a Leverhulme Emeritus Research Fellowship; in addition CW was grateful to the Free University Berlin for hospitality. The authors also express thanks to Jaume Llibre for helpful conversations about higher-order averaging, and to Stefano Turzi for valuable input concerning invariants.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by E. Virga
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The first three named authors dedicate this paper to the fond memory of our late colleague Claudia Wulff, who passed away between the first provisional acceptance of this paper and its eventual publication. Throughout our work her cheerfulness, enthusiasm, clear geometric insight and scrupulous attention to detail have continually inspired us and sustained this project. We are grateful to have had the good fortune to share this collaboration over many years with her.
C. Wulff: Deceased 12 June 2021
Appendices
Equivariant Maps and Vector Fields
A map (vector field) \(G:V\rightarrow V\) is equivariant (sometimes called covariant) with respect to a subgroup \(\Sigma \) of \(\mathrm{SO}(3)\) (or \(\Sigma \)-equivariant) when it respects all the symmetries represented by \(\Sigma \), that is,
for all \(R\in \Sigma \) and all \({ Q}\in V\). Differentiating (A.1) with respect to \({ Q}\) gives
Thus \({\mathrm D}G({\widetilde{R}}{ Q})\) is conjugate to \({\mathrm D}G({ Q})\) so they have the same eigenvalues, while \({\widetilde{R}}\) takes the eigenvectors of \({\mathrm D}G({ Q})\) to those of \({\mathrm D}G({\widetilde{R}}{ Q})\). In particular if \({ Q}\) is fixed by the subgroup \(\Sigma \) of \(\mathrm{SO}(3)\) then (A.2) reads as
for \(R\in \Sigma \), so the linear map \({\mathrm D}G({ Q}):V \rightarrow V\) is also \(\Sigma \)-equivariant.
Differentiating (A.2) with respect to \({ Q}\) gives the expression
for \(H,K\in V\) and \(R\in \mathrm{SO}(3)\). Therefore in the case when \({ Q}\) is fixed by the subgroup \(\Sigma \) of \(\mathrm{SO}(3)\) the bilinear map \(B={\mathrm D}^2G({ Q})\) is \(\Sigma \)-equivariant in the sense that
for all \(H,K\in V\) and \(R\in \Sigma \).
Example A.1
Let \(G^{\,0}:V\rightarrow V\) be the \(\mathrm{SO}(3)\)-equivariant map \({ Q}\mapsto { Q}^2-\frac{1}{3}\mathrm{tr}({ Q}^2)I\). Here \({\mathrm D}G^{\,0}({ Q})H=[{ Q},H]^+\) for \(H\in V\), with the notation as in (1.4). Each \(Z\in {\mathscr {O}}\) is fixed by \(\Sigma _{{{\mathbf {z}}}}\) and so the linear map from V to V, given by \( H\mapsto [Z,H]^+\) is \(\Sigma _{{{\mathbf {z}}}}\)-equivariant. It therefore respects the isotypic decomposition (2.8) of V into \(\Sigma _{{{\mathbf {z}}}}\)-invariant eigenspaces of \( [Z,\cdot \,]^+\), with eigenvalues independent of \(Z\in {\mathscr {O}}\).
Using the characterisations of \(\{V_i^*\}\) given by (2.9)–(2.11) it is straightforward to calculate the corresponding eigenvalues for \(Z={ Q}^*\) and hence for all \(Z\in {\mathscr {O}}\).
Proposition A.2
For \(Z\in {\mathscr {O}}\) the eigenvalues for \( [Z,\cdot \,]^+\) corresponding to the eigenspaces \(V_0^Z,V_1^Z,V_2^Z\) are respectively
\(\quad \square \)
1.1 Bilinear Maps
From (2.14) and equivariance it follows that the element \(R_{{\mathbf {z}}}(\pi )\in \Sigma _{{\mathbf {z}}}\) acts on each isotypic component \(V_i^Z\) by
for \(v_i\in V_i^Z,\, i=0,1,2\), and so from (A.5) we see that any \(\Sigma _{{\mathbf {z}}}\)-equivariant bilinear map \(B:V\times V\rightarrow V=V_0^Z\oplus V_1^Z\oplus V_2^Z\) satisfies
Thus \({\widetilde{R}}_{{\mathbf {z}}}(\pi )\) fixes \(B(v_i,v_j)\) when \(i+j\) is even and multiplies it by \(-1\) when \(i+j\) is odd. As a consequence we have the following result, extremely useful for simplifying calculations:
Proposition A.3
For \(v_i\in V_i^Z, \,i=0,1,2\)
\(\square \)
Corollary A.4
If \({ Q}_i\) denotes the component of \({ Q}\) in \(V_i^Z,i=0,1,2\), then for \(H,K\in V\) the component \(B_1\) of B in \(V_1^Z\) is given by
\(\square \)
Corollary A.5
The result (A.8) applies to \(B={\mathrm D}^2G({ Q})\) for any \(\mathrm{SO}(3)\)-equivariant \(G:V\rightarrow V\) when \({ Q}\) is fixed by \(\Sigma _{{\mathbf {z}}}\). In particular it applies in the case of the quadratic map \(G^{\,0}:Q\mapsto { Q}^2-\frac{1}{3}\mathrm{tr}({ Q}^2)I\) of Example A.1 where we have \(B(H,K)={\mathrm D}^2G^{\,0}({ Q})(H,K)=[H,K]^+\) independent of \({ Q}\). \(\quad \square \)
1.2 Specific Form of G
It is a standard result from group representation theory that a basis for the module of smooth \(\mathrm{SO}(3)\)-equivariant vector fields over the ring of smooth \(\mathrm{SO}(3)\)-invariant functions on V is given by the pair of vector fields
(see [33, XV, Section 6 ] for example); in other words any smooth \(\mathrm{SO}(3)\)-equivariant map (or vector field) \(G:V\rightarrow V\) may be written in the form
where \(g ,{\bar{g}} :V\rightarrow {{\mathbb {R}}}\) are smooth \(\mathrm{SO}(3)\)-invariant functions. Thus G is completely determined once the two functions g and \({\bar{g}} \) are chosen.
The condition for \({ Q}=Q^*\) to be a zero of G is
using Proposition A.2, that is,
where \({\hat{g}}:=g + 2a{\bar{g}} \).
1.2.1 First Derivative of \(\mathbf {G}\)
Differentiating (A.9) we have for any \({ Q},H\in V\)
Therefore
where
With \(G({ Q}^*)=0\), this gives
using Proposition A.2 and (A.10), where \(g ^*\) denotes \(g ({ Q}^*)\) and \(\varDelta g ^*:={\mathrm D}g ({ Q}^*){ Q}^*\) etc..
Likewise, from (A.11), we find that
where
taking account of the fact that \({\mathrm D}g ({ Q}^*) E_2(\alpha ) ={\mathrm D}{\bar{g}} ({ Q}^*) E_2(\alpha ) =0\) by Proposition 2.2. Also,
using (A.10) and Proposition A.2, the result expected since \({\mathscr {T}}^*=\mathrm{span}\{E_1(\alpha )\}_{\alpha \in [0,\pi )}\). In summary we have
Proposition A.6
The eigenvalues of \({\mathrm D}G({ Q}^*)\) corresponding to the eigenspaces \(V_0^*,V_1^*,V_2^*\) are \(\lambda ,0,\mu \) respectively, with \(\lambda ,\mu \) given by (A.14) and (A.15). \(\quad \square \)
1.2.2 Second Derivative of G
Differentiating (A.11) again, we have, for \(H,K\in V\),
In the main text we need to evaluate the component of this expression tangent to the \(\mathrm{SO}(3)\)-orbit \({\mathscr {O}}\) of the uniaxial matrix \({ Q}^*\) at points \(Z\in {\mathscr {O}}\). Here we calculate this for \(Z={ Q}^*\) making significant use of Proposition A.3 and Corollary A.5, and will be able to transfer the result to a general \({ Q}=Z\in {\mathscr {O}}\) by applying the \(\mathrm{SO}(3)\) action.
Let \(G_1\) denote the component of G in \(V_1^*\), and write \(B_1=D^2G_1({ Q}^*)\).
Proposition A.7
-
1.
If \(H,K\in V_0^*\oplus V_2^*\) or \(H,K\in V_1^*\), then
$$\begin{aligned} B_1(H,K)= 0. \end{aligned}$$(A.17) -
2.
If \(H=H_0+H_2\in V_0^*\oplus V_2^*\) and \(K=K_1\in V_1^*\), then
$$\begin{aligned} B_1(H_0+H_2,K_1)&=\bigl ({\mathrm D}g ({ Q}^*)H_0\bigr )K_1 + 2\bigl ({\mathrm D}{\bar{g}} ({ Q}^*)H_0\bigr )[{ Q}^*,K_1]^+ \nonumber \\&\quad + 2{\bar{g}} ^*[H_0+H_2,K_1]^+ \nonumber \\&=\bigl ({\mathrm D}{\hat{g}}({ Q}^*)H_0\bigr )K_1+ 2{\bar{g}} ^*[H_0,K_1]^+ + 2{\bar{g}} ^*[H_2,K_1]^+. \end{aligned}$$(A.18)
Proof
The result (1) is immediate from Corollary A.4. Part (2) follows from (A.16), using the fact that \({ Q}^*\) and \([{ Q}^*,{ Q}^*]^+\) lie in \(V_0^*\), together with Proposition 2.2 applied to the \(\mathrm{SO}(3)\)-invariant functions g and \({\bar{g}}\). For the term involving \([{ Q}^*,K_1]^+\) we use the eigenvalue result from Proposition A.2. \(\quad \square \)
1.3 Explicit Expression for \( [H,K]^+_1\)
Finally, an explicit expression for the \(V_1^*\)-component \([H,K]^+_1\) of \([H,K]^+\) is needed in order to evaluate the bifurcation function (5.36). Using the identity
we see that
since \(E_1(-\pi /2)=-E_1(\pi /2)\) from (2.12). Then, writing
with respect to the basis \({{\mathscr {B}}}^*\) for V as given by (4.1), we find that
using (A.20) and (A.21). We therefore arrive at the following:
Proposition A.8
Proof
Let \(H = H_0 + H_1 + H_2\), \(K = K_0 + K_1 + K_2\) with \(H_i, K_i \in V_i^*\), \(i=0,1,2\). Using Corollary A.5 we see that
Since \(H_0=h_{01}E_0^Z = \tfrac{1}{\sqrt{6}a} h_{01} Z\) it follows from Proposition A.2 that \([H_0,K_1]^+=\tfrac{1}{\sqrt{6}} h_{01}K_1\). We then use (A.24) to obtain
Exchanging the roles of H and K gives the result. \(\quad \square \)
Corollary A.9
By \(\mathrm{SO}(3)\)-equivariance the same formula applies to give the \(V_1^Z\)-component of \([H,K]^+\), the coordinates (A.22), (A.23) in this case being taken with respect to the basis \({{\mathscr {B}}}^Z\). \(\quad \square \)
We can now be even more specific: the expression (A.18) simplifies to
using (A.14) and (A.15). Thus we conclude the following from Proposition A.7, (A.25) and (A.24):
Proposition A.10
For \(H = H_T + H_N\) and \( K = K_T + K_N\in V = V_1^*\oplus \bigl (V_0^*\oplus V_2^*\bigr )\) and \(B_1=D^2G_1({ Q}^*)\), we have
where, with notation as in (A.22), (A.23),
\(\square \)
Corollary A.11
By \(\mathrm{SO}(3)\)-equivariance the same expressions (A.27), (A.28) apply relative to the decomposition \(V = V_1^Z\oplus \bigl (V_0^Z\oplus V_2^Z\bigr )\). \(\quad \square \)
It is only \(\kappa _1\) that we need in the calculation of the bifurcation function.
General Form for \(\varvec{L}({ Q})D\)
The term \(\varvec{L}({ Q})D\) in (1.2) representing the effect on the dynamics of \({ Q}\) from the symmetric part D of the flow velocity gradient is \(\mathrm{SO}(3)\)-equivariant in \(({ Q},D)\) and linear in D. From the expression in [67, §40] giving the general form of an \(\mathrm{SO}(3)\)-equivariant (isotropic) polynomial matrix-valued function of two matrices (here \(3\times 3\)) we find that, in our context in V, we have
where the coefficients \(w_i=w_i({ Q},D), i=1,\ldots ,5\) are \(\mathrm{SO}(3)\)-invariant polynomials in \(({ Q},D)\) such that \(w_1,w_2,w_3\) are functions of \({ Q}\) only while \(w_4,w_5\) are linear in D. The only candidates for \(w_4\) or \(w_5\) are \(\mathrm{tr}({ Q}D)\) and \(\mathrm{tr}({ Q}^2 D)\) multiplied by invariant functions of \({ Q}\) alone, and thus we find, as in [52], that
where \(v_1,\ldots ,v_7\) are polynomial functions of \(\mathrm{tr}{ Q}^2\) and \(\mathrm{tr}{ Q}^3\) with \(v_i=w_i\) for \(i=1,2,3\) and
That (B.2) also holds in the smooth case follows from the results in [71].
Replacing D by \({\widetilde{D}}:={\widetilde{R}}_3(-\omega t)D\) in (B.2) and using the eigenspace properties of \([Z,\cdot \,]^+\) from Proposition A.2 to see that
we find that
where
evaluated at \({ Q}=Z\). Since the functions \(v_1,\ldots ,v_7\) are \(\mathrm{SO}(3)\)-invariant their values at Z are the same as their values at \({ Q}^*\) and depend only on a.
Observing from (4.30) that \(y(t,{ Q})\) is a linear function of D, as also is \(\chi (t,Z)\) from (6.27), we see that the expressions for y(t, Z) and \(\chi (t,Z)\) arising from (B.2) and (B.6) are therefore given by
with the notation of Section 6.3. Consequently the \(B_{11}^Z\) term in the second order term (5.36) of the bifurcation function is exactly as evaluated in Section 6.5 but with the coefficients \( m_c, m_l, m_q\) replaced by the coefficients \(v_1^*,v_2^*,v_4^*\), respectively.
Next, to obtain the \({\mathrm D}{\widetilde{\varvec{L}}}\) term of the second order term of the bifurcation function (5.36) we differentiate (B.1) with respect to \({ Q}\) at \({ Q}=Z\in {\mathscr {O}}\). For \(H\in V\), this gives
where \({\bar{w}}_i\) denotes the \({ Q}\)-derivative of \(w_i\) at \({ Q}=Z\) applied to H for \(i=1,\ldots ,5\). With p denoting \(p_{11}^Z\) and writing \(pH=H_{11}^Z\) etc. we see that the expression obtained by applying p to (B.9) simplifies to
where
from the eigenspace decomposition of Proposition A.2. Here we again use (B.5) as well as \([Z,{\widetilde{D}}\,]^+_{11}=a{\widetilde{D}}_{11}^Z\), and the coefficients \(w_i\) are evaluated at \({ Q}=Z\) so that, in particular from (B.3) and (B.4) with (B.5),
The contribution that (B.10) makes to the second order term \(F_2(Z)\) of the bifurcation function (5.36) is obtained by substituting \(\chi (t,Z)\) for H and integrating from \(t=0\) to \(t=T_0\). Since
we obtain
with
Hence, just as in Section 6.5, it is only \(\varvec{L}^l({ Q})\) (see (1.5)) that contributes to the \({\mathrm D}{\widetilde{\varvec{L}}}\) term in (5.36).
If \(w_3=0\) we therefore see that the second order term \(f_2(\theta )\) of the bifurcation function \(f(\theta )\) in the general case (B.2) is obtained from the expression (7.4) but now with the coefficients \( m_c, m_l, m_q\) that define \(\varLambda _0,\varLambda _2\) in (6.65) simply replaced by the coefficients \(v_1^*,v_2^*,v_4^*\) respectively. Observe that (B.2) corresponds to (1.5) with \(v_1,v_2,v_4= m_c, m_l, m_q\) and the remaining coefficients \(v_j=0\).
When \(w_3\ne 0\) there is the further term arising from \(\int _0^{T_0}p[{\hat{\chi }}(t,Z),{\widetilde{D}}\,]^+ {\mathrm d}t\). Writing (6.48) as
we see from (B.14) that
so that also from (6.33) we get
and from (6.61)
Consequently, in the second order term of the bifurcation function the coefficients \(\varLambda _0,\varLambda _2\) in (7.4) are replaced by their counterparts with the coefficients \(v_1^*,v_2^*,v_4^*\) in place of \( m_c, m_l, m_q\), together with the coefficients arising from (B.15), (B.16), (B.17), giving
where we recall that \(w_3=v_3\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chillingworth, D., Forest, M.G., Lauterbach, R. et al. Existence and Stability of Kayaking Orbits for Nematic Liquid Crystals in Simple Shear Flow. Arch Rational Mech Anal 242, 1229–1287 (2021). https://doi.org/10.1007/s00205-021-01703-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00205-021-01703-x