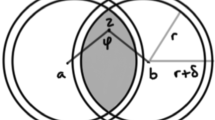
Abstract
The dodecahedral conjecture states that in a packing of unit spheres in \({\mathfrak{R}}^{3}\), the Voronoi cell of minimum possible volume is a regular dodecahedron with inradius one. The conjecture was first stated by L. Fejes Tóth in 1943, and was finally proved by Hales and McLaughlin over 50 years later using techniques developed by Hales for his proof of the Kepler conjecture. In 1964, Fejes Tóth described an approach that would lead to a complete proof of the dodecahedral conjecture if a key inequality were established. We describe a connection between the key inequality required to complete Fejes Tóth’s proof and bounds for spherical codes and show how recently developed strengthened bounds for spherical codes may make it possible to complete Fejes Tóth’s proof.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Fejes Tóth does not explicitly consider the possibility that the two faces \(F_{j}(\hat{x}_{1},\ldots,\hat{x}_{m})\) and \(F_{k}(\hat{x}_{1},\ldots,\hat{x}_{m})\) intersect. However in this case it is easy to see that the increase in volume that results from increasing \(\hat{x}_{j}\) is even less than if the faces do not intersect.
- 2.
Note that (1) implies that for m = 13, if \(\Vert \bar{x}_{i}\Vert = 1\) for i = 1, …, 12, then \(\Vert \bar{x}_{13}\Vert \geq R_{D}\). It has been incorrectly stated that the latter implication is the “missing ingredient” in Fejes Tóth’s proof. In fact the stronger statement (1) is exactly what is required.
- 3.
A rigorous lower bound for each \(v_{\mathrm{LP}}^{{\ast}}(m)\) can be obtained by solving the dual of the discretized problem and adjusting the dual solution to account for the discretization of s [3]. Alternatively a sum-of-squares formulation for the dual of LP(m) could be used to solve the dual problem exactly.
- 4.
A referee has indicated that geometric arguments due to Marchal should also be able to establish that (5) holds for these cases, and possibly m = 16.
- 5.
The values of \(v_{\mathrm{SDP}}^{{\ast}}(m)\) are approximate, based on solving a discretization of SDP(m). It is possible to obtain rigorous bounds by applying a sum-of-squares formulation to the dual of SDP(m); see [2].
- 6.
References
Anstreicher, K.M.: The thirteen spheres: a new proof. Discret. Comput. Geom. 31, 613–625 (2004)
Bachoc, C., Vallentin, F.: New upper bounds for kissing numbers from semidefinite programming. J. AMS 21, 909–924 (2008)
Conway, J.H., Sloane, N.J.A.: Sphere Packings, Lattices and Groups, 3rd edn. Springer, New York (1999)
Delsarte, P., Goethals, J.-M., Seidel, J.J.: Spherical codes and designs. Geom. Dedicata 6, 363–388 (1977)
Fejes Tóth, L.: Über die dichteste Kugellagerung. Math. Zeit. 48, 676–684 (1943)
Fejes Tóth, L.: Regular Figures. Pergamon Press, New York (1964)
Hales, T.C.: The strong dodecahedral conjecture and Fejes Tóth’s contact conjecture. Preprint, University of Pittsburgh. Available via ar**v. http://arxiv.org/abs/1110.0402v1 (2011)
Hales, T.C.: Dense Sphere Packings: A Blueprint for Formal Proofs. London Mathematical Society Lecture Note Series, vol. 400. Cambridge University Press, Cambridge/New York (2012)
Hales, T.C., McLaughlin, S.: A proof of the dodecahedral conjecture. J. AMS 23, 299–344 (2010)
Sloane, N.J.A.: Spherical codes (packings). http://www.research.att.com/~njas/packings
Acknowledgements
I would like to thank Tibor Csendes for providing an English translation of [5], and Frank Vallentin for independently verifying the computations based on SDP(m). I am also grateful to two anonymous referees for their careful readings of the paper and valuable suggestions to improve it.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Anstreicher, K.M. (2013). An Approach to the Dodecahedral Conjecture Based on Bounds for Spherical Codes. In: Bezdek, K., Deza, A., Ye, Y. (eds) Discrete Geometry and Optimization. Fields Institute Communications, vol 69. Springer, Heidelberg. https://doi.org/10.1007/978-3-319-00200-2_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-00200-2_3
Published:
Publisher Name: Springer, Heidelberg
Print ISBN: 978-3-319-00199-9
Online ISBN: 978-3-319-00200-2
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)