1 Introduction

Runtime verification complements traditional static verification techniques, by offering lightweight solutions for checking properties based on a single, possibly long execution trace of a given system [8]. We present new runtime verification techniques for the problem of bias detection in decision-making software. The use of software for making critical decisions about humans is a growing trend; example areas include judiciary [13, 20], policing [23, 49], banking [48], etc. It is important that these software systems are unbiased towards the protected attributes of humans, like gender, ethnicity, etc. However, they have often shown biases in their decisions in the past [20, 47, 55, 57, 58]. While there are many approaches for mitigating biases before deployment [20, 47, 55, 57, 58], recent runtime verification approaches [3, 34] offer a new complementary tool to oversee algorithmic fairness in AI and machine-learned decision makers during deployment.

To verify algorithmic fairness at runtime, the given decision-maker is treated as a generator of events with an unknown model. The goal is to algorithmically design lightweight but rigorous runtime monitors against quantitative formal specifications. The monitors observe a long stream of events and, after each observation, output a quantitative, statistically sound estimate of how fair or biased the generator was until that point in time. While the existing approaches [3, 34] considered only sequential decision making models and built monitors from the frequentist viewpoint in statistics, we allow the richer class of Markov chain models and present monitors from both the frequentist and the Bayesian statistical viewpoints.

Monitoring algorithmic fairness involves on-the-fly statistical estimations, a feature that has not been well-explored in the traditional runtime verification literature. As far as the algorithmic fairness literature is concerned, the existing works are mostly model-based, and either minimize decision biases of machine-learned systems at design-time (i.e., pre-processing) [11, 41, 65, 66], or verify their absence at inspection-time (i.e., post-processing) [32]. In contrast, we verify algorithmic fairness at runtime, and do not require an explicit model of the generator. On one hand, the model-independence makes the monitors trustworthy, and on the other hand, it complements the existing model-based static analyses and design techniques, which are often insufficient due to partially unknown or imprecise models of systems in real-world environments.

We assume that the sequences of events generated by the generator can be modeled as sequences of states visited by a finite unknown Markov chain. This implies that the generator is well-behaved and the events follow each other according to some fixed probability distributions. Not only is this assumption satisfied by many machine-learned systems (see Sect. 1.1 for examples), it also provides just enough structure to lay the bare-bones foundations for runtime verification of algorithmic fairness properties. We emphasize that we do not require knowledge of the transition probabilities of the underlying Markov chain.

We propose a new specification language, called the Probabilistic Specification Expressions (PSEs), which can formalize a majority of the existing algorithmic fairness properties in the literature, including demographic parity [21], equal opportunity [32], disparate impact [25], etc. Let Q be the set of events. Syntactically, a PSE is a restricted arithmetic expression over the (unknown) transition probabilities of a Markov chain with the state space Q. Semantically, a PSE \(\varphi \) over Q is a function that maps every Markov chain M with the state space Q to a real number, and the value \(\varphi (M)\) represents the degree of fairness or bias (with respect to \(\varphi \)) in the generator M. Our monitors observe a long sequence of events from Q, and after each observation, compute a statistically rigorous estimate of \(\varphi (M)\) with a PAC-style error bound for a given confidence level. As the observed sequence gets longer, the error bound gets tighter.

Algorithmic fairness properties that are expressible using PSEs are quantitative refinements of the traditional qualitative fairness properties studied in formal methods. For example, a qualitative fairness property may require that if a certain event A occurs infinitely often, then another event B should follow infinitely often. In particular, a coin is qualitatively fair if infinitely many coin tosses contain both infinitely many heads and infinitely many tails. In contrast, the coin will be algorithmically fair (i.e., unbiased) if approximately half of the tosses come up heads. Technically, while qualitative weak and strong fairness properties are \(\omega \)-regular, the algorithmic fairness properties are statistical and require counting. Moreover, for a qualitative fairness property, the satisfaction or violation cannot be established based on a finite prefix of the observed sequence. In contrast, for any given finite prefix of observations, the value of an algorithmic fairness property can be estimated using statistical techniques, assuming the future behaves statistically like the past (the Markov assumption).

As our main contribution, we present two different monitoring algorithms, using tools from frequentist and Bayesian statistics, respectively. The central idea of the frequentist monitor is that the probability of every transition of the monitored Markov chain M can be estimated using the fraction of times the transition is taken per visit to its source vertex. Building on this, we present a practical implementation of the frequentist monitor that can estimate the value of a given PSE from an observed finite sequence of states. For the coin example, after every new toss, the frequentist monitor will update its estimate of probability of seeing heads by computing the fraction of times the coin came up heads so far, and then by using concentration bounds to find a tight error bound for a given confidence level. On the other hand, the central idea of the Bayesian monitor is that we begin with a prior belief about the transition probabilities of M, and having seen a finite sequence of observations, we can obtain an updated posterior belief about M. For a given confidence level, the output of the monitor is computed by applying concentration inequalities to find a tight error bound around the mean of the posterior belief. For the coin example, the Bayesian monitor will begin with a prior belief about the degree of fairness, and, after observing the outcome of each new toss, will compute a new posterior belief. If the prior belief agrees with the true model with a high probability, then the Bayesian monitor’s output converges to the true value of the PSE more quickly than the frequentist monitor. In general, both monitors can efficiently estimate more complicated PSEs, such as the ratio and the squared difference of the probabilities of heads of two different coins. The choice of the monitor for a particular application depends on whether an objective or a subjective evaluation, with respect to a given prior, is desired.

Both frequentist and Bayesian monitors use registers (and counters as a restricted class of registers) to keep counts of the relevant events and store the intermediate results. If the size of the given PSE is n, then, in theory, the frequentist monitor uses \(\mathcal {O}(n^42^n)\) registers and computes its output in \(\mathcal {O}(n^42^n)\) time after each new observation, whereas the Bayesian monitor uses \(\mathcal {O}(n^22^n)\) registers and computes its output in \(\mathcal {O}(n^22^n)\) time after each new observation. The computation time and the required number of registers get drastically reduced to \( O (n^2)\) for the frequentist monitor with PSEs that contain up to one division operator, and for the Bayesian monitor with polynomial PSEs (possibly having negative exponents in the monomials). This shows that under given circumstances, one or the other type of the monitor can be favorable computation-wise. These special, efficient cases cover many algorithmic fairness properties of interest, such as demographic parity and equal opportunity.

Our experiments confirm that our monitors are fast in practice. Using a prototype implementation in Rust, we monitored a couple of decision-making systems adapted from the literature. In particular, we monitor if a bank is fair in lending money to applicants from different demographic groups [48], and if a college is fair in admitting students without creating an unreasonable financial burden on the society [54]. In our experiments, both monitors took, on an average, less than a millisecond to update their verdicts after each observation, and only used tens of internal registers to operate, thereby demonstrating their practical usability at runtime.

In short, we advocate that runtime verification introduces a new set of tools in the area of algorithmic fairness, using which we can monitor biases of deployed AI and machine-learned systems in real-time. While existing monitoring approaches only support sequential decision making problems and use only the frequentist statistical viewpoint, we present monitors for the more general class of Markov chain system models using both frequentist and Bayesian statistical viewpoints.

All proofs can be found in the longer version of the paper [33].

1.1 Motivating Examples

We first present two real-world examples from the algorithmic fairness literature to motivate the problem; these examples will later be used to illustrate the technical developments.

The Lending Problem [48]: Suppose a bank lends money to individuals based on certain attributes, like credit score, age group, etc. The bank wants to maximize profit by lending money to only those who will repay the loan in time—called the “true individuals.” There is a sensitive attribute (e.g., ethnicity) classifying the population into two groups g and \(\overline{g}\). The bank will be considered fair (in lending money) if its lending policy is independent of an individual’s membership in g or \(\overline{g}\). Several group fairness metrics from the literature are relevant in this context. Disparate impact [25] quantifies the ratio of the probability of an individual from g getting the loan to the probability of an individual from \(\overline{g}\) getting the loan, which should be close to 1 for the bank to be considered fair. Demographic parity [21] quantifies the difference between the probability of an individual from g getting the loan and the probability of an individual from \(\overline{g}\) getting the loan, which should be close to 0 for the bank to be considered fair. Equal opportunity [32] quantifies the difference between the probability of a true individual from g getting the loan and the probability of a true individual from \(\overline{g}\) getting the loan, which should be close to 0 for the bank to be considered fair. A discussion on the relative merit of various different algorithmic fairness notions is out of scope of this paper, but can be found in the literature [15, 22, 43, 62]. We show how we can monitor whether a given group fairness criteria is fulfilled by the bank, by observing a sequence of lending decisions.

The College Admission Problem [54]: Consider a college that announces a cutoff of grades for admitting students through an entrance examination. Based on the merit, every truly qualified student belongs to group g, and the rest to group \(\overline{g}\). Knowing the cutoff, every student can choose to invest a sum of money—proportional to the gap between the cutoff and their true merit—to be able to reach the cutoff, e.g., by taking private tuition classes. On the other hand, the college’s utility is in minimizing admission of students from \(\overline{g}\), which can be accomplished by raising the cutoff to a level that is too expensive to be achieved by the students from \(\overline{g}\) and yet easy to be achieved by the students from g. The social burden associated to the college’s cutoff choice is the expected expense of every student from g, which should be close to 0 for the college to be considered fair (towards the society). We show how we can monitor the social burden, by observing a sequence of investment decisions made by the students from g.

1.2 Related Work

There has been a plethora of work on algorithmic fairness from the machine learning standpoint [10, 12, 21, 32, 38, 42, 45, 46, 52, 59, 63, 66]. In general, these works improve algorithmic fairness through de-biasing the training dataset (pre-processing), or through incentivizing the learning algorithm to make fair decisions (in-processing), or through eliminating biases from the output of the machine-learned model (post-processing). All of these are interventions in the design of the system, whereas our monitors treat the system as already deployed.

Recently, formal methods-inspired techniques have been used to guarantee algorithmic fairness through the verification of a learned model [2, 9, 29, 53, 61], and enforcement of robustness [6, 30, 39]. All of these works verify or enforce algorithmic fairness statically on all runs of the system with high probability. This requires certain knowledge about the system model, which may not be always available. Our runtime monitor dynamically verifies whether the current run of an opaque system is fair.

Our frequentist monitor is closely related to the novel work of Albarghouthi et al. [3], where the authors build a programming framework that allows runtime monitoring of algorithmic fairness properties on programs. Their monitor evaluates the algorithmic fairness of repeated “single-shot” decisions made by machine-learned functions on a sequence of samples drawn from an underlying unknown but fixed distribution, which is a special case of our more general Markov chain model of the generator. They do not consider the Bayesian point of view. Moreover, we argue and empirically show in Sect. 4 that our frequentist approach produces significantly tighter statistical estimates than their approach on most PSEs. On the flip side, their specification language is more expressive, in that they allow atomic variables for expected values of events, which is useful for specifying individual fairness criteria [21]. We only consider group fairness, and leave individual fairness as part of future research. Also, they allow logical operators (like boolean connectives) in their specification language. However, we obtain tighter statistical estimates for the core arithmetic part of algorithmic fairness properties (through PSEs), and point out that we can deal with logical operators just like they do in a straightforward manner.

Shortly after the first manuscript of this paper was written, we published a separate work for monitoring long-run fairness in sequential decision making problems, where the feature distribution of the population may dynamically change due to the actions of the individuals [34]. Although this other work generalizes our current paper in some aspects (support for dynamic changes in the model), it only allows sequential decision making models (instead of Markov chains) and does not consider the Bayesian monitoring perspective.

There is a large body of research on monitoring, though the considered properties are mainly temporal [5, 7, 19, 24, 40, 50, 60]. Unfortunately, these techniques do not directly extend to monitoring algorithmic fairness, since checking algorithmic fairness requires statistical methods, which is beyond the limit of finite automata-based monitors used by the classical techniques. Although there are works on quantitative monitoring that use richer types of monitors (with counters/registers like us) [28, 35, 36, 56], the considered specifications do not easily extend to statistical properties like algorithmic fairness. One exception is the work by Ferrère et al. [26], which monitors certain statistical properties, like mode and median of a given sequence of events. Firstly, they do not consider algorithmic fairness properties. Secondly, their monitors’ outputs are correct only as the length of the observed sequence approaches infinity (asymptotic guarantee), whereas our monitors’ outputs are always correct with high confidence (finite-sample guarantee), and the precision gets better for longer sequences.

Although our work uses similar tools as used in statistical verification [1, 4, 14, 17, 64], the goals are different. In traditional statistical verification, the system’s runs are chosen probabilistically, and it is verified if any run of the system satisfies a boolean property with a certain probability. For us, the run is given as input to the monitor, and it is this run that is verified against a quantitative algorithmic fairness property with statistical error bounds. To the best of our knowledge, existing works on statistical verification do not consider algorithmic fairness properties.

2 Preliminaries

For any alphabet \(\varSigma \), the notation \(\varSigma ^*\) represents the set of all finite words over \(\varSigma \). We write \(\mathbb {R}\), \(\mathbb {N}\), and \(\mathbb {N}^+\) to denote the sets of real numbers, natural numbers (including zero), and positive integers, respectively. For a pair of real (natural) numbers a, b with \(a < b\), we write [a, b] (\([a. .b]\)) to denote the set of all real (natural) numbers between and including a and b. For a given \(c,r\in \mathbb {R}\), we write \([c \pm r]\) to denote the set \([c-r,c+r]\). For simpler notation, we will use \(|\cdot |\) to denote both the cardinality of a set and the absolute value of a real number, whenever the intended use is clear.

For a given vector \(v\in \mathbb {R}^n\) and a given \(m\times n\) real matrix M, for some m, n, we write \(v_i\) to denote the i-th element of v and write \(M_{ij}\) to denote the element at the i-th row and the j-th column of M. For a given \(n\in \mathbb {N}^+\), a simplex is the set of vectors \(\varDelta (n){:}{=}\lbrace x\in [0,1]^{n+1} \mid \sum _{i=1}^{n+1} x_i = 1\rbrace \). Notice that the dimension of \(\varDelta (n)\) is \(n+1\) (and not n), a convention that is standard due to the interpretation of \(\varDelta (n)\) as the \(n+1\) vertices of an n-dimensional polytope. A stochastic matrix of dimension \(m\times m\) is a matrix whose every row is in \(\varDelta (m-1)\), i.e. \(M\in \varDelta (m-1)^m\). Random variables will be denoted using uppercase symbols from the Latin alphabet (e.g. X), while the associated outcomes will be denoted using lowercase font of the same symbol (x is an outcome of X). We will interchangeably use the expected value \(\mathbb {E}(X)\) and the mean \(\mu _X\) of X. For a given set S, define \(\mathcal {D}(S)\) as the set of every random variable—called a probability distributionFootnote 1—with set of outcomes being \(2^S\). A Bernoulli random variable that produces “1” (the alternative is “0”) with probability p is written as \( Bernoulli (p)\).

2.1 Markov Chains as Randomized Generators of Events

We use finite Markov chains as sequential randomized generators of events. A (finite) Markov chain \(\mathcal {M}\) is a triple \( (Q,M,\pi )\), where \(Q=[1. .N]\) is a set of states for a finite N, \(M\in \varDelta (N-1)^N\) is a stochastic matrix called the transition probability matrix, and \(\pi \in \mathcal {D}(Q)\) is the distribution over initial states. We often refer to a pair of states \((i,j)\in Q\times Q\) as an edge. The Markov chain \(\mathcal {M}\) generates an infinite sequence of random variables \(X_0=\pi ,X_1,\ldots \), with \(X_i\in \mathcal {D}(Q)\) for every i, such that the Markov property is satisfied: \(\mathbb {P}(X_{n+1} = i_{n+1} \mid X_0=i_0,\ldots ,X_n=i_n) = \mathbb {P}(X_{n+1}=i_{n+1} \mid X_n=i_n)\), which is \(M_{i_ni_{n+1}}\) in our case. A finite path \(\vec {x}=x_0,\ldots ,x_n\) of \(\mathcal {M}\) is a finite word over \(Q\) such that for every \(t\in [0;n]\), \(\mathbb {P}(X_t=x_t)>0\). Let \( Paths (\mathcal {M})\) be the set of every finite path of \(\mathcal {M}\).

We use Markov chains to model the probabilistic interaction between a machine-learned decision maker with its environment. Intuitively, the Markov assumption on the model puts the restriction that the decision maker does not change over time, e.g., due to retraining.

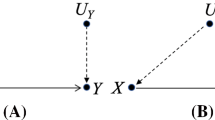
In Fig. 1 we show the Markov chains for the lending and the college admission examples from Sect. 1.1. The Markov chain for the lending example captures the sequence of loan-related probabilistic events, namely, that a loan applicant is randomly sampled and the group information (g or \(\overline{g}\)) is revealed, a probabilistic decision is made by the decision-maker and either the loan was granted (gy or \(\overline{g}y\), depending on the group) or refused (\(\overline{y}\)), and if the loan is granted then with some probabilities it either gets repaid (z) or defaulted (\(\overline{z}\)). The Markov chain for the college admission example captures the sequence of admission events, namely, that a candidate is randomly sampled and the group is revealed (\(g,\overline{g}\)), and when the candidate is from group g (truly qualified) then the amount of money invested for admission is also revealed.

Fig. 1.
figure 1

Markov chains for the lending and the college-admission examples. (left) The lending example: The state \(\textit{init}\) denotes the initiation of the sampling, and the rest represent the selected individual, namely, g and \(\overline{g}\) denote the two groups, (gy) and \((\overline{g}y)\) denote that the individual is respectively from group g and group \(\overline{g}\) and the loan was granted, \(\overline{y}\) denotes that the loan was refused, and z and \(\overline{z}\) denote whether the loan was repaid or not. (right) The college admission example: The state init denotes the initiation of the sampling, the states \(g,\overline{g}\) represent the group identity of the selected candidate, and the states \(\lbrace 0,\ldots ,N\rbrace \) represent the amount of money invested by a truly eligible candidate.

Full size image

2.2 Randomized Register Monitors

Randomized register monitors, or simply monitors, are adapted from the (deterministic) polynomial monitors of Ferrère et al. [27]. Let R be a finite set of integer variables called registers. A function \(v:R\rightarrow \mathbb {N}\) assigning concrete value to every register in R is called a valuation of R. Let \(\mathbb {N}^R\) denote the set of all valuations of R. Registers can be read and written according to relations in the signature \(S=\langle 0,1,+,-,\times ,\div ,\le \rangle \). We consider two basic operations on registers:

  • A test is a conjunction of atomic formulas over S and their negation;

  • An update is a map** from variables to terms over S.

We use \(\varPhi (R)\) and \(\varGamma (R)\) to respectively denote the set of tests and updates over R. Counters are special registers with a restricted signature \(S=\langle 0,1,+,-,\le \rangle \).

Definition 1 (Randomized register monitor)

A randomized register monitor is a tuple \(\left( \varSigma ,\varLambda ,R,\lambda ,T \right) \) where \(\varSigma \) is a finite input alphabet, \(\varLambda \) is an output alphabet, R is a finite set of registers, \(\lambda :\mathbb {N}^R\rightarrow \varLambda \) is an output function, and \(T:\varSigma \times \varPhi (R)\rightarrow \mathcal {D}(\varGamma (R))\) is the randomized transition function such that for every \(\sigma \in \varSigma \) and for every valuation \(v\in \mathbb {N}^R\), there exists a unique \(\phi \in \varPhi (R)\) with \(v\models \phi \) and \(T(\sigma ,\phi )\in \mathcal {D}(\varGamma (R))\). A deterministic register monitor is a randomized register monitor for which \(T(\sigma ,\phi )\) is a Dirac delta distribution, if it is defined.

A state of a monitor \(\mathcal {A}\) is a valuation of its registers \(v\in \mathbb {N}^R\). The monitor \(\mathcal {A}\) transitions from state v to a distribution over states given by the random variable \(Y=T(\sigma ,\phi )\) on input \(\sigma \in \varSigma \) if there exists \(\phi \) such that \(v\models \phi \). Let \(\gamma \) be an outcome of Y with \(\mathbb {P}(Y=\gamma )>0\), in which case the registers are updated as \(v'(x)=v(\gamma (x))\) for every \(x\in R\), and the respective concrete transition is written as \(v\xrightarrow {\sigma } v'\). A run of \(\mathcal {A}\) on a word \(w_0\ldots w_n\in \varSigma ^*\) is a sequence of concrete transitions \(v_0\xrightarrow {w_0} v_1\xrightarrow {w_1}\ldots \xrightarrow {w_n} v_{n+1}\). The probabilistic transitions of \(\mathcal {A}\) induce a probability distribution over the sample space of finite runs of the monitor, denoted \(\widehat{\mathbb {P}}(\cdot )\). For a given finite word \(w\in \varSigma ^*\), the semantics of the monitor \(\mathcal {A}\) is given by a random variable \([\![\mathcal {A}]\!](w){:}{=}\lambda (Y)\) inducing the probability measure \(\mathbb {P}_\mathcal {A}\), where Y is the random variable representing the distribution over the final state in a run of \(\mathcal {A}\) on the word w, i.e., \(\mathbb {P}_\mathcal {A}(Y=v) {:}{=}\widehat{\mathbb {P}}(\lbrace r=r_0\ldots r_m\in \varSigma ^*\mid r \text { is a run of } \mathcal {A}\text { on } w \text { and } r_m=v\rbrace )\).

Example: A Monitor for Detecting the (Unknown) Bias of a Coin. We present a simple deterministic monitor that computes a PAC estimate of the bias of an unknown coin from a sequence of toss outcomes, where the outcomes are denoted as “h” for heads and “t” for tails. The input alphabet is the set of toss outcomes, i.e., \(\varSigma =\lbrace h,t\rbrace \), the output alphabet is the set of every bias intervals, i.e., \(\varGamma = \lbrace [a,b]\mid 0\le a<b\le 1\rbrace \), the set of registers is \(R=\lbrace r_n,r_h\rbrace \), where \(r_n\) and \(r_h\) are counters counting the total number of tosses and the number of heads, respectively, and the output function \(\lambda \) maps every valuation of \(r_n,r_h\) to an interval estimate of the bias that has the form , where \(\delta \in [0,1]\) is a given upper bound on the probability of an incorrect estimate and \(\varepsilon (r_n,\delta )\) is the estimation error computed using PAC analysis. For instance, after observing a sequence of 67 tosses with 36 heads, the values of the registers will be \(v(r_n)=67\) and \(v(r_h)=36\), and the output of the monitor will be for some appropriate \(\varepsilon (\cdot )\). Now, suppose the next input to the monitor is h, in which case the monitor’s transition is given as \(T(h,\cdot ) = (r_n+1,r_h+1)\), which updates the registers to the new values \(v'(r_n)=67+1=68\) and \(v'(r_h)=36+1=37\). For this example, the tests \(\varPhi (R)\) over the registers are redundant, but they can be used to construct monitors for more complex properties.

3 Algorithmic Fairness Specifications and Problem Formulation

3.1 Probabilistic Specification Expressions

To formalize algorithmic fairness properties, like the ones in Sect. 1.1, we introduce probabilistic specification expressions (PSE). A PSE \(\varphi \) over a given finite set \(Q\) is an algebraic expression with some restricted set of operations that uses variables labeled \(v_{ij}\) with \(i,j\in Q\) and whose domains are the real interval [0, 1]. The syntax of \(\varphi \) is:

$$\begin{aligned} \xi&::= v\in \lbrace v_{ij}\rbrace _{i,j\in Q} \ | \ \xi \cdot \xi \ | \ 1\div \xi , \end{aligned}$$
(1a)
$$\begin{aligned} \varphi&::= \kappa \in \mathbb {R} \ | \ \xi \ | \ \varphi + \varphi \ | \ \varphi - \varphi \ | \ \varphi \cdot \varphi \ | \ (\varphi ), \end{aligned}$$
(1b)

where \(\lbrace v_{ij}\rbrace _{i,j\in Q}\) are the variables with domain [0, 1] and \(\kappa \) is a constant. The expression \(\xi \) in (1a) is called a monomial and is simply a product of powers of variables with integer exponents. A polynomial is a weighted sum of monomials with constant weights.Footnote 2 Syntactically, polynomials form a strict subclass of the expressions definable using (1b), because the product of two polynomials is not a polynomial, but is a valid expression according to (1b). A PSE \(\varphi \) is division-free if there is no division operator involved in \(\varphi \). The size of an expression \(\varphi \) is the total number of arithmatic operators (i.e. \(+,-,\cdot ,\div \)) in \(\varphi \). We use \(V_\varphi \) to denote the set of variables appearing in the expression \(\varphi \), and for every \(V\subseteq V_\varphi \) we define \( Dom (V){:}{=}\lbrace i\in Q\mid \exists v_{ij}\in V \vee \exists v_{ki}\in V\rbrace \) as the set containing any state of the Markov chain that is involved in some variable in V.

The semantics of a PSE \(\varphi \) is interpreted statically on the unknown Markov chain M: we write \(\varphi (M)\) to denote the evaluation or the value of \(\varphi \) by substituting every variable \(v_{ij}\) in \(\varphi \) with \(M_{ij}\). E.g., for a Markov chain with state space \(\lbrace 1,2\rbrace \) and transition probabilities \(M_{11}=0.2\), \(M_{12}=0.8\), \(M_{21}=0.4\), and \(M_{22}=0.6\), the expression \(\varphi = v_{11}-v_{21}\) has the evaluation \(\varphi (M) = 0.2-0.4 = -0.2\). We will assume that for every expression \((1\div \xi )\), \(\xi (M)\ne 0\).

Example: Group Fairness. Using PSEs, we can express the group fairness properties for the lending example described in Sect. 1.1, with the help of the Markov chain in the left subfigure of Fig. 1:

         Disparate impact [25]:                     \(v_{gy}\div v_{\overline{g}y}\)

         Demographic parity [21]:                \(v_{gy}-v_{\overline{g}y}\)

The equal opportunity criterion requires the following probability to be close to zero: \( p = \mathbb {P}(y\mid g,z)-\mathbb {P}(y\mid \overline{g},z), \) which is tricky to monitor as p contains the counter-factual probabilities representing “the probability that an individual from a group would repay had the loan been granted.” We apply Bayes’ rule, and turn p into the following equivalent form: \( p'=\frac{\mathbb {P}(z\mid g,y)\cdot \mathbb {P}(y\mid g)}{\mathbb {P}(z\mid g)} - \frac{\mathbb {P}(z\mid \overline{g},y)\cdot \mathbb {P}(y\mid \overline{g})}{\mathbb {P}(z\mid \overline{g})}. \) Assuming \(\mathbb {P}(z\mid g)=c_1\) and \(\mathbb {P}(z\mid \overline{g})=c_2\), where \(c_1\) and \(c_2\) are known constants, the property \(p'\) can be encoded as a PSE as below:

      Equal opportunity [32]:                  \((v_{(gy)z}\cdot v_{gy})\div c_1 - ( v_{(\overline{g}y)z}\cdot v_{\overline{g}y}) \div c_2\).

Example: Social Burden. Using PSEs, we can express the social burden of the college admission example described in Sect. 1.1, with the help of the Markov chain depicted in the right subfigure of Fig. 1:

         Social burden [54]:                        \(1\cdot v_{g1} + \ldots + N\cdot v_{gN}\).

3.2 The Monitoring Problem

Informally, our goal is to build monitors that observe a single long path of a Markov chain and, after each observation, output a new estimate for the value of the PSE. Since the monitor’s estimate is based on statistics collected from a finite path, the output may be incorrect with some probability, where the source of this probability is different between the frequentist and the Bayesian approaches. In the frequentist approach, the underlying Markov chain is fixed (but unknown), and the randomness stems from the sampling of the observed path. In the Bayesian approach, the observed path is fixed, and the randomness stems from the uncertainty about a prior specifying the Markov chain’s parameters. The commonality is that, in both cases, we want our monitors to estimate the value of the PSE up to an error with a fixed probabilistic confidence.

We formalize the monitoring problem separately for the two approaches. A problem instance is a triple \(\left( Q,\varphi ,\delta \right) \), where \(Q=[1. .N]\) is a set of states, \(\varphi \) is a PSE over \(Q\), and \(\delta \in [0,1]\) is a constant. In the frequentist approach, we use \(\mathbb {P}_s\) to denote the probability measure induced by sampling of paths, and in the Bayesian approach we use \(\mathbb {P}_\theta \) to denote the probability measure induced by the prior probability density function \(p_\theta :\varDelta (n-1)^n\rightarrow \mathbb {R}\cup \{\infty \}\) over the transition matrix of the Markov chain. In both cases, the output alphabets of the monitors contain every real interval.

Problem 1

(Frequentist monitor). Suppose \(\left( Q,\varphi ,\delta \right) \) is a problem instance given as input. Design a monitor \(\mathcal {A}\) such that for every Markov chain \(\mathcal {M}\) with transition probability matrix \(M\) and for every finite path \(\vec {x}\in Paths (\mathcal {M})\):

$$\begin{aligned} \mathbb {P}_{s,\mathcal {A}}\left( \varphi (M)\in [\![\mathcal {A}]\!](\vec {x})\right) \ge 1-\delta , \end{aligned}$$
(2)

where \(\mathbb {P}_{s,\mathcal {A}}\) is the joint probability measure of \(\mathbb {P}_s\) and \(\mathbb {P}_\mathcal {A}\).

Problem 2

(Bayesian monitor). Suppose \(\left( Q,\varphi ,\delta \right) \) is a problem instance and \(p_\theta \) is a prior density function, both given as inputs. Design a monitor \(\mathcal {A}\) such that for every Markov chain \(\mathcal {M}\) with transition probability matrix \(M\) and for every finite path \(\vec {x}\in Paths (\mathcal {M})\):

$$\begin{aligned} \mathbb {P}_{\theta ,\mathcal {A}}\left( \varphi (M)\in [\![\mathcal {A}]\!](\vec {x})\mid \vec {x}\right) \ge 1-\delta , \end{aligned}$$
(3)

where \(\mathbb {P}_{\theta ,\mathcal {A}}\) is the joint probability measure of \(\mathbb {P}_\theta \) and \(\mathbb {P}_\mathcal {A}\).

Notice that the state space of the Markov chain and the input alphabet of the monitor are the same, and so, many times, we refer to observed states as (input) symbols, and vice versa. The estimate \([l,u]=[\![\mathcal {A}]\!](\vec {x})\) is called the \((1-\delta )\cdot 100\%\) confidence interval for \(\varphi (M)\).Footnote 3 The radius, given by \(\varepsilon =0.5\cdot (u-l)\), is called the estimation error, and the quantity \(1-\delta \) is called the confidence. The estimate gets more precise as the error gets smaller and the confidence gets higher.

In many situations, we are interested in a qualitative question of the form “is \(\varphi (M)\le c\)?” for some constant c. We point out that, once the quantitative problem is solved, the qualitative questions can be answered using standard procedures by setting up a hypothesis test [44, p. 380].

4 Frequentist Monitoring

Suppose the given PSE is only a single variable \(\varphi =v_{ij}\), i.e., we are monitoring the probability of going from state i to another state j. The frequentist monitor \(\mathcal {A}\) for \(\varphi \) can be constructed in two steps: (1) empirically compute the average number of times the edge (i, j) was taken per visit to the state i on the observed path of the Markov chain, and (2) compute the \((1-\delta )\cdot 100\%\) confidence interval using statistical concentration inequalities.

Fig. 2.
figure 2

Variation of ratio of the est. error using the existing approach [3] to est. error using our approach, w.r.t. the size of the chosen PSE.

Full size image

Now consider a slightly more complex PSE \(\varphi '=v_{ij}+v_{ik}\). One approach to monitor \(\varphi '\), proposed by Albarghouthi et al. [3], would be to first compute the \((1-\delta )\cdot 100\%\) confidence intervals \([l_1,u_1]\) and \([l_2,u_2]\) separately for the two constituent variables \(v_{ij}\) and \(v_{ik}\), respectively. Then, the \((1-2\delta )\cdot 100\%\) confidence interval for \(\varphi '\) would be given by the sum of the two intervals \([l_1,u_1]\) and \([l_2,u_2]\), i.e., \([l_1+l_2,u_1+u_2]\); notice the drop in overall confidence due to the union bound. The drop in the confidence level and the additional error introduced by the interval arithmetic accumulate quickly for larger PSEs, making the estimate unusable. Furthermore, we lose all the advantages of having any dependence between the terms in the PSE. For instance, by observing that \(v_{ij}\) and \(v_{ik}\) correspond to the mutually exclusive transitions i to j and i to k, we know that \(\varphi '(M)\) is always less than 1, a feature that will be lost if we use plain merging of individual confidence intervals for \(v_{ij}\) and \(v_{ik}\). We overcome these issues by estimating the value of the PSE as a whole as much as possible. In Fig. 2, we demonstrate how the ratio between the estimation errors from the two approaches vary as the number of summands (i.e., n) in the PSE \(\varphi =\sum _{i=1}^n v_{1n}\) changes; in both cases we fixed the overall \(\delta \) to 0.05 (\(95\%\) confidence). The ratio remains the same for different observation lengths. Our approach is always at least as accurate as their approach [3], and is significantly better for larger PSEs.

4.1 The Main Principle

We first explain the idea for division-free PSEs, i.e., PSEs that do not involve any division operator; later we extend our approach to the general case.

Divison-Free PSEs: In our algorithm, for every variable \(v_{ij}\in V_\varphi \), we introduce a \( Bernoulli ({M_{ij}})\) random variable \(Y^{ij}\) with the mean \({M_{ij}}\) unknown to us. We make an observation \(y^{ij}_p\) for every p-th visit to the state i on a run, and if j follows immediately afterwards then record \(y^{ij}_p=1\) else record \(y^{ij}_p=0\). This gives us a sequence of observations \(\vec {y}^{ij}=y^{ij}_1,y^{ij}_2,\ldots \) corresponding to the sequence of i.i.d. random variables \(\vec {Y}^{ij}= Y^{ij}_1,Y^{ij}_2,\ldots \). For instance, for the run 121123 we obtain \(\vec {y}^{12}=1,0,1\) for the variable \(v_{12}\).

The heart of our algorithm is an aggregation procedure of every sequence of random variable \(\lbrace \vec {Y}^{ij}\rbrace _{v_{ij}\in V_{\varphi }}\) to a single i.i.d. sequence \(\vec {W}\) of an auxiliary random variable W, such that the mean of W is \(\mu _W =\mathbb {E}(W) = \varphi (M)\). We can then use known concentration inequalities on the sequence \(\vec {W}\) to estimate \(\mu _W\). Since \(\mu _{W}\) exactly equals \(\varphi (M)\) by design, we obtain a tight concentration bound on \(\varphi (M)\). We informally explain the main idea of constructing \(\vec {W}\) using simple examples; the details can be found in Algorithm 2.

Sum and Difference: Let \(\varphi = v_{ij} + v_{kl}\). We simply combine \(\vec {Y}^{ij}\) and \(\vec {Y}^{kl}\) as \(W_p = Y^{ij}_p + Y^{kl}_p\), so that \(w_p = y^{ij}_p+y^{kl}_p\) is the corresponding observation of \(W_p\). Then \(\mu _{W_p} = \varphi (M)\) holds, because \(\mu _{W_p} = \mathbb {E}(W_p) = \mathbb {E}(Y^{ij}_p + Y^{kl}_p) = \mathbb {E}(Y^{ij}_p) + \mathbb {E}(Y^{kl}_p) = M_{ij} + M_{kl}\). Similar approach works for \(\varphi = v_{ij} - v_{kl}\).

Multiplication: For multiplications, the same linearity principle will not always work, since for random variables A and B, \(\mathbb {E}(A\cdot B)=\mathbb {E}(A)\cdot \mathbb {E}(B)\) only if A and B are statistically independent, which will not be true for specifications of the form \(\varphi = v_{ij}\cdot v_{ik}\). In this case, the respective Bernoulli random variables \(Y^{ij}_p\) and \(Y^{ik}_p\) are dependent: \(\mathbb {P}(Y^{ij}_p=1)\cdot \mathbb {P}(Y^{ik}_p=1)=M_{ij}\cdot M_{ik}\), but \(\mathbb {P}(Y^{ij}_p=1 \wedge Y^{ik}_p=1)\) is always 0 (since both j and k cannot be visited following the p-th visit to i).

To benefit from independence once again, we temporally shift one of the random variables by defining \(W_p = Y^{ij}_{2p}\cdot Y^{ik}_{2p+1}\), with \(w_p = y^{ij}_{2p}\cdot y^{ik}_{2p+1}\). Since the random variables \(Y^{ij}_{2p}\) and \(Y^{ik}_{2p+1}\) are independent, as they use separate visits of state i, hence we obtain \(\mu _{W_p} = M_{ij}\cdot M_{ik}\). For independent multiplications of the form \(\varphi = v_{ij}\cdot v_{kl}\) with \(i\ne k\), we can simply use \(W_p = Y^{ij}_{p}\cdot Y^{ik}_{p}\).

In general, we use the ideas of aggregation and temporal shift on the syntax tree of the PSE \(\varphi \), inductively. With an aggregated sequence of observations for the auxiliary variable W for \(\varphi \), we can find an estimate for \(\varphi (M)\) using the Hoeffding’s inequality. We present the detailed algorithm of this monitor, namely FreqMonitorDivFree, in Algorithm 1.

The General Case (PSEs With Division Operators): We observe that every arbitrary PSE \(\varphi \) of size n can be transformed into a semantically equivalent PSE of the form \(\varphi _a+\frac{\varphi _b}{\varphi _c}\) of size \(\mathcal {O}(n^22^n)\), where \(\varphi _a\), \(\varphi _b\), and \(\varphi _c\) are all division-free. Once in this form, we can employ three different FreqMonitorDivFree monitors from Algorithm 1 to obtain separate interval estimates for \(\varphi _a\), \(\varphi _b\), and \(\varphi _c\), which are then combined using standard interval arithmetic and the resulting confidence of the estimate is obtained through the union bound. The steps for constructing the (general-case) FrequentistMonitor are shown in Algorithm 2, and the detailed analysis can be found in the proof of Theorem 1.

Bounding Memory: Consider a PSE \(\varphi =v_{ij}+v_{kl}\). The outcome \(w_p\) for \(\varphi \) can only be computed when both the Bernoulli outcomes \(y^{ij}_p\) and \(y^{kl}_p\) are available. If at any point only one of the two is available, then we need to store the available one so that it can be used later when the other one gets available. It can be shown that the storage of “unmatched” outcomes may need unbounded memory.

To bound the memory, we use the insight that a random reshuffling of the i.i.d. sequence \(y^{ij}_p\) would still be i.i.d. with the same distribution, so that we do not need to store the exact order in which the outcomes appeared. Instead, for every \(v_{ij}\in V_\varphi \), we only store the number of times we have seen the state i and the edge (i, j) in counters \(c_i\) and \(c_{ij}\), respectively. Observe that \(c_i\ge \sum _{v_{ik}\in V_\varphi } c_{ik}\), where the possible difference accounts for the visits to irrelevant states, denoted as a dummy state \(\top \). Given \(\lbrace c_{ik}\rbrace _{k}\), whenever needed, we generate in \(x_i\) a random reshuffling of the sequence of states, together with \(\top \), seen after the past visits to i. From the sequence stored in \(x_i\), for every \(v_{ik}\in V_\varphi \), we can consistently determine the value of \(y^{ik}_p\) (consistency dictates \(y^{ik}_p=1\Rightarrow y^{ij}_p=0\)). Moreover, we reuse space by resetting \(x_i\) whenever the sequence stored in \(x_i\) is no longer needed. It can be shown that the size of every \(x_i\) can be at most the size of the expression [33, Proof of Thm. 2]. This random reshuffling of the observation sequences is the cause of the probabilistic transitions of the frequenitst monitor.

4.2 Implementation of the Frequentist Monitor

Fix a problem instance \(\left( Q,\varphi ,\delta \right) \), with size of \(\varphi \) being n. Let \(\varphi \) be transformed into \(\varphi ^l\) by relabeling duplicate occurrences of \(v_{ij}\) using distinct labels \(v_{ij}^1,v_{ij}^2,\ldots \). The set of labeled variables in \(\varphi ^l\) is \(V_\varphi ^l\), and \(|V_\varphi ^l|=\mathcal {O}(n)\). Let \( SubExpr (\varphi )\) denote the set of every subexpression in the expression \(\varphi \), and use \([l_\varphi , u_\varphi ]\) to denote the range of values the expression \(\varphi \) can take for every valuation of every variable as per the domain [0, 1]. Let \( Dep (\varphi )=\lbrace i\mid \exists v_{ij}\in V_{\varphi }\rbrace \), and every subexpression \(\varphi _1\cdot \varphi _2\) with \( Dep (\varphi _1)\cap Dep (\varphi _2)\ne \emptyset \) is called a dependent multiplication.

Implementation of \(\texttt {FreqMonitorDivFree} \) in Algorithm 1 has two main functions. \( Init \) initializes the registers. \( Next \) implements the transition function of the monitor, which attempts to compute a new observation w for \(\vec {W}\) (Line 4) after observing a new input \(\sigma '\), and if successful it updates the output of the monitor by invoking the \( UpdateEst \) function. In addition to the registers in \( Init \) and \( Next \) labeled in the pseudocode, following registers are used internally:

  • \(x_i,\, i\in Dom (V_{\varphi })\): reshuffled sequence of states that followed i.

  • \(t^{l}_{ij}\): the index of \(x_i\) that was used to obtain the latest outcome of \(v_{ij}^l\).

figure c
figure d

Now, we summarize the main results for the frequentist monitor.

Theorem 1 (Correctness)

Let \((Q,\varphi ,\delta )\) be a problem instance. Algorithm 2 implements a monitor for \((Q,\varphi ,\delta )\) that solves Problem 1.

Theorem 2 (Computational resources)

Let \((Q,\varphi ,\delta )\) be a problem instance and \(\mathcal {A}\) be the monitor implemented using the FrequentistMonitor routine of Algorithm 2. Suppose the size of \(\varphi \) is n. The monitor \(\mathcal {A}\) requires \(\mathcal {O}(n^42^{2n})\) registers, and takes \(\mathcal {O}(n^42^{2n})\) time to update its output after receiving a new input symbol. For the special case of \(\varphi \) containing at most one division operator (division by constant does not count), \(\mathcal {A}\) requires only \(\mathcal {O}(n^2)\) registers, and takes only \(\mathcal {O}(n^2)\) time to update its output after receiving a new input symbol.

There is a tradeoff between the estimation error, the confidence, and the length of the observed sequence of input symbols. For instance, for a fixed confidence, the longer the observed sequence is, the smaller is the estimation error. The following theorem establishes a lower bound on the length of the sequence for a given upper bound on the estimation error and a fixed confidence.

Theorem 3 (Convergence speed)

Let \((Q,\varphi ,\delta )\) be a problem instance where \(\varphi \) does not contain any division operator, and let \(\mathcal {A}\) be the monitor computed using Algorithm 2. Suppose the size of \(\varphi \) is n. For a given upper bound on estimation error \(\overline{\varepsilon }\in \mathbb {R}\), the minimum number of visits to every state in \( Dom (V_{\varphi })\) for obtaining an output with error at most \(\overline{\varepsilon }\) and confidence at least \(1-\delta \) on any path is given by:

$$\begin{aligned} -\frac{(u_\varphi -l_\varphi )^2\ln \left( \frac{\delta }{2}\right) n}{2\overline{\varepsilon }^2}, \end{aligned}$$
(4)

where \([l_\varphi , u_\varphi ]\) is the set of possible values of \(\varphi \) for every valuation of every variable (having domain [0, 1]) in \(\varphi \).

The bound follows from the Hoeffding’s inequality, together with the fact that every dependent multiplication increments the required number of samples by 1. A similar bound for the general case with division is left open.

5 Bayesian Monitoring

Fix a problem instance \(\left( Q=[1. .N],\varphi ,\delta \right) \). Let \(\mathbb {M}=\varDelta (N-1)^{N}\) be the shorthand notation for the set of transition probability matrices of the Markov chains with state space \(Q\). Let \(p_\theta :\mathbb {M}\rightarrow [0,1]\) be the prior probability density function over \(\mathbb {M}\), which is assumed to be specified using the matrix beta distribution (the definition can be found in standard textbooks on Bayesian statistics [37, pp. 280]). Let \(\mathbb {1}\) be a matrix, with its size dependent on the context, whose every element is 1. We make the following common assumption [31, 37, p. 50]:

Assumption 1

(Prior). We are given a parameter matrix \(\theta \ge \mathbb {1}\), and \(p_\theta \) is specified using the matrix beta distribution with parameter \(\theta \). Moreover, the initial state of the Markov chain is fixed.

When \(\theta =\mathbb {1}\), then \(p_\theta \) is the uniform density function over \(\mathbb {M}\). After observing a path \(\vec {x}\), using Bayes’ rule we obtain the posterior density function \(p_\theta (\cdot \mid \vec {x})\), which is known to be efficiently computable due to the so-called conjugacy property that holds due to Assumption 1. From the posterior density, we obtain the expected posterior semantic value of \(\varphi \) as: \(\mathbb {E}_{\theta }(\varphi (M)\mid \vec {x}) {:}{=}\int _{\mathbb {M}} \varphi (M)\cdot p_{\theta }(M\mid \vec {x})dM\). The heart of our Bayesian monitor is an efficient incremental computation of \(\mathbb {E}_\theta (\varphi (M)\mid \vec {x})\)—free from numerical integration. Once we can compute \(\mathbb {E}_\theta (\varphi (M)\mid \vec {x})\), we can also compute the posterior variance \(S^2\) of \(\varphi (M)\) using the known expression \(S^2=\mathbb {E}_\theta (\varphi ^2(M)\mid \vec {x})-\mathbb {E}_\theta (\varphi (M)\mid \vec {x})\), which enables us to compute a confidence interval for \(\varphi (M)\) using the Chebyshev’s inequality. In the following, we summarize our procedure for estimating \(\mathbb {E}_\theta (\varphi (M)\mid \vec {x})\).

5.1 The Main Principle

The incremental computation of \(\mathbb {E}_\theta (\varphi (M)\mid \vec {x})\) is implemented in \(\texttt{BayesExpMonitor}\). We first transform the expression \(\varphi \) into the polynomial form \(\varphi '=\sum _l \kappa _l\xi _l\), where \(\lbrace \kappa _l\rbrace _l\) are the weights and \(\lbrace \xi _l\rbrace _l\) are monomials. If the size of \(\varphi \) is n then the size of \(\varphi '\) is \(\mathcal {O}(n2^{\frac{n}{2}})\). Then we can use linearity to compute the overall expectation as the weighted sum of expectations of the individual monomials: \(\mathbb {E}_\theta (\varphi (M)\mid \vec {x}) = \mathbb {E}_\theta (\varphi '(M)\mid \vec {x})=\sum _l \kappa _l\mathbb {E}_\theta (\xi _l(M)\mid \vec {x})\). In the following, we summarize the procedure for estimating \(\mathbb {E}_\theta (\xi (M)\mid \vec {x})\) for every monomial \(\xi \).

Let \(\xi \) be a monomial, and let \(\vec {x}ab\in Q^*\) be a sequence of states. We use \(d_{ij}\) to store the exponent of the variable \(v_{ij}\) in the monomial \(\xi \), and define \(d_a{:}{=}\sum _{j\in [1. .N]} d_{aj}\). Also, we record the sets of (i, j)-s and i-s with positive and negative \(d_{ij}\) and \(d_{i}\) entries: \(D_i^+{:}{=}\lbrace j\mid d_{ij}>0\rbrace \), \(D_i^-{:}{=}\lbrace j\mid d_{ij}<0\rbrace \), \(D^+{:}{=}\lbrace i\mid d_i>0\rbrace \), and \(D^-{:}{=}\lbrace i\mid d_i<0\rbrace \).

For any given word \(\vec {w}\in Q^*\), let \(c_{ij}({\vec {w}})\) denote the number of ij-s in \(\vec {w}\) and let \(c_{i}({\vec {w}}){:}{=}\sum _{j\in Q} c_{ij}({\vec {w}})\). Define \(\overline{c}_i({\vec {w}}){:}{=}c_i({\vec {w}}) + \sum _{j\in [1. .N]}\theta _{ij}\) and \(\overline{c}_{ij}({\vec {w}}){:}{=}c_{ij}({\vec {w}})+\theta _{ij}\). Let \(\mathcal {H}:Q^*\rightarrow \mathbb {R}\) be defined as:

$$\begin{aligned} \mathcal {H}(\vec {w}) {:}{=}\frac{ \prod _{i= 1}^N \prod _{j\in D_i^+} {}^{(\overline{c}_{ij}({\vec {w}})-1)+|d_{ij}|}P_{|d_{ij}|} }{ \prod _{i\in D^+} {}^{(\overline{c}_i({\vec {w}})-1)+|d_i|}P_{|d_i|} } \cdot \frac{ \prod _{i\in D^-}{}^{(\overline{c}_i({\vec {w}})-1)}P_{|d_i|} }{ \prod _{i= 1}^N\prod _{j\in D_i^-}{}^{(\overline{c}_{ij}({\vec {w}})-1)}P_{|d_{ij}|} }, \end{aligned}$$
(5)

where \({}^{n}P_{k}{:}{=}\frac{n!}{(n-k)!}\) is the number of permutations of \(k>0\) items from \(n>0\) objects, for \(k\le n\), and we use the convention that for \(S=\emptyset \), \(\prod _{s\in S} \ldots = 1\). Below, in Lemma 1, we establish that \(\mathbb {E}_\theta (\xi (M)\mid \vec {w}) = \mathcal {H}(\vec {w})\), and present an efficient incremental scheme to compute \(\mathbb {E}_\theta (\xi (M)\mid \vec {x}ab)\) from \(\mathbb {E}_\theta (\xi (M)\mid \vec {x}a)\).

Lemma 1

(Incremental computation of \(\mathbb {E}(\cdot \mid \cdot )\)). If the following consistency condition

$$\begin{aligned} \forall i,j\in [1. .N]\;.\; \overline{c}_{ij}({\vec {w}}) + d_{ij} > 0 \end{aligned}$$
(6)

is met, then the following holds:

$$\begin{aligned} \mathbb {E}(\xi (M)\mid \vec {x}ab)= \mathcal {H}(\vec {x}ab) = \mathcal {H}(\vec {x}a)\cdot \frac{\overline{c}_{ab}({\vec {x}})+d_{ab}}{\overline{c}_{ab}({\vec {x}})} \cdot \frac{\overline{c}_a({\vec {x}})}{\overline{c}_a({\vec {x}})+d_a}. \end{aligned}$$
(7)

Condition (6) guarantees that the permutations in (5) are well-defined. The first equality in (7) follows from Marchal et al. [51], and the rest uses the conjugacy of the prior. Lemma 1 forms the basis of the efficient update of our Bayesian monitor. Observe that on any given path, once (6) holds, it continues to hold forever. Thus, initially the monitor keeps updating \(\mathcal {H}\) internally without outputting anything. Once (6) holds, it keeps outputting \(\mathcal {H}\) from then on.

figure e

5.2 Implementation of the Bayesian Monitor

We present the Bayesian monitor implementation in \(\texttt{BayesConfIntMonitor}\) (Algorithm 4), which invokes \(\texttt{BayesExpMonitor}\) (Algorithm 3) as subroutine. \(\texttt{BayesExpMonitor}\) computes the expected semantic value of an expression \(\varphi \) in polynomial form, by computing the individual expected value of each monomial using Propostion 1, and combining them using the linearity property. We drop the arguments from \(\overline{c}_i(\cdot )\) and \(\overline{c}_{ij}(\cdot )\) and simply write \(\overline{c}_i\) and \(\overline{c}_{ij}\) as constants associated to appropriate words. The symbol \(m_{ij}\) in Line 5 of \( Init \) is used as a bookkee** variable for quickly checking the consistency condition (Eq. 6) in Line 5 of \( Next \). In \(\texttt{BayesConfIntMonitor}\), we compute the expected value and the variance of \(\varphi \), by invoking \(\texttt{BayesExpMonitor}\) on \(\varphi \) and \(\varphi ^2 \) respectively, and then compute the confidence interval using the Chebyshev’s inequality. It can be observed in the \( Next \) subroutines of \(\texttt{BayesConfIntMonitor}\) and \(\texttt{BayesExpMonitor}\) that a deterministic transition function suffices for the Bayesian monitors.

figure f

Theorem 4

(Correctness). Let \((Q,\varphi ,\delta )\) be a problem instance, and \(p_\theta \) be given as the prior distribution which satisfies Assumption 1. Algorithm 4 produces a monitor for \((Q,\varphi ,\delta )\) that solves Problem 2.

Theorem 5

Computational resources). Let \((Q,\varphi ,\delta )\) be a problem instance and \(\mathcal {A}\) be the monitor computed using the \(\texttt{BayesConfIntMonitor}\) routine of Algorithm 4. Suppose the size of \(\varphi \) is n. The monitor \(\mathcal {A}\) requires \(\mathcal {O}(n^22^n)\) registers, and takes \(\mathcal {O}(n^22^n)\) time to update its output after receiving a new input symbol. For the special case of \(\varphi \) being in polynomial form, \(\mathcal {A}\) requires only \(\mathcal {O}(n^2)\) registers, and takes only \(\mathcal {O}(n^2)\) time to update its output after receiving a new input symbol.

A bound on the convergence speed of the Bayesian monitor is left open. This would require a bound on the change in variance with respect to the length of the observed path, which is not known for the general case of PSEs. Note that the efficient (quadratic) cases are different for the frequentist and Bayesian monitors, suggesting the use of different monitors for different specifications.

6 Experiments

We implemented our frequentist and Bayesian monitors in a tool written in Rust, and used the tool to design monitors for the lending and the college admission examples taken from the literature [48, 54] (described in Sect. 1.1). The generators are modeled as Markov chains (see Fig. 1)—unknown to the monitors—capturing the sequential interactions between the decision-makers (i.e., the bank or the college) and their respective environments (i.e., the loan applicants or the students), as described by D’Amour et al. [16]. The setup of the experiments is as follows: We created a multi-threaded wrapper program, where one thread simulates one long run of the Markov chain, and a different thread executes the monitor. Every time a new state is visited by the Markov chain on the first thread, the information gets transmitted to the monitor on the second thread, which then updates the output. The experiments were run on a Macbook Pro 2017 equipped with a 2,3 GHz Dual-Core Intel Core i5 processor and 8GB RAM. The tool can be downloaded from the following url, where we have also included the scripts to reproduce our experiments: https://github.com/ista-fairness-monitoring/fmlib.

We summarize the experimental results in Fig. 3, and, from the table, observe that both monitors are extremely lightweight: they take less than a millisecond per update and small numbers of registers to operate. From the plots, we observe that the frequentist monitors’ outputs are always centered around the ground truth values of the properties, empirically showing that they are always objectively correct. On the other hand, the Bayesian monitors’ outputs can vary drastically for different choices of the prior, empirically showing that the correctness of outputs is subjective. It may be misleading that the outputs of the Bayesian monitors are wrong as they often do not contain the ground truth values. We reiterate that from the Bayesian perspective, the ground truth does not exist. Instead, we only have a probability distribution over the true values that gets updated after observing the generated sequence of events. The choice of the type of monitor ultimately depends on the application requirements.

Fig. 3.
figure 3

The plots show the \(95\%\) confidence intervals estimated by the monitors over time, averaged over 10 different sample paths, for the lending with demographic parity (left), lending with equalized opportunity (middle), and the college admission with social burden (right) problems. The horizontal dotted lines are the ground truth values of the properties, obtained by analyzing the Markov chains used to model the systems (unknown to the monitors). The table summarizes various performance metrics.

Full size image

7 Conclusion

We showed how to monitor algorithmic fairness properties on a Markov chain with unknown transition probabilities. Two separate algorithms are presented, using the frequentist and the Bayesian approaches to statistics. The performances of both approaches are demonstrated, both theoretically and empirically.

Several future directions exist. Firstly, more expressive classes of properties need to be investigated to cover a broader range of algorithmic fairness criteria. We believe that boolean logical connectives, as well as min and max operators can be incorporated straightforwardly using ideas from the related literature [3]. This also adds support for absolute values, since \(|x| = \max \lbrace x,-x\rbrace \). On the other hand, properties that require estimating how often a state is visited would require more information about the dynamics of the Markov chain, including its mixing time. Monitoring statistical hyperproperties [18] is another important direction, which will allow us to encode individual fairness properties [21]. Secondly, more liberal assumptions on the system model will be crucial for certain practical applications. In particular, hidden Markov models, time-inhomogeneous Markov models, Markov decision processes, etc., are examples of system models with widespread use in real-world applications. Finally, better error bounds tailored for specific algorithmic fairness properties can be developed through a deeper mathematical analysis of the underlying statistics, which will sharpen the conservative bounds obtained through off-the-shelf concentration inequalities.