Concepts in Magnetism

Abstract

I review some general concepts in magnetism including the nature of magnetic exchange (direct, indirect and superexchange), and how exchange interactions play out in multiple spin systems. The nature of atomic orbitals and the way in which they interact with the spin system is also considered. Several examples are also treated, including the Jahn–Teller interaction and its role in the properties in layered manganites.

2.1 Introduction

Magnetic properties are found in a wide variety of materials. In order to explain magnetism we need to consider a range of different behaviours in many different types of magnetic system. Consider the following: Fe and Ni are both metallic elements and exhibit ferromagnetism; MnO is an insulating oxide with a three-dimensional antiferromagnetic structure; La$_2$CuO$_4$ is a layered material which exhibits antiferromagnetism but, when doped, becomes superconducting; some compounds do not order magnetically but show frustrated effects with an abundance of slow dynamics; some molecules become single-molecule magnets in which the individual molecules show quantum tunnelling of magnetization and a range of other interesting properties. Theories of magnetism have to explain all these materials and more.

For a start, we must realize that a classical approach will not work. The Bohr–van Leeuwen theorem [1] states that in a classical system there is no thermal equilibrium magnetization. We can prove this in outline as follows: in classical statistical mechanics the partition function Z for N particles, each with charge q, is proportional to

$$\begin{aligned} \int \int \cdots \int \exp \left[ -\beta E(\{ \varvec{r}_i,\varvec{p}_i\}\right] \,\,\mathrm{d}\varvec{r}_1\cdots \mathrm{d}\varvec{r}_N\,\,\mathrm{d}\varvec{p}_1\cdots \mathrm{d}\varvec{p}_N \;, \end{aligned}$$

(2.1)

where $\beta =1/k_\mathrm{B}T$, $k_\mathrm{B}$ is the Boltzmann constant, T is the temperature and $i=1,\ldots ,N$. Here $E(\{ \varvec{r}_i,\varvec{p}_i \})$ is the energy associated with the N charged particles having positions $\varvec{r}_1$, $\varvec{r}_2$, $\ldots , \varvec{r}_N$, and momenta $\varvec{p}_1$, $\varvec{p}_2$, $\ldots , \varvec{p}_N$. The integral is, therefore, over a 6N-dimensional phase space (3N position coordinates, 3N momentum coordinates). The effect of a magnetic field is to shift the momentum of each particle by an amount $q\varvec{A}$. We must, therefore, replace $\varvec{p}_i$ by $\varvec{p}_i -q\varvec{A}$. The limits of the momentum integrals go from $-\infty$ to $+\infty$ so this shift can be absorbed by shifting the origin of the momentum integrations. Hence the partition function is not a function of magnetic field, and so neither is the free energy $F=-k_\mathrm{B}T \log {Z}$. Thus the magnetic moment $m=-(\partial F/\partial B)_T$ must be zero in a classical system.

Thus, we need quantum mechanics to make further progress. In this chapter, I will not provide an exhaustive review of magnetism (fuller treatments can be found elsewhere, e.g. [2,3,4,5]) but focus on a few key issues and some selected examples. To begin our discussion, it is helpful to note the energy scales inherent in magnetic problems. First, there is the kinetic energy which is on the eV scale. This typically takes a value like $\hbar ^2\pi ^2/(2mL^2$), where L is a length scale and this expression is the familiar one for particle in a box. This is an energy cost and arises because it takes energy to put an electron in a small box. Second comes the potential energy which is also on a similar scale and takes a form such as $e^2/(4\pi \epsilon _0L)$. This will be a negative energy if considering the attraction between an electron and a nucleus (and becomes larger and more negative as L decreases) and positive if considering electron–electron repulsion. Atoms are the size they are because of a compromise between kinetic energy wanting the atom to be infinite size and the potential energy wanting the atom to be zero size. Because one energy goes as $L^{-2}$ and the other as $-L^{-1}$ a compromise can be reached (and this is essentially the derivation of the Bohr radius). Both the kinetic and potential energies are large and are typically $\gg k_\mathrm{B}T$. Next, we have to add the spin–orbit interaction which is typically much smaller, usually in the meV, and the magnetocrystalline anisotropy, which in cubic materials is in the $\upmu$eV. These effects will turn out to be very important in magnetic materials, but they are small perturbations to the main interactions and will mainly come into play only once the magnetic order is established by the dominant interactions.

2.2 Exchange

The exchange interaction arises from the kinetic and potential energy in bonds between atoms. To see how this comes about, we begin by recalling simple results for the molecular orbitals in H$_2$ [see Fig. 2.1a]. We label the two hydrogen atoms A and B and write the wave function $\vert \psi \rangle$  as a linear combination of atomic orbitals $\vert \psi _\mathrm{A}\rangle$ and $\vert \psi _\mathrm{B}\rangle$ so that 

$$\begin{aligned} \vert \psi \rangle = c_\mathrm{A} \vert \psi _\mathrm{A}\rangle + c_\mathrm{B} \vert \psi _\mathrm{B}\rangle \;. \end{aligned}$$

(2.2)

The Hamiltonian can be written as a sum of the kinetic energy and two terms for the potential energy due to the attraction to each hydrogen nucleus so that

$$\begin{aligned} \hat{\mathcal{H}}=-{\hbar ^2\over 2m}\nabla ^2 + V_\mathrm{A} + V_\mathrm{B} \;. \end{aligned}$$

(2.3)

We then need to solve the equation $\hat{\mathcal{H}}\vert \psi \rangle = E\vert \psi \rangle$. The diagonal integral $E_0$, which can be approximated by the binding energy of the electron at one of the centres for a hydrogen atom, is given by

$$\begin{aligned} E_0 = \langle \psi _\mathrm{A}\vert \hat{\mathcal{H}}\vert \psi _\mathrm{A}\rangle \;. \end{aligned}$$

(2.4)

The transfer integral (also known as the hop** integral or resonance integral) t is given by

$$\begin{aligned} t = \langle \psi _\mathrm{A}|\hat{\mathcal{H}}|\psi _\mathrm{B}\rangle \;. \end{aligned}$$

(2.5)

Fig. 2.1

a Two hydrogen atoms A and B can lower their energy by forming a hydrogen molecule H$_2$. b The bonding and antibonding molecular orbitals $\sigma$ and $\sigma ^*$

In the simplest approximation (the Hückel approximation), the overlap integrals are given by $S_{ij}=\langle \psi _i|\psi _j\rangle =\delta _{ij}$ and hence the secular equation $|H_{ij}-ES_{ij}|=0$ can be written as

$$\begin{aligned} \left| \begin{matrix} E_0 -E &{} t \\ t &{} E_0-E \end{matrix} \right| = 0 \;, \end{aligned}$$

(2.6)

and hence

$$\begin{aligned} E=E_0\pm t \;. \end{aligned}$$

(2.7)

The eigenfunctions for these solutions are the symmetric solution

$$\begin{aligned} \vert \sigma \rangle = { \vert \psi _\mathrm{A} \rangle + \vert \psi _\mathrm{B}\rangle \over \sqrt{2} } \end{aligned}$$

(2.8)

which  costs energy $E_0-t$ and the antisymmetric solution

$$\begin{aligned} \vert \sigma ^*\rangle = { \vert \psi _\mathrm{A} \rangle - \vert \psi _\mathrm{B}\rangle \over \sqrt{2} } \end{aligned}$$

(2.9)

which costs energy $E_0+t$. These are known as the bonding and antibonding states, respectively [see Fig. 2.1b]. The hydrogen molecule has two electrons so the $\sigma$ level is full and the $\sigma ^*$ level is empty, thus saving the energy overall and leading to the H$_2$ molecule being a stable entity. The molecule He$_2$ does not form because it has four electrons and would, therefore, involve filling both $\sigma$ and $\sigma ^*$ and thus saves no energy (and in fact, outside the Hückel approximation, it turns out that $\sigma ^*-E_0 > E_0-\sigma$ and so helium bonding costs more energy than it saves).

2.2.1 Direct Exchange

Exchange interactions are nothing more than a consequence of electrostatic interactions and the familiar interplay between potential energy and kinetic energy that we see in chemical bonds. Consider a simple model with just two electrons which have spatial coordinates $\varvec{r}_1$ and $\varvec{r}_2$, respectively. The wave function for the joint state can be written as a product of single electron states, so that if the first electron is in state $\psi _a(\varvec{r}_1)$ and the second electron is in state $\psi _b(\varvec{r}_2)$, then the joint wave function is $\psi _a(\varvec{r}_1)\psi _b(\varvec{r}_2)$. However, this product state does not obey exchange  symmetry, since if we exchange the two electrons we get $\psi _a(\varvec{r}_2)\psi _b(\varvec{r}_1)$, which is not a multiple of what we started with. Therefore, the only states which we are allowed to make are symmetrized or antisymmetrized product states which behave properly under the operation of particle exchange.

For electrons, the overall wave function must be antisymmetric so the spin part of the wave function must either be an antisymmetric singlet state $\chi _\mathrm{S}$ ($S=0$) in the case of a symmetric spatial state or a symmetric triplet state $\chi _\mathrm{T}$ ($S=1$) in the case of an antisymmetric spatial state. Therefore, we can write the wave function for the singlet case $\Psi _\mathrm{S}$ and the triplet case $\Psi _\mathrm{T}$ as 

$$\begin{aligned} \Psi _\mathrm{S}= & {} {1 \over \sqrt{2}} [ \psi _a(\varvec{r}_1)\psi _b(\varvec{r}_2) + \psi _a(\varvec{r}_2)\psi _b(\varvec{r}_1)] \,\chi _\mathrm{S} \nonumber \\ \Psi _\mathrm{T}= & {} {1 \over \sqrt{2}} [ \psi _a(\varvec{r}_1)\psi _b(\varvec{r}_2) - \psi _a(\varvec{r}_2)\psi _b(\varvec{r}_1)] \,\chi _\mathrm{T} \;, \end{aligned}$$

(2.10)

where both the spatial and spin parts of the wave function are included. The energies of the two possible states are

$$\begin{aligned} E_\mathrm{S}= & {} \int \Psi _\mathrm{S}^* \hat{\mathcal{H}} \Psi _\mathrm{S} \,\mathrm{d}\varvec{r}_1\,\mathrm{d}\varvec{r}_2 \nonumber \\ E_\mathrm{T}= & {} \int \Psi _\mathrm{T}^* \hat{\mathcal{H}} \Psi _\mathrm{T} \,\mathrm{d}\varvec{r}_1\,\mathrm{d}\varvec{r}_2 \;, \nonumber \end{aligned}$$

with the assumption that the spin parts of the wave function $\chi _\mathrm{S}$ and $\chi _\mathrm{T}$ are normalized. The difference between the two energies is

$$\begin{aligned} E_\mathrm{S}-E_\mathrm{T} = 2\int \psi _a^*(\varvec{r}_1)\psi ^*_b(\varvec{r}_2) \hat{\mathcal{H}} \psi _a(\varvec{r}_2)\psi _b(\varvec{r}_1) \,\mathrm{d}\mathbf{r}_1\,\mathrm{d}\varvec{r}_2 \;. \end{aligned}$$

(2.11)

For a singlet state $\varvec{S_1}\cdot \varvec{S_2}=-\frac{3}{4}$ while for a triplet state $\varvec{S_1}\cdot \varvec{S_2}=\frac{1}{4}$. Hence the Hamiltonian can be written in the form of an ‘effective Hamiltonian’

$$\begin{aligned} \hat{\mathcal{H}} ={1 \over 4}(E_\mathrm{S}+3E_\mathrm{T})-(E_\mathrm{S}-E_\mathrm{T})\varvec{S}_1\cdot \varvec{S}_2 \;. \end{aligned}$$

(2.12)

This is the sum of a constant term and a term which depends on spin. The constant can be absorbed into other constant energy terms, but the second term is more interesting. The exchange constant J is defined by

$$\begin{aligned} J={E_\mathrm{S}-E_\mathrm{T} \over 2} = \int \psi _a^*(\varvec{r}_1)\psi ^*_b(\varvec{r}_2) \hat{\mathcal{H}} \psi _a(\varvec{r}_2)\psi _b(\varvec{r}_1) \,\mathrm{d}\mathbf{r}_1\,\mathrm{d}\varvec{r}_2 \;, \end{aligned}$$

(2.13)

and hence the spin-dependent term in the effective Hamiltonian can be written as

$$\begin{aligned} \hat{\mathcal{H}}^\mathrm{spin}=-2J\varvec{S_1}\cdot \varvec{S_2} \;. \end{aligned}$$

(2.14)

If $J>0$, $E_\mathrm{S}>E_\mathrm{T}$ and the triplet state $S=1$ is favoured. If $J<0$, $E_\mathrm{S}<E_\mathrm{T}$ and the singlet state $S=0$ is favoured. Thus, the exchange interaction compares two different configurations that are tied to the singlet and triplet spin states, but the energy difference associated with exchange comes from the difference in those two configurations worked out from an integral [see (2.13)] over the spatial coordinates. Thus the spins are really there just to label the two different spatial states and are inextricably tied to the spatial wave functions by the Pauli principle; the exchange interaction is really between spatial wave functions, even though we tend to think about it as between the spin parts that really just come along for the ride!

Equation (2.14) is relatively simple to derive for two electrons, but generalizing to a many-body system is far from trivial. It motivates the Hamiltonian of the Heisenberg model:

$$\begin{aligned} \hat{\mathcal{H}}=-\sum _{ij}J_{ij}\varvec{S}_i\cdot \varvec{S}_j \;, \end{aligned}$$

(2.15)

where $J_{ij}$ is the exchange constant between the ith and jth spins. The factor of 2 is omitted because the summation includes each pair of spins twice. Another way of writing (2.15) is

$$\begin{aligned} \hat{\mathcal{H}}=-2\sum _{i>j}J_{ij}\varvec{S}_i\cdot \varvec{S}_j \;, \end{aligned}$$

(2.16)

where the $i>j$ avoids the ‘double-counting’ and hence the factor of two returns. It is worth noting that there are different conventions for the definition of J that are in use in the literature. I call these the J-convention and the 2J-convention and they are summarized in Fig. 2.2. Note that it is also possible to choose the sign of J so that $J>0$ means ferromagnetic (as here) or antiferromagnetic. Both choices are found in the literature.

Fig. 2.2

The two different conventions used for the definition of J. In this chapter (and in [2]), we are using the 2J convention (so that 2J is the energy associated with a single pairwise interaction between two spins). The various alternative expressions that one can use for the Heisenberg interaction are shown under the heading ‘many spins’, as well as an expression for a one-dimensional (1D) chain of spins

2.2.2 Indirect Exchange

If the electrons on neighbouring magnetic atoms interact via an exchange interaction, this is known as direct exchange. This is because the exchange interaction proceeds directly without the need for an intermediary, and this was considered in the previous section.

Very often direct exchange cannot be an important mechanism in controlling the magnetic properties because there is insufficient direct overlap between neighbouring magnetic orbitals. For example, in rare earths the 4f electrons are strongly localized and lie very close to the nucleus, with little probability density extending significantly further than about a tenth of the interatomic spacing. This means that the direct exchange interaction is unlikely to be very effective in rare earths. Even in transition metals, such as Fe, Co and Ni, where the 3d orbitals extend further from the nucleus, it is extremely difficult to justify why direct exchange should lead to the observed magnetic properties. These materials are metals which means that the role of the conduction electrons should not be neglected, and a correct description needs to be taken into account of both the localized and band character of the electrons.

In metals the exchange interaction between magnetic ions can be mediated by the conduction electrons. A localized magnetic moment spin-polarizes the conduction electrons and this polarization in turn couples to a neighbouring localized magnetic moment a distance r away. The exchange interaction is thus indirect because it does not involve direct coupling between magnetic moments. It is known as the RKKY interaction (or also as itinerant exchange). The name RKKY is used because of the initial letters of the surnames of the discoverers of the effect, Ruderman, Kittel, Kasuya and Yosida [6,7,8]. The coupling takes the form of an r-dependent exchange interaction $J_\mathrm{RKKY}(r)$ given by

$$\begin{aligned} J_\mathrm{RKKY}(r) \propto \displaystyle { {\cos (2k_\mathrm{F}r) \over r^3 }} \;, \end{aligned}$$

(2.17)

at large r (assuming a spherical Fermi surface of radius $k_\mathrm{F}$). The interaction is long range and has an oscillatory dependence on the distance between the magnetic moments (see Fig. 2.3). Hence depending on the separation it may be either ferromagnetic or antiferromagnetic. The coupling is oscillatory with wavelength $\pi /k_\mathrm{F}$ because of the sharpness of the Fermi surface.

Fig. 2.3

The real space susceptibility of a free electron gas is given by $\chi (r)=2k_\mathrm{F}^3\mu _0\mu _\mathrm{B}^2 g(E_\mathrm{F})F(2k_\mathrm{F}r)/\pi$ where $F(x)=(-x\cos x + \sin x )/x^4$ is the function illustrated. A localized spin in a free electron gas, therefore, gives rise to an effective exchange $J_\mathrm{RKKY} \propto F(2k_\mathrm{F}r)$ and this is proportional to $\cos (2k_\mathrm{F}r)/r^3$ when $r\gg k_\mathrm{F}^{-1}$

2.2.3 Superexchange

A number of ionic solids, including some oxides and fluorides, have magnetic ground states. For example, MnO [see Fig. 2.4a] and MnF$_2$ are both antiferromagnets, though this observation appears at first sight rather because there is no direct overlap between the electrons on Mn$^{2+}$ ions in each system. The exchange interaction is normally very short ranged so that the longer ranged interaction that is operating in this case must be in some sense ‘super’ (think of Superman lea** over buildings, a skill not afforded to ordinary mortals).

Fig. 2.4

a The crystal structure of MnO. Nearest neighbour pairs of Mn$^{2+}$ (manganese) ions are connected via O$^{2-}$ (oxygen) ions. b A simple model of superexchange for a Mn–O–Mn bond. I: the antiferromagnetic ground state with opposite spins on the two Mn ions and a pair of electrons on the oxygen anion. II and III: two excited states of the antiferromagnetic ground state in which the electrons from (I) hop back and forth. IV: the competing ferromagnetic ground state. This is energetically more costly because the excited states analogous to (II) and (III) are not available because of the Pauli exclusion principle

The origin of superexchange is the possibility of mixing in excited states to lower the energy. The favouring of antiferromagnetic superexchange in a linear Mn–O–Mn bond arises from the fact that the excited states are allowed, while for the ferromagnetic arrangement these excited states are forbidden [see Fig. 2.4b]. One can consider this problem with a toy model based on a Hubbard-style Hamiltonian (see, e.g. [9]) which may be written as

$$\begin{aligned} \hat{\mathcal{H}} = -t\sum _{\langle i j\rangle \sigma } \hat{c}^{\dagger }_{i \sigma } \hat{c}_{j \sigma } + U \sum _{i} \hat{n}_{i \uparrow } \hat{n}_{i \downarrow } \;, \end{aligned}$$

(2.18)

where the first sum is over nearest neighbours; thus energy is lowered by hop** (the first term on the right) but there is an energy penalty for double occupancy (the second term on the right) due to the Coulomb repulsion energy U. Let us now restrict this model to a system with two possible sites for electrons (here we are ignoring the intermediate oxygen to for simplicity). We can start by putting a single electron with spin $\uparrow$ into the system. Using a basis $\vert \!\uparrow ,0\rangle$ and $\vert 0,\uparrow \rangle$, the Hamiltonian is given by

$$\begin{aligned} \hat{\mathcal{H}} = \left( \begin{array}{cc} 0 &{} -t\\ -t &{} 0\\ \end{array} \right) \;, \end{aligned}$$

(2.19)

because with one electron there is no possibility of a Coulomb penalty, and so the only energy to worry about is the energy saving you get from hop**. This is the same as the H$_2$ problem we considered earlier and the eigenvalues are $\pm t$ and so the lowest energy state is the bonding state, just as before.

Now let us put a second electron into the system with opposite spin to the first. Now using a basis such that a general state can be written as

$$\begin{aligned} \vert \psi \rangle = a \vert \!\uparrow \downarrow ,0 \rangle + b\vert \!\uparrow ,\downarrow \rangle +c\vert \!\downarrow ,\uparrow \rangle + d \vert 0,\uparrow \downarrow \rangle \;, \end{aligned}$$

(2.20)

and we can easily show that in this basis the Hubbard Hamiltonian is 

$$\begin{aligned} \hat{\mathcal{H}}= \left( \begin{array}{cccc} U &{} t &{} -t &{} 0\\ t &{} 0 &{} 0 &{} t\\ -t &{} 0 &{} 0 &{} -t\\ 0 &{} t &{} -t &{} U \end{array} \right) \;, \end{aligned}$$

(2.21)

where the minus signs appear because of the exchange symmetry. The eigenvalues are 0, U and $(U/2)\pm \sqrt{(U/2)^2+2t^2}$, so in the limit that $t/U\ll 1$ the last pair of eigenvalues are $U+2t^2/U+O(t^4/U^3)$ and $-2t^2/U+O(t^4/U^3)$. Thus, the ground state has energy $-2t^2/U$. If we try the same problem again with two electrons with the same spin then they cannot sit on the same site because of the Pauli exclusion principle. Thus the only state possible is $\vert \!\uparrow , \uparrow \rangle$ and this has energy $E=0$. Thus, there is an energy saving in having the two electrons with opposite spin because you can go lower than $E=0$ and have $E=-2t^2/U+O(t^4/U^3)$. This means that the exchange interaction has a magnitude $J \approx 2t^2/U$. The moral of the story is that by having the possibility to mix in the higher energy states in which two spins sit on the same site (costing U), it is possible to lower the overall energy. The antiferromagnetic arrangement allows this process to happen; the ferromagnetic arrangement forbids it. Superexchange can be considered in more detail [10] and can in certain circumstances be ferromagnetic. The size and sign of the superexchange interaction is codified in the Goodenough–Kanamori–Anderson rules [11,12,13,14]. 

2.3 Consequences of the Heisenberg Exchange Interaction

We have seen that at the heart of the exchange interaction is a term $\hat{\varvec{S}}_a \cdot \hat{\varvec{S}}_b$, a simple scalar product between two spin operators. If that scalar product is expanded, we have

$$\begin{aligned} \hat{\varvec{S}}_a \cdot \hat{\varvec{S}}_b = \hat{S}^x_a \hat{S}^x_b + \hat{S}^y_a \hat{S}^y_b + \hat{S}^z_a \hat{S}^z_b = \hat{S}^z_a \hat{S}^z_b + \frac{1}{2}( \hat{S}^+_a \hat{S}^-_b + \hat{S}^-_a \hat{S}^+_b ) \;, \end{aligned}$$

(2.22)

where the raising and lowering operators $\hat{S}^+$ and $\hat{S}^-$ are defined by

$$\begin{aligned} \hat{S}^+= & {} \hat{S}^x+\mathrm{i}\hat{S}^y \nonumber \\ \hat{S}^-= & {} \hat{S}^x-\mathrm{i}\hat{S}^y \;. \end{aligned}$$

(2.23)

Although the term $\hat{S}^z_a \hat{S}^z_b$ in (2.22) seems to be simple enough to handle, the term $\frac{1}{2}( \hat{S}^+_a \hat{S}^-_b + \hat{S}^-_a \hat{S}^+_b )$ will give rise to flip-flop processes in which simultaneously an up-spin labelled a is lowered and a down-spin labelled b is raised, or vice versa. This part of the interaction has profound effects.

2.3.1 Two Interacting Spin-$\frac{1}{2}$ Particles

In this section, we will consider two spin-$\frac{1}{2}$ particles coupled by a scalar interaction described by a Hamiltonian $\hat{\mathcal{H}} = A \hat{\varvec{S}}_a \cdot \hat{\varvec{S}}_b$, where $\hat{\varvec{S}}_a$ and $\hat{\varvec{S}}_b$ are the operators for the spins for the two particles. We can also write the total spin operator $\hat{\varvec{S}}^\mathrm{tot}= \hat{\varvec{S}}_a + \hat{\varvec{S}}_b$ so that

$$\begin{aligned} (\hat{\varvec{S}}^\mathrm{tot})^2 = (\hat{\varvec{S}}_a)^2 + (\hat{\varvec{S}}_b)^2 + 2\hat{\varvec{S}}_a \cdot \hat{\varvec{S}}_b \;. \end{aligned}$$

(2.24)

In quantum mechanics, when you combine the angular momentum of two spin-$\frac{1}{2}$ particles you have the ‘addition law’ that $\frac{1}{2}+\frac{1}{2} = 0,1$. You can think of this simply as arising from the fact that you can combine the two moments together constructively or destructively. Alternatively, imagine adding two classical vectors $\varvec{J}_1$ and $\varvec{J}_2$ together but varying the angle between them. In that case, the resulting vector $\varvec{J}_1+\varvec{J}_2$ would have length ranging from $|J_1-J_2|$ to $J_1+J_2$ (where $J_1=|\varvec{J}_1|$ and $J_2=|\varvec{J}_2|$). More formally, combining the representations of two spin-$\frac{1}{2}$ together yields a representation

$$\begin{aligned} D^{(\frac{1}{2})}\otimes D^{(\frac{1}{2})} = D^{(0)}\oplus D^{(1)} \;. \end{aligned}$$

(2.25)

In other words, the result of combining two spin-$\frac{1}{2}$ particles is a combined object with spin quantum number $s=0$ or 1. The eigenvalue of $(\hat{\varvec{S}}^\mathrm{tot})^2$ is $s(s+1)$ which is therefore either 0 or 2 for the cases of $s=0$ or 1. The eigenvalues of both $(\hat{\varvec{S}}_a)^2$ and $(\hat{\varvec{S}}_b)^2$ are $\frac{3}{4}$. Hence from (2.24)

$$\begin{aligned} \hat{\varvec{S}}_a \cdot \hat{\varvec{S}}_b = \left\{ \begin{matrix} +\frac{1}{4} &{} \mathrm{if} &{} s=1 \\ -\frac{3}{4} &{} \mathrm{if} &{} \ \ s=0 \;. \end{matrix} \right. \end{aligned}$$

(2.26)

The system, therefore, has two energy levels for $s=0$ and 1 with energies given by

$$\begin{aligned} E = \left\{ \begin{matrix} +\frac{A}{4} &{} \mathrm{if} &{} s=1 \\ -\frac{3A}{4} &{} \mathrm{if} &{} \ \ s=0 \;. \end{matrix} \right. \end{aligned}$$

(2.27)

The degeneracy of each state is $2s+1$, so that the $s=0$ state is a singlet (a single energy level) and the $s=1$ state is a triplet (three energy levels). The z component of the spin of this state, $m_s$, can only equal 0 for the singlet, but can be $-1$, 0, or 1 for the triplet. Thus the product of two spin-$\frac{1}{2}$ representations, which have a dimensionality of $2\times 2=4$, gives rise to states $s=0$ (singlet) and $s=1$ (triplet), which have a total dimensionality of $1+3=4$.

Table 2.1 The eigenstates of $\hat{\varvec{S}}_a \cdot \hat{\varvec{S}}_b$ for a two-spin system and the corresponding values of $m_s$, s and the eigenvalue of $\hat{\varvec{S}}_a \cdot \hat{\varvec{S}}_b$

We have considered the eigenvalues of $\hat{\varvec{S}}_a \cdot \hat{\varvec{S}}_b$, but what about the eigenstates? The most straightforward basis to consider is

$$\begin{aligned} \vert \!\uparrow \uparrow \rangle \;, \quad \vert \!\uparrow \downarrow \rangle \;, \quad \vert \!\downarrow \uparrow \rangle \;, \quad \vert \!\downarrow \downarrow \rangle \;. \end{aligned}$$

(2.28)

The first arrow refers to the z component of the spin labelled a and the second arrow refers to the z component of the spin labelled b. The eigenstates of $\hat{\varvec{S}}_a \cdot \hat{\varvec{S}}_b$ are linear combinations of these basis states and are listed in Table 2.1. The value of $m_s$ is equal to the sum of the z components of the individual spins. Since the eigenstates are a mixture of states in the original basis, we cannot know both the z components of the original spins and the total spin of the resultant entity. This is a general feature which will become more important in more complicated situations.

The basis in (2.28) also fails to satisfy the condition that the overall wave function must be antisymmetric with respect to exchange of the two electrons. Since the wave function is a product of a spatial function $\psi _\mathrm{space}(\varvec{r}_1, \varvec{r}_2)$ and the spin function $\chi$, the spatial wave function can be either symmetric or antisymmetric with respect to exchange of electrons. For example, the spatial wave function

$$\begin{aligned} \psi _\mathrm{space}(\varvec{r}_1, \varvec{r}_2) = { \phi (\varvec{r}_1)\xi (\varvec{r}_2) \pm \phi (\varvec{r}_2)\xi (\varvec{r}_1) \over \sqrt{2} } \end{aligned}$$

(2.29)

is symmetric ($+$) or antisymmetric (−) with respect to exchange of electrons depending on the ±. This type of symmetry is known as exchange symmetry. In (2.29), $\phi (\varvec{r}_i)$ and $\xi (\varvec{r}_i)$ are single-particle wave functions for the ith electron. Whatever is the exchange symmetry of the spatial wave function, the spin-wave function $\chi$ must have the opposite exchange symmetry. Hence $\chi$ must be antisymmetric when the spatial wave function is symmetric and vice versa. This is in order that the product $\psi _\mathrm{space}(\varvec{r}_1, \varvec{r}_2) \times \chi$ is antisymmetric overall.

States such as $\vert \!\uparrow \uparrow \rangle$ and $\vert \!\downarrow \downarrow \rangle$ are clearly symmetric under exchange of electrons, but exchanging the two electrons in $\vert \!\uparrow \downarrow \rangle$ yields $\vert \!\downarrow \uparrow \rangle$ which is not a multiple of $\vert \!\uparrow \downarrow \rangle$. Thus $\vert \!\uparrow \downarrow \rangle$, and also by an identical argument $\vert \!\downarrow \uparrow \rangle$, are both neither symmetric nor antisymmetric under exchange of the two electrons. The true eigenstates must, therefore, be linear combinations of these two states (see Table 2.1). The state $(\vert \!\uparrow \downarrow \rangle + \vert \!\downarrow \uparrow \rangle )/\sqrt{2}$ is symmetric under exchange of electrons (in common with the other two $s=1$ states) while the state $(\vert \!\uparrow \downarrow \rangle - \vert \!\downarrow \uparrow \rangle )/\sqrt{2}$ (the $s=0$ state) is antisymmetric under exchange of electrons.

Fig. 2.5

The energy levels for the two Hamiltonians: $\hat{\mathcal {H}}=A \hat{S}^z_a \hat{S}^z_b$ and $\hat{\mathcal {H}}=A \hat{\varvec{S}}_a \cdot \hat{\varvec{S}}_b$

The energy levels are shown in Fig. 2.5. Without the flip-flop term $\frac{1}{2}( \hat{S}^+_a \hat{S}^-_b + \hat{S}^-_a \hat{S}^+_b )$ in (2.22), the Hamiltonian is simply $\hat{\mathcal{H}}=A \hat{S}^z_a \hat{S}^z_b$ and this leads to two degenerate doublets as shown. The upper doublet (consisting of the states $\vert \!\uparrow \uparrow \rangle$ and $\vert \!\downarrow \downarrow \rangle$) is unchanged when the flip-flop terms are switched on. The lower doublet (consisting of the states $\vert \!\uparrow \downarrow \rangle$ and $\vert \!\downarrow \uparrow \rangle$, although strictly speaking it should of course be the symmetric and antisymmetric combinations of these two states) splits with the addition of the flip-flop terms to make $\hat{\mathcal {H}}=A \hat{\varvec{S}}_a \cdot \hat{\varvec{S}}_b$ and the symmetric combination rises up in energy to A/4 and the antisymmetric combination is lowered to $-3A/4$, becoming the ground state when $A>0$.

2.3.2 A Chain of Spins

Let us now consider not just two spins but a one-dimensional ferromagnetic chain of spin-$\frac{1}{2}$ moments described by the Heisenberg model. In one dimension, the Hamiltonian for the Heisenberg model can be written as

$$\begin{aligned} \hat{\mathcal{H}} = -2J\sum _i \left[ \hat{S}_i^z\hat{S}_{i+1}^z + {1 \over 2} (\hat{S}_i^+\hat{S}_{i+1}^- +\hat{S}_i^- \hat{S}_{i+1}^+) \right] \;, \end{aligned}$$

(2.30)

where $J>0$. The ground state $\Phi$ consists of all spins aligned [see Fig. 2.6a] and this is an eigenstate of $\hat{\mathcal{H}}$ so that $\hat{\mathcal{H}}\vert \Phi \rangle = -NS^2J\vert \Phi \rangle$.

Fig. 2.6

a The ground state of a one-dimensional ferromagnet in the Heisenberg model is $|\Phi \rangle$. An excited state $|j\rangle$ has a single flipped spin at site j. The spin-wave state $|q\rangle$ is a delocalized spin flip. b The dispersion relation for the spin waves

Now to create an excitation, let us flip a spin at site j, so let us now consider a state

$$\begin{aligned} \vert j \rangle = \hat{S}_j^-\vert \Phi \rangle \end{aligned}$$

(2.31)

which is simply the ground state with the spin at site j flipped [see Fig. 2.6a]. By flip** a spin, we have changed the total spin of the system by $\frac{1}{2}-(-\frac{1}{2})=1$. This excitation, therefore, has integer spin and is a boson. If we apply the Hamiltonian to this new state, we get

$$\begin{aligned} \hat{\mathcal{H}}\vert j \rangle = 2 \left[ (-NS^2 J + 2SJ) \vert j \rangle - SJ \vert j+1 \rangle - SJ \vert j-1 \rangle \right] \;, \end{aligned}$$

(2.32)

which is not a constant multiplied by $\vert j \rangle$, so this state is not an eigenstate of the Hamiltonian. Nevertheless, we can diagonalize the Hamiltonian by looking for plane wave solutions of the form

$$\begin{aligned} \vert q \rangle = {1 \over \sqrt{N} } \sum _j \mathrm{e}^{\mathrm{i}qR_j} \vert j \rangle \;. \end{aligned}$$

(2.33)

The state $\vert q \rangle$ is essentially a flipped spin delocalized (smeared out) across all the sites [see Fig. 2.6a] and is known as a spin wave or a magnon.   The state $|q\rangle$ is also an eigenstate of an operator exchanging any two spins, which is not the case for $|j\rangle$. Since $|q\rangle$ is a linear combination of states like $|j\rangle$ which represent a single flipped spin, the total spin in the z-direction of $\vert q\rangle$ itself has the value $NS-1$. It is then straightforward to show that

$$\begin{aligned} \hat{\mathcal{H}} \vert q \rangle = E(q) \vert q \rangle \;, \end{aligned}$$

(2.34)

where

$$\begin{aligned} E(q) = -2NS^2J + 4J S(1-\cos qa) \;. \end{aligned}$$

(2.35)

The energy of the excitation is then $\hbar \omega = 4J S(1-\cos qa)$ and is plotted in Fig. 2.6b. At small q, $\hbar \omega \approx 2J Sq^2a^2$, so that $\omega \propto q^2$. In three dimensions, the density of states is given by $g(q)\,\mathrm{d}q \propto q^2\,\mathrm{d}q$, which leads to

$$\begin{aligned} g(\omega )d\omega \propto \omega ^{1/2}\,\mathrm{d}\omega \end{aligned}$$

(2.36)

at low temperature where only small q and small $\omega$ are important. The spin waves are quantized in the same way as lattice waves. The latter are termed phonons, and so in the same way the former are termed magnons. They are bosons and have a spin of one.

The number of magnon modes excited at temperature T, $n_\mathrm{magnon}$, is calculated by integrating the magnon density of states over all frequencies after multiplying by the Bose factor,  $[\exp (\hbar \omega /k_\mathrm{B}T)-1]^{-1}$, which must be included because magnons are bosons. Thus the result is given by

$$\begin{aligned} n_\mathrm{magnon} = \int _0^\infty {g(\omega )\,\mathrm{d}\omega \over \exp (\hbar \omega /k_\mathrm{B}T)-1} \;, \end{aligned}$$

(2.37)

which can be evaluated using the substitution $x=\hbar \omega /k_\mathrm{B}T$. At low temperature, where $g(\omega )\propto \omega ^{1/2}$ in three dimensions, this yields the result

$$\begin{aligned} n_\mathrm{magnon} = \left( {k_\mathrm{B}T \over \hbar }\right) ^{3/2} \int _0^\infty {x^{1/2}\,\mathrm{d}x \over \mathrm{e}^x-1} \propto T^{3/2} \;. \end{aligned}$$

(2.38)

Since each magnon mode which is thermally excited reduces the total magnetization by one (because each magnon mode is a delocalized single reversed spin), then at low temperature the reduction in the spontaneous magnetization from the $T=0$ value is given by

$$\begin{aligned} {M(0)-M(T) \over M(0)} \propto T^{3/2} \;. \end{aligned}$$

(2.39)

This result is known as the Bloch $T^{3/2}$ law. If one repeats this calculation in two dimensions (rather than three), the integral diverges, showing that magnons spontaneously form at all non-zero temperatures, thereby destroying any magnetization. The impossibility of spontaneous magnetization in two dimensions for the Heisenberg model is known as the Mermin–Wagner  theorem [15,16,17] (see also [9]).

2.3.3 Three Spins

Let us return now to an apparently simpler system and consider three spins on the corners of an equilateral triangle. We will put the exchange interaction to be negative and thus the system is frustrated. If we put the first spin up, the next one down, then we have a dilemma of how to arrange the third one because we cannot satisfy the antiferromagnetic interactions on every bond. The solution has to be one of compromise and in fact the ground state of the classical Heisenberg model on a triangle is the so-called 120$^\circ$ state shown in Fig. 2.7a.

Fig. 2.7

The ground state of the classical Heisenberg model is the 120$^\circ$ state shown in (a), though a version with opposite chirality (b) is also possible. If each of the three spins are rotated by a constant angle [(c) and (d)] then additional ground state configurations can be obtained

In fact, there are some other possible solutions since we can choose to wind the spins round the triangle in two different ways. The configuration in Fig. 2.7b also has a 120$^\circ$ angle between adjacent spins but has the opposite chirality to that of Fig. 2.7a. Moreover, the Heisenberg model only cares about the relative angle between spins, not their absolute orientation, and therefore the configurations in Fig. 2.7c and d are also part of the ground state manifold.

Let us now solve the problem quantum mechanically. The law of addition of angular momentum now gives $\frac{1}{2}+\frac{1}{2}+\frac{1}{2} = \frac{1}{2},\frac{1}{2},\frac{3}{2}$. Now three two-dimensional representations (for three spin-$\frac{1}{2}$) have a dimensionality of $2^3=8$ which is equal to two two-dimensional representation and a four-dimensional representation (for two spin-$\frac{1}{2}$ and a single spin-$\frac{3}{2}$, so $2^3=2+2+4$). Another way of writing this combination is

$$\begin{aligned} D^{(\frac{1}{2})}\otimes D^{(\frac{1}{2})} \otimes D^{(\frac{1}{2})} = 2D^{(\frac{1}{2})}\oplus D^{(\frac{3}{2})} \;. \end{aligned}$$

(2.40)

For three spins we have that

$$\begin{aligned} \hat{\varvec{S}}^\mathrm{tot} = \hat{\varvec{S}}_1 + \hat{\varvec{S}}_2 + \hat{\varvec{S}}_3 \end{aligned}$$

(2.41)

and hence

$$\begin{aligned} (\hat{\varvec{S}}^\mathrm{tot})^2 = \hat{\varvec{S}}_1^2 + \hat{\varvec{S}}_2^2 + \hat{\varvec{S}}_3^2 + 2 \sum _{\langle i,j\rangle } \hat{\varvec{S}}_i \cdot \hat{\varvec{S}}_j \;, \end{aligned}$$

(2.42)

and so using the facts that the eigenvalue of $(\hat{\varvec{S}}^\mathrm{tot})^2$ is $S^\mathrm{tot} (S^\mathrm{tot}+1)$ and the eigenvalue of $\hat{\varvec{S}}_i^2$ is $\frac{1}{2}(\frac{1}{2}+1)=\frac{3}{4}$, we have

$$\begin{aligned} \sum _{\langle i,j \rangle } \hat{\varvec{S}}_i \cdot \hat{\varvec{S}}_j = \frac{1}{2} \left( S^\mathrm{tot} (S^\mathrm{tot}+1)- 3\times \frac{3}{4}\right) \;. \end{aligned}$$

(2.43)

We have two cases: (i) $S^\mathrm{tot}=\frac{3}{2}$ implies that $\sum _{\langle i,j\rangle } \hat{\varvec{S}}_i \cdot \hat{\varvec{S}}_j = \frac{3}{4}$; (ii) $S^\mathrm{tot}=\frac{1}{2}$ implies that $\sum _{\langle i,j\rangle } \hat{\varvec{S}}_i \cdot \hat{\varvec{S}}_j = -\frac{3}{4}$. The energy levels are drawn in Fig. 2.8 and consist of two degenerate doublets at $E=-3A/4$ ($S=\frac{1}{2}$) and a quartet at $E=3A/4$.

Fig. 2.8

The energy levels for a triangle of spins consist of two degenerate doublets and a quartet

It is interesting to consider the 8 states that make up these energy levels [18]. We can write these as follows

$$\begin{aligned} |\Psi _{M=\frac{3}{2}} \rangle= & {} \vert \!\uparrow \uparrow \uparrow \rangle \nonumber \\ |\Psi _{M=\frac{1}{2}}^{(k)} \rangle= & {} {1 \over \sqrt{3}} \sum _{j=0}^2 \mathrm{e}^{2\pi ijk/3} C_3^j \vert \!\downarrow \uparrow \uparrow \rangle \nonumber \\ |\Psi _{M=-\frac{1}{2}}^{(k)} \rangle= & {} {1 \over \sqrt{3}} \sum _{j=0}^2 \mathrm{e}^{2\pi ijk/3} C_3^j \vert \!\uparrow \downarrow \downarrow \rangle \nonumber \\ |\Psi _{M=-\frac{3}{2}} \rangle= & {} \vert \!\downarrow \downarrow \downarrow \rangle \end{aligned}$$

(2.44)

Two states are obvious. These are the ‘ferromagnetic’ configurations $\vert \!\uparrow \uparrow \uparrow \rangle$ and $\vert \!\downarrow \downarrow \downarrow \rangle$. The other six contributions have a single spin-flip with respect to these ‘ferromagnetic configurations’ and so are made up of states like $\vert \!\downarrow \uparrow \uparrow \rangle$. However, a state like $\vert \!\downarrow \uparrow \uparrow \rangle$ is not exchange symmetric or antisymmetric, so you have to make linear combinations such as $\vert \!\downarrow \uparrow \uparrow \rangle + \vert \!\uparrow \downarrow \uparrow \rangle +\vert \!\uparrow \uparrow \downarrow \rangle$. This is exactly what is achieved by the sums in (2.44) (and note that the ${1/\sqrt{3}}$ factor is simply a normalization). The operators $C_3^j$ are threefold rotations of order j, and $j,k=0,1,2$.

What is more, we can recover the chiral nature noted in the classical solutions. If we define a  chirality operator $\hat{C}_z$ given by

$$\begin{aligned} \hat{C}_z = {1 \over 4\sqrt{3}} \varvec{S}_1 \cdot ( \varvec{S}_2 \times \varvec{S}_3 ) \;, \end{aligned}$$

(2.45)

then our states are eigenstates of the chirality operator

$$\begin{aligned} \hat{C}_z |\Psi _{M=\frac{3}{2}} \rangle= & {} 0 \nonumber \\ \hat{C}_z |\Psi _{M=\frac{1}{2}}^{(0)} \rangle= & {} 0 \nonumber \\ \hat{C}_z |\Psi _{M=\frac{1}{2}}^{(1)} \rangle= & {} |\Psi _{M=\frac{1}{2}}^{(1)} \rangle \nonumber \\ \hat{C}_z |\Psi _{M=\frac{1}{2}}^{(2)} \rangle= & {} -|\Psi _{M=\frac{1}{2}}^{(2)} \rangle \;. \end{aligned}$$

(2.46)

Note that the quantum numbers $k = 0, 1, 2$, and chirality $C_z =0, \pm 1$ describe the same states [18]. The states with non-zero chirality are in the pair of doublet ground states (for $A>0$) while the excited state quartet has zero chirality.

2.4 Orbitals

2.4.1 Transition Metal Ions

The Heisenberg model only depends on the relative orientation of spins, not on their absolute orientation. It, therefore, seems to take no account of the lattice in which spins are embedded. However, spins are ‘aware’ of the lattice via the spin–orbit interaction. We now turn to consider the electronic orbitals that may be occupied in real systems. We will here particularly focus on transition metal compounds in which localized moments occur. (For metallic systems a band-like description would be more appropriate.)

Fig. 2.9

Electronic states of the d-electrons in octahedrally coordinated first-row transition metal ions in commonly found oxidation states. The d-shell contains 10 electrons and so configurations $d^0$, $d^1$, $\ldots$, $d^{10}$ are possible, indicated by the vertical lines. Depending on the oxidation state chosen (and not all possibilities are chemically available) these configurations can be achieved using different first-row transition metal ions (Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn). The oxidation state is indicated by the roman superscript, so that Cu$^\mathrm{II}$ is copper in its doubly ionized oxidation state (i.e. Cu$^{2+}$). An octahedral crystal field splits the ten d-levels into a sixfold $t_{2g}$ level and a fourfold $e_g$ level and the electron configurations are shown schematically at the bottom of the figure together with their description using the conventional spectroscopic notation (‘A’ signifies an orbitally non-degenerate state, ‘E’ doubly degenerate and ‘T’ triply degenerate). For ions with $d^4$, $d^5$, $d^6$ and $d^7$ configuration, there is the possibility of low-spin and high-spin configurations (Figure from [19])

Commonly occurring first-row transition metal ions are shown in Fig. 2.9 (taken from [19]), illustrating the range in occupancy of the 3d shell that can be obtained using transition metal ions in different oxidation states. I also show their electronic configuration for the case in which the ion experiences an octahedral crystal field (which  splits the ten d-levels into a sixfold $t_{2g}$ level and a fourfold $e_g$ level [2]). Octahedral environments are very common in a wide variety of compound. This figure also shows that some ions are very particular about their oxidation state; for energetic reasons, Sc$^\mathrm{III}$ and Zn$^\mathrm{II}$ are the only stable states. On the other hand, an ion such as Mn can have a very large range of oxidation states from Mn$^\mathrm{II}$ (in MnO) to Mn$^\mathrm{VII}$ (in potassium permanganate KMnO$_4$). In fact, with clever chemistry even Mn$^\mathrm{I}$ is possible [20]! This range of occupancy leads to different spin and orbital moments of the ion and hence can be used to control the magnetic properties of the resulting system. For ions with $d^4$, $d^5$, $d^6$ and $d^7$ configuration, there is the possibility of both low-spin and high-spin states.

2.4.2 Spin–Orbit Interaction and Crystal Fields

Now that we have the possibility of some partially filled d-levels, there can be magnetism. Next let us turn to the spin–orbit interaction which has the form

$$\begin{aligned} \lambda \hat{\varvec{S}}\cdot \hat{\varvec{L}} \;, \end{aligned}$$

(2.47)

 so that the $\hat{\varvec{S}}$ operator acts on the spin part of the wave function, while the $\hat{\varvec{L}}$ operator acts on the spatial part of the wave function. If the states are approximately atomic states, and the spin–orbit interaction acts as a perturbation, one can focus on the $\lambda S^z L^z$ part and note that

$$\begin{aligned} \hat{L}^z = -\mathrm{i}\hbar {\partial \over \partial \phi } \;, \end{aligned}$$

(2.48)

which has eigenfunctions $\mathrm{e}^{\mathrm{i}m\phi }$, i.e.

$$\begin{aligned} \hat{L}^z \mathrm{e}^{\mathrm{i}m\phi } = -\mathrm{i}\hbar {\partial \over \partial \phi }\mathrm{e}^{\mathrm{i}m\phi } = m\hbar \mathrm{e}^{\mathrm{i}m\phi } \;. \end{aligned}$$

(2.49)

Now the crystal field is a real potential which is due to electrostatic fields from neighbouring ions. The eigenfunctions of the crystal field cannot be proportional to $\mathrm{e}^{\mathrm{i}m\phi }$ because we require real solutions. (Recall the problem of particle in a box where the solutions are real and take the form $\cos kx$ or $\sin kx$, but not $\mathrm{e}^{\mathrm{i}kx}$, but of course we can make real functions by making linear combinations such as $\mathrm{e}^{\mathrm{i}kx} \pm \mathrm{e}^{-\mathrm{i}kx}$ and making a wave function out of something proportional to that.) To make a crystal field state we must, therefore, look for linear combinations of eigenfunctions such as

$$\begin{aligned} |\psi \rangle = \mathrm{e}^{\mathrm{i}m\phi }\pm \mathrm{e}^{-\mathrm{i}m\phi } \;. \end{aligned}$$

(2.50)

This kind of state though will automatically have zero angular momentum along the z-direction because it is made up of an equal contribution of a state with $\langle L^z\rangle =m\hbar$ and $\langle L^z\rangle =-m\hbar$. In fact, this idea works for all directions and

$$\begin{aligned} \langle \hat{\varvec{L}} \rangle = 0 \;. \end{aligned}$$

(2.51)

Fig. 2.10

Angular representation of a p-orbitals and b d-orbitals

For example, if $l=1$, there are three states with $m=1,0,-1$ with wave functions given by the spherical harmonics $Y_{1m}(\theta ,\phi )$, and are therefore proportional to $\sin \theta \,\mathrm{e}^{\mathrm{i}\phi }$, $\cos \theta$ and $\sin \theta \,\mathrm{e}^{-\mathrm{i}\phi }$, respectively. We could write these states as $|1\rangle$, $|0\rangle$ and $|-1\rangle$. However, these are not the famous p-orbitals familiar from chemistry books. These arise in the formation of chemical bonds due to (real) electrostatic effects and must, therefore, be linear combinations of exactly the kind we are talking about. Thus the p-orbitals that line up along the x-, y- and z-directions [see Fig. 2.10a] are the zero-angular-momentum linear combinations given below:

$$\begin{aligned} |p_x\rangle= & {} { |1\rangle + |-1\rangle \over \sqrt{2} } \nonumber \\ |p_y\rangle= & {} { |1\rangle - |-1\rangle \over \sqrt{2}\mathrm{i}} \nonumber \\ |p_z\rangle= & {} |0\rangle \;. \end{aligned}$$

(2.52)

 

What we see here is the phenomenon of quenching of angular momentum and it is interesting that it shows up even in the unfamiliar setting of the ‘balloon animals’ of p-orbitals. Of course in magnetism we are usually more interested in considering d-orbitals or f-orbitals but the same principles hold. For example, the equivalent equations for the d-orbitals [see Fig. 2.10b] are

$$\begin{aligned} |d_{xy}\rangle= & {} { |2\rangle - |-2\rangle \over \sqrt{2}\mathrm{i} } \nonumber \\ |d_{x^2-y^2}\rangle= & {} { |2\rangle + |-2\rangle \over \sqrt{2} } \nonumber \\ |d_{yz}\rangle= & {} { -|1\rangle - |-1\rangle \over \sqrt{2}\mathrm{i} } \nonumber \\ |d_{zx}\rangle= & {} { -|1\rangle + |-1\rangle \over \sqrt{2} } \nonumber \\ |d_{z^2}\rangle= & {} |0\rangle \;. \end{aligned}$$

(2.53)

2.4.3 Jahn–Teller Effect

It can sometimes be energetically favourable for, say, an octahedron to spontaneously distort as shown in Fig. 2.11 because the energy cost of increased elastic energy is balanced by a resultant electronic energy saving due to the distortion. This phenomenon is known as the Jahn–Teller effect [21]. The distortion lowers the overall energy by breaking an orbital degeneracy. For example, Mn$^{3+}$ ions (which have a configuration $3d^4$) in an octahedral environment show this kind of behaviour (see Fig. 2.11) because the distortion can break the orbital degeneracy in the $e_g$ levels. In contrast, Mn$^{4+}$ ions (3$d^3$) would not show this effect because there is no net lowering of the electronic energy by a distortion.

To describe the effect, at least at the phenomenological level, we will assume that the distortion of the system can be quantified by a parameter Q, which denotes the distance of distortion along an appropriate normal mode coordinate. This gives rise to an energy cost which is quadratic in Q and can be written as

$$\begin{aligned} E(Q) = \frac{1}{2}M\omega ^2Q^2 \;, \end{aligned}$$

(2.54)

where M and $\omega$ are, respectively, the mass of the anion and the angular frequency corresponding to the particular normal mode. Clearly the minimum distortion energy is zero and is obtained when $Q=0$ (no distortion).

Fig. 2.11

The Jahn–Teller effect for Mn$^{3+}$ ($3d^4$). An octahedral complex (left) can distort (right), thus splitting the $t_{2g}$ and $e_g$ levels. The distortion lowers the energy because the singly occupied $e_g$ level is lowered in energy. The saving in energy from the lowering of the $d_{xz}$ and $d_{yz}$ levels is exactly balanced by the raising of the $d_{xy}$ level

The distortion also raises the energy of certain orbitals while lowering the energy of others. If all orbitals are either completely full or completely empty, this does not matter since the overall energy is simply given by (2.54). However, in the cases of partially filled orbitals this effect can be highly significant since the system can have a net reduction in total energy. The electronic energy dependence on Q could be rather complicated, but one can write it as a Taylor series in Q and provided the distortion is small it is legitimate to keep only the term linear in Q. Let us, therefore, suppose that the energy of a given orbital has a term either $+AQ$ or $-AQ$ corresponding to a raising or a lowering of the electronic energy, where A is a suitable constant, assumed to be positive. Then the total energy E(Q) is given by the sum of the electronic energy and the elastic energy

$$\begin{aligned} E(Q) = \pm AQ + \frac{1}{2}M\omega ^2Q^2 \;, \end{aligned}$$

(2.55)

where the two possible choices of the sign of the AQ term give rise to two separate curves. If we consider only one of them we can find the minimum energy for that orbital using $\partial E/\partial Q=0$ which yields a value of Q given by

$$\begin{aligned} Q_0 = { A \over M\omega ^2} \end{aligned}$$

(2.56)

and a minimum energy which is given by $E_\mathrm{min} = -A^2/2M\omega ^2$ which is less than zero. If only that orbital is full, then the system can make a net energy saving by spontaneously distorting.

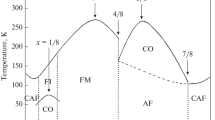
LaMnO$_3$ contains Mn in the Mn$^{3+}$ state which is a Jahn–Teller ion. LaMnO$_3$ shows A-type antiferromagnetic ordering. If a fraction x of the trivalent La$^{3+}$ ions are replaced by divalent Sr$^{2+}$, Ca$^{2+}$ or Ba$^{2+}$ ions, holes are introduced on the Mn sites. This results in a fraction $1-x$ of the Mn ions remaining as Mn$^{3+}$ ($3d^4$, $t_{2\mathrm{g}}^3$ $e_\mathrm{g}^1$) and a fraction x becoming Mn$^{4+}$ ($3d^4$, $t_{2\mathrm{g}}^3$ $e_\mathrm{g}^0$). When $x=0.2$ the Jahn–Teller distortion  vanishes and the system becomes ferromagnetic with a Curie temperature ($T_{\mathrm {C}})$ around room temperature. Above $T_\mathrm{C}$, the material is insulating and non magnetic, but below $T_\mathrm{C}$, it is metallic and ferromagnetic. Particularly near $T_\mathrm{C}$, the material shows an extremely large magnetoresistive effect which has been called colossal magnetoresistance. 

The situation is actually more complicated because the carriers interact with phonons because of the Jahn–Teller effect. The strong electron–phonon coupling in these systems implies that the carriers are actually polarons above $T_\mathrm{C}$, i.e. electrons accompanied by a large lattice distortion. These polarons are magnetic and are self-trapped in the lattice. The transition to the magnetic state can be regarded as an unbinding of the trapped polarons. There are other signatures of the electron–phonon couplings, including magnetic-field dependent structural transitions and charge ordering.

2.5 Conclusion

This chapter has discussed a number of important concepts in magnetism. Clearly this has just scratched the surface and for more details the reader should look elsewhere [2,3,4,5]. Nevertheless, these principles are helpful in understanding the wide variety of magnetic materials that are being studied, from frustrated magnets [22] to molecular magnets [19, 23] and from permanent magnetic materials [24] to spintronics [25].