Abstract
We introduce implicit morphisms as a concept in formal systems based on theories and theory morphisms. The idea is that there may be at most one implicit morphism from a theory S to a theory T, and if S-expressions are used in T their semantics is obtained by automatically inserting the implicit morphism. The practical appeal of implicit morphisms is that they hit the sweet-spot of being extremely simple to understand and implement while significantly hel** with structuring large collections of theories.
Concrete applications include elegantly identifying isomorphic theories and extending theories with definitions and theorems as well as efficiently building and maintaining large, fine-granular, and heterogeneous hierarchies of theories. Our results are formulated and implemented in the  language and system, and we expect they can be transferred to other morphism-based formalisms relatively easily.
language and system, and we expect they can be transferred to other morphism-based formalisms relatively easily.
F. Rabe—The author was supported by DFG grant RA-18723-1 OAF and EU grant Horizon 2020 ERI 676541 OpenDreamKit.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Motivation. Theory morphisms have proved an essential tool for managing collections of theories in logics and related formal systems. They can be used to structure theories and build large theories modularly from small components or to relate different theories to each other [SW83, AHMS99, FGT92]. Areas in which tools based on theories and theory morphisms have been developed include specification [GWM+93, MML07], rewriting [CELM96], theorem proving [FGT93, KWP99], and knowledge representation [RK13]. Closely related concepts are used in both object-oriented (classes) and functional (type classes) programming languages.
These systems usually use a logic L for the low-level formalization of domain knowledge, and a diagram D in the category of L-theories and L-morphisms for the high-level structure of large bodies of knowledge.
For example, a document might reference an existing theory \({\mathtt {Monoid}}\), define a new theory \({\mathtt {Group}}\) that extends \({\mathtt {Monoid}}\), define a theory \({\mathtt {DivGroup}}\) (providing an alternative formulation of groups based on the division operation), and then define two theory morphisms  that witness an isomorphism between these theories. This would result in the diagram below.Footnote 1
that witness an isomorphism between these theories. This would result in the diagram below.Footnote 1

The key idea behind implicit morphisms is very simple: We maintain an additional diagram I, which is a commutative subdiagram of D and whose morphisms we call implicit. The condition of commutativity guarantees that I has at most one morphism i from theory S to theory T, in which case we write  . Commutativity makes the following language extension well-defined: if
. Commutativity makes the following language extension well-defined: if  , then any identifier c that is visible to S may also be used in T-expressions, with the semantics being that c abbreviates i(c). For example, in the diagram above, we may choose to label \({\mathtt {DG2G}}\) implicit. Immediately, every abbreviation or theorem that we have formulated in the theory \({\mathtt {DivGroup}}\) becomes available for use in \({\mathtt {Group}}\) without any syntactic overhead. We can even label \({\mathtt {G2DG}}\) implicit as well if we prove the isomorphism property to ensure that I remains commutative, thus capturing the mathematical intuition that \({\mathtt {Group}}\) and \({\mathtt {DivGroup}}\) are just different formalizations of the same concept. While these morphisms must be labeled manually, any inclusion morphism like the one from \({\mathtt {Monoid}}\) to \({\mathtt {Group}}\) can be made implicit automatically.
, then any identifier c that is visible to S may also be used in T-expressions, with the semantics being that c abbreviates i(c). For example, in the diagram above, we may choose to label \({\mathtt {DG2G}}\) implicit. Immediately, every abbreviation or theorem that we have formulated in the theory \({\mathtt {DivGroup}}\) becomes available for use in \({\mathtt {Group}}\) without any syntactic overhead. We can even label \({\mathtt {G2DG}}\) implicit as well if we prove the isomorphism property to ensure that I remains commutative, thus capturing the mathematical intuition that \({\mathtt {Group}}\) and \({\mathtt {DivGroup}}\) are just different formalizations of the same concept. While these morphisms must be labeled manually, any inclusion morphism like the one from \({\mathtt {Monoid}}\) to \({\mathtt {Group}}\) can be made implicit automatically.
Contribution. At the highest level, our contribution is the observation that implicit morphisms form a sweet spot of a very simple language feature that has substantial practical uses. We recommend using implicit morphisms in all theory morphism–based formalisms. More concretely, we present a formal system for develo** structured theories with implicit morphisms based on the  language [RK13]. We choose
language [RK13]. We choose  because it provides a simple framework for working with theories and morphisms while remaining logic-independent:
because it provides a simple framework for working with theories and morphisms while remaining logic-independent:  allows embedding a large variety of declarative languages L (logics, type-theories, etc.) so that our results immediately yield an implementation of implicit morphisms for any such L. We also expect but do not describe here that other morphism-based systems can be easily extended to allow for implicit morphisms.
allows embedding a large variety of declarative languages L (logics, type-theories, etc.) so that our results immediately yield an implementation of implicit morphisms for any such L. We also expect but do not describe here that other morphism-based systems can be easily extended to allow for implicit morphisms.
We describe several example applications of implicit morphisms in detail: the identification of isomorphic theories, definitional extensions of theories, building large hierarchies of theories with many rarely used intermediate theories, seamlessly moving theories across logic morphisms, and transparently refactoring theory hierarchies.
Previous Work. Implicit morphism were first conceived by Rabe in 2010 and implemented as part of the Twelf system [PS99] (which implements the dependent type theory LF). The theory behind this implementation was never written up and not published. But the implementation already scaled well, and implicit morphisms were used in the LATIN logic atlas [CHK+11] built by Rabe and others in 2009–2012. The LATIN atlas already has around a 1000 theories and atomic morphisms, and about 50 of the latter are marked as implicit. It also has a few hundred inclusions, each of which induces another implicit morphism.
Since then, MMT has been developed, and
-
implicit morphisms were generalized from LF to the logic-independent level of MMT,
-
their theory was worked out,
-
they were reimplemented from scratch as a part of MMT.
MMT is backwards-compatible with Twelf, and the LATIN atlas including its implicit morphisms can be used from within MMT. The present paper introduces these results in their final, most elegant form.
Overview. In Sect. 2, we present the syntax and semantics of  . Even though the
. Even though the  language is not new, our presentation is an entirely novel contribution in itself: it is much simpler and more elegant than the original one in [RK13]. Crucially, this increase in simplicity allows spelling out the syntax and semantics of implicit morphisms, which we do in Sect. 3, within a few pages. In Sect. 4, we present applications. Finally we discuss related and future work in Sect. 5.
language is not new, our presentation is an entirely novel contribution in itself: it is much simpler and more elegant than the original one in [RK13]. Crucially, this increase in simplicity allows spelling out the syntax and semantics of implicit morphisms, which we do in Sect. 3, within a few pages. In Sect. 4, we present applications. Finally we discuss related and future work in Sect. 5.
2 Theories and Theory Morphisms
2.1 Overview
Flat Modules. Flat theories are lists of constant declarations \(c:E[=e]\) where E and e are expressions, and the latter is optional. We write \(\mathtt {dom}(T)\) for the set of constant identifiers c in T. Every theory induces the set \(\mathtt {Obj}(T)\) for the set of closed expressions using only the symbols \(c\in \mathtt {dom}(T)\). Constant declarations subsume virtually all basic declarations common in formal systems such as type/function/predicate symbols, axioms, theorems, inference rules, etc. In particular, theorems can be represented via the propositions-as-types correspondence as declarations \(c:F=P\), which establish theorem F via proof P. Similarly,  expressions subsume virtually all objects common in formal systems such as terms, types, formulas, proofs.
expressions subsume virtually all objects common in formal systems such as terms, types, formulas, proofs.
Flat morphisms from a theory S to a theory T are lists of assignments \(c:=e\) where \(c\in \mathtt {dom}(S)\) and \(e\in \mathtt {Obj}(T)\). Every morphism M induces a homomorphic extension \(M(-):\mathtt {Obj}(S)\rightarrow \mathtt {Obj}(T)\), which replaces every \(c\in \mathtt {dom}(S)\) in an S-expression with the T-expression e such that \(c:=e\) in M.
A diagram consists of a set of theory and morphism declarations. For a given diagram, we write \(\mathtt {Thy}\) for the set of declared theories. For theories \(S,T\in \mathtt {Thy}\), we write \(\mathtt {Mor}(S,T)\) for the set of morphisms defined by
-
for every declaration \(m:S\rightarrow T=\{\cdot \}\), we have \(m\in \mathtt {Mor}(S,T)\),
-
for every \(T\in \mathtt {Thy}\), we have \( id _{T}\in \mathtt {Mor}(T,T)\),
-
for every \(M\in \mathtt {Mor}(R,S)\) and \(N\in \mathtt {Mor}(S,T)\), we have \(M;N\in \mathtt {Mor}(R,T)\) (where M; N corresponds to the usual function composition).
\(\mathtt {Thy}\) and \(\mathtt {Mor}(S,T)\) form the category of theories and morphisms.
The theories and morphisms in a diagram may be structured (e.g., by using include declarations), and  defines their semantics via flattening, which defines for each \(T\in \mathtt {Thy}\) the flat theory \(T^\flat \), and for each \(M\in \mathtt {Mor}(S,T)\) the flat morphism \(M^\flat \) from \(S^\flat \) to \(T^\flat \).
defines their semantics via flattening, which defines for each \(T\in \mathtt {Thy}\) the flat theory \(T^\flat \), and for each \(M\in \mathtt {Mor}(S,T)\) the flat morphism \(M^\flat \) from \(S^\flat \) to \(T^\flat \).
Logics and Well-Formed Expressions. The logic and the definition of well-formed expressions are not a primary interest of this paper, and we only recap the essential structure needed in the sequel. We refer to [Rab17] for details.
 is independent of the base logic and provides a theory and theory morphism layer on top of an arbitrary declarative language. Individual logics L arise as fragments of
is independent of the base logic and provides a theory and theory morphism layer on top of an arbitrary declarative language. Individual logics L arise as fragments of  : they single out the well-formed expressions by defining the judgment \(\vdash _T e=e':E\) for ty** and equality. (We treat the plain ty** judgment \(\vdash _T e:E\) as the special case \(\vdash _T e=e:E\).) The logic L is itself represented as an
: they single out the well-formed expressions by defining the judgment \(\vdash _T e=e':E\) for ty** and equality. (We treat the plain ty** judgment \(\vdash _T e:E\) as the special case \(\vdash _T e=e:E\).) The logic L is itself represented as an  theory, which we call the meta-theory of T. L provides, in particular, the primitive operators and ty** rules that are used to form the well-formed expressions of T. L may and often has a meta-theory as well, usually a logical framework used to define the logic. Unless mentioned otherwise, all results in this paper apply for a fixed arbitrary meta-theory, which we will occasionally omit from the notation.
theory, which we call the meta-theory of T. L provides, in particular, the primitive operators and ty** rules that are used to form the well-formed expressions of T. L may and often has a meta-theory as well, usually a logical framework used to define the logic. Unless mentioned otherwise, all results in this paper apply for a fixed arbitrary meta-theory, which we will occasionally omit from the notation.
The declarations in theories and assignments in morphisms are subject to ty** conditions, and the main theorem about  is that under reasonable assumptions on L, the well-typed morphisms \(M:S\rightarrow T\) preserve all judgments, i.e., if \(\vdash _S e=e':E\), then \(\vdash _T M(e)=M(e'):M(E)\). This includes the preservation of truth via the propositions-as-types principle if E is a proposition and e its proof.
is that under reasonable assumptions on L, the well-typed morphisms \(M:S\rightarrow T\) preserve all judgments, i.e., if \(\vdash _S e=e':E\), then \(\vdash _T M(e)=M(e'):M(E)\). This includes the preservation of truth via the propositions-as-types principle if E is a proposition and e its proof.
We do not give all rules for these judgments. The only rule that is relevant to our purposes here is the one for constants:
(Here, we merge the two cases where c has a/no definiens e into one rule for convenience.) Correspondingly, the definition of the homomorphic extension of a morphism with domain S includes the following case for constants:
Here if c has a definiens in S, we expand it before applying M.Footnote 2
These base cases introduce a mutual recursion between well-formedness and flattening: the well-formedness of a declaration in a theory depends on the flattening of all preceding declarations; correspondingly, the well-formedness of an assignment in a morphism depends on the homomorphic extension of the morphism obtained by flattening of all preceding assignments. Vice versa, well-formedness is a precondition for defining the flattening—the definition of flattening may become nonsensical if applied to ill-formed modules. It might be desirable to define well-formedness independently of flattening. But our definition captures the typical behavior of practical systems, which first parse, check, and flatten one declaration entirely before moving on to the next one.
Therefore, we will make flattening a partial function, i.e., \(X^\flat \) is undefined if the module X is not well-formed.
2.2 Syntax
We start with the syntax for theories (which arises as a special case of the one given in [RK13]):
Definition 1
(Theory). The grammar for theories and expressions is

In a theory declaration \(T:L=\{\vec {D}\}\), the meta-theory L (if present) must be a previously declared theory, each symbol name n may be declared only once, and its type and definiens (if present) must be closed expressions over the previously introduced constants (including those of L). We omit the productions and ty** rules for the remaining expressions, which include application, binding, variables, literals, etc.
Example 1
For the purposes of our running examples, we assume a fixed meta-theory  that provides a simple type system: type is the universe of types,
that provides a simple type system: type is the universe of types,
 is the type of functions, and lambda abstraction is written
is the type of functions, and lambda abstraction is written
 . We also use
. We also use  notations, which are attached to constant declarations as
notations, which are attached to constant declarations as
 these are omitted from the formal grammar above because we only use them in the examples.
these are omitted from the formal grammar above because we only use them in the examples.
Then the (flat) theories \({\mathtt {Group}}\) and \({\mathtt {DivGroup}}\) from the introduction are:

We proceed accordingly for flat morphisms:
Definition 2
(Morphism). The grammar for morphisms is

A morphism \(m:S\rightarrow T=^M\{\vec {A}\}\) must contain exactly one assignment \(c:=e\) for each \((c:E)\in S^\flat \), all of which must satisfy \(\vdash _T e: m(E)\). Moreover, if S has a meta-theory L, then M must be present and must be a morphism from L to T.
Example 2
(Morphisms). We give the morphism \({\mathtt {DG2G}}\) between the theories from Example 3:

Here  maps the meta-theory to itself. Then universe and unit of a division group are mapped to the corresponding notions of a group. And we have \({\mathtt {DG2G}}(a/b)=a\circ b^{-1}\). Additionally, the morphism maps every axiom of \({\mathtt {DivGroup}}\) to a proof in \({\mathtt {Group}}\) of the translated statement, but we omit those assignments.
maps the meta-theory to itself. Then universe and unit of a division group are mapped to the corresponding notions of a group. And we have \({\mathtt {DG2G}}(a/b)=a\circ b^{-1}\). Additionally, the morphism maps every axiom of \({\mathtt {DivGroup}}\) to a proof in \({\mathtt {Group}}\) of the translated statement, but we omit those assignments.
Finally, we define diagrams as collections of modules:
Definition 3
(Diagram). A diagram is a list of theory and morphism declarations:

Each theory/morphism declaration must have a unique name and be well-formed relative to the diagram preceding it.
At this point, the grammar only allows forming flat theories and morphisms. Structuring features can be added to the language incrementally and individually.
Example 3
(Includes). We extend the grammar with

This allows writing the theory \({\mathtt {Group}}\) from Example 1 by extending a theory of monoids. Again omitting all axioms, this looks as follows:

2.3 Semantics
Flattening. The definition of flattening is compositional in the sense that new modularity principles can be added independently of each other.
Definition 4
(Flattening). For the base case, of a theory \(t:L=\{\varSigma \}\), we define \(t^\flat \) by induction on the declarations in \(\varSigma \):
where \(\cdot \) denotes the empty sequence. If L is not present, we can assume it to be the empty theory.
Here \(D^{\flat }\) is the flattening of declaration D relative to \(\varSigma ^\flat \). At this point, we only have one case for declarations D, namely constant declarations. Their flattening is trivial:
where t is the name of the containing theory.
Correspondingly, for a declared morphism \(m:S\rightarrow T=^{[M]}\{\sigma \}\), \(m^\flat \) is defined by induction on the assignments in \(\sigma \):
with the trivial base case
If M is not present, we can assume it to be empty morphism.
Moreover, for \(T\in \mathtt {Thy}\) we define \( id _{T}^\flat =\{c:=c \;|\; (c:E)\in T^\flat \}\) And for \(M;N\in \mathtt {Mor}(R,T)\), we define \((M;N)^\flat =\{c:=N^\flat (M^\flat (c)) \;|\; (c:E)\in R^\flat \}\). Note that in both cases, we only have to consider constants without definiens.
Example 4
(Includes (continued from Example 3)). The \({\mathbf {include}}\) operator adds new declarations D to a theory, so we have to add cases to the definition of \(D^{\flat }\). We do this as follows
This has the effect of copying over all declarations from the included into the including theory.
There is some flexibility as to when the including and the included theory have different meta-theories L resp. \(L'\). We define that such an include is only allowed if \(L'\) is also included into L. That way, an include declaration never changes the meta-theory of the including theory.
Note that, because \(S^\flat \) is a set of declarations, the include relation is transitive: if t includes s via two different paths, \(t^\flat \) only contains one copy of the declarations of \(s^\flat \).
Because we use qualified identifiers t?n, includes can never lead to name clashes. The situation is slightly more complicated for morphisms: if a morphism \(\sigma \) out of t includes two different morphisms out of s, these have to agree. Therefore, flattening is not always defined:
if \(\sigma ,{\mathbf {include}}{\;M}\) is well-formed and \(M^\flat \) agrees with \(\sigma ^\flat \) on any constant that is in the domain of both.
Example 5
(Continuing Example 3). \({\mathtt {Group}}^\flat \) is obtained by copying all included symbols (from \({\mathtt {Monoid}}\)) over to \({\mathtt {Group}}\), resulting in the theory as given in Example 1 except that the identifiers are now, e.g., \({\mathtt {Monoid}}?U\) instead of \({\mathtt {Group}}?U\).
Remark 1
(Qualified Identifiers). According to the grammar, any occurrence of a constant c in an expression is of the form t?n, i.e., qualified by its theory name. In the definition all declarations in \(t^\flat \) are qualified accordingly. This precludes any name clashes when constants of the same local name are declared in multiple theories that become part of \(t^\flat \), e.g., via the meta-theory or includes.
The form t?n is abstract system-facing syntax. In concrete user-facing syntax (as used in our examples), it is usually sufficient to write n and let the  parser infer which constant is meant.
parser infer which constant is meant.
3 Implicit Morphisms
3.1 Overview
Our key idea is to use a commutative subdiagram of the  diagram, which we call the implicit diagram. It contains all theories but only some of the morphisms—the ones designated as implicit. Because the implicit-diagram commutes, there can be at most one implicit morphism from S to T—if this morphism is i, we write
diagram, which we call the implicit diagram. It contains all theories but only some of the morphisms—the ones designated as implicit. Because the implicit-diagram commutes, there can be at most one implicit morphism from S to T—if this morphism is i, we write  . The implicit-diagram generalizes the inclusion relation: All identity and inclusion morphisms are implicit, and we recover the inclusion relation
. The implicit-diagram generalizes the inclusion relation: All identity and inclusion morphisms are implicit, and we recover the inclusion relation  as the special case
as the special case  . And just like inclusion, the relation “exists i such that
. And just like inclusion, the relation “exists i such that  ” is a preorder.
” is a preorder.
Consequently, many of the advantages of inclusions carry over to implicit morphisms:
-
It is very easy to maintain the implicit-diagram, e.g., as a partial map that assigns to a pair of theories the implicit morphism between them (if any).
-
We can generalize the visibility of identifiers: If
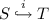 , we can use all S-identifiers in T as if S were included into T. Any \(c\in \mathtt {dom}(S)\) is treated as a valid T-identifiers with definiens M(c).
, we can use all S-identifiers in T as if S were included into T. Any \(c\in \mathtt {dom}(S)\) is treated as a valid T-identifiers with definiens M(c). -
We can use canonical identifiers S?n without worrying about ambiguity.
Because there can be at most one implicit morphism
 , using S?n as an identifier in T is unambiguous.
, using S?n as an identifier in T is unambiguous.
In practice, the  system searches for an implicit morphism
system searches for an implicit morphism  whenever needed to make an expression well-formed, e.g.,
whenever needed to make an expression well-formed, e.g.,
-
An S-constant c is used in T: treat c as an abbreviation for i(c).
-
A model M of T is used even though a model of S is expected: reduce M via i.
-
A morphism \(M:R\rightarrow S\) is composed with a morphism \(M':T\rightarrow U\): treat \(M;M'\) like \(M;i;M'\).
3.2 Syntax
We introduce the family of sets \(\mathtt {Mor^i}(S,T)\) as a subset of \(\mathtt {Mor}(S,T)\), holding the implicit morphisms. The intuition is that \(\mathtt {Thy}\) and \(\mathtt {Mor^i}(S,T)\) (up to equality of morphisms) form a thin broad subcategory of \(\mathtt {Thy}\) and \(\mathtt {Mor}(S,T)\).
It remains to define which morphisms are implicit. For that purpose, we allow  declarations to carry attributes:
declarations to carry attributes:
Definition 5
(Attributes for Implicitness). We add the following productions

The set of attributes is itself extensible, and the above grammar only lists the one that we use to get started. Additional attributes can be added when adding modularity principles.
Example 6
We can now change the declaration of the morphism \({\mathtt {DG2G}}\) from Example 2 by adding the attribute \({\mathbf {implicit}}\).
3.3 Semantics
We only have to make two minor changes to the semantics to accommodate implicit morphisms. The first change governs how we obtain implicit morphisms, the second one how we use them.
Definition 6
(Obtaining Implicit Morphisms). We define the set \(\mathtt {Mor^i}(S,T)\subseteq \mathtt {Mor}(S,T)\) of implicit morphisms to contain the following elements:
-
all declared morphisms \(m:S\rightarrow T=\{\sigma \}\) whose declaration carries the attribute \({\mathbf {implicit}}\),
-
if t has meta-theory L, the identity map as an implicit morphism \(L\rightarrow t\),
-
all identity morphisms \( id _{T}\),
-
all compositions M; N of implicit morphisms M and N,
-
all morphisms that additional language features designate as implicit based on the use of additional attributes.
Adding an \({\mathbf {implicit}}\) attribute to a declaration is well-formed only if there is (up to equality of morphisms) at most one implicit morphism for any pair of theories.
Example 7
(Includes (continued from Example 4)). For include morphisms, we add the following definition: if a theory T contains the declaration \({\mathbf {include}}{\;S}\), then the induced morphism from S to T is implicit.
Combined with composition morphisms, we see that all transitive includes between theories are implicit. That corresponds to the intuition that anything that is included is available by its original (i.e. qualified) name.
Example 8
For our morphism \({\mathtt {DG2G}}\) from Example 6, this means that all symbols declared in the theory \({\mathtt {DivGroup}}\) (see Example 1) are now visible in the theory \({\mathtt {Group}}\) with the definitions provided by \({\mathtt {DG2G}}\). For example, we can write a/b in \({\mathtt {Group}}\), where / refers to the identifier \({\mathtt {DivGroup}}?{\mathtt {div}}\).
(Note that notations are carried over by implicit morphisms as well)
The intuition behind implicit morphisms is that all S-constants c : E that can be mapped into the current theory via an implicit morphism \(M:S\rightarrow T\) are directly available in T. We can practically realize this by adding new defined constants \(c:M(E)=M(c)\) to T. However, physically adding definitions can be inefficient. It is more elegant to modify the ty** rules such that \(\vdash _T c:M(c)=M(E)\) holds without any changes to T.
To do that, we only have to make a small modification to the original rules of  as presented in Sect. 2. To illustrate how simple the modification is, the following definition repeat the original rule first for comparison:
as presented in Sect. 2. To illustrate how simple the modification is, the following definition repeat the original rule first for comparison:
Definition 7
(Using Implicit Morphisms). We replace the rule

Note that the modified rule gives every constant a definiens. This is a technical trick to subsume the original rule: if c is already declared in T, we use \(M= id _{T}\) and obtain \(\vdash _T c=c:E\).
The following theorem is our central theoretical result. It shows that the modification made in Definition 7 has the intended properties:
Theorem 1
(Conservativity of Implicit Morphisms). For well-formed diagrams and \(S,T\in \mathtt {Thy}\) and \(M\in \mathtt {Mor^i}(S,T)\):
-
1.
Whenever the original system proves \(\vdash _T e=e':E\), so does the modified one.
-
2.
Whenever the modified system proves \(\vdash _T e=e':E\), then the original system proves \(\vdash _T \overline{e}=\overline{e'}:\overline{E}\).
Here \(\overline{E}\) is the expression that arises from E by recursively replacing every constant with its definiens.
Proof
For the first claim, we proceed by induction on derivations. We only need to consider the case where the original rule was applied. So assume it yields \(\vdash _T c[=e]:E\), i.e., \((c:E[=e]) \;\mathrm {in}\;T^\flat \). We apply the modified rule for the special case  . The conclusion reduces to
. The conclusion reduces to
-
if e is absent: \(\vdash _T c=c:E\), which is equivalent to \(\vdash _T c:E\),
-
if e is present: \(\vdash _T c=e:E\) because \(M(c)=M(e)\) according to the definition of \(M(-)\).
For the second claim, we proceed by induction on derivations. We only need to consider the case where the modified rule was applied. So assume it yields \(\vdash _T c=M(c):M(E)\) for \((c:E[=e]) \;\mathrm {in}\;S^\flat \) and  . We distinguish two cases:
. We distinguish two cases:
-
\(M(c)=c\), i.e., e is absent, and \(\overline{c}=c\). According to the definition of \(S^\flat \), this is only possible if
 (including the special case \(S=T\)). In that case, \(S^\flat \subseteq T^\flat \) and M is the include/identity morphism that maps all S-constants to themselves. Now applying the induction hypothesis to the well-formedness derivation of E yields \(\vdash _T c:\overline{E}\) as needed.
(including the special case \(S=T\)). In that case, \(S^\flat \subseteq T^\flat \) and M is the include/identity morphism that maps all S-constants to themselves. Now applying the induction hypothesis to the well-formedness derivation of E yields \(\vdash _T c:\overline{E}\) as needed. -
\(M(c)\ne c\), i.e., e is present or M assigns a non-trivial value to c. Definition expansion eliminates c in favor of M(c), and thus \(\overline{c}=\overline{M(c)}\). We only have to show that \(\vdash _T \overline{M(c)}:\overline{M(E)}\). That follows from the judgment preservation of morphisms.
With implicit morphisms, we can also relax the semantics of many structuring features:
Example 9
(Includes and Meta-Theories (continued from Example 4)). Consider \(t:L=\{\ldots ,{\mathbf {include}}{\;S},\ldots \}\) where S has meta-theory \(L'\). Instead of requiring  as in Example 4, we require only
as in Example 4, we require only  .
.
In that case, we treat \({\mathbf {include}}{\;S}\) as an abbreviation for \({\mathbf {include}}{\;i(S)}\), where i(S) is the pushout of S along i (see [Rab17] for details on  pushouts). If
pushouts). If  , this reduces to the original semantics.
, this reduces to the original semantics.
4 Applications
4.1 Identifying Theories via Implicit Isomorphisms
A common need in develo** large libraries (both in formal and informal developments) is to identify two theories S and T via a canonical choice of isomorphisms. In these cases, it is often desirable to use S-syntax and T-syntax interchangeably. But one of the major short-comings of formal theories over traditional informal developments is that formal systems usually need to spell out these isomorphisms everywhere. In this section, we show that implicit morphisms elegantly allow exactly that kind of intuitive identification: we mark the canonical isomorphisms as implicit.
In the sequel, we present several ways to obtain implicit isomorphisms conveniently. In general, note that because identity morphisms are implicit, our uniqueness requirement for implicit morphisms implies that two theories S and T must be isomorphic if there are implicit morphisms in both directions. Moreover, making a pair of isomorphisms implicit is only allowed if there are no other implicit morphisms between S and T yet.
Renamings. We say that a named morphism \(r:S\rightarrow T=\{\ldots \}\) is a renaming if
-
all assignments in its body are of the form \(c:=c'\) for T-constants \(c'\) without definiens
-
every T-constant \(c'\) without definiens occurs in exactly one assignment.
Clearly, every renaming is an isomorphism. The inverse morphisms contains the flipped assignments \(c':=c\).
We make the following extension to syntax and semantics:
-
A morphism declaration \(r:s\rightarrow t=\{\ldots \}\) may carry the attribute \({\mathbf {renaming}}\).
-
This is allowed if there are no implicit morphisms between s and t yet.
-
In that case, we define \(r\in \mathtt {Mor^i}(s,t)\) and \(r^{-1}\in \mathtt {Mor}(t,s)\).
Example 10
(Renaming). Consider a variation of the theory \({\mathtt {Monoid}}\) from Example 3 in a different library:

This theory is isomorphic to the previously introduced theory \({\mathtt {Monoid}}\) under the trivial renaming

Definitional Extensions. We say that the named theory T is a definitional extension of S if \(T=S\) or the body of T contains only
-
constant declarations with definiens, and
-
include declarations of theories that are definitional extensions of S.
If T is a definitional extension of S, it is easy to prove that T and S are isomorphic: both isomorphisms map all constants without definiens to themselves. In particular, the isomorphism \(T\rightarrow S\) maps S-constants to themselves and expands the definiens of all other constants.
We make the following extension to syntax and semantics:
-
An include declaration \({\mathbf {include}}{\;S}\) of a named theory S inside a theory T may carry the attribute \({\mathbf {definitional}}\).
-
In that case, we define \( id _{S}\in \mathtt {Mor^i}(T,S)\) (in addition to the implicit morphism \( id _{T}\in \mathtt {Mor^i}(S,T)\) that is induced by the inclusion).
Example 11
(Extension with a Theorem). We extend the theory \({\mathtt {Group}}\) from Example 3 with a theorem

Remark 2
(Conservative Extensions). A definitional extension is a special case of a conservative extension. More generally, all retractable extensions are conservative, i.e., all extensions  such that there is a morphism \(r:T\rightarrow S\) that is the identity on S. But we cannot make the retractions implicit morphisms in general because they are not necessarily isomorphisms.
such that there is a morphism \(r:T\rightarrow S\) that is the identity on S. But we cannot make the retractions implicit morphisms in general because they are not necessarily isomorphisms.
Canonical Isomorphisms. If we have isomorphisms \(m:S\rightarrow T\) and \(n:T\rightarrow S\), we simply spell them out in morphism declarations and add the keyword \({\mathbf {implicit}}\) to both. This requires no language extensions.
Example 12
Having declared the morphism \({\mathtt {DG2G}}\) (as in Example 2) implicit, we do the same with the reverse morphism \({\mathtt {G2DG}}\):

While making one of these isomorphisms implicit is straightforward, doing it for both requires checking that m and n are actually isomorphisms. Otherwise, the uniqueness condition would be violated. Thus, we have to check \(m;n= id _{s}\) and \(n;m= id _{t}\). In general, the equality of two morphisms \(f,g:A\rightarrow B\) is equivalent to \(\vdash _B f(c)=g(c)\) for all \((c:E)\in A^\flat \). Thus, if equality of expressions is decidable in the logic that  is instantiated with, then
is instantiated with, then  can check this directly.
can check this directly.
However, this does not work in practice. Already elementary examples require stronger, undecidable equality relations:
Example 13
Consider the isomorphism from Example 12. The result of map** \(x\circ y\) from \({\mathtt {Group}}\) to \({\mathtt {DivGroup}}\) and back is \(x\circ ({\mathtt {unit}}\circ y^{-1})^{-1}\). Clearly, the group axioms imply that this is equal to \(x\circ y\). But formally, that requires working with the undecidable equality of first-order logic.
Therefore, in our running example, we can only make one of the two isomorphisms implicit at this point.
In the sequel, we design a general solution to this problem. It allows systematically proving the equality of two morphisms and using that to make both isomorphisms implicit. This is novel work that requires significant prerequisites and is only peripherally related to implicit morphisms. Therefore, we only sketch the idea and leave the details to future work.
We add a language feature to  to prove equalities between morphisms: We add the productions
to prove equalities between morphisms: We add the productions

We define the declaration \({\mathbf {equal}}\, M=N:S\rightarrow T \,{\mathbf {by}} \{\sigma \}\) to be well-formed iff
-
\(M:S\rightarrow T\) and \(N:S\rightarrow T\) are well-formed morphisms
-
\(\sigma \) contains exactly one assignment \(c:=p\) for every \((c:E)\in S^\flat \)
-
for each of these assignments \(c:=p\), the term p is a proof of \(\vdash _T M(c)=N(c)\).
Example 14
(Isomorphisms). With the above extension in place, we can make both isomorphisms m and n from above implicit:
where the isomorphisms are as above and we omit all the equality proofs.
There is a subtle difficulty in marking \({\mathtt {G2DG}}\) as \({\mathbf {implicit}}\): the implicit-diagram only commutes after proving the equalities, which are only declared later. One option is to delay the commutativity check until the equalities have been checked. In that case, care must be taken to avoid using the implicitness of \({\mathtt {G2DG}}\) while proving the equalities. But we obtain a more elegant solution from the observation that it is always sound and harmless to automatically make the inverse of an implicit isomorphism implicit as well. Thus, we can omit the attribute \({\mathbf {implicit}}\) on \({\mathtt {G2DG}}\) altogether and use an implementation that infers that \({\mathtt {G2DG}}\) is the inverse of an implicit isomorphism.
4.2 Fine-Granular and Flexible Theory Hierarchies
A common problem when defining modular theory hierarchies is that the most natural include-hierarchy for the most important theories is not necessarily the same as the most comprehensive hierarchy. For example, Example 3 defines \({\mathtt {Group}}\) with an include from \({\mathtt {Monoid}}\). Instead, we could have used an intermediate theory and includes  .
.
It is very common to have increasingly strong theories R, S, T, where a design with two includes  is not desirable:
is not desirable:
-
Often
 has been defined first and S only later. This is very common because people usually formalize the most important theories (e.g., \({\mathtt {Monoid}}\) and \({\mathtt {Group}}\)) first. But inserting S is not easy in retrospect—changing the theory hierarchy (which is one of the most fundamental structures of a library) usually presents a very expensive refactoring problem. And even if we systematically use includes for every known intermediate theory like S (as done in [CFO11]), we might later discover a new intermediate theory that should have been added.
has been defined first and S only later. This is very common because people usually formalize the most important theories (e.g., \({\mathtt {Monoid}}\) and \({\mathtt {Group}}\)) first. But inserting S is not easy in retrospect—changing the theory hierarchy (which is one of the most fundamental structures of a library) usually presents a very expensive refactoring problem. And even if we systematically use includes for every known intermediate theory like S (as done in [CFO11]), we might later discover a new intermediate theory that should have been added. -
Often the most natural axioms to use in T are the same independent of whether T includes R or S (e.g., users might prefer the usual inverse-element axioms in \({\mathtt {Group}}\) even if they have included \({\mathtt {CancellationMonoid}}\)). In that case, the axioms of S become provable in T if we use
 . This either causes T to have redundant axioms or requires a more complex include mechanism that allows T to include S in a way that turns some of S-axioms into theorems.
. This either causes T to have redundant axioms or requires a more complex include mechanism that allows T to include S in a way that turns some of S-axioms into theorems.
Therefore, it is common to use a commuting triangle consisting of two includes  and
and  and one morphism \(m:S\rightarrow T\). But this is awkward because the relation “every T is an S” is now mediated by m rather than being canonical. Implicit morphisms provide a simple solution to this problem: we keep the triangle but make the morphism m implicit. This captures exactly the canonical conversion from S to T.
and one morphism \(m:S\rightarrow T\). But this is awkward because the relation “every T is an S” is now mediated by m rather than being canonical. Implicit morphisms provide a simple solution to this problem: we keep the triangle but make the morphism m implicit. This captures exactly the canonical conversion from S to T.
Already the elementary algebraic hierarchy provides countless examples of such situations. For a small fragment of the hierarchy of magmas, Fig. 1 shows one possible design using numerous implicit morphisms. In particular, it uses some of the examples and features from this paper, e.g., an implicit isomorphism to identify the order-theoretic and the algebraic development of semilattices.
It also uses multiple implicit morphisms to introduce the various intermediate theories between  . All of these are of the form \(t=\{{\mathbf {include}}{\;{\mathtt {Band}}},\,a: F\}\), e.g., \({\mathtt {LeftRegularBand}}\) uses \(F=\forall x,z. z\circ x\circ z \doteq z\circ x\). The implicit morphisms map the constants from \({\mathtt {Band}}\) to themselves and the axiom a to a proof. It is straightforward to prove that this part of the diagram commutes: any two morphisms are identical except for the assignment to the axiom a, and these are equal due to proof irrelevance.Footnote 3
. All of these are of the form \(t=\{{\mathbf {include}}{\;{\mathtt {Band}}},\,a: F\}\), e.g., \({\mathtt {LeftRegularBand}}\) uses \(F=\forall x,z. z\circ x\circ z \doteq z\circ x\). The implicit morphisms map the constants from \({\mathtt {Band}}\) to themselves and the axiom a to a proof. It is straightforward to prove that this part of the diagram commutes: any two morphisms are identical except for the assignment to the axiom a, and these are equal due to proof irrelevance.Footnote 3
4.3 Logic Morphisms
So far, we have assumed all theories use the same fixed meta-theory, e.g.,  in the running examples. But in practice, we usually develop theories heterogeneously by using the weakest possible meta-theory for each module. A strength of
in the running examples. But in practice, we usually develop theories heterogeneously by using the weakest possible meta-theory for each module. A strength of  is that meta-theories are normal theories so that the same structuring formalism can be used for them, e.g., morphisms, includes, pushouts, and implicit morphisms are directly available for meta-theories.
is that meta-theories are normal theories so that the same structuring formalism can be used for them, e.g., morphisms, includes, pushouts, and implicit morphisms are directly available for meta-theories.
For example, consider the example from Fig. 1. We could use first-order logic \({\mathtt {FOL}}\) as the common meta-theory of all theories. But actually the much weaker logic \({\mathtt {Horn}}\) (which uses restricted logical connectives that only allow creating Horn formulas) is sufficient for most of them.
We do not want to declare a direct include \({\mathtt {Horn}}\rightarrow {\mathtt {FOL}}\) for the same reasons as discussed in Sect. 4.2. Instead, we want to give a morphism \({\mathtt {EmbedHorn}}:\) \({\mathtt {Horn}}\rightarrow {\mathtt {FOL}}\), which maps all Horn formula constructors to their \({\mathtt {FOL}}\) counterparts. We can now make \({\mathtt {EmbedHorn}}\) implicit, thus capturing the fact that Horn logic is a fragment of \({\mathtt {FOL}}\).
Moreover, assume we have built the diagram in Fig. 1 using the meta-theory \({\mathtt {Horn}}\) where possible and \({\mathtt {FOL}}\) where necessary. An example for the latter is \({\mathtt {TotalOrder}}\), which also uses \(\vee \). Without implicit morphisms, we would have to write
Here the \({\mathtt {Horn}}\)-theory \({\mathtt {PartialOrder}}\) must be explicitly translated to \({\mathtt {FOL}}\) before including it, which is awkward for users both when writing and reading. But using implicit morphisms and the semantics of Example 9, we can simply write \({\mathbf {include}}{\;{\mathtt {PartialOrder}}}\)—the logic translation remains transparent to the user.
In practice, many logic morphisms are naturally implicit, either because they are includes to begin with or because they represent a canonical logic embedding.
4.4 Transparent Refactoring
A major drawback of using modular theories is that it can preclude transparent refactoring (to insert intermediate theories as mentioned in Sect. 4.2). As an example, we consider a theory \(t=\{{\mathbf {include}}{\;r},{\mathbf {include}}{\;s}\}\), and assume we want to move a constant declaration D for the name n from s to r. This change should be straightforward as it does not change the semantics of t.
However, this is not a local change. It also requires updating every qualified reference from s?n to r?n. Even if the source files always use the unqualified reference n (because the checker is smart enough to dynamically disambiguate them), this still requires a global rebuild to reach a consistent state again. But such references can occur anywhere where t is used, and that may include files that the person who does the refactoring does not know about or does not have access to. One option in this case is to use an extra-logical refactoring tool that propagates such changes. But when managing releases of big libraries, it is often desirable to deprecate the original theories but still ensure backwards compatibility. Then after a transition period the original theories are removed from the library and users are expected to propagate the refactoring.
With implicit morphisms, we can solve this problem by making only the following local changes:
-
1.
We keep r and s as they are.
-
2.
We create a new theory \(r'=\{{\mathbf {include}}{\;r},\,D\}\).
-
3.
We create a new theory \(s'\) that is like s except for deleting the declaration D.
-
4.
We change t to \(t=\{{\mathbf {include}}{\;r'},{\mathbf {include}}{\;s'}\}\).
-
5.
We add implicit morphisms \(s'\rightarrow s\) (map** \(s'?x\) to s?x for all x) and \(s\rightarrow t\) (map** s?n to \(r'?n\) and s?x to \(s'?x\) for all \(x\ne n\)).
The situation before (left) and after (right) refactoring is given below. Note that the right diagram commutes.

Afterwards, t has the desired new structure. But all old references to r and s stay well-formed so that no global changes are needed. Now r and s can be deprecated and eventually removed in favor of \(r'\) and \(s'\).
5 Conclusion and Related Work
Implicit Conversions. The need for implicit conversions has been recognized in many formal systems. In all cases, similar uniqueness constraints are employed as in ours.
Type-level conversions are functions between types such as the conversion from natural numbers to integers. Theory-level conversions are morphisms between theories, like in this paper, or similar constructs. The latter can be seen as a special case of the former: if every theory is seen as the type of its models (as in [MRK18]), then reduction along an implicit morphism \(S\rightarrow T\) induces a conversion from T-models to S-models. Type-level conversions are present in many systems, e.g., the Coq proof assistant [Coq15] or the Scala programming language. The novelty in our approach is to restrict conversions two-fold: firstly to the theory level, secondly to those conversion functions that can be expressed as theory morphisms. This significantly reduces the complexity and permits an elegant logic-independent semantics, while still being practically useful.
Some formal systems support theory-level conversions without explicitly using theory morphisms. This is common in systems that use type classes as an analogue to theories. For example, the sublocale declarations of the proof assistant Isabelle [KWP99] or the deriving declarations of the programming language Haskell can be seen as implicit morphisms even though no primitive concept of morphism objects is employed. Our implicit morphisms yield a simpler and more expressive theory-level conversion system at the price of having an additional primitive concept.
Structuring Theories. In systems that maintain large diagrams of theories, the problems solved by our approach have been recognized for some time. For example, the IMPS system [FGT93] allowed using theory morphisms to retroactively add defined constants to a previously declared theory. This corresponds to a definitional extension with an implicit retraction morphism as in Sect. 4.1.
In [CFK14], the idea of realms was introduced as a way to bundle a set of isomorphic theories and their definitional extensions into a single interface. The paper called for an implementation of realms as a new primitive concept in addition to theories and morphisms. In contrast, the much simpler feature of implicit morphisms achieves very similar goals: realms can be recovered by marking all isomorphisms as implicit and all extensions as definitional.
It remains future to investigate the relationship between implicit morphisms and other generalizations of the set-theoretic notion of inclusion such as factorization or inclusion systems.
Scalability and Sco**. Future work will focus on utilizing and evaluating implicit morphisms in large libraries, i.e., diagrams with thousands of theories and as many implicit morphisms as possible.
In doing so, we will pay particular attention to some problems that implicit conversions can cause at large scale. Users can be confused when implicit conversions are applied that they are not aware of, and different users may also have different preferences for which conversions should be implicit. Moreover, critically, different developments may be incompatible if they introduce different implicit morphisms between the same theories. For those reasons, Scala, for example, only applies implicit conversions that are imported into the current namespace.
We anticipate that these problems will lead to an evolution of our solution that allows more localized control over which morphisms are implicit. Thus, instead of a single global diagram of implicit morphisms, every context may carry its own local one. But we defer this until the current implementation has been used to conduct very large case studies.
Notes
- 1.
Note that we use the syntactic direction for the arrows, e.g., an arrow \(m:S\rightarrow T\) states that any S-expression E (e.g., a sort, term, formula, or proof) can be translated to a T-expression m(E). Models are translated in the opposite direction.
- 2.
The
 tool accepts \((c:=e)\in M^\flat \) even if \((c:E=e')\in S^\flat \). In that case,
tool accepts \((c:=e)\in M^\flat \) even if \((c:E=e')\in S^\flat \). In that case,  checks \(\vdash _T M(e')=e:M(E)\) and puts \(M(c)=e\). This is important for efficiency but not essential for our purposes here.
checks \(\vdash _T M(e')=e:M(E)\) and puts \(M(c)=e\). This is important for efficiency but not essential for our purposes here. - 3.
Our formalization of bands can be found at https://gl.mathhub.info/MMT/exam-ples/blob/devel/source/bands.mmt.
References
Autexier, S., Hutter, D., Mantel, H., Schairer, A.: Towards an evolutionary formal software-development using CASL. In: Bert, D., Choppy, C., Mosses, P.D. (eds.) WADT 1999. LNCS, vol. 1827, pp. 73–88. Springer, Heidelberg (2000). https://doi.org/10.1007/978-3-540-44616-3_5
Clavel, M., Eker, S., Lincoln, P., Meseguer, J.: Principles of Maude. In: Meseguer, J. (ed.) Proceedings of the First International Workshop on Rewriting Logic, vol. 4, pp. 65–89 (1996)
Carette, J., Farmer, W.M., Kohlhase, M.: Realms: a structure for consolidating knowledge about mathematical theories. In: Watt, S.M., Davenport, J.H., Sexton, A.P., Sojka, P., Urban, J. (eds.) CICM 2014. LNCS (LNAI), vol. 8543, pp. 252–266. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08434-3_19
Carette, J., Farmer, W.M., O’Connor, R.: MathScheme: project description. In: Davenport, J.H., Farmer, W.M., Urban, J., Rabe, F. (eds.) CICM 2011. LNCS (LNAI), vol. 6824, pp. 287–288. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22673-1_23
Codescu, M., Horozal, F., Kohlhase, M., Mossakowski, T., Rabe, F.: Project abstract: logic atlas and integrator (LATIN). In: Davenport, J.H., Farmer, W.M., Urban, J., Rabe, F. (eds.) CICM 2011. LNCS (LNAI), vol. 6824, pp. 289–291. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22673-1_24
Coq Development Team: The Coq Proof Assistant: Reference Manual. Technical report, INRIA (2015)
Farmer, W., Guttman, J., Thayer, F.: Little theories. In: Kapur, D. (ed.) Conference on Automated Deduction, pp. 467–581 (1992)
Farmer, W., Guttman, J., Thayer, F.: IMPS: an interactive mathematical proof system. J. Autom. Reason. 11(2), 213–248 (1993)
Goguen, J., Winkler, T., Meseguer, J., Futatsugi, K., Jouannaud, J.: Introducing OBJ. In: Goguen, J., Coleman, D., Gallimore, R. (eds.) Applications of Algebraic Specification using OBJ. Cambridge University Press, Cambridge (1993)
Kammüller, F., Wenzel, M., Paulson, L.C.: Locales – a sectioning concept for Isabelle. In: Bertot, Y., Dowek, G., Théry, L., Hirschowitz, A., Paulin, C. (eds.) TPHOLs 1999. LNCS, vol. 1690, pp. 149–165. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48256-3_11
Mossakowski, T., Maeder, C., Lüttich, K.: The heterogeneous tool set, Hets. In: Grumberg, O., Huth, M. (eds.) TACAS 2007. LNCS, vol. 4424, pp. 519–522. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-71209-1_40
Müller, D., Rabe, F., Kohlhase, M.: Theories as types. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS (LNAI), vol. 10900, pp. 575–590. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94205-6_38
Pfenning, F., Schürmann, C.: System description: Twelf — a meta-logical framework for deductive systems. CADE 1999. LNCS (LNAI), vol. 1632, pp. 202–206. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48660-7_14
Rabe, F.: How to identify, translate, and combine logics? J. Logic Comput. 27(6), 1753–1798 (2017)
Rabe, F., Kohlhase, M.: A scalable module system. Inf. Comput. 230(1), 1–54 (2013)
Sannella, D., Wirsing, M.: A kernel language for algebraic specification and implementation extended abstract. In: Karpinski, M. (ed.) FCT 1983. LNCS, vol. 158, pp. 413–427. Springer, Heidelberg (1983). https://doi.org/10.1007/3-540-12689-9_122
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 IFIP International Federation for Information Processing
About this paper
Cite this paper
Rabe, F., Müller, D. (2019). Structuring Theories with Implicit Morphisms. In: Fiadeiro, J., Țuțu, I. (eds) Recent Trends in Algebraic Development Techniques. WADT 2018. Lecture Notes in Computer Science(), vol 11563. Springer, Cham. https://doi.org/10.1007/978-3-030-23220-7_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-23220-7_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-23219-1
Online ISBN: 978-3-030-23220-7
eBook Packages: Computer ScienceComputer Science (R0)





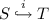 , we can use all S-identifiers in T as if S were included into T. Any
, we can use all S-identifiers in T as if S were included into T. Any  , using S?n as an identifier in T is unambiguous.
, using S?n as an identifier in T is unambiguous. (including the special case
(including the special case  has been defined first and S only later. This is very common because people usually formalize the most important theories (e.g.,
has been defined first and S only later. This is very common because people usually formalize the most important theories (e.g.,  . This either causes T to have redundant axioms or requires a more complex include mechanism that allows T to include S in a way that turns some of S-axioms into theorems.
. This either causes T to have redundant axioms or requires a more complex include mechanism that allows T to include S in a way that turns some of S-axioms into theorems.
 tool accepts
tool accepts  checks
checks 