Modeling Asset Returns with Skewness, Kurtosis, and Outliers

Abstract

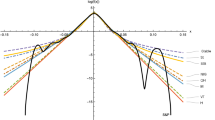
This chapter uses an exponential generalized beta distribution of the second kind (EGB2) to model the returns on 30 Dow Jones industrial stocks. The model accounts for stock return characteristics, including fat tails, peakedness (leptokurtosis), skewness, clustered conditional variance, and leverage effect. The evidence suggests that the error assumption based on the EGB2 distribution is capable of taking care of skewness, kurtosis, and peakedness and therefore is also capable of making good predictions on extreme values. The goodness-of-fit statistic provides supporting evidence in favor of EGB2 distribution in modeling stock returns. This chapter also finds evidence that the leverage effect is diminished when higher moments are considered.

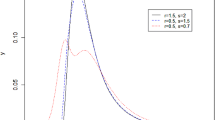
The EGB2 distribution used in this chapter is a four-parameter distribution. It has a closed-form density function and its higher-order moments are finite and explicitly expressed by its parameters. The EGB2 distribution nests many widely used distributions such as normal distribution, log-normal distribution, Weibull distribution, and standard logistic distribution.

Appendix 1

80.1.1 Delta Method and Standard Errors of the Skewness and Kurtosis Coefficients of the EGB2 Distribution

The delta method, in its essence, expands a function of a random variable about its mean, usually with a one-step Taylor approximation, and then takes the variance. For example, if we want to approximate the variance of G(x) where x is a random variable with mean μ and G(x) is differentiable, we can try

$$ G(x)\approx G\left(\mu \right)+\left(x-\mu \right)G\prime \left(\mu \right) $$

(80.9)

so that

$$ \mathrm{Var}\left(G(x)\right)\approx G\prime {\left(\mu \right)}^2\mathrm{Var}(x) $$

(80.10)

where G′() = dG/dX. This is a good approximation only if x has a high probability of being close enough to its mean so that the Taylor approximation is still good.

The nth central moments of the EGB2 distribution is given by

$$ \mathrm{The}\ \mathrm{nth}\ \mathrm{moment}={\sigma}^n\left({\psi}^{n-1}(p)+{\left(-1\right)}^n{\psi}^{n-1}(q)\right) $$

(80.11)

where ψⁿ is nth order a polygamma function. Correspondingly, the skewness coefficient is given by

$$ \mathrm{Skewness}=g\left(p,q\right)=\frac{\psi {\prime\prime} (p)-\psi {\prime\prime} (q)}{{\left(\psi \prime (p)+\psi \prime (q)\right)}^{1.5}} $$

(80.12)

The variance of the skewness coefficient by the delta method is given by

$$ \mathrm{Var}\left(\mathrm{Skewness}\right)={g}_p^{\hbox{'}}{\left(p,q\right)}^2\mathrm{var}(p)+{g}_q^{\hbox{'}}{\left(p,q\right)}^2\mathrm{var}(q)+2{g}_p^{\hbox{'}}\left(p,q\right){g}_q^{\hbox{'}}\left(p,q\right)\mathrm{cov}\left(p,q\right) $$

(80.13)

where

$$ {g}_p^{\prime}\left(p,q\right)=\frac{\psi \prime \prime \prime (p)\left(\psi \prime (p)+\psi \prime (q)\right)-1.5\psi {\prime\prime} (p)\left(\psi {\prime\prime} (p)-\psi {\prime\prime} (q)\right)}{{\left(\psi \prime (p)+\psi \prime (q)\right)}^{2.5}} $$

(80.14)

$$ {g}_q^{\hbox{'}}\left(p,q\right)=\frac{-\psi \prime \prime \prime (q)\left(\psi \prime (p)+\psi \prime (q)\right)-1.5\psi {\prime\prime} (q)\left(\psi {\prime\prime} (p)-\psi {\prime\prime} (q)\right)}{{\left(\psi \prime (p)+\psi \prime (q)\right)}^{2.5}} $$

(80.15)

Similarly, the excess kurtosis coefficient is given by

$$ \mathrm{Kurtosis}=h\left(p,q\right)=\frac{\psi \prime \prime \prime (p)+\psi \prime \prime \prime (q)}{{\left(\psi \prime (p)+\psi \prime (q)\right)}^2} $$

(80.16)

The variance of the kurtosis coefficient by the delta method is given by

$$ \mathrm{Var}\left(\mathrm{Kurtosis}\right)={h}_p^{\prime }{\left(p,q\right)}^2\mathrm{var}(p)+{h}_q^{\prime }{\left(p,q\right)}^2\mathrm{var}(q)+2{h}_p^{\prime}\left(p,q\right){h}_q^{\prime}\left(p,q\right)\mathrm{cov}\left(p,q\right) $$

(80.17)

where

$$ {h}_p^{\prime}\left(p,q\right)=\frac{\psi \prime \prime \prime \prime (p)\left(\psi \prime (p)+\psi \prime (q)\right)-2\psi {\prime\prime} (p)\left(\psi \prime \prime \prime (p)+\psi \prime \prime \prime (q)\right)}{{\left(\psi \prime (p)+\psi \prime (q)\right)}^3} $$

(80.18)

$$ {h}_q^{\prime}\left(p,q\right)=\frac{\psi \prime \prime \prime \prime (q)\left(\psi \prime (p)+\psi \prime (q)\right)-2\psi {\prime\prime} (q)\left(\psi \prime \prime \prime (p)+\psi \prime \prime \prime (q)\right)}{{\left(\psi \prime (p)+\psi \prime (q)\right)}^3} $$

(80.19)

In the equations above, high-order polygamma functions are involved. A polygamma function is the nth normal derivative of the logarithmic derivative of Γ(z):

$$ {\psi}^n(z)=\frac{d^{n+1}}{d{z}^{n+1}} \ln \left(\Gamma (z)\right) $$

(80.20)

which, for n > 0, can be written as

$$ {\psi}^n(z)={\left(-1\right)}^{n+1}n!{\displaystyle \sum_{k=0}^{\infty}\frac{1}{{\left(z+k\right)}^{n+1}}} $$

(80.21)

which is used to calculate polygamma functions in this chapter.

Note: This appendix is based on the paper by Wang et al. (2001). However, there are typos and errors in that paper. The standard deviation formula for skewness used by Wang et al. (2001) is incorrect (see g′q(p,q) equation in the paper at http://www.econ.queensu.ca/jae/2001-v16.4/wang-fawson-barrett-mcdonald/Appendix4_delta_derivations.pdf). We therefore provide this appendix. Accordingly, as we reviewed and replicated that paper by using the data supplied by the Journal of Applied Econometrics, the EGB2 distribution doesn’t remove the skewness problem completely as shown in their Table 3. In addition, there is a computational error in the JPY series, so that its kurtosis has not been resolved either.