Value-at-Risk Estimation via a Semi-parametric Approach: Evidence from the Stock Markets

Abstract

This study utilizes the parametric approach (GARCH-based models) and the semi-parametric approach of Hull and White (Journal of Risk 1: 5–19, 1998) (HW-based models) to estimate the Value-at-Risk (VaR) through the accuracy evaluation of accuracy for the eight stock indices in Europe and Asia stock markets. The measure of accuracy includes the unconditional coverage test by Kupiec (Journal of Derivatives 3: 73–84, 1995) as well as two loss functions, quadratic loss function, and unexpected loss. As to the parametric approach, the parameters of generalized autoregressive conditional heteroskedasticity (GARCH) model are estimated by the method of maximum likelihood and the quantiles of asymmetric distribution like skewed generalized student’s t (SGT) can be solved by composite trapezoid rule. Sequentially, the VaR is evaluated by the framework proposed by Jorion (Value at Risk: the new benchmark for managing financial risk. New York: McGraw-Hill, 2000). Turning to the semi-parametric approach of Hull and White (Journal of Risk 1: 5–19, 1998), before performing the traditional historical simulation, the raw return series is scaled by a volatility ratio where the volatility is estimated by the same procedure of parametric approach. Empirical results show that the kind of VaR approaches is more influential than that of return distribution settings on VaR estimate. Moreover, under the same return distributional setting, the HW-based models have the better VaR forecasting performance as compared with the GARCH-based models. Furthermore, irrespective of whether the GARCH-based model or HW-based model is employed, the SGT has the best VaR forecasting performance followed by student’s t, while the normal owns the worst VaR forecasting performance. In addition, all models tend to underestimate the real market risk in most cases, but the non-normal distributions (student’s t and SGT) and the semi-parametric approach try to reverse the trend of underestimating.

Appendices

Appendix 1: The Left-Tailed Quantiles of the Standardized SGT

The standardized SGT distribution was derived by Lee and Su (2011) and expressed as follows:

$$ \mathrm{f}\left({\upvarepsilon}_{\mathrm{t}}\right)=\mathrm{C}{\left\{1+\frac{{\left|{\upvarepsilon}_{\mathrm{t}}+\updelta \right|}^{\upkappa}}{{\left[1+\mathrm{sign}\left({\upvarepsilon}_{\mathrm{t}}+\updelta \right)\uplambda \right]}^{\upkappa}{\uptheta}^{\upkappa}}\right\}}^{-\frac{\mathrm{n}+1}{\upkappa}} $$

(51.17)

where $\uptheta =\frac{1}{\mathrm{S}\left(\uplambda \right)}\mathrm{B}{\left(\frac{1}{\upkappa},\frac{\mathrm{n}}{\upkappa}\right)}^{\frac{1}{2}}\mathrm{B}{\left(\frac{3}{\upkappa},\frac{\mathrm{n}-2}{\upkappa}\right)}^{-\frac{1}{2}},\mathrm{S}\left(\uplambda \right)=\sqrt{1+3{\uplambda}^2-4{\mathrm{A}}^2{\uplambda}^2}$,

$\mathrm{A}=\mathrm{B}\left(\frac{2}{\upkappa},\frac{\mathrm{n}-1}{\upkappa}\right)\mathrm{B}{\left(\frac{1}{\upkappa},\frac{\mathrm{n}}{\upkappa}\right)}^{-0.5}\mathrm{B}{\left(\frac{3}{\upkappa},\frac{\mathrm{n}-2}{\upkappa}\right)}^{-0.5}$, $\updelta =\frac{2\uplambda \mathrm{A}}{\mathrm{S}\left(\uplambda \right)}$, $\mathrm{C}=\frac{\upkappa}{2\uptheta}\mathrm{B}{\left(\frac{1}{\upkappa},\frac{\mathrm{n}}{\upkappa}\right)}^{-1}$

where κ, n, and λ are scaling parameters and C and θ are normalizing constants ensuring that f(•) is a proper p.d.f. The parameters κ and n control the height and tails of density with constraints κ > 0 and n > 2, respectively. The skewness parameter λ controls the rate of descent of the density around the mode of ε _t with − 1 < λ < 1. In the case of positive (resp. negative) skewness, the density function skews toward the right (resp. left). Sign is the sign function, and B(•) is the beta function. The parameter n has the degrees of freedom interpretation in case λ = 0 and κ = 2. Particularly, the SGT distribution generates the student’s t distribution for λ = 0 and κ = 2. Moreover, the SGT distribution generates the normal distribution for λ = 0, κ = 2, and n = ∞.

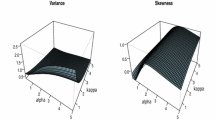
As observed from Table 51.2, the shape parameters in SGT distribution, the fat-tail parameter (n) ranges from 4.9846 (KLSE) to 21.4744 (KOSPI), and the fat-tail parameter (κ) is between 1.5399 (KOSPI) and 2.3917 (Bombay). The skewness parameter (λ) ranges from −0.1560 (Bombay) to −0.0044 (KLSE). Therefore, the left-tailed quantiles of the SGT distribution with various combinations of shape parameters (−0.15 ≤ λ ≤ 0.05; 1.0 ≤ κ ≤ 2.0; n = 10) at alternate levels are obtained by the composite trapezoid rule and are listed in Table 51.6. Moreover, Fig. 51.3 depicts the left-tailed quantiles surface of SGT (versus normal) distribution with various combinations of shape parameters (−0.25 ≤ λ ≤ 0.25; 0.8 ≤ κ ≤ 2.0;n = 10 and 20) at 10 %, 5 %, 1 %, and 0.5 % levels. Notably, F_c(ε _t ;κ = 2, λ = 0, n = ∞) where c = 0.1, 0.05, 0.01, and 0.005 in Fig. 51.3 represents the left-tailed quantiles of normal distribution at 10 %, 5 %, 1 %, and 0.5 % levels, which is −1.28155, −1.64486, −2.32638, and −2.57613, respectively.

Fig. 51.3

The left-tailed quantiles of SGT distribution with n = 10, 20, and various combinations (κ, λ). (a) 10 %, (b) 5 %, (c) 1 %, (d) 0.5 % confidence levels

Table 51.6 The left-tailed quantiles of SGT distribution with n = 10 and various combinations (κ, λ) at alternate levels

Appendix 2: The Procedure of Parametric VaR Approach

The parametric method is very popular because the only variables you need to do the calculation are the mean and standard deviation of the portfolio, indicating the simplicity of the calculations. Moreover, from the literatures’ review mentioned above, numerous studies focused on the parametric approach of the GARCH family variance specifications to estimate the VaR. Furthermore, numerous time series data of financial assets appear to exhibit autocorrelated and volatility clustering, and the unconditional distribution of those returns displays leptokurtosis and a moderate amount of skewness. This study thus considers the applicability of the GARCH(1,1) model with three conditional distributions (the normal, student’s t, and SGT distributions) to estimate the corresponding volatility in terms of different stock indices, then employs the framework of Jorion (2000) to evaluate the VaR of parametric approach. We take an example of the GARCH-SGT model. The methodology of parametric VaR approach is based on a rolling window procedure. The window size is fixed at 2,000 observations. More specifically, the procedure is conducted in the following manner:

• Step 1: For each data series, using the econometric package of WinRATS 6.1, the parameters are estimated with a sample of 2,000 daily returns by quasi-maximum likelihood estimation (QMLE) of log-likelihood function such as Eq. 51.10 and by the BFGS optimization algorithm. Thus, with ψ = [μ, ω, α, β, κ, λ, n], the vector of parameters is estimated. The empirical results of GARCH-SGT model are listed in Table 51.2 for all stock indices surveyed in this paper. As to the empirical results of GARCH-N and GARCH-T models, they are also provided by the same approach.

• Step 2: Based on the framework of the parametric techniques (Jorion 2000), the 1-day-ahead VaR based on GARCH-SGT model can be calculated by Eq. 51.11. Then the one-step-ahead VaR forecasts are compared with the observed returns, and the comparative results are recorded for subsequent evaluation using statistical tests.

• Step 3: The estimation period is then rolled forwards by adding one new day and drop** the most distant day. By replicating step 1 and step 2, the vector of parameters is estimated, and then the 1-day-ahead VaR can be calculated for the next 500 days.

• Step 4: For the out-sample period (500 days), via the comparable results between the one-step-ahead VaR forecasts and the observed returns, the 1-day-ahead BLF, QLF, and UL can be calculated by using Eqs. 51.13, 51.14 and 51.16. On the other hand, the unconditional coverage test, LR_uc, is evaluated by employing Eq. 51.15. Thereafter, with regard to the GARCH-based models with alternate distributions (GARCH-N, GARCH-T, and GARCH-SGT), the unconditional coverage test (LR_uc) and three loss functions (failure rate, AQLF, and UL) are obtained and are reported in the left panel of Tables 51.3, 51.4 and 51.5 for 95 %, 99 %, and 99.5 % levels.

Appendix 3: The Procedure of Semi-parametric VaR Approach

In this paper, we use the approach proposed by Hull and White (1998) as a representative of the semi-parametric approach. This method mainly couples a weighting scheme of volatility with the traditional historical simulation. Hence, it can be regarded as a straightforward extension of traditional historical simulation. The weighting scheme of volatility is expressed as follows. Instead of using the actual historical percentage changes in market variables for the purposes of calculating VaR, we use historical changes that have been adjusted to reflect the ratio of the current daily volatility to the daily volatility at the time of the observation and assume that the variance of each market variable during the period covered by the historical data is monitored using a GARCH-based models. We take an example of the HW-SGT model. This methodology is explained in the following five steps:

• Step 1: For each data series, using the econometric package of WinRATS 6.1, the parameters are estimated with a sample of 2,000 daily returns by quasi-maximum likelihood estimation (QMLE) of log-likelihood function such as Eq. 51.10 and by the BFGS optimization algorithm. Thus, with ψ = [μ, ω, α, β, κ, λ, n], the vector of parameters is estimated. This step is the same as the first step of parametric approach. Consequently, a series of daily volatility estimates, {σ₁, σ₂, σ₃,......, σ_t=T}, are obtained where T is the number of estimated samples and equals 2,000 in this study.

• Step 2: The modified return series are obtained by the raw return series multiplied by the ratio of the current daily volatility to the daily volatility at the time of the observation, σ_T/σ_i. That is, the modified return series are expressed as {r₁ ^*, r₂ ^*, r₃ ^*,......, r_t=T ^*}, where r_i ^* = r_i(σ_T/σ_i).

• Step 3: Resort this modified return series ascendingly to achieve the empirical distribution. Thus, VaR is the percentile that corresponds to the specified confidence level. Then the one-step-ahead VaR forecasts are compared with the observed returns, and the comparative results are recorded for subsequent evaluation using statistical tests.

• Step 4: The estimation period is then rolled forwards by adding one new day and drop** the most distant day. By replicating steps 1–3, the vector of parameters is estimated, and then the 1-day-ahead VaR can be calculated for the next 500 days. This step is the same as the third step of parametric approach.

• Step 5: For the out-sample period (500 days), via the comparable results between the one-step-ahead VaR forecasts and the observed returns, the 1-day-ahead BLF, QLF, and UL can be calculated by using Eqs. 51.13, 51.14, and 51.16. On the other hand, the unconditional coverage test, LR_uc, is evaluated by employing Eq. 51.15. Thereafter, with regard to HW-based models with alternate distributions (HW-N, HW-T, and HW-SGT), the unconditional coverage test (LR_uc) and three loss functions (failure rate, AQLF, and UL) are obtained and are reported in the right panel of Tables 51.3, 51.4 and 51.5 for 95 %, 99 %, and 99.5 % levels.