Pressure Transient Characteristics of Highly Deviated Wells in Fractured-Vuggy Carbonate Gas Reservoirs

Abstract

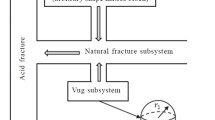
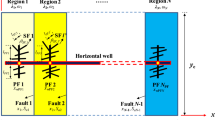
More and more attention has been paid to the study of flow properties in fractured-vuggy reservoirs because lots of such reservoirs have been found worldwide with significant gas production and reserves. In order to improve carbonate gas reservoir production, highly deviated wells (HDW) are widely used in the field. However, it is very difficult to consider the complex pore structure of fractured-vuggy reservoirs and evaluate the pressure transient behaviors of HDW. This paper presents a semi-analytical model that analyzed the pressure behavior of HDW in fractured-vuggy carbonate gas reservoirs which consist of fractures, vugs and matrix. Introducing pseudo-pressure; Fourier transformation, Laplace transformation, and Stehfest numerical inversion were employed to establish a point source and line source solutions. Furthermore, the validity of the proposed model was verified by comparing with two existing pressure transient models. Then the flow characteristics were analyzed thoroughly by examining the pressure derivative curve which can be divided into five flow stages. The physical meanings of the model parameters were analyzed through sensitivity analysis. Finally, a field case was successfully used to show the application of the proposed semi-analytical model. The study contributes to the highly efficient evaluation of the pressure transient behaviors for HDW in fractured-vuggy carbonate gas reservoirs.

Appendices

Appendix A. Calculation of Pseudo-pressure

In Eqs. (1)–(7), $m_{f}$, $m_{m}$, $m_{c}$ is the pseudo-pressure of the fracture system, matrix system and vugs system, respectively, $MPa/s$. The pseudo-pressure can be given as follows:

$$ m = \int_{0}^{p} {\frac{2p}{{\mu_{g} Z}}} dp $$

(A.1)

Appendix B. Calculation of Continuous Point Source Solution

Equations (8)–(14) can be transformed into Laplace domain by the Laplace transformation.

The dimensionless governing equations of fractures, matrix and vugs systems in the Laplace domain are as follows:

$$ \frac{1}{{r_{D} }}\frac{\partial }{{\partial r_{D} }}(r_{D} \frac{{\partial \overline{m}_{fD} }}{{\partial r_{D} }}) + \frac{{\partial^{2} \overline{m}_{fD} }}{{\partial z_{D}^{2} }} = \omega_{f} s\overline{m}_{fD} - \lambda_{m} (\overline{m}_{mD} - \overline{m}_{fD} ) - \lambda_{c} (\overline{m}_{cD} - \overline{m}_{fD} ) $$

(B.1)

$$ \omega_{m} s\overline{m}_{mD} = \lambda_{m} (\overline{m}_{fD} - \overline{m}_{mD} ) $$

(B.2)

$$ \omega_{c} s\overline{m}_{cD} = \lambda_{c} (\overline{m}_{fD} - \overline{m}_{cD} ) $$

(B.3)

The outer boundary condition is transformed as:

$$ \left. {\frac{{\partial \overline{m}_{jD} }}{{\partial r_{D} }}} \right|_{{r_{D} = r_{eD} }} = 0,\;\;\;(j = f,m,c) $$

(B.4)

The inner boundary condition is transformed as:

$$ \begin{array}{*{20}l} {\mathop {\lim }\limits_{{\varepsilon_{D} \to 0}} \left( {\mathop {\lim }\limits_{{r_{D} \to 0}} \int_{{z_{wD} - {{\varepsilon_{D} } \mathord{\left/ {\vphantom {{\varepsilon_{D} } 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{z_{{w_{D} }} + {{\varepsilon_{D} } \mathord{\left/ {\vphantom {{\varepsilon_{D} } 2}} \right. \kern-\nulldelimiterspace} 2}}} {r_{D} \frac{{\partial \overline{m}_{fD} }}{{\partial r_{D} }}dz_{D} } } \right) = \left\{ \begin{gathered} - \frac{{h_{D} }}{s} \hfill \\ 0 \hfill \\ \end{gathered} \right.\;\;\;} \hfill & \begin{gathered} \left| {z_{D} - z_{wD} } \right| \le {{\varepsilon_{D} } \mathord{\left/ {\vphantom {{\varepsilon_{D} } 2}} \right. \kern-\nulldelimiterspace} 2} \hfill \\ \left| {z_{D} - z_{wD} } \right|{{ > \varepsilon_{D} } \mathord{\left/ {\vphantom {{ > \varepsilon_{D} } 2}} \right. \kern-\nulldelimiterspace} 2} \hfill \\ \end{gathered} \hfill \\ \end{array} $$

(B.5)

The top and bottom boundaries are transformed as:

$$ \left. {\frac{{\partial \overline{m}_{fD} }}{{\partial z_{D} }}} \right|_{{z_{D} = 0}} = \left. {\frac{{\partial \overline{m}_{fD} }}{{\partial z_{D} }}} \right|_{{z_{D} = h_{D} }} = 0 $$

(B.6)

Where

$$ \overline{m}_{jD} = \int_{0}^{\infty } {e^{{ - st_{D} }} m_{jD} (t_{D} } )dt_{D} ,\;\;\;(j = f,m,c) $$

(B.7)

To eliminate the variable $z_{D}$ in the governing equation, Eqs. (B.1)–(B.5) can be transformed by Fourier cosine transform. The Fourier cosine transform and inverse Fourier cosine transform are given as follows:

$$ \widehat{m}_{jD} = \int_{0}^{{h_{D} }} {m_{jD} \cos \left( {\frac{{n\pi z_{D} }}{{h_{D} }}} \right)} dh_{D} ,\;\;\;(j = f,m,c) $$

(B.8)

$$ m_{jD} = \sum\limits_{n} {\widehat{m}_{jD} \frac{{\cos \left( {\frac{{n\pi z_{D} }}{{h_{D} }}} \right)}}{N(n)}} ,\;\;\;(j = f,m,c) $$

(B.9)

Where

$$ \begin{gathered} \begin{array}{*{20}l} {N(n) = \int_{0}^{{h_{D} }} {\cos^{2} \left( {\frac{{n\pi z_{D} }}{{h{}_{D}}}} \right)dz_{D} } = \left\{ \begin{gathered} h_{D} \hfill \\ \frac{{h_{D} }}{2} \hfill \\ \end{gathered} \right.} \hfill & \begin{aligned} & n = 0 \\ & n = 1,2,3 \ldots \\ \end{aligned} \hfill \\ \end{array} \hfill \\ \hfill \\ \end{gathered} $$

(B.10)

By employing the Fourier cosine transform (Eq. (B8)), Eqs. (B.1)–(B.5) can be transformed as follows:

$$ \frac{{d^{2} \widehat{{\overline{m} }}_{fD} }}{{dr_{D}^{2} }} + \frac{1}{{r_{D} }}\frac{{d\widehat{{\overline{m} }}_{fD} }}{{dr_{D} }} - \left[ {u_{n}^{2} + sf(s)} \right]\widehat{{\overline{m} }}_{fD} = 0 $$

(B.11)

Where

$$ u_{n} = \frac{n\pi }{{h_{D} }} $$

(B.12)

$$ f(s) = w_{f} + \frac{{\lambda_{c} \omega_{c} }}{{\lambda_{c} + \omega_{c} s}} + \frac{{\lambda_{m} \omega_{m} }}{{\lambda_{m} + \omega_{m} s}} $$

(B.13)

The outer boundary condition is transformed as:

$$ \left. {\frac{{\partial \widehat{{\overline{m} }}_{jD} }}{{\partial r_{D} }}} \right|_{{r_{D} = r_{eD} }} = 0,\;\;\;(j = f,m,c) $$

(B.14)

The inner boundary condition is transformed as:

$$ \mathop {\lim }\limits_{{r_{D} \to 0}} r_{D} \frac{{\partial \widehat{{\overline{m} }}_{fD} }}{{\partial r_{D} }} = - \frac{{h_{D} }}{s}\cos (u_{n} z_{wD} ) $$

(B.15)

Then Eq. (B.11) can be transformed to a modified Bessel function of zero order, like this:

$$ \begin{aligned} & \left( {r_{D} \sqrt {u_{n}^{2} + sf(s)} } \right)^{2} \frac{{d^{2} \widehat{{\overline{m} }}_{fD} }}{{d\left( {r_{D} \sqrt {u_{n}^{2} + sf(s)} } \right)^{2} }} \\ & + \,r_{D} \sqrt {u_{n}^{2} + sf(s)} \frac{{d\widehat{{\overline{m} }}_{fD} }}{{d\left( {r_{D} \sqrt {u_{n}^{2} + sf(s)} } \right)}} - r_{D}^{2} \left( {u_{n}^{2} + sf(s)} \right)\widehat{{\overline{m} }}_{fD} = 0 \\ \end{aligned} $$

(B.16)

The general solution of Eq. (B.16) is given as follows:

$$ \widehat{{\overline{m} }}_{fD} = A_{0} I_{0} \left[ {r_{D} \sqrt {u_{n}^{2} + sf(s)} } \right] + B_{0} K_{0} \left[ {r_{D} \sqrt {u_{n}^{2} + sf(s)} } \right] $$

(B.17)

Based on the outer and inner boundary conditions (Eq. (B14)–(B.15)), the solution in Laplace domain can be obtained by inverse Fourier cosine transform as follows:

$$ \begin{aligned} \overline{m} _{{fD}} = & \;\frac{1}{s}\left[ {\frac{{K_{1} (r_{{eD}} \sqrt {sf(s)} )}}{{I_{1} (r_{{eD}} \sqrt {sf(s)} )}}I_{0} (r_{D} \sqrt {sf(s)} ) + K_{0} (r_{D} \sqrt {sf(s)} )} \right] \\ & + \,\frac{2}{s}\sum\limits_{{n = 1}}^{\infty } {\left[ {\frac{{K_{1} (r_{{eD}} \sqrt {u_{n}^{2} + sf(s)} )}}{{I_{1} (r_{{eD}} \sqrt {u_{n}^{2} + sf(s)} )}}I_{0} (r_{D} \sqrt {u_{n}^{2} + sf(s)} )} \right.} \\ & \left. { + \;\;K_{0} (r_{D} \sqrt {u_{n}^{2} + sf(s)} )} \right]\cos (\mu _{n} z_{{wD}} )\cos (\mu _{n} z_{D} ) \\ \end{aligned} $$

(B.18)