Abstract
A thought experiment is proposed to demonstrate the existence of a gravitational, vector Aharonov-Bohm effect. We begin the analysis starting from four Maxwell-like equations for weak gravitational fields interacting with slowly moving matter. A connection is made between the gravitational, vector Aharonov-Bohm effect and the principle of local gauge invariance for nonrelativistic quantum matter interacting with weak gravitational fields. The compensating vector fields that are necessitated by this local gauge principle are shown to be incorporated by the DeWitt minimal coupling rule. The nonrelativistic Hamiltonian for weak, time-independent fields interacting with quantum matter is then extended to time-dependent fields, and applied to the problem of the interaction of radiation with macroscopically coherent quantum systems, including the problem of gravitational radiation interacting with superconductors. But first we examine the interaction of EM radiation with superconductors in a parametric oscillator consisting of a superconducting wire placed at the center of a high Q superconducting cavity driven by pump microwaves. Some room-temperature data will be presented demonstrating the splitting of a single microwave cavity resonance into a spectral doublet due to the insertion of a central wire. This would represent an unseparated kind of parametric oscillator, in which the signal and idler waves would occupy the same volume of space. We then propose a separated parametric oscillator experiment, in which the signal and idler waves are generated in two disjoint regions of space, which are separated from each other by means of an impermeable superconducting membrane. We find that the threshold for parametric oscillation for EM microwave generation is much lower for the separated configuration than the unseparated one, which then leads to an observable dynamical Casimir effect. We speculate that a separated parametric oscillator for generating coherent GR microwaves could also be built. [Editor’s note: for a video of the talk given by Prof. Chiao at the Aharonov-80 conference in 2012 at Chapman University, see quantum.chapman.edu/talk-20.]
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
In the gravitational version of Maxwell’s equations 14.1)–(14.4) and the gravitational Lorentz force (14.7), we are following the conventions of [10]. It should be noted that in the literature, there are several different versions of the gravitational Maxwell equations and gravitational Lorentz equation that differ by factors of 2 in various places (see, for example, [16] and [17]). It is not clear that the various formulations given in [11–17] are entirely consistent with one another. However, for the regime considered here, where we will use 14.1)–(14.4) with the quasi-static approximation in which the time derivatives of the gravito-electric and gravito-magnetic vector fields in 14.2) and (14.4) vanish, the various conventions of [10–17] agree.
One should also point out that writing (14.1)–(14.4) in terms of vector fields is questionable, since while electromagnetism consists of vector interactions, gravity consists of tensor interactions. Thus, instead of vector gravito-electric and gravito-magnetic fields, it would be better to write out the gravitational version of Maxwell’s equations and the gravitational Lorentz force equation in terms of tensor fields. This approach has been advocated recently [6–8] in terms of tendex and vortex fields. A recent review [9] formulates the gravitational version of Maxwell’s equations and the gravitational version of the Lorentz force equation by contracting the tensor fields, which do not vanish in any reference frame, to vector fields, which can transformed away by gauge choice. However, as before, for the present goals of this paper and in the regimes under which we will use the vector gravitational Maxwell equations, this distinction will not be necessary.
- 2.
The constant ε g is determined by the Newtonian limit of (14.1), which must yield Newton’s law of gravitation, with Newton’s constant G determined by Cavendish’s experiment.
- 3.
The constant μ g is defined in this way in order to obtain the gravitational version of Ampere’s law given in (14.8).
- 4.
We follow the notation and sign conventions of MTW [44], i.e., Greek indices denote space-time indices running from 0 to 3; Latin indices denote spatial indices running from 1 to 3; repeated indices are summed; the signature of the Minkowski metric is diag(−1,+1,+1,+1).
- 5.
It should be noted that the use of the time-dependent gauge in which (h(r,t)) i =ch 0i (r,t)≠0 in this context is only considered for fields within matter, and not in vacuum, where the time-dependent transverse-traceless gauge would be more appropriate.
- 6.
Note that the application of a magnetic field to any system of particles with a given charge-to-mass ratio is equivalent, by Larmor’s theorem, to rotating the system at the Larmor angular frequency. Thus there exists a natural connection between the A and h fields in the proposed experiments in Figs. 14.2 and 14.5.
- 7.
If the electrostatic charge +q on the left side of the membrane were to be sufficiently large (i.e., greater than around 20 picocoulombs; see Appendix B of [33]), so that the membrane becomes extremely tightly coupled to the “single” Fabry-Perot cavity mode on the left side of the membrane, which would happen if this cavity were to be excited in an appropriate transverse magnetic mode, then the mechanical dynamics of the membrane would be “slaved” to the electromagnetic dynamics of this “signal” frequency cavity. For then the displacement of the membrane would be completely determined by Newton’s equation of motion (14.55), so that there results a fixed relationship between the instantaneous longitudinal electric field and the instantaneous membrane displacement, which is given by
$$\begin{aligned} ( \varepsilon_{\varOmega} ) _{s}=-\frac{q ( \mathcal {E}_{z} ) _{s}}{m\omega_{s}^{2}} \end{aligned}$$(14.73)where \(( \mathcal{E}_{z} ) _{s}\) is the complex amplitude of the longitudinal electric field of the transverse magnetic mode at the “signal” frequency ω s of the “single” Fabry-Perot cavity and (ε Ω ) s is the complex amplitude of the displacement of the membrane, which oscillates at the same frequency ω s . In this way, the mechanical vibration frequency Ω of the membrane would be forced to become identical to the microwave frequency ω s of this cavity, and the kinetic energy of the mechanical vibrational motion would be forced to become identical to the electromagnetic energy stored inside this cavity, because these two degrees of freedom would be so tightly coupled to each other that they would no longer be independent degrees of freedom.
- 8.
Instead of a solid SC membrane, one could use a grid of fine SC wires, for example, four fine SC wires arranged in a pattern similar to the number sign “#”, in order to reduce the mass, and thus the threshold.
References
M.A. Hohensee, B. Estey, P. Hamilton, A. Zeilinger, H. Müller, Force-free gravitational redshift: proposed gravitational Aharonov-Bohm experiment. Phys. Rev. Lett. 108, 230404 (2012). Here we consider a thought experiment to see the vector gravitational AB effect instead of the scalar gravitational AB effect.
Y. Aharonov, G. Carmi, Quantum aspects of the equivalence principle. Found. Phys. 3, 493 (1973)
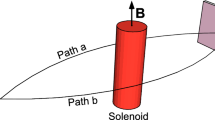
E.G. Harris, The gravitational Aharonov-Bohm effect with photons. Am. J. Phys. 64, 378 (1996). Here we consider the AB effect with electrons rather than photons. The AB effect with photons could be understood entirely classically in terms of classical EM waves diffracting around a “solenoid.” However, no such classical explanation would exist for the electron interference experiment described in Fig. 14.1
J.M. Cohen, B. Mashhoon, Standard clocks, interferometry, and gravitomagnetism. Phys. Lett. A 181, 353 (1993)
A. Tartaglia, Gravitational Aharonov-Bohm effect and gravitational lensing. gr-qc/0003030
R. Owen et al., Frame-dragging vortexes and tidal tendexes attached to colliding black holes: visualizing the curvature of spacetime. Phys. Rev. Lett. 106, 151101 (2011). ar**v:1012.4869
D.A. Nichols et al., Visualizing spacetime curvature via frame-drag vortexes and tidal tendexes: general theory and weak-gravity applications. Phys. Rev. D 84, 124014 (2011). ar**v:1108.5486
A. Zimmerman, D.A. Nichols, F. Zhang, Classifying the isolated zeros of asymptotic gravitational radiation by tendex and vortex lines. Phys. Rev. D 84, 044037 (2011). ar**v:1107.2959
R.H. Price, J.W. Belcher, D.A. Nichols, Comparison of electromagnetic and gravitational radiation; what we can learn about each from the other. ar**v:1212.4730
M. Thorsbud, Post-Newtonian methods and the gravito-electromagnetic analogy. Master’s Thesis, Department of Physics, University of Oslo (2010), p. 56
V.B. Braginsky, C.M. Caves, K.S. Thorne, Laboratory experiments to test relativistic gravity. Phys. Rev. D 15, 2047 (1977)
R.L. Forward, General relativity for the experimentalist. Proc. IRE 49, 892 (1961)
A. Tartaglia, M.L. Ruggiero, Gravito-electromagnetism versus electromagnetism. Eur. J. Phys. 25, 203 (2004)
Section 4.4 in [18]
M. Agop, C.Gh. Buzea, P. Nica, Local gravitoelectromagnetic effects on a superconductor. Physica C 339, 130 (2000)
B. Mashhoon, F. Gronwald, H. Lichtenegger, Gravitomagnetism and the clock effect. Lect. Notes Phys. 562, 83 (2001)
A. Tartaglia, M.L. Ruggiero, Gravitoelectromagnetism versus electromagnetism. Eur. J. Phys. 25, 203 (2004), and Sect. 4.4 of [18]
R.M. Wald, General Relativity (University of Chicago Press, Chicago, 1984)
H. Weyl, The Theory of Groups and Quantum Mechanics (Dover, New York, 1950). (The meaning of the arrow in “a→b” is that “a is to be replaced by b in all the following equations.”)
B.S. In, DeWitt’s paper, “Superconductors and gravitational drag”. Phys. Rev. Lett. 16, 1092 (1966), the minimal coupling rule (14.20) was derived from the principle of general covariance which is behind all metric theories of gravity. This principle was applied to a classical, relativistic, spinless point particle, with the rule (14.20) emerging in the limit of low velocities and weak fields
G. Papini, A test of general relativity by means of superconductors. Phys. Lett. 23, 418 (1966)
G. Papini, Detection of inertial effects using superconducting interferometers. Phys. Lett. 24A, 32 (1967)
L.D. Landau, E.M. Lifshitz, The Classical Theory of Fields, 4th edn., vol. 2 (Butterworth-Heinemann, Stoneham, 2000)
M.V. Berry, Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 392, 45 (1984)
S.B. Felch, J. Tate, B. Cabrera, J.T. Anderson, Precise determination of h/m e using a rotating, superconducting ring. Phys. Rev. B 31, 7006 (1985). There remain some small, unexplained discrepancies for the inferred electron mass, which are probably due to some unknown systematic errors in the experiment.
M.D. Semon, Experimental verification of an Aharonov-Bohm effect in rotating reference frames. Found. Phys. 7, 49 (1982)
R.Y. Chiao, New directions for gravitational-wave physics via ‘Millikan oil drops’, in Visions of Discovery, ed. by R.Y. Chiao, M.L. Cohen, A.J. Leggett, W.D. Phillips, C.L. Harper Jr. (Cambridge University Press, London, 2011), p. 348
J.C. Garrison, R.Y. Chiao, Quantum Optics (Oxford University Press, Oxford, 2008). Equation (2.103)
J.C. Garrison, R.Y. Chiao, Quantum Optics (Oxford University Press, Oxford, 2008). Equation (15.30)
M. Aspelmeyer, P. Meystre, K. Schwab, Quantum optomechanics. Phys. Today 65, 29 (2012)
S. Kuhr, S. Gleyzes, C. Guerlin, J. Bernu, U.B. Hoff, S. Deléglise, S. Osnaghi, M. Brune, J.M. Raimond, S. Haroche, E. Jacques, P. Bosland, B. Visentin, Ultrahigh finesse Fabry-Perot superconducting resonator. Appl. Phys. Lett. 90, 164101 (2007)
R.W. Boyd, Nonlinear Optics (Academic Press, San Diego, 2003)
R.Y. Chiao, L.A. Martinez, S.J. Minter, A. Trubarov, Parametric oscillation of a moving mirror driven by radiation pressure in a superconducting Fabry–Perot resonator system. Phys. Scr. T 151, 014073 (2012). ar**v:1207.6885
M. Philipp, P. von Brentano, G. Pascovici, A. Richter, Frequency and width crossing of two interacting resonances in a microwave cavity. Phys. Rev. E 62, 1922 (2000)
I.G. Wilson, C.W. Schramm, J.P. Kinzer, High Q resonant cavities for microwave testing. Bell Syst. Tech. J. 25(3), 408–434 (1946)
D.J. Griffiths, Introduction to Electrodynamics, 3rd edn. (Prentice Hall, New York, 1999), p. 351
J.D. Jackson, Classical Electrodynamics, 3rd edn. (Wiley, New York, 1998), p. 261
V.B. Braginsky, S.E. Strigin, S.P. Vyatchanin, Parametric oscillatory instability in Fabry-Perot interferometer. Phys. Lett. A 287, 331 (2001)
R.Y. Chiao, Analysis and estimation of the threshold for a microwave ‘pellicle mirror’ parametric oscillator, via energy conservation. ar**v:1211.3519
J.C. Garrison, R.Y. Chiao, Quantum Optics (Oxford University Press, Oxford, 2008), p. 89
P.D. Nation, J.R. Johansson, M.P. Blencowe, F. Nori, Colloquium: stimulating uncertainty: amplifying the quantum vacuum with superconducting circuits. Rev. Mod. Phys. 84, 1 (2012)
S.J. Minter, K. Wegter-McNelly, R.Y. Chiao, Do mirrors for gravitational waves exist? Physica E 42, 234 (2010). ar**v:0903.0661
C.N. Yang, Concept of off-diagonal long-range order and the quantum phases of liquid He and of superconductors. Rev. Mod. Phys. 34, 694 (1962)
C.W. Misner, K.S. Thorne, J.A. Wheeler, Gravitation (Freeman, San Francisco, 1972)
Acknowledgements
D.A.S. acknowledges the support of a 2012–2013 Fulbright Senior Scholar Grant. We thank Jay Shar** for his help in our experiments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2014 Springer-Verlag Italia
About this paper
Cite this paper
Chiao, R.Y. et al. (2014). A Gravitational Aharonov-Bohm Effect, and Its Connection to Parametric Oscillators and Gravitational Radiation. In: Struppa, D., Tollaksen, J. (eds) Quantum Theory: A Two-Time Success Story. Springer, Milano. https://doi.org/10.1007/978-88-470-5217-8_14
Download citation
DOI: https://doi.org/10.1007/978-88-470-5217-8_14
Publisher Name: Springer, Milano
Print ISBN: 978-88-470-5216-1
Online ISBN: 978-88-470-5217-8
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)