Fast Interpolating BMC

Abstract

Bounded Model Checking (BMC) is well known for its simplicity and ability to find counterexamples. It is based on the idea of symbolically representing counterexamples in a transition system and then using a SAT solver to check for their existence or their absence. State-of-the-art BMC algorithms combine a direct translation to SAT with circuit-aware simplifications and work incrementally, sharing information between different bounds. While BMC is incomplete (it can only show existence of counterexamples), it is a major building block of several complete interpolation-based model checking algorithms. However, traditional interpolation is incompatible with optimized BMC. Hence, these algorithms rely on simple BMC engines that significantly hinder their performance. In this paper, we present a Fast Interpolating BMC (Fib) that combines state-of-the-art BMC techniques with interpolation. We show how to interpolate in the presence of circuit-aware simplifications and in the context of incremental solving. We evaluate our implementation of Fib in AVY, an interpolating property directed model checker, and show that it has a great positive effect on the overall performance. With the Fib, AVY outperforms ABC implementation of Pdr on both HWMCC’13 and HWMCC’14 benchmarks.

This material is based upon work funded and supported by the Department of Defense under Contract No. FA8721-05-C-0003 with Carnegie Mellon University for the operation of the Software Engineering Institute, a federally funded research and development center. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the United States Department of Defense. This material has been approved for public release and unlimited distribution. DM-0002152.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Bounded Model Checking (BMC) [4, 5] has emerged as an efficient bug-finding model checking algorithm. It is based on an exploration of bounded paths in a transition system with respect to a property. The main idea behind it is to unroll the transition system up to a given bound k. Unrolling is done by duplicating the transition system k times, attaching the k copies together, and creating a formula, called the BMC or the unrolling formula,  representing all paths of length k. The formula is then constrained by the checked property and is passed to a SAT-solver. If the formula is found to be satisfiable, a counterexample of length k exists. Otherwise, the formula is unsatisfiable, thus no counterexample of length k exists.

State-of-the-art BMC engines are able to find a long counterexample or prove properties up to a large bound. We call such engines fast. Their efficiency lies in a variety of optimizations that use advances in SAT-solving, such as incrementality and assumptions [14, 15] as well as circuit-aware simplifications [1]. Circuit-aware simplifications, such as SAT-swee** [21], use high-level structure of the design to simplify the unrolling formula before sending it to the SAT-solver.

While BMC is incomplete, it is the basis of many complete SAT-based model checking algorithms, such as Interpolation-based Model Checking (Imc) [22, 27, 28], and k-induction, and others (e.g., [23, 25]). We focus on the applications of BMC in Imc. Imc engines use a simple, non-optimized, BMC. This is largely due to the complexity of interpolation in the presence of circuit-aware simplifications and incremental SAT. For instance, simplifications destroy the structure of the unrolling formula, making interpolation difficult. Using simple BMC engines significantly hinders the performance of Imc.

In this paper, we present a Fast Interpolating BMC (Fib). Fib combines the state-of-the-art circuit-aware simplifications, incremental solving, and interpolation. The key insight is to apply simplifications in a way that enables to reconstruct the interpolants from the simplified formula to interpolants for the original formula. To deal with incremental SAT, we extend clausal proofs [18] and their interpolation [17] to the incremental setting.

To elaborate, let $F=A(X,Y)\wedge B(Y,Z)$ be an unsatisfiable formula. A Craig interpolant I(Y) is a formula such that $A(X,Y)\rightarrow I(Y)$ and $I(Y)\wedge B(Y,Z)\rightarrow \bot$. An interpolant is dependent on the structure of F and its partitioning into A and B. A simplification procedure is not aware of the interpolation partitioning of F, and, thus, might destroy it, eliminating the ability to interpolate. For example, consider a case where a simplification procedures finds the variables $y_1,y_2\in Y$ to be equivalent. The simplified formula is $F' = F[y_2\leftarrow y_1]$, i.e., $y_2$ is substituted with $y_1$. An interpolant $I'(Y)$ with respect to $F'$ it is not necessarily an interpolant with respect to F since $I'$ does not have the information about $y_1$ being equal to $y_2$. This equality is a consequence of F, but after substitution, it is implicitly embedded in the simplified formula $F'$, and thus lost.

In Fib, we simplify different partitions of the formula separately, explicitly propagating facts between partitions. This compactly logs the simplification steps. Since Fib takes control from the simplifier by managing the generated consequences, it can then use this information to reconstruct the interpolant $I'(Y)$ of the simplified formula $F'$ to an interpolant that matches F.

Furthermore, since interpolation requires a proof-logging SAT-solver, we develop an incremental SAT-solver that logs proofs [18] incrementally. Unlike a regular incremental SAT-solver, a proof-logging solver must efficiently manage the proof and learned clauses. In the incremental setting, the proof grows with each call to the solver. This dramatically increases the memory requirements of the solver. We, therefore, introduce a heuristic to keep the proof as small as possible while maintaining the benefits of an incrementality.

We evaluate Fib on the benchmarks from the Hardware Model Checking Competitions (HWMCC’13 and ’14). We show that the performance of Fib lies between that of a highly optimized (we use &bmc command of ABC [8]) and simple BMC engines. More importantly, to evaluate the impact of Fib in the context of Imc, we have integrated it in Avy  [28], an advanced interpolation-based algorithm that was shown to be on-par with Pdr. We compare Avy+Fib to Avy and to the implementation of Pdr in ABC (pdr command). Our results show that Avy+Fib solves more instances on both HWMCC’13 and HWMCC’14 than either Avy or Pdr. Additionally, when comparing run-time, Avy+Fib is the most efficient. Our experiments show the importance of a fast BMC engine in Imc.

We make the following contributions: (1) we show how to combine interpolation and an optimized BMC engine; (2) we implement our technique in a BMC engine called Fib and evaluate its performance and impact in the context of an advanced interpolation-based model checker Avy; and (3) our implementation is publicly available and can be used by others in future research.

Related Work. There is a large body of work on structure-aware formula simplification and the interaction between simplifications and SAT-solvers (e.g., [1, 6, 13, 24]). However, these works do not deal with proofs or interpolation.

The closest work that deals with proofs, simplifications, and logic synthesis is [9]. Their goal is to certify correctness of combinatorial equivalence checking (CEC). The key insight is that the proof of simplification steps naturally corresponds to extended resolution [26]. While this procedure can be used to construct an extended resolution proof that tracks both simplifications and SAT-solving, interpolation over extended resolution is difficult. For example, the interpolant is worst-case exponential in the size of the proof [7].

Alternatively, advanced SAT-preprocessing can be used to simulate circuit-aware simplifications directly on CNF [20]. For example, Blocked Clauses Elimination (BCE) [19] simulates Cone-Of-Influence (COI) reduction. Recently, a proof format, called DRAT, that can log such preprocessing efficiently, was introduced in [29]. However, since DRAT simulates extended resolution, interpolation is not trivial and the same problem as in [9] arises. In contrast, our approach uses existing simplification and interpolation procedures and guarantees that the interpolants are linear in the size of resolution proofs involved.

2 Preliminaries

In this section we describe the needed background for the reminder of the paper.

Propositional Satisfiability. Given a set U of Boolean variables, a literal $\ell$ is a variable $u\in U$ or its negation. A clause is a disjunction of literals. A propositional formula F in Conjunctive Normal Form (CNF) is a conjunction of clauses. It is often convenient to treat a clause as a set of literals, and a CNF as a set of clauses. For example, given a CNF formula F, a clause c and a literal $\ell$, we write $\ell \in c$ to mean that $\ell$ occurs in c, and $c \in F$ to mean that c occurs in F. A CNF is satisfiable if there exists a satisfying assignment such that every clause in it is evaluated to $\top$. Otherwise, it is unsatisfiable. A SAT-solver is a complete decision procedure that determines whether a given CNF is satisfiable. If the clause set is satisfiable then the SAT solver returns a satisfying assignment for it. Otherwise, if the solver is proof-logging, it produces a proof of unsatisfiability [16, 17, 23, 30]. In this work we use DRUP-proofs [18]. A DRUP-proof $\pi$ is a sequence of all clauses learned and deleted during the execution of the SAT-solver, in the order in which the learning and deletion happen.

We assume that the reader is familiar with the basic interface of an incremental SAT-solver [14]. We use the following API: (a) $\mathtt{Sat\_Add}(\varphi )$ adds clauses corresponding to the formula $\varphi$ to the solver; (b) $\mathtt{Sat\_DB}$ is the set of all currently added clauses; (c) $\mathtt{Sat\_Reset}$ resets the solver to the initial state; (d) $\mathtt{To\_Cnf} (F)$ converts a formula F to CNF; (e) $\mathtt{Sat\_Solve} (A)$ returns true if $\mathtt{Sat\_DB}$ is satisfiable; Note that $\mathtt{Sat\_Solve} (A)$ optionally takes a set of literals A, called assumptions. If A is not empty, then $\mathtt{Sat\_Solve} (A)$ determines whether A and $\mathtt{Sat\_DB}$ are satisfiable together. We also use $\mathtt{Is\_Sat} (\varphi )$ for deciding whether $\varphi$ is satisfiable, and $\mathtt{Sat\_Mus} (F)$ for a Minimal Unsatisfiable Subset (MUS) [11] of a CNF F. The MUS is computed relative to the clauses already added to the solver.

Modeling Hardware Circuits. A hardware circuit can be described by a propositional formula where state variables (registers), and primary inputs are represented by Boolean variables V and Z, respectively, and the logical operators correspond to the gates. Let $V'$ be a set of primed Boolean variables representing a successor value of state variables V. For each variable $v \in V$, let $f_v(V, Z)$ be the next-state function (NSF) of v. The operation of the circuit is captured by a transition relation $Tr (V,Z,V') \equiv \bigwedge _{v'\in V'} v' = f_v(V,Z)$.

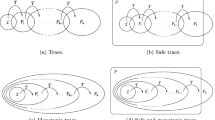
For example, a counter circuit shown in Fig. 1(a) can be modeled by a transition system $Tr (\{v_0,v_1,v_2\},\emptyset ,\{v'_0,v'_1,v'_3\})$ defined as a conjunction of the following NSFs:

$$\begin{aligned} v'_0&= \lnot v_0&v'_1&= v_0 \ne v_1&v'_2&= v_2 \end{aligned}$$

A state s is an assignment to the state variables V. It can be represented as a conjunction of literals that is satisfied in s. More generally, a formula over V represents the set of states that satisfy it. A transition system is a tuple $T=\langle V, Z, Init , Tr , P\rangle$, where the formulas $Init (V)$ and P(V) over V represent the set of initial states and safe states of a circuit, respectively. We call $\lnot P(V)$ the set of bad states. For simplicity, we assume that $Init (V) = \bigwedge _{v\in V} \lnot v$ and P(V) is a literal. $Tr (V,Z,V')$ is a transition relation associating a state s to its successor state $s'$ under a given assignment of the inputs Z. For simplicity, we often omit the primary inputs Z from the transition relation, and omit V and Z from the signature of the transition system when they are clear from the context. We write $V^i$ is to denote the variables in V after i steps of the transition relation. Thus, $V^0 \equiv V$ and $V^1\equiv V'$.

Every propositional formula can be represented by a combinational circuit or a graph. One such representation is And Inverted Graph (AIG) [3]. A formula $\varphi (X)$ over a set of variables X corresponds to a circuit with a set of inputs X, internal nodes corresponding to logical operators, and an output $O_{\varphi }$ that is set to 1 for all assignments to the input X that satisfy $\varphi$. Note that a circuit with multiple outputs represents multiple, independent, propositional formulas – one per output.

Bounded Model Checking. A transition system T is unsafe iff there exists a path from the initial state in $Init$ to a bad state in $\lnot P$ that satisfies the transition relation. This path is called a counterexample. T is unsafe iff there exists a number k such that the following k-unrolling formula is satisfiable:

$$\begin{aligned} Init (V^0) \wedge \left( \bigwedge _{i=0}^{k-1} Tr (V^i, V^{i+1}) \right) \wedge \lnot P(V^k) \end{aligned}$$

(1)

It is useful to view (1) as a combinatorial circuit with inputs $V^0$ and a single output representing the value of $\lnot P(V^k)$. For example, a circuit corresponding to two unrollings of the counter in Fig. 1(a) is shown in Fig. 1(b). Each step of the unrolling (indicated by dashed lines in the figure) is called a frame.

Fig. 1.

A counter and its unrolling.

Fig. 2.

A Simple BMC.

SAT-based Bounded Model Checking (BMC) [5] determines whether a transition system is unsafe by deciding satisfiability of the unrolling formula (1) for increasing values of k. A simple BMC algorithm in shown in Fig. 2.

In practice, fast state-of-the-art BMC implementations combine the simple reduction of BMC to SAT with circuit-aware simplifications of the unrolling formula. Furthermore, they use an incremental SAT interface to share learned clauses between checks for different values of k. To give a general account of circuit aware simplifications, we abstract them using a function

$$\begin{aligned} G'(X,Y),E'(Y) = \mathtt{Simplify} (G(X,Y),E(X)) \end{aligned}$$

(2)

that takes a formula G(X, Y) and a set of input constraints E over X and returns a simplified formula $G'(X,Y)$ and a set of output constraints $E'(Y)$ such that:

$$\begin{aligned} E(X) \rightarrow (G'(X,Y) \equiv G(X,Y)) \qquad (E(X)\wedge G(X,Y)) \rightarrow E'(Y) \end{aligned}$$

(3)

The form of admissible constraints in E depends on the simplification. For example, constant propagation (CP) or ternary simulation requires that E(X) is of the form $\bigwedge _i x_i = c_i$, where $x_i \in X$ and $c_i \in \{0, 1\}$. The output constraints $E'(Y)$ for CP are also of the same form. Another, more general simplification, is SAT-swee** [21] which, restricts the constraints to be equalities between inputs. For our purposes, the inner workings of the simplifications are not important, and we refer an interested reader to ample literature on this subject.

A pseudo-code of a fast BMC is shown in Fig. 3. Unlike simple BMC (Fig. 2), it first constructs a complete unrolling (line 2), then applies circuit-aware simplifications (line 3), and enters the main loop. In each iteration of the loop, it uses a function $\mathtt{Get\_Coi}$ to find the cone-of-influence of the output at depth k (line 5), adds the clauses corresponding to the cone to the solver (line 6, and checks whether the current set of clauses is unsatisfiable together with assumption $\lnot P(V^k)$ (line 7). For simplicity, we assume that conversion to CNF is deterministic and that $\mathtt{Sat\_Add}$ silently ignores clauses that are already known to the solver. A fast BMC is significantly faster than simple BMC and can get much deeper into the circuit.

Fig. 3.

Fast BMC.

Craig interpolation. Given a pair of inconsistent formulas (A, B) (i.e., $A\wedge B\, \models \bot$), a Craig interpolant [10] for (A, B) is a formula I such that:

$$\begin{aligned} A&\rightarrow I&I&\rightarrow \lnot B&\mathcal {L}(I)&\subseteq \mathcal {L}(A) \cap \mathcal {L}(B) \end{aligned}$$

(4)

where $\mathcal {L}(A)$ denotes the set of all variables in A. A sequence (or path) interpolant extends interpolation to a sequence of formulas. We write ${\varvec{F}}= [F_1, \ldots , F_N]$ to denote a sequence with N elements, and $F_i$ for the ith element of the sequence. Given an unsatisfiable sequence of formulas ${\varvec{A}}=[A_1,\ldots ,A_N]$, (i.e., $A_1\wedge \cdots \wedge A_N \models \bot$) a sequence interpolant ${\varvec{I}}= \textsc {seqItp}({\varvec{A}})$ for ${\varvec{A}}$ is a sequence of formulas ${\varvec{I}}= [I_1,\ldots ,I_{N-1}]$ such that:

$$\begin{aligned} A_1&\rightarrow I_1&\forall 1 < i < N \cdot I_{i-1} \wedge A_i&\rightarrow I_i&I_{N-1} \wedge A_N&\rightarrow \bot \end{aligned}$$

(5)

and for all $1 \le i \le N$, $\mathcal {L}(I_i) \subseteq \mathcal {L}(A_1 \wedge \cdots \wedge A_i) \cap \mathcal {L}(A_{i+1} \wedge \cdots \wedge A_N)$.

3 Simplification-Aware Interpolation

We begin with an illustration of the difficulties of interpolation in the presence of circuit-aware simplifications. Consider the counter circuit and its unrolling G shown in Fig. 1. Recall, initially all registers are zero. Assume that we want an interpolant between the first and second frames $G_0$ and $G_1$, respectively, where $G = G_0 \wedge G_1$, under the assumption $\lnot P^2 = \lnot (v_0^2 \wedge v_1^2 \wedge v_2^2)$. Simplifying G using constant propagation, which replaces outputs of gates with constants based on the values of its inputs, reduces it to $v_0^2=0 \wedge v_1^2=1 \wedge v_2^2=0$ that is trivially unsatisfiable together with $\lnot P^2$. However, the simplification destroys the partitioning structure of G, making interpolation meaningless. Alternatively, assume that the simplification does not eliminate intermediate values of the registers. Then, the simplification might reduce G to $G' = G'_0 \wedge G'_1$, where

$$\begin{aligned} G'_0&\equiv v_0^1 = 1 \wedge v_1^1=0 \wedge v_2^1 = 0&G'_1&\equiv v_0^2=0 \wedge v_1^2=1 \wedge v_2^2=0 \end{aligned}$$

While the partitioning structure is preserved, not every interpolant of $(G'_0, G'_1 \wedge \lnot P^2)$ is an interpolant of $(G_0, G_1\wedge \lnot P^2)$. For example, $\top$ is an interpolant in the first case, but not in the second. Such problems are even more severe for more complicated simplifications such as SAT-swee**, in which case additionally variables that are local to a partition before the simplification might become shared between partitions after.

The source of the problems is that the reasoning done by the simplification is hidden from the interpolation procedure. One way to expose it is to use proof-logging simplifications. Let G be a circuit, and $G'$ a simplified version of G such that $G \rightarrow G'$ and $G' \rightarrow \bot$. Then, there exists a resolution proof $\pi _1$ of $G \rightarrow G'$ and a resolution proof $\pi _2$ of $G' \rightarrow \bot$. If we require a simplification to produce $\pi _1$ while constructing $G'$, and require a SAT-solver to produce $\pi _2$ while deciding satisfiability of $G'$, then, we can construct a complete resolution proof $\pi = \pi _1\mathop {;}\pi _2$ of $G \rightarrow \bot$ and apply interpolation to $\pi$. In fact, this approach is used in [17] for interpolation in the presence of SAT pre-processing [12].

While there are suggestions in literature (e.g., [9]) on how to extract resolution proofs out of circuit-aware simplifications, this is non-trivial. It requires significant changes to existing simplifiers, and is particularly difficult for simplifications that are done as a by-product of using efficient data-structures such as AIGs and BDDs. Furthermore, as shown in [9], circuit-aware simplifications correspond naturally to extended resolution proofs. However, interpolation over extended resolution is difficult, and the interpolants are worst-case exponential in the size of the proof. Furthermore, the proof logging is likely to incur a non-trivial overhead and is likely to be much more detailed than necessary for interpolation in our target applications.

In this section, we suggest an alternative light-weight approach. Instead of applying the simplifications to the complete unrolling, we apply them to each individual frame (or partition), and propagate constraints between frames. Instead of requiring simplifications to be proof-logging, we log the constraints that are exchanged. In our setting, simplifications preserve the partitioning of the original formula. We show how to use the logged constraints to reconstruct a sequence interpolant of the simplified formula to a sequence interpolant of the original formula. Finally, we propose a minimization algorithm to ensure that the final interpolant does not contain redundant constraints.

Constraint-Logging Simplifications. Let $G = G_0(V^0, V^1) \wedge \cdots \wedge G_k(V^k, V^{k+1})$ be a formula divided into k partitions. Note that variables are shared between two adjacent partitions only. Our constraint-logging simplification algorithm $\mathtt{Loc\_Simp}$ is shown in Fig. 4. It processes the formula G left-to-right. In each step, it simplifies $G_i$ using constraints $E_i$ of the prefix, and generates new consequences $E_{i+1}$ to be used by the next step. For example, if G is an unrolling formula, then $E_i$ is a set of consequences that are implied by the states reachable in $(i+1)$ states from the initial state. Note that in this case, the initial state is embedded in $G_0$.

Fig. 4.

Localized simplification ($\mathtt{Loc\_Simp} (G)$).

Let $G' = G'_0 \wedge \cdots \wedge G'_k$ be a formula obtained by $\mathtt{Loc\_Simp} (G)$ and $E_1, \ldots , E_{k+1}$ be the corresponding trail of constraints. Assume that $G'$ is unsatisfiable, and let ${\varvec{I}}= \langle I_1, \ldots , I_k \rangle$ be a sequence interpolant of $G'$. Recall that ${\varvec{I}}$ is an interpolant w.r.t. the simplified formula $G'$ and, therefore, may not be an interpolant w.r.t. the original formula G. The reason is that some of the consequences that were generated by the simplification are present implicitly in the simplified formula and, thus, are missing from the interpolant. This requires a post-processing step that adds the missing information to the sequence-interpolant.

Theorem 1

Let $G = G_0(V^0, V^1) \wedge \cdots \wedge G_k(V^k, V^{k+1})$ be a formula partitioned into k parts, and let $(G'=G'_0 \wedge \cdots \wedge G'_k,\langle E_1,\ldots ,E_{k+1}\rangle )$ be the result of $\mathtt{Loc\_Simp} (G)$. If $G'$ is unsatisfiable and $\langle I'_1,\ldots ,I'_k\rangle$ is a sequence-interpolant of $G'$ then

• G is unsatisfiable, and

• $\langle I'_1\wedge E_1,\ldots ,I'_k\wedge E_k\rangle$ is a sequence-interpolant of G.

Proof

Since $\langle I'_1,\ldots ,I'_k\rangle$ is a sequence-interpolant of $G'$ we know that:

$$\begin{aligned} G'_0&\rightarrow I'_1&\forall 1 \le i < k \cdot (I'_i \wedge G'_i)&\rightarrow I'_{i+1}&I'_{k} \wedge G'_k&\rightarrow \bot \end{aligned}$$

(6)

By construction, the trail $\langle E_0, \ldots , E_{k+1} \rangle$ satisfies:

$$\begin{aligned} G_0&\rightarrow E_1&\forall 1 \le i \le k \cdot (E_i \wedge G_i)&\rightarrow E_{i+1} \end{aligned}$$

(7)

Finally, by the properties of $\mathtt{Simplify}$, we have:

$$\begin{aligned} G_0&\rightarrow G'_0&\forall 1 \le i < k \cdot (E_i \wedge G_i)&\rightarrow G'_i \end{aligned}$$

(8)

Combining the above together, we get:

$$\begin{aligned} G_0&\rightarrow I'_1\wedge E_1&\forall 1 \le i < k \cdot (I'_{i}\wedge E_{i} \wedge G_{i})&\rightarrow (I'_{i+1} \wedge E_{i+1})&I'_{k}\wedge E_k \wedge G'_k&\rightarrow \bot \end{aligned}$$

(9)

Theorem 1 gives a simple way to reconstruct a sequence-interpolant of the simplified formula to the original formula. However, the resulting interpolant is likely not to be minimal. Each $E_i$ may contain many constraints that are not necessary for the validity of the sequence-interpolant. Thus, we propose an algorithm to minimize sequence interpolants. First, we formally define what we mean by minimality.

Definition 1

Let $\bar{{\varvec{I}}}= \langle I_1,\ldots ,I_k\rangle$ be a sequence-interpolant where each element $I_i$ is a conjunction (or a set) of constraints. The sequence $\bar{{\varvec{I}}}$ is minimal if any other sequence obtained by removing at least one constraint from any of the $I_i$ is not a sequence-interpolant.

Our algorithm, $\mathtt {Min\_Itp}$, is shown in Fig. 5. It takes a partitioned formula G and a sequence interpolant ${\varvec{I}}$ as input, and returns a minimal sequence interpolant ${\varvec{I}}'$. It applies an iterative backward search for the necessary constraints from $I_k$ to $I_1$. In each iteration, it computes the needed constraints $I'_i\subseteq I_i$ that ensures that $I'_i \wedge G_i \rightarrow I'_{i+1}$. This is accomplished by asserting $G_i \wedge \lnot I'_{i+1}$ and computing an MUS of $I_i$ relative to those background constraints. The soundness of $\mathtt {Min\_Itp}$ follows from the loop invariant described above. The minimality follows from the minimality of the MUS computation.

Lemma 1

Let $G = G_0(V^0, V^1) \wedge \cdots \wedge G_k(V^k, V^{k+1})$ be an unsatisfiable formula partitioned into k parts, and ${\varvec{I}}$ be its sequence interpolant. Then, ${\varvec{I}}' = \mathtt {Min\_Itp}(G, {\varvec{I}})$ is a minimal sequence interpolant for G.

Fig. 5.

Minimal sequence-interpolant $\mathtt {Min\_Itp}(G, {\varvec{I}})$.

Recall that in the traditional interpolation techniques the size of the interpolant is linear in the size of the resolution proof. In the presence of the simplifications, the size of the interpolant is linear in the size of the resolution proof of the simplified formula and the number of constraints introduced by the simplification, whichever is greater. Let $F=A(X,Y)\wedge B(Y,Z)$ be an unsatisfiable formula and $F'=A'(X,Y)\wedge B'(Y,Z)$ be a simplified formula, where $(A',E) = \mathtt{Simplify} (A,\emptyset )$, and $B'=\mathtt{Simplify} (B,E)$. An interpolant $I'$, computed with respect to $F'$, is linear in the size of the resolution proof for $F'$. Let the size of E be bounded by $\psi (A)$ (i.e. $|E|\le \psi (A)$), and let $I = I' \wedge E$ be the interpolant constructed by our method. Since I is generated by adding constraints from E to $I'$, its size is bounded by $\max \{|I'|,\psi (A)\}$. Interestingly, for common simplifications like CP and SAT-swee**, $\psi (A)=|Y|$, it can only generate as many consequences as the number of interface variables. Thus, in this case the size of interpolant is bounded by the number of shared variables or the size of the simplified proof, whichever is greater.

Fast Interpolating BMC. Using the machinery of simplification-aware interpolation, we now present our fast interpolating BMC (Fib) algorithm. The pseudo-code of Fib is shown in Fig. 6. Structurally, it is similar to the fast BMC shown in Fig. 3. The first difference is that the unrolling formula G is partitioned into frames $G_i$. Second, instead of simplifying the unrolling, we use $\mathtt{Loc\_Simp}$ to simplify each frame and collect the trail of side-constraints. Then, in each iteration of the main loop, the cone of influence of the current $\lnot P(V^k)$ is computed and added to the SAT-solver. If the result is UNSAT, Fib computes an interpolant of the current simplified k-unrolling, extends it with the side-conditions, and minimizes using $\mathtt {Min\_Itp}$. The result is made available to the user using a call to $\mathtt{yield}$. Thus, in addition to detecting counterexamples, Fib computes a trail of sequence interpolants. One sequence for each safe bound.

Note that we assume that it is possible to compute interpolants (see the call to ${tt Sat\_Itp}$) in an incremental SAT-solver. That is, we expect interpolants to be available after the SAT-solver is called with assumptions, and during repeated calls to $\mathtt{Sat\_Solve}$ with new clauses added in between. While in theory supporting interpolation in an incremental SAT-solver is straight-forward, it is difficult to do efficiently in practice. We address this issue in the next section.

Fig. 6.

Fast Interpolating BMC (Fib).

4 Interpolating Incremental SAT Solver

In this section, we describe our implementation of an interpolating incremental solver that supports both an incremental addition of clauses and solving with assumptions. The keys to our approach are DRUP [18] and DRUP-interpolation [17].

DRUP proofs were introduced in [18] in the context of SAT-solver certification. Since we use them for interpolation, we begin by reviewing DRUP-proofs and interpolation as they appear in [17]. Let F be an unsatisfiable propositional formula in CNF. A DRUP-proof $\pi$ is a sequence of all clauses learned and deleted during the execution of the SAT-solver, in the order in which the learning and deletion happen. Meaning, the first clause in $\pi$ is the first learned clause, and the last clause is the empty clause. Let $\pi =\langle c_0,\ldots , c_n\rangle$ be a DRUP-proof, then a non-deleted clause $c_i$ is derivable by trivial resolution [2] from F and from all non-deleted clauses $c_j$ for $0\le j < i$. The interpolation procedure in [17] labels each clause in $c_i\in \pi$ with a sequence of propositional formule $\bar{I}(c_i)$, where the label of the last clause, i.e. $\bar{I}(c_n)$, is the sequence-interpolant.

Fib uses the SAT-solver incrementally in two ways: (1) the solver is called with assumptions, and (2) new clauses are added. The two steps are iterated repeatedly. Because of multiple calls, the learned clauses that are currently part of the SAT-solver’s database are being used in a consecutive calls to the solver.

We first address the problem of interpolation under assumptions. In the presence of assumptions, the final learned clause produced by the solver, provided that the instance is unsatisfiable, is not the empty clause, but a clause containing negated assumption literals. We claim that whenever the assumptions are local to each interpolation-partition the formula that marks the final clause is the sequence-interpolant.

Proposition 1

Let $F=F_1(X_1,Y_1,X_2)\wedge \cdots \wedge F_k(X_k,Y_k,X_{k+1})$ be a propositional formula in CNF. Assume that F is unsatisfiable under assumptions $\{a_1,\ldots ,a_k\}$. Let $\pi =\{c_0,\ldots ,c_n\}$ be a corresponding DRUP-proof. If for all $1\le i\le k$, $a_i\in Y_i$, then a $\bar{I}(c_n)$ is a sequence-interpolant of $\bigwedge _{i=1}^k (F_i\wedge a_i)$.

Incremental addition of new clauses and multiple calls to $\mathtt{Sat\_Solve}$ create new challenges to a proof-logging SAT solver. First, the solver must ensure that the DRUP-proof remains consistent. More precisely, every learned clause in a DRUP-proof must be derivable by trivial resolution [2] using original clauses and learned clauses that were part of $\mathtt{Sat\_DB}$ when it was learned. This is tricky in an incremental setting because original clauses might be added after learned clauses. For example, assume that initially $\mathtt{Sat\_DB}$ contained the set of original clauses $F_1$ and after some time the DRUP-proof is a sequence of two clauses $(c_1, c_2)$. Then, by the DRUP property, $c_2$ follows from $F_1 \wedge c_1$ by trivial resolution. Next, assume that additional original clauses $F_2$ were added to the solver via $\mathtt{Sat\_Add}$. After some time, the DRUP-proof might be $(c_1, c_2, c_3)$. At this point, the fact that $c_2$ is derivable only from $F_1$ and $c_1$ is lost. This makes it difficult to reconstruct (or even approximate) the original resolution proof produced by the SAT-solver to derive $c_2$. While this might be an issue if the goal is to validate the solver, it is not in our case. The database of clauses $\mathtt{Sat\_DB}$ is growing monotonically. Thus, if a clause was derivable by a trivial resolution at one point, it remains derivable if new clauses are added to the database. Hence, in our implementation, we disregard the order in which the original clauses are added to the database. Thus, the proof that is found during interpolation might be significantly different from the original proof used implicitly by the SAT-solver.

Another challenge is memory requirement. In an incremental solver, learned clauses are re-used between the calls to $\mathtt{Sat\_Solve}$ and the number of learned clauses grows monotonically. This is not an issue for non-interpolating solvers since they prune learned clauses even in a non-incremental mode. However, an interpolating solver that logs the DRUP-proof must keep all clauses ever learned in memory because even though a clause is deleted at one time, it might have participated in the proof at prior time. To address this, we use the following heuristic. Recall that DRUP-interpolation first finds the core clauses and then traverses them, rebuilding the proof and generating the interpolant. We change it to also mark as core the unit clauses that are on the trail during the last conflict. The intuition is that units are very strong consequences and are likely to be useful in other $\mathtt{Sat\_Solve}$ calls. Finally, between every call to $\mathtt{Sat\_Solve}$, we prune the DRUP proof and the learned clauses from all non-core clauses. Thus, the only learned clauses that remain between $\mathtt{Sat\_Solve}$ calls are clauses that appear in the last resolution proof, units on the trail, and clauses that are necessary to derive the units from $\mathtt{Sat\_DB}$.

5 Experiments

We have implemented Fib inside our model checking framework Avy ¹. We evaluate our implementation of Fib in two ways. First, we evaluate Fib as a BMC engine by comparing it with both a simple BMC and a fast BMC (&bmc) of ABC [8]. Second, we integrate Fib in Avy, an Interpolation-based Model Checker, and show the impact it has on performance, both in run-time and the number of solved instances. We use all of HWMCC’13 and ’14 benchmarks, an Intel Xeon 2.4GHz processor with 128GB of memory, and a timeout of 900 s.

BMC Evaluation. We compare Fib to a simple BMC implementation, and then to a fast BMC of ABC. We expect Fib to perform in between the fast and simple BMCs. Figure 7 shows a comparison of runtime when running all the different BMC algorithms until depth 40 on the benchmarks in which at least one tool ran to completion. That is, at least one tool either finds a counterexample or proves no counterexamples of depth up to 40. As expected, Fib is more efficient than a simple BMC on most cases and ABC BMC is more efficient than Fib. Some of the difference are due to the way simplification is applied in Fib. We believe that with a more careful implementation this gap can be closed.

Fig. 7.

Runtime comparison between Fib, ABC’s BMC (&bmc) and Simple BMC. Points above the line are in favor of Fib. Square represents a timeout.

Fig. 8.

Depth comparison between Fib, ABC’s BMC and Simple BMC. Triangles are cases solved to completion by at least one tool. Points below the line are in favor of Fib. Triangle represents timeout.

Figure 8 shows a comparison of the depth reached during an execution of the algorithms for bound 40 in the presence of a predefined time limit. Clearly, Fib reaches deeper bounds compared to the simple BMC engine. Compared to ABC BMC, Fib is mostly on par with a few cases in favor of ABC. Note that the problem is exponential in the depth, so even a small increase is significant.

On a few test cases, we have noticed that Fib performs worse than a simple BMC engine. Analyzing those cases revealed that sometime the simplified formula, even though having less clauses and less variables, is harder for the SAT-solver. While this is not a common case, it may happen. Our intuition is that this is most likely due to the solver spending more time in a harder part of the search space.

Model Checking Evaluation. For these sets of experiments, we have integrated Fib in Avy and called it Avy+Fib. We compared Avy+Fib with the original Avy and with ABC implementation of Pdr (pdr). Table 1 summarizes the number of solved instances by each algorithm and total runtime on the entire benchmark. Avy+Fib solves the most cases in both HWMCC’13 and HWMCC’14. On HWMCC’13 it solves 5 more cases than Avy and 32 more cases than Pdr, and it cannot solve 4 cases solved by Avy and 12 cases solved by Pdr. On HWMCC’14 it solves 8 more than Avy and 26 more than Pdr, and it cannot solve 1 case solved by Avy and 7 cases solved by Pdr.

Table 1. Summary of solved instances on HWMCC’13 and HWMCC’14.

Table 1 also shows two Virtual Best (VBS) results. The first corresponds to combining Avy+Fib and Pdr, the second to combining Avy and Pdr. As expected, the addition of Avy+Fib to Pdr is the better option.

As we describe in Sect. 3, during the computation of an interpolant, the set of constraints generated by the simplifier is minimized. We measured the time minimization takes. The median value are 5.6 s and 4.78 s for HWMCC’13 and ’14, respectively. This shows that in most cases this process is efficient.

Even though Avy+Fib uses a faster BMC engine than Avy, there are still cases solved by Avy and not by Avy+Fib. Analyzing those showed that sometimes simplification creates “noise” and forces a proof that is very dependent on the initial state. Since Fib propagates the initial values as far as it can, it might also increase the convergence bound of Avy. This behavior may hurt performance, yet we rarely observe it in practice. Moreover, in some cases, even when the convergence bound is increased, Avy+Fib is still faster than Avy.

Fig. 9.

Runtime comparison of Avy+Fib, Avy+BMC and Pdr on HWMCC’13 (green) and HWMCC’14 (blue) benchmarks. Rhombus represents a timeout.

Considering total runtime, Avy+Fib is more efficient than both Avy and Pdr. Figure 9 shows run-time comparison per test case for each HWMCC’13 and ’14. Analyzing individual runtimes shows that Avy+Fib (just like Avy) is very different from Pdr. Each of them performs better than the other on a different class of benchmarks. This is evident in Fig. 9(a) where most of the points are on the extremes (axis) of the plots. Figure 9(b) shows that Avy+Fib is more efficient than Avy on most of the benchmarks. We also analyzed the median value w.r.t. runtime on solved instances. Avy’s median values on HWMCC’13 and ’14 are 94.2 and 35.9, respectively. While for Avy+Fib, the values are 53.4 and 23.4 respectively.

6 Discussion and Conclusions

The paper presents a novel method for interpolation over BMC formulas when circuit-aware simplifications are applied. Our approach is based on the observation that for the purpose of interpolation, only the consequences generated by the simplifier need to be logged. These consequences can then be used to reconstruct an interpolant w.r.t. to the original formula from an interpolant computed w.r.t. the simplified formula. This approach is simpler than trying to reconstruct the proof itself.

We implemented our approach in an engine called Fib and evaluated its impact on model checking by incorporating it into Avy. The experimental results show that Fib improves the performance of Avy significantly.

Fib puts some restrictions on the way the simplifier operates. This can be seen in the gap between Fib and ABC’s BMC engine. We believe that most of these restrictions can be removed and that interpolation is possible even when using an unrestricted simplifier. Enabling this may further close the gap between Fib and state-of-the-art BMC engines. We leave this challenge for future research.