Bifurcation mechanism and hybrid control strategy of a finance model with delays

Abstract

Establishing financial models or economic models to describe economic phenomena in real life has become a heated discussion in society at present. From a mathematical point of view, the exploration on dynamics of financial models or economic models is a valuable work. In this study, we build a new delayed finance model and explore the dynamical behavior containing existence and uniqueness, boundedness of solution, Hopf bifurcation, and Hopf bifurcation control of the considered delayed finance model. By virtue of fixed point theorem, we prove the existence and uniqueness of the solution to the considered delayed finance model. Applying a suitable function, we obtain the boundedness of the solutions for the considered delayed finance model. Taking advantage of the stability criterion and bifurcation argument of delayed differential equation, we establish a delay-independent condition ensuring the stability and generation of Hopf bifurcation of the involved delayed finance model. Exploiting hybrid controller including state feedback and parameter perturbation, we efficaciously adjust the stability region and the time of occurrence of Hopf bifurcation of the involved delayed finance model. The study manifests that time delay is a fundamental parameter in controlling stability region and the time of onset of Hopf bifurcation of the involved delayed finance model. To examine the soundness of established key results, computer simulation figures are concretely displayed. The derived conclusions of this study are perfectly new and has momentous theoretical value in economical operation.

1 Introduction

Economic activity is kind of complex behavior of human beings. In many cases, economic activity displays lots of indeterminacies in our life [1]. In mathematics, nonlinear differential equation is a suitable tool to describe this complex phenomenon in economic activity. Thus setting up differential dynamical models to reflect the relationship among variables of economic activity has become a very main task. During the past decades, there are many preeminent works on finance models. For example, Ma and Chen [2, 3] investigated the bifurcation problem and the complicated global behavior of the following finance model.

$$\begin{aligned}& \textstyle\begin{cases} \dot{u}_{1}(t)=u_{3}(t)+(u_{2}(t)-\alpha)u_{1}(t), \\ \dot{u}_{2}(t)=1-\beta u_{2}(t)-u_{1}^{2}(t), \\ \dot{u}_{3}(t)=-u_{1}(t)-\gamma u_{3}(t), \end{cases}\displaystyle \end{aligned}$$

(1)

where $u_{1}(t)$ stands for the interest rate at time t, $u_{2}(t)$ stands for the investment demand at time t, and $u_{3}(t)$ stands for the price index at time t. α represents the savings amount, β represents the cost per investment, γ represents the elasticity of demand of commercial market. α, β, γ are all positive constants. In 2012, Ma and Wang [4] studied the onset of both Hopf bifurcation and topological horseshoe of model (1). In 2009, Gao and Ma [5] dealt with the chaos phenomenon and Hopf bifurcation control of model (1). Yusuf et al. [6] explored the existence and uniqueness of the solutions for the fractional-order version of model (1).

Here we point out that in economic activity the change of the interest rate, the investment demand, and the price index not only depend on the current time, but also depend on the past time. For example, in some cases, the change of the interest rate $u_{1}(t)$ is affected by $u_{2}(t)$ and $u_{2}(t-\sigma)$, where σ is a positive constant. Thus time delay often arises in economic activity. Based on this viewpoint, many scholars pay much attention to delayed finance models and have achieved many outstanding achievements. For instance, Zhang and Zhu [7] studied the Hopf bifurcation and chaos of the following finance system with single delay:

$$\begin{aligned}& \textstyle\begin{cases} \dot{u}_{1}(t)=u_{3}(t-\sigma)+(u_{2}(t)-\alpha)u_{1}(t), \\ \dot{u}_{2}(t)=1-\beta u_{2}(t)-u_{1}^{2}(t), \\ \dot{u}_{3}(t)=-u_{1}(t)-\gamma u_{3}(t), \end{cases}\displaystyle \end{aligned}$$

(2)

where σ is a delay. In 2011, Wang et al. [8] explored the single-periodic, multiple-periodic, and chaotic motions of the following fractional-order financial model:

$$\begin{aligned}& \textstyle\begin{cases} D_{t}^{p_{1}}u_{1}(t)=u_{3}(t)+(u_{2}(t-\sigma)- \alpha)u_{1}(t), \\ D_{t}^{p_{2}}u_{2}(u)=1-\beta u_{2}(t)-u_{1}^{2}(t- \sigma), \\ D_{t}^{p_{3}}u_{3}(t)=-u_{1}(t-\sigma)-\gamma u_{3}(t), \end{cases}\displaystyle \end{aligned}$$

(3)

where $p_{1},p_{2},p_{3}\in(0,1]$ are constants. In 2014, Chen et al. [9] discussed the stability of the unique equilibrium and Hopf bifurcations problem of the following delayed finance model:

$$\begin{aligned}& \textstyle\begin{cases} \dot{u}_{1}(t)=u_{3}(t)+(u_{2}(t-\sigma)-\alpha)u_{1}(t), \\ \dot{u}_{2}(t)=1-\beta u_{2}(t)-u_{1}^{2}(t-\sigma), \\ \dot{u}_{3}(t)=-u_{1}(t-\sigma)-\gamma u_{3}(t). \end{cases}\displaystyle \end{aligned}$$

(4)

In this paper, based on the previous publications and considering that the interest rate and the investment demand are affected by the feedback time of the investment demand, we propose the following delayed finance model:

$$\begin{aligned}& \textstyle\begin{cases} \dot{u}_{1}(t)=u_{3}(t)+(u_{2}(t-\sigma)-\alpha)u_{1}(t), \\ \dot{u}_{2}(t)=1-\beta u_{2}(t-\sigma)-u_{1}^{2}(t), \\ \dot{u}_{3}(t)=-u_{1}(t)-\gamma u_{3}(t), \end{cases}\displaystyle \end{aligned}$$

(5)

where σ is a time delay that stands for the feedback time of the investment demand. The model (5) plays a vital role in investment field of financial industry.

Delay-induced Hopf bifurcation is a vital dynamical phenomenon in nonlinear dynamical systems [10–25]. In economics, delay-induced Hopf bifurcation can commendably portray the economic phenomenon. Thus we think that it is very meaningful to study delay-induced Hopf bifurcation of finance models. In addition, to control the stability region and the onset of Hopf bifurcation to serve human beings, in some cases we need to enlarge or narrow the stability region, delay, or advance the time of the onset of Hopf bifurcation of finance models. Stimulated by this viewpoint, we are to explore the Hopf bifurcation and Hop bifurcation control issue of model (5). In particular, we will explore the following topics: (i) Prove the existence, uniqueness, and boundedness of the solution to model (5). (ii) Analyze the stability and Hopf bifurcation of model (5). (iii) Explore Hopf bifurcation control issue of model (5) by utilizing hybrid controller.

The primary highlights of this article are stated as follows: • On the basis of the previous publications, we build a new fractional-order delayed finance model. • The sufficient condition to guarantee the stability and the onset of Hopf bifurcation of model (5) is established. • Taking advantage of hybrid control strategy, the stability region and the time of the onset of Hopf bifurcation of model (5) are effectively controlled. • The influence of delay on the stability and the occurrence of Hopf bifurcation of model (5) has been revealed. • The control idea can be utilized to explore the bifurcation control issue of plenty of differential dynamical models in many fields.

This work is planned as follows: Segment 2 proves the existence and uniqueness, boundedness of the solution of system (5). Segment 3 discusses the stability and the creation of Hopf bifurcation of system (5). Segment 4 explores the Hopf bifurcation control issue of system (5) via a hybrid controller that includes state feedback and parameter perturbation. Segment 5 carries out numerical simulations to verify the correctness of the derived assertions. Segment 6 completes the article.

2 Dynamics analysis on the solution of system (5)

In this part, we will discuss the existence, uniqueness, and boundedness of the solution of system (5) by utilizing fixed-point theorem and a suitable function.

Theorem 1

Denote $\Phi=\{(u_{1},u_{2},u_{3})\in R^{3}: \max\{|u_{1}|,|u_{2}|,|u_{3}| \}\leq{\mathcal{U}}\}$, where ${\mathcal{U}}>0$ represents a constant. For every $(u_{10},u_{20},u_{30})\in\Phi$, system (5) with the initial value $(u_{10},u_{20},u_{30})$ has a unique solution $U=(u_{1},u_{2},u_{3})\in\Phi$.

Proof

We construct a map** as follows:

$$\begin{aligned}& g(U)=\bigl(g_{1}(U), g_{2}(U),g_{3}(U)\bigr), \end{aligned}$$

(6)

where

$$\begin{aligned}& \textstyle\begin{cases} g_{1}(U)=u_{3}(t)+(u_{2}(t-\sigma)-\alpha)u_{1}(t), \\ g_{2}(U)=1-\beta u_{2}(t-\sigma)-u_{1}^{2}(t), \\ g_{3}(U)=-u_{1}(t)-\gamma u_{3}(t). \end{cases}\displaystyle \end{aligned}$$

(7)

For every $U, \tilde{U}\in\Phi$, one derives

$$\begin{aligned}& \bigl\Vert g(U)-g(\tilde{U}) \bigr\Vert \\& \quad = \bigl\vert u_{3}(t)+\bigl(u_{2}(t-\sigma)-\alpha \bigr)u_{1}(t)-\bigl[\tilde{u}_{3}(t)+\bigl( \tilde{u}_{2}(t-\sigma)-\alpha\bigr)\tilde{u}_{1}(t)\bigr] \bigr\vert \\& \qquad {}+ \bigl\vert 1-\beta u_{2}(t-\sigma)-u_{1}^{2}(t)- \bigl[1-\beta\tilde{u}_{2}(t- \sigma)-\tilde{u}_{1}^{2}(t) \bigr] \bigr\vert \\& \qquad {}+ \bigl\vert -u_{1}(t)-\gamma u_{3}(t)-\bigl[- \tilde{u}_{1}(t)-\gamma\tilde{u}_{3}(t)\bigr] \bigr\vert \\& \quad \leq \bigl\vert u_{3}(t)-\tilde{u}_{3}(t) \bigr\vert +\alpha \bigl\vert u_{1}(t)-\tilde{u}_{1}(t) \bigr\vert +{ \mathcal{U}} \bigl\vert u_{2}(t)-\tilde{u}_{2}(t) \bigr\vert \\& \qquad {}+{\mathcal{U}} \bigl\vert u_{1}(t)-\tilde{u}_{1}(t) \bigr\vert +\beta \bigl\vert u_{2}(t)- \tilde{u}_{2}(t) \bigr\vert +2{\mathcal{U}} \bigl\vert u_{1}(t)- \tilde{u}_{1}(t) \bigr\vert \\& \qquad {}+ \bigl\vert u_{1}(t)-\tilde{u}_{1}(t) \bigr\vert +\gamma \bigl\vert u_{3}(t)-\tilde{u}_{3}(t) \bigr\vert \\& \quad =(1+\alpha+3{\mathcal{U}}) \bigl\vert u_{1}(t)- \tilde{u}_{1}(t) \bigr\vert \\& \qquad {}+(\beta+{\mathcal{U}}) \bigl\vert u_{2}(t)- \tilde{u}_{2}(t) \bigr\vert \\& \qquad {}+(1+\gamma) \bigl\vert u_{3}(t)-\tilde{u}_{3}(t) \bigr\vert \\& \quad \leq{\mathcal{A}} \Vert U-\tilde{U} \Vert , \end{aligned}$$

(8)

where

$$\begin{aligned}& {\mathcal{A}}=\max\{1+\alpha+3{\mathcal{U}}, \beta+{\mathcal{U}}, 1+ \gamma\}. \end{aligned}$$

(9)

Then $g(U)$ satisfies Lipschitz condition with respect to U (see [26]). By virtue of fixed-point theorem, we can easily conclude that Theorem 1 is correct. □

Theorem 2

If $2\beta>\alpha$ holds, then all solutions to system (5) beginning with $R_{+}^{3}$ are uniformly bounded.

Proof

Define

$$\begin{aligned}& W(t)=u_{1}^{2}(t)+u_{2}^{2}(t)+u_{3}^{2}(t). \end{aligned}$$

(10)

Then

$$\begin{aligned} \dot{W}(t)+\alpha W(t) =&2\dot{u}_{1}(t)u_{1}(t)+2 \dot{u}_{2}(t)u_{2}(t)+2 \dot{u}_{3}(t)u_{3}(t) \\ &{}+\alpha u_{1}(t)+\alpha u_{2}(t)+\alpha u_{3}(t) \\ =&2u_{1}(t)\bigl[u_{3}(t)+\bigl(u_{2}(t-\sigma)- \alpha\bigr)u_{1}(t)\bigr] \\ &{}+2u_{2}(t)\bigl[1-\beta u_{2}(t-\sigma)-u_{1}^{2}(t) \bigr] \\ &{}+2u_{3}(t)\bigl[-u_{1}(t)-\gamma u_{3}(t) \bigr]+\alpha u_{1}(t)+\alpha u_{2}(t)+ \alpha u_{3}(t) \\ \leq&-\alpha u_{1}^{2}(t)-(2\beta-\alpha)u_{2}^{2}(t)+2u_{2}(t)-(2 \gamma-\alpha) u_{3}^{2}(t) \\ \leq&\frac{1}{2\beta-\alpha}. \end{aligned}$$

(11)

Then

$$ W(t)\rightarrow\frac{1}{\alpha(2\beta-\alpha)},\quad \text{as }t \rightarrow\infty. $$

(12)

The proof of Theorem 2 is completed. □

3 Bifurcation investigation of system (5)

Assume that

$$({\mathcal{C}}_{1})\quad \gamma-\alpha\beta\gamma-\beta>0, $$

then it is easy to derive that system (5) has the following two equilibrium points:

$$U_{1}(u_{1\star},u_{2\star}, u_{3\star}), \qquad U_{2} (-u_{1\star},u_{2 \star}, -u_{3\star} ), $$

where

$$\begin{aligned}& \textstyle\begin{cases} u_{1\star}=\sqrt{ \frac{\gamma-\alpha\beta\gamma-\beta}{\gamma}}, \\ u_{2\star}=\frac{\alpha\gamma+1}{\gamma}, \\ u_{3\star}=-\frac{1}{\gamma}\sqrt{ \frac{\gamma-\alpha\beta\gamma-\beta}{\gamma}}. \end{cases}\displaystyle \end{aligned}$$

(13)

In this paper, we only deal with the equilibrium point $U_{1}(u_{1\star},u_{2\star}, u_{3\star})$. For the equilibrium point $U_{2} (-u_{1\star},u_{2\star}, -u_{3\star} )$, we can deal with it in a similar method. The linear system of model (5) around $U_{1}(u_{1\star},u_{2\star}, u_{3\star})$ takes the following expression:

$$\begin{aligned}& \textstyle\begin{cases} \dot{u}_{1}(t)=(u_{2\star}-\alpha)u_{1}(t)+u_{3}(t)+u_{1 \star}u_{2}(t-\sigma), \\ \dot{u}_{2}(t)=-2u_{1\star}u_{1}(t)-\beta u_{2}(t- \sigma), \\ \dot{u}_{3}(t)=-u_{1}(t)-\gamma u_{3}(t). \end{cases}\displaystyle \end{aligned}$$

(14)

The characteristic equation of system (14) owns the following expression:

$$det\left[\begin{array}{ccc}\lambda -(u_{2\star }-\alpha )& -u_{1\star }{e}^{-\lambda \sigma }& -1\\ 2u_{1\star }& \lambda +\beta e^{-\lambda \sigma }& 0\\ 1& 0& \lambda +\gamma \end{array}\right]=0,$$

(15)

which generates

$$\begin{aligned}& \lambda^{3}+a_{1}\lambda^{2}+a_{2} \lambda+\bigl(a_{3}\lambda^{2}+a_{4} \lambda+a_{5}\bigr)e^{-\lambda\sigma}=0, \end{aligned}$$

(16)

where

$$\begin{aligned}& \textstyle\begin{cases} a_{1}=\gamma-u_{2\star}+\alpha, \\ a_{2}=1-\gamma(u_{2\star}-\alpha), \\ a_{3}=\beta, \\ a_{4}=2u_{1\star}^{2}-(u_{2\star}-\alpha)\beta+\beta \gamma, \\ a_{5}=2u_{1\star}^{2}\gamma-\gamma\beta(u_{2\star}- \alpha). \end{cases}\displaystyle \end{aligned}$$

(17)

When $\sigma=0$, then Eq. (16) becomes:

$$\begin{aligned}& \lambda^{3}+(a_{1}+a_{3})\lambda^{2}+(a_{2}+a_{4}) \lambda+a_{5}=0, \end{aligned}$$

(18)

If

$$({\mathcal{C}}_2)\{\begin{array}{c}{\mathcal{A}}_1=a_1+a_3>0,\hfill \\ {\mathcal{A}}_2=det\left[\begin{array}{cc}{a}_1+a_3& 1\\ a_5& a_2+a_4\end{array}\right]>0,\hfill \\ {\mathcal{A}}_3=a_5{\mathcal{A}}_2>0\hfill \end{array}$$

is fulfilled, then the three roots $\lambda_{1}$, $\lambda_{2}$, $\lambda_{3}$ of Eq. (18) have negative real parts. Thus the equilibrium point $U_{1}(u_{1\star},u_{2\star}, u_{3\star})$ of system (5) with $\sigma=0$ is locally asymptotically stable.

Suppose that $\lambda=i\zeta$ is the root of Eq. (16). Then Eq. (16) becomes:

$$\begin{aligned}& (i\zeta)^{3}+a_{1}(i\zeta)^{2}+a_{2}i \zeta+\bigl[a_{3}(i\zeta)^{2}+a_{4}i \zeta+a_{5}\bigr]e^{-i\zeta\sigma}=0, \end{aligned}$$

(19)

which generates

$$\begin{aligned}& -i\zeta^{3}-a_{1}\zeta^{2}+a_{2}\zeta i+\bigl[-a_{3}\zeta^{2}+a_{4} \zeta i+a_{5}\bigr]e^{-i\zeta\sigma}=0. \end{aligned}$$

(20)

It follows from (20) that

$$\begin{aligned}& \textstyle\begin{cases} (a_{5}-a_{3}\zeta^{2})\cos\zeta\sigma+a_{4}\zeta \sin\zeta\sigma=a_{1}\zeta^{2}, \\ a_{4}\zeta\cos\zeta\sigma-(a_{5}-a_{3}\zeta^{2}) \sin\zeta\sigma= \zeta^{3}-a_{2}\zeta, \end{cases}\displaystyle \end{aligned}$$

(21)

By (21), we have

$$\begin{aligned}& \bigl(a_{5}-a_{3}\zeta^{2}\bigr)^{2}+(a_{4} \zeta)^{2}=\bigl(a_{1}\zeta^{2} \bigr)^{2}+\bigl( \zeta^{3}-a_{2}\zeta \bigr)^{2}, \end{aligned}$$

(22)

which means

$$\begin{aligned}& \zeta^{6}+\bigl(a_{1}^{2}-a_{3}^{2}-2a_{2} \bigr)\zeta ^{4}+\bigl(a_{2}^{2}-a_{4}^{2}+2a_{3}a_{5} \bigr) \zeta^{2}-a_{5}^{2}=0. \end{aligned}$$

(23)

Let

$$\begin{aligned}& \Pi(\zeta)=\zeta^{6}+\bigl(a_{1}^{2}-a_{3}^{2}-2a_{2} \bigr)\zeta ^{4}+\bigl(a_{2}^{2}-a_{4}^{2}+2a_{3}a_{5} \bigr) \zeta^{2}-a_{5}^{2}. \end{aligned}$$

(24)

Since $\Pi(0)=-a_{5}^{2}<0$ and $\lim_{\zeta\rightarrow+\infty}\Pi(\zeta)=+\infty>0$, then we know that Eq. (23) has at least one positive real root. Thus Eq. (16) has at least one pure root pair. Without loss of generality, we assume that Eq. (23) has six positive real roots (say $\zeta_{j}$, $j=1,2,\ldots ,6$). According to (21), we have

$$\begin{aligned}& \sigma_{j}^{(h)}=\frac{1}{\zeta_{j}} \biggl[\arccos \biggl( \frac{a_{1}\zeta_{j}^{2}(a_{5}-a_{3}\zeta_{j}^{2})+a_{4}\zeta _{j}(\zeta_{j}^{3}-a_{2}\zeta_{j})}{ (a_{5}-a_{3}\zeta_{j}^{2})^{2}+a_{4}^{2}\zeta_{j}^{2}} \biggr)+2h \pi \biggr], \end{aligned}$$

(25)

where $j=1,2,3,4,5,6$; $h=0,1,2,\ldots$ . Denote $\sigma_{0}=\min_{\{j=1,2,3,4,5,6; h=0,1,2,\ldots\}}\{\sigma_{j}^{(h)} \}$ and assume that when $\sigma=\sigma_{0}$, (16) has a pair of imaginary roots $\pm i\zeta_{0}$.

Now we give the following hypothesis:

$$\begin{aligned}& ({\mathcal{C}}_{3})\quad {\mathcal{G}}_{1R}{\mathcal{G}}_{2R}+{ \mathcal{G}}_{1I}{ \mathcal{G}}_{2I}>0, \end{aligned}$$

where

$$\begin{aligned}& \textstyle\begin{cases} {\mathcal{G}}_{1R}=a_{2}+a_{4}\cos\zeta_{0}\sigma_{0}+2a_{3} \zeta_{0}\sin\zeta_{0}\sigma_{0}, \\ {\mathcal{G}}_{1I}=2a_{1}\zeta_{0}-3\zeta_{0}^{2}+2a_{3} \zeta_{0}\cos\zeta_{0}\sigma_{0}-a_{4}\sin\zeta_{0}\sigma_{0}, \\ {\mathcal{G}}_{2R}=(a_{5}-a_{3}\zeta_{0}^{2})\zeta_{0} \sin\zeta_{0}\sigma_{0}-a_{4}\zeta_{0}\cos\zeta_{0}\sigma_{0}, \\ {\mathcal{G}}_{2I}=(a_{5}-a_{3}\zeta_{0}^{2})\zeta_{0} \cos\zeta_{0}\sigma_{0}+a_{4}\zeta_{0}\sin\zeta_{0}\sigma_{0}. \end{cases}\displaystyle \end{aligned}$$

(26)

Lemma 1

Suppose that $s(\sigma)=\epsilon_{1}(\sigma)+i\epsilon_{2}(\sigma)$ is the root of Eq. (16) at $\sigma=\sigma_{0}$ such that $\epsilon_{1}(\sigma_{0})=0$, $\epsilon_{2}(\sigma_{0})=\zeta_{0}$, then $\operatorname{Re} (\frac{ds}{d\sigma} ) |_{\sigma=\sigma _{0},\zeta= \zeta_{0}}>0$.

Proof

By Eq. (16), one gets

$$\begin{aligned}& \bigl(3\lambda^{2}+2a_{1}\lambda+a_{2} \bigr) \frac{d\lambda}{d\sigma}+(2a_{3}\lambda+a_{4})e^{-\lambda\sigma} \frac{ds}{d\sigma} \\& \quad {}-e^{-\lambda\sigma} \biggl(\frac{ds}{d\sigma}\sigma+\lambda \biggr) \bigl(a_{3}\lambda^{2}+a_{4}\lambda+a_{5} \bigr)=0, \end{aligned}$$

(27)

which implies

$$\begin{aligned}& \biggl(\frac{d\lambda}{d\sigma} \biggr)^{-1}= \frac{{\mathcal{G}}_{1}(\lambda)}{{\mathcal{G}}_{2}(\lambda)}- \frac{\sigma}{s}, \end{aligned}$$

(28)

where

$$\begin{aligned}& \textstyle\begin{cases} {\mathcal{G}}_{1}(\lambda)=3\lambda^{2}+2a_{1} \lambda+a_{2}+(2a_{3}\lambda+a_{4})e^{-\lambda\sigma}, \\ {\mathcal{G}}_{2}(\lambda)=\lambda e^{-\lambda\sigma} (a_{3}\lambda^{2}+a_{4}\lambda+a_{5} ). \end{cases}\displaystyle \end{aligned}$$

(29)

Hence

$$\begin{aligned}& \operatorname{Re} \biggl[ \biggl(\frac{d\lambda}{d\sigma} \biggr)^{-1} \biggr]_{ \sigma=\sigma_{0},\zeta=\zeta_{0}}=\operatorname{Re} \biggl[ \frac{{\mathcal{G}}_{1}(\lambda)}{{\mathcal{G}}_{2}(\lambda)} \biggr]_{\sigma=\sigma_{0},\zeta=\zeta_{0}} = \frac{{\mathcal{G}}_{1R}{\mathcal{G}}_{2R}+{\mathcal{G}}_{1I}{\mathcal {G}}_{2I}}{{\mathcal{G}}_{2R}^{2}+{\mathcal{I}}_{2I}^{2}}. \end{aligned}$$

(30)

Taking advantage of $({\mathcal{C}}_{3})$, one gets

$$\begin{aligned}& \operatorname{Re} \biggl[ \biggl(\frac{d\lambda}{d\sigma} \biggr)^{-1} \biggr]_{ \sigma=\sigma_{0},\zeta=\zeta_{0}}>0, \end{aligned}$$

(31)

which ends the proof. □

Based on the exploration above, then the following assertion can be easily derived.

Theorem 3

If $({\mathcal{C}}_{1})$–$({\mathcal{C}}_{3})$ holds, then the equilibrium point $U_{1}(u_{1\star},u_{2\star}, u_{3\star})$ of model (5) is locally asymptotically stable if $\sigma\in[0,\sigma_{0})$ and a Hopf bifurcation of model (5) happens near the equilibrium point $U_{1}(u_{1\star},u_{2\star}, u_{3\star})$ when $\sigma=\sigma_{0}$.

4 Bifurcation control of system (5) via hybrid control strategy

In this part, we will deal with the Hopf bifurcation problem of system (5) via a suitable hybrid controller consisting of state feedback and parameter perturbation. Taking advantage of the idea from [27, 28], we obtain the following controlled finance model:

$$\begin{aligned}& \textstyle\begin{cases} \dot{u}_{1}(t)=\rho_{1}[u_{3}(t)+(u_{2}(t-\sigma)- \alpha)u_{1}(t)]+\rho_{2}[u_{1}(t)-u_{1}(t-\sigma)], \\ \dot{u}_{2}(t)=\rho_{1}[1-\beta u_{2}(t-\sigma)-u_{1}^{2}(t)]+ \rho_{2}[u_{2}(t)-u_{2}(t-\sigma)], \\ \dot{u}_{3}(t)=\rho_{1}[-u_{1}(t)-\gamma u_{3}(t)]+ \rho_{2}[u_{3}(t)-u_{3}(t-\sigma)], \end{cases}\displaystyle \end{aligned}$$

(32)

where $\rho_{1}$, $\rho_{2}$ represent feedback gain parameters. System (32) and system (5) have the same equilibrium points. If $({\mathcal{C}}_{1})$ holds, then it is easy to derive that system (32) has the following two equilibrium points:

$$\begin{aligned}& U_{1}(u_{1\star},u_{2\star}, u_{3\star}),\qquad U_{2} (-u_{1\star},u_{2 \star}, -u_{3\star} ), \end{aligned}$$

In this paper, we only deal with the equilibrium point $U_{1}(u_{1\star},u_{2\star}, u_{3\star})$. For the equilibrium point $U_{2} (-u_{1\star},u_{2\star}, -u_{3\star} )$, we can deal with it in a similar method. The linear system of model (32) around $U_{1}(u_{1\star},u_{2\star}, u_{3\star})$ takes the following expression:

$$\begin{aligned}& \textstyle\begin{cases} \dot{u}_{1}(t)=[\rho_{1}(u_{2\star}-\alpha)+\rho_{2}]u_{1}(t)+ \rho_{1}u_{3}(t)-\rho_{2}u_{1}(t-\sigma)+\rho_{1}u_{1\star}u_{2}(t- \sigma), \\ \dot{u}_{2}(t)=-2\rho_{1}u_{1\star}u_{1}(t)+\rho_{2}u_{2}(t)-( \rho_{1}\beta+\rho_{2}) u_{2}(t-\sigma), \\ \dot{u}_{3}(t)=-\rho_{1}u_{1}(t)-(\gamma\rho_{1}- \rho_{2})u_{3}(t)-\rho_{2}u_{3}(t-\sigma). \end{cases}\displaystyle \end{aligned}$$

(33)

The characteristic equation of system (33) owns the following expression:

$$\begin{array}{c}det\left[\begin{array}{ccc}\lambda -[{\rho }_1(u_{2\star }-\alpha )+{\rho }_2]+{\rho }_2{e}^{-\lambda \sigma }& -{\rho }_1{u}_{1\star }{e}^{-\lambda \sigma }& -{\rho }_1\\ 2{\rho }_1{u}_{1\star }& \lambda -{\rho }_2+({\rho }_1\beta +{\rho }_2)e^{-\lambda \sigma }& 0\\ {\rho }_1& 0& \lambda +(\gamma {\rho }_1-{\rho }_2)+{\rho }_2{e}^{-\lambda \sigma }\end{array}\right]\hfill \\ =0,\hfill \end{array}$$

(34)

which generates

$$\begin{aligned}& \lambda^{3}+b_{1}\lambda^{2}+b_{2} \lambda+b_{3}+\bigl(b_{4}\lambda^{2}+b_{5} \lambda+b_{6}\bigr)e^{-\lambda\sigma}+(b_{7} \lambda+b_{8})e^{-2\lambda \sigma}+b_{9}e^{-3\lambda\sigma}=0, \end{aligned}$$

(35)

where

$$\begin{aligned}& \textstyle\begin{cases} b_{1}=(\gamma-1)\rho_{1}-2\rho_{2}-\rho_{1}(u_{2 \star}-\alpha), \\ b_{2}=\rho_{2}[\rho_{1}(u_{2\star}-\alpha)+\rho_{2}]+ \rho_{1}^{2} \\ \hphantom{b_{2}=}{}-(\gamma\rho_{1}-\rho_{2})[\rho_{1}(u_{2\star}- \alpha)+\rho_{1}+\rho_{2}], \\ b_{3}=\rho_{1}(\gamma\rho_{1}-\rho_{2})[\rho_{1}(u_{2 \star}-\alpha)+\rho_{2}]-\rho_{1}^{2}\rho_{2}, \\ b_{4}=2\rho_{2}+\rho_{1}\beta+\rho_{2}, \\ b_{5}=(2\rho_{2}+\rho_{1}\beta)(\gamma\rho_{1}- \rho_{2})-\rho_{2}^{2}+2\rho_{1}^{2}u_{1\star}^{2} \\ \hphantom{b_{5}=}{}-[\rho_{1}(u_{2\star}-\alpha)+\rho_{2}](\rho_{1} \beta+\rho_{2}) \\ \hphantom{b_{5}=}{}-\rho_{2}[\rho_{1}(u_{2\star}-\alpha)+\rho_{1}+ \rho_{2}], \\ b_{6}=\rho_{2}^{2}[\rho_{1}(u_{2\star}-\alpha)+\rho_{2}]+ \rho_{1}^{2}(\rho_{1}\beta+\rho_{2}) \\ \hphantom{b_{6}=}{}-\{\rho_{2}^{2}+[\rho_{1}(u_{2\star}-\alpha)+ \rho_{2}](\rho_{1}\beta+\rho_{2})\} \\ \hphantom{b_{6}=}{}\times(\gamma\rho_{1}-\rho_{2})+2\rho_{1}^{2}u_{1 \star}^{2}(\gamma\rho_{1}-\rho_{2}), \\ b_{7}=\rho_{2}(\rho_{1}\beta+\rho_{2})+\rho_{2}(2 \rho_{2}+\rho_{1}\beta), \\ b_{8}=\rho_{2}(\gamma\rho_{1}-\rho_{2})(\rho_{1} \beta+\rho_{2})+2\rho_{2}\rho_{1}^{2}u_{1\star}^{2} \\ \hphantom{b_{8}=}{}-\rho_{1}\{\rho_{2}^{2}+[\rho_{1}(u_{2\star}- \alpha)+\rho_{2}](\rho_{1}\beta+\rho_{2})\}, \\ b_{9}=\rho_{2}^{2}(\rho_{1}\beta+\rho_{2}). \end{cases}\displaystyle \end{aligned}$$

(36)

When $\sigma=0$, then Eq. (35) becomes:

$$\begin{aligned}& \lambda^{3}+(b_{1}+b_{4})\lambda^{2}+(b_{2}+b_{5}+b_{7}) \lambda +b_{3}+b_{6}+b_{9}=0, \end{aligned}$$

(37)

If

$$({\mathcal{C}}_4)\{\begin{array}{c}{\mathcal{B}}_1=b_1+b_4>0,\hfill \\ {\mathcal{B}}_2=det\left[\begin{array}{cc}{b}_1+b_4& 1\\ b_3+b_6+b_9& b_2+b_5+b_7\end{array}\right]>0,\hfill \\ {\mathcal{B}}_3=(b_3+b_6+b_9){\mathcal{B}}_2>0\hfill \end{array}$$

is fulfilled, then the three roots $\lambda_{1}$, $\lambda_{2}$, $\lambda_{3}$ of Eq. (37) have negative real parts. Thus the equilibrium point $U_{1}(u_{1\star},u_{2\star}, u_{3\star})$ of system (32) with $\sigma=0$ is locally asymptotically stable.

Equation (35) can be rewritten in the following form:

$$\begin{aligned}& \bigl(\lambda^{3}+b_{1}\lambda^{2}+b_{2} \lambda+b_{3}\bigr)e^{\lambda\sigma}+\bigl(b_{4} \lambda^{2}+b_{5}\lambda+b_{6}\bigr)+(b_{7} \lambda+b_{8})e^{-\lambda \sigma}+b_{9}e^{-2\lambda\sigma}=0. \end{aligned}$$

(38)

Suppose that $\lambda=i\varsigma$ is the root of Eq. (38). Then Eq. (38) becomes:

$$\begin{aligned}& \bigl[(i\varsigma)^{3}+b_{1}(i\varsigma)^{2}+b_{2}i \varsigma+b_{3}\bigr]e^{i \varsigma\sigma}+\bigl[b_{4}(i \varsigma)^{2}+b_{5}i\varsigma+b_{6}\bigr] \\& \quad {}+(b_{7}i \varsigma+b_{8})e^{-i\varsigma\sigma}+b_{9}e^{-2i\varsigma\sigma}=0, \end{aligned}$$

(39)

which generates

$$\begin{aligned}& \textstyle\begin{cases} (b_{3}+b_{8}-b_{1}\varsigma^{2})\cos\varsigma\sigma+(b_{7} \varsigma-b_{2}\varsigma+\varsigma^{3})\sin\varsigma\sigma+b_{6}-b_{4} \varsigma^{2}=-b_{9}\cos2\varsigma\sigma, \\ (b_{2}\varsigma+b_{8}-\varsigma^{3}+b_{7}\varsigma) \cos\varsigma\sigma+(b_{3}-b_{8}-b_{1}\varsigma^{2})\sin \varsigma\sigma+b_{5}\varsigma=b_{9}\sin2\varsigma\sigma. \end{cases}\displaystyle \end{aligned}$$

(40)

By (40), we have

$$\begin{aligned}& \bigl[\bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr)\cos\varsigma\sigma+\bigl(b_{7} \varsigma-b_{2}\varsigma+\varsigma^{3}\bigr)\sin\varsigma \sigma+b_{6}-b_{4} \varsigma^{2} \bigr]^{2} \\& \quad {}+\bigl[\bigl(b_{2}\varsigma+b_{8}- \varsigma^{3}+b_{7}\varsigma\bigr)\cos \varsigma\sigma+ \bigl(b_{3}-b_{8}-b_{1}\varsigma^{2} \bigr)\sin\varsigma \sigma+b_{5}\varsigma\bigr]^{2}=b_{9}^{2}, \end{aligned}$$

(41)

which means

$$\begin{aligned}& \bigl[\bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr)^{2}+\bigl(b_{2} \varsigma+b_{8}- \varsigma^{3}+b_{7}\varsigma \bigr)^{2}\bigr]\cos^{2}\varsigma\sigma \\& \quad {}+\bigl[\bigl(b_{7}\varsigma-b_{2}\varsigma+ \varsigma^{3}\bigr)^{2}+\bigl(b_{3}-b_{8}-b_{1} \varsigma^{2}\bigr)^{2}\bigr]\sin^{2}\varsigma \sigma \\& \quad {}+2\bigl[\bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr) \bigl(b_{7}\varsigma-b_{2} \varsigma+\varsigma^{3}\bigr) \\& \quad {}+\bigl(b_{2}\varsigma+b_{8}- \varsigma^{3}+b_{7} \varsigma\bigr) \bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr)\bigr] \\& \quad {}\times\sin\varsigma\sigma\cos\varsigma\sigma+2\bigl[b_{5} \varsigma\bigl(b_{2}\varsigma+b_{8}-\varsigma^{3}+b_{7} \varsigma\bigr)-b_{4} \varsigma^{2}\bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr)\bigr]\cos\varsigma \sigma \\& \quad {}+2\bigl[\bigl(b_{6}-b_{4}\varsigma^{2} \bigr) \bigl(b_{7}\varsigma-b_{2}\varsigma+ \varsigma^{3}\bigr)+b_{5}\varsigma\bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr)\bigr] \sin\varsigma\sigma \\& \quad {}+\bigl(b_{6}-b_{4}\varsigma^{2} \bigr)^{2}+(b_{5}\varsigma)^{2}-b_{9}^{2}=0. \end{aligned}$$

(42)

It follows from (42) that

$$\begin{aligned}& \bigl[\bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr)^{2}+\bigl(b_{2} \varsigma+b_{8}- \varsigma^{3}+b_{7}\varsigma \bigr)^{2} \\& \quad {}+\bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr) \bigl(b_{7}\varsigma-b_{2} \varsigma+ \varsigma^{3}\bigr) \\& \quad {}+\bigl(b_{2}\varsigma+b_{8}-\varsigma^{3}+b_{7} \varsigma\bigr) \bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr)\bigr]\cos^{2}\varsigma\sigma \\& \quad {}+\bigl[\bigl(b_{7}\varsigma-b_{2}\varsigma+ \varsigma^{3}\bigr)^{2}+\bigl(b_{3}-b_{8}-b_{1} \varsigma^{2}\bigr)^{2} \\& \quad {}-\bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr) \bigl(b_{7}\varsigma-b_{2} \varsigma+ \varsigma^{3}\bigr) \\& \quad {}-\bigl(b_{2}\varsigma+b_{8}-\varsigma^{3}+b_{7} \varsigma\bigr) \bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr)\bigr]\sin^{2}\varsigma\sigma \\& \quad {}+2\bigl[b_{5}\varsigma\bigl(b_{2} \varsigma+b_{8}-\varsigma^{3}+b_{7} \varsigma \bigr)-b_{4}\varsigma^{2}\bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr)\bigr] \cos\varsigma\sigma \\& \quad {}+2\bigl[\bigl(b_{6}-b_{4}\varsigma^{2} \bigr) \bigl(b_{7}\varsigma-b_{2}\varsigma+ \varsigma^{3}\bigr)+b_{5}\varsigma\bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr)\bigr] \sin\varsigma\sigma \\& \quad {}+\bigl(b_{6}-b_{4}\varsigma^{2} \bigr)^{2}+(b_{5}\varsigma)^{2}-b_{9}^{2}=0. \end{aligned}$$

(43)

In view of $\sin\varsigma\sigma=\pm\sqrt{1-\cos^{2}\varsigma\sigma}$, (43) takes the form:

$$\begin{aligned}& \bigl[\bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr)^{2}+\bigl(b_{2} \varsigma+b_{8}- \varsigma^{3}+b_{7}\varsigma \bigr)^{2} \\& \quad {}+\bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr) \bigl(b_{7}\varsigma-b_{2} \varsigma+ \varsigma^{3}\bigr) \\& \quad {}+\bigl(b_{2}\varsigma+b_{8}-\varsigma^{3}+b_{7} \varsigma\bigr) \bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr)\bigr]\cos^{2}\varsigma\sigma \\& \quad {}+\bigl[\bigl(b_{7}\varsigma-b_{2}\varsigma+ \varsigma^{3}\bigr)^{2}+\bigl(b_{3}-b_{8}-b_{1} \varsigma^{2}\bigr)^{2} \\& \quad {}-\bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr) \bigl(b_{7}\varsigma-b_{2} \varsigma+ \varsigma^{3}\bigr) \\& \quad {}-\bigl(b_{2}\varsigma+b_{8}-\varsigma^{3}+b_{7} \varsigma\bigr) \bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr)\bigr]\sin^{2}\varsigma\sigma \\& \quad {}+2\bigl[b_{5}\varsigma\bigl(b_{2} \varsigma+b_{8}-\varsigma^{3}+b_{7} \varsigma \bigr)-b_{4}\varsigma^{2}\bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr)\bigr] \cos\varsigma\sigma \\& \quad {}+2\bigl[\bigl(b_{6}-b_{4}\varsigma^{2} \bigr) \bigl(b_{7}\varsigma-b_{2}\varsigma+ \varsigma^{3}\bigr)+b_{5}\varsigma\bigl(b_{3}+b_{8}-b_{1} \varsigma^{2}\bigr)\bigr]\bigl( \pm\sqrt{1-\cos^{2}\varsigma \sigma}\bigr) \\& \quad {}+\bigl(b_{6}-b_{4}\varsigma^{2} \bigr)^{2}+(b_{5}\varsigma)^{2}-b_{9}^{2}=0. \end{aligned}$$

(44)

In (44), we denote

$$\begin{aligned}& \textstyle\begin{cases} c_{1}=(b_{3}+b_{8}-b_{1}\varsigma^{2})^{2}+(b_{2} \varsigma+b_{8}-\varsigma^{3}+b_{7}\varsigma)^{2} \\ \hphantom{c_{1}=}{}+(b_{3}+b_{8}-b_{1}\varsigma^{2})(b_{7} \varsigma-b_{2}\varsigma+\varsigma^{3}) \\ \hphantom{c_{1}=}{}\times (b_{2}\varsigma+b_{8}-\varsigma^{3}+b_{7} \varsigma)(b_{3}+b_{8}-b_{1}\varsigma^{2}), \\ c_{2}=(b_{7}\varsigma-b_{2}\varsigma+\varsigma^{3})^{2}+(b_{3}-b_{8}-b_{1} \varsigma^{2})^{2} \\ \hphantom{c_{2}=}{}-(b_{3}+b_{8}-b_{1}\varsigma^{2})(b_{7} \varsigma-b_{2}\varsigma+\varsigma^{3}) \\ \hphantom{c_{2}=}{}-(b_{2}\varsigma+b_{8}-\varsigma^{3}+b_{7} \varsigma)(b_{3}+b_{8}-b_{1}\varsigma^{2}), \\ c_{3}=2[b_{5}\varsigma(b_{2}\varsigma+b_{8}- \varsigma^{3}+b_{7}\varsigma)-b_{4}\varsigma^{2}(b_{3}+b_{8}-b_{1} \varsigma^{2})], \\ c_{4}=2[(b_{6}-b_{4}\varsigma^{2})(b_{7}\varsigma-b_{2} \varsigma+\varsigma^{3})+b_{5}\varsigma(b_{3}+b_{8}-b_{1} \varsigma^{2})], \\ c_{5}=(b_{6}-b_{4}\varsigma^{2})^{2}+(b_{5}\varsigma)^{2}-b_{9}^{2}, \end{cases}\displaystyle \end{aligned}$$

(45)

then (44) becomes

$$\begin{aligned}& c_{1}\cos^{2}\varsigma\sigma+c_{2} \sin^{2}\varsigma\sigma+c_{3} \cos\varsigma \sigma+c_{4}\bigl(\pm\sqrt{1-\cos^{2}\varsigma\sigma} \bigr)+c_{5}=0. \end{aligned}$$

(46)

Then

$$\begin{aligned}& (c_{1}-c_{2})\cos^{2}\varsigma \sigma+c_{3}\cos\varsigma\sigma +c_{2}+c_{5}=c_{4} \bigl( \pm\sqrt{1-\cos^{2}\varsigma\sigma}\bigr), \end{aligned}$$

(47)

which leads to

$$\begin{aligned}& d_{1}\cos^{3}\varsigma\sigma+d_{2} \cos^{3}\varsigma\sigma+d_{3} \cos^{2}\varsigma \sigma+d_{4}\cos\varsigma\sigma+d_{5}=0, \end{aligned}$$

(48)

where

$$\begin{aligned}& \textstyle\begin{cases} d_{1}=(c_{1}-c-2)^{2}, \\ d_{2}=2c_{3}(c_{1}-c_{2}), \\ d_{3}=2(c_{1}-c_{2})(c_{2}-c_{5})+c_{3}^{2}+c_{4}^{2}, \\ d_{4}=2c_{3}(c_{2}+c_{5}), \\ d_{5}=(c_{2}+c_{4})^{2}-c_{4}^{2}. \end{cases}\displaystyle \end{aligned}$$

(49)

By virtue of computer software, we can solve the value of $\cos\varsigma\sigma$. Here we assume that

$$\begin{aligned}& \cos\varsigma\sigma=f_{1}(\varsigma). \end{aligned}$$

(50)

Then we can solve the value of $\sin\varsigma\sigma$. Here we assume that

$$\begin{aligned}& \sin\varsigma\sigma=f_{2}(\varsigma). \end{aligned}$$

(51)

Using (50) and (51), we have

$$\begin{aligned}& f_{1}^{2}(\varsigma)+f_{2}^{2}( \varsigma)=1. \end{aligned}$$

(52)

By virtue of (52), we can easily obtain the value of ς (say $\varsigma_{0}$). According to (50), we get

$$\begin{aligned}& \sigma_{k}=\frac{1}{\varsigma_{0}}\bigl[\arccos f_{1}( \varsigma_{0})+2k \pi\bigr], \quad k=0,1,2,\ldots. \end{aligned}$$

(53)

Denote

$$\begin{aligned}& \sigma_{\star}= \min_{\{k=0,1,2,\ldots\}}\{\sigma_{k}\}. \end{aligned}$$

(54)

Now we know that when $\sigma=\sigma_{\star}$, (35) has a pair of imaginary roots $\pm i\varsigma_{0}$.

Now we give the following hypothesis:

$$\begin{aligned}& ({\mathcal{C}}_{5})\quad {\mathcal{H}}_{1R}{ \mathcal{H}}_{2R}+{\mathcal{H}}_{1I}{ \mathcal{H}}_{2I}>0, \end{aligned}$$

where

$$\begin{aligned}& \textstyle\begin{cases} {\mathcal{H}}_{1R}=b_{2}-3\varsigma_{0}^{2}+b_{5}\cos \varsigma_{0}\sigma_{\star}+2b_{4}\sin\varsigma_{0}\sigma_{\star}+b_{7} \cos2\varsigma_{0}\sigma_{\star}, \\ {\mathcal{H}}_{1I}=2b_{1}\varsigma_{0}-b_{5}\sin \varsigma_{0}\sigma_{\star}+2b_{4}\cos\varsigma_{0}\sigma_{\star}-b_{7} \sin2\varsigma_{0}\sigma_{\star}, \\ {\mathcal{H}}_{2R}=(b_{5}-b_{4}\varsigma_{0}^{2}) \varsigma_{0}\sin\varsigma_{0}\sigma_{\star}-b_{5}\varsigma_{0}^{2} \cos\varsigma_{0}\sigma_{\star}+3b_{9}\varsigma_{0}\sin3 \varsigma_{0}\sigma_{\star} \\ \hphantom{{\mathcal{H}}_{2R}=}{}+2b_{8}\varsigma_{0}\sin2\varsigma_{0} \sigma_{\star}-2b_{7}\varsigma_{0}\cos2\varsigma_{0}\sigma_{ \star}, \\ {\mathcal{H}}_{2I}=(b_{5}-b_{4}\varsigma_{0}^{2}) \varsigma_{0}\cos\varsigma_{0}\sigma_{\star}+b_{5}\varsigma_{0}^{2} \sin\varsigma_{0}\sigma_{\star}+3b_{9}\varsigma_{0}\cos3 \varsigma_{0}\sigma_{\star} \\ \hphantom{{\mathcal{H}}_{2I}=}{}+2b_{7}\varsigma_{0}\sin2\varsigma_{0} \sigma_{\star}+2b_{8}\varsigma_{0}\cos2\varsigma_{0}\sigma_{ \star}. \end{cases}\displaystyle \end{aligned}$$

(55)

Lemma 2

Suppose that $s(\sigma)=\varepsilon_{1}(\sigma)+i\varepsilon_{2}(\sigma)$ is the root of Eq. (35) at $\sigma=\sigma_{\star}$ such that $\varepsilon_{1}(\sigma_{\star})=0$, $\varepsilon_{2}(\sigma_{ \star})=\varsigma_{0}$, then $\operatorname{Re} (\frac{ds}{d\sigma} ) |_{\sigma =\sigma_{\star}, \varsigma=\varsigma_{0}}>0$.

Proof

By Eq. (35), one gets

$$\begin{aligned}& \bigl(3\lambda^{2}+2b_{1}\lambda+b_{2} \bigr) \frac{d\lambda}{d\sigma}+(2b_{4}\lambda+b_{5})e^{-\lambda\sigma} \frac{ds}{d\sigma} \\& \quad {}-e^{-\lambda\sigma} \biggl(\frac{ds}{d\sigma}\sigma+\lambda \biggr) \bigl(b_{4}\lambda^{2}+b_{5}\lambda+b_{6} \bigr)+b_{7}e^{-2 \lambda\sigma}\frac{ds}{d\sigma} \\& \quad {}-2e^{-2\lambda\sigma} \biggl(\frac{ds}{d\sigma}\sigma+\lambda \biggr) (b_{7}\lambda+b_{8})-3b_{9}e^{-3\lambda\sigma} \biggl( \frac{ds}{d\sigma}\sigma+\lambda \biggr)=0, \end{aligned}$$

(56)

which implies

$$\begin{aligned}& \biggl(\frac{d\lambda}{d\sigma} \biggr)^{-1}= \frac{{\mathcal{H}}_{1}(\lambda)}{{\mathcal{H}}_{2}(\lambda)}- \frac{\sigma}{s}, \end{aligned}$$

(57)

where

$$\begin{aligned}& \textstyle\begin{cases} {\mathcal{H}}_{1}(\lambda)=3\lambda^{2}+2b_{1} \lambda+b_{2}+(2b_{4}\lambda+b_{5})e^{-\lambda\sigma}+b_{7}e^{-2 \lambda\sigma}, \\ {\mathcal{H}}_{2}(\lambda)=\lambda e^{-\lambda\sigma} (b_{4}\lambda^{2}+b_{4}\lambda+b_{6} )+2\lambda e^{-2 \lambda\sigma} (b_{7}\lambda+b_{8} )+3\lambda b_{9}e^{-3 \lambda\sigma}. \end{cases}\displaystyle \end{aligned}$$

(58)

Hence

$$\begin{aligned} \operatorname{Re} \biggl[ \biggl(\frac{d\lambda}{d\sigma} \biggr)^{-1} \biggr]_{ \sigma=\sigma_{\star},\varsigma=\varsigma_{0}} =&\operatorname{Re} \biggl[ \frac{{\mathcal{H}}_{1}(\lambda)}{{\mathcal{H}}_{2}(\lambda)} \biggr]_{\sigma=\sigma_{\star},\varsigma=\varsigma_{0}} \\ =& \frac{{\mathcal{H}}_{1R}{\mathcal{H}}_{2R}+{\mathcal{H}}_{1I}{\mathcal {H}}_{2I}}{{\mathcal{H}}_{2R}^{2}+{\mathcal{H}}_{2I}^{2}}. \end{aligned}$$

(59)

Taking advantage of $({\mathcal{C}}_{5})$, one gets

$$\begin{aligned}& \operatorname{Re} \biggl[ \biggl(\frac{d\lambda}{d\sigma} \biggr)^{-1} \biggr]_{ \sigma=\sigma_{\star},\varsigma=\varsigma_{0}}>0, \end{aligned}$$

(60)

which ends the proof. □

Based on the exploration above, the following assertion can be easily derived.

Theorem 4

If $({\mathcal{C}}_{1})$, $({\mathcal{C}}_{4})$, $({\mathcal{C}}_{5})$ holds, then the equilibrium point $U_{1}(u_{1\star},u_{2\star}, u_{3\star})$ of model (32) is locally asymptotically stable if $\sigma\in[0,\sigma_{\star})$ and a Hopf bifurcation of model (32) happens near the equilibrium point $U_{1}(u_{1\star},u_{2\star}, u_{3\star})$ when $\sigma=\sigma_{\star}$.

Remark 1

In 2011, Wang et al. [8] explored the single-period, multiple-period, and chaotic motions of a fractional-order delayed finance model. In 2014, Chen et al. [9] discussed the stability of the unique equilibrium and Hopf bifurcation problem of another delayed finance model. In this work, we establish a new delayed finance model, which is different from the delayed finance models in [8, 9]. We explore the existence, uniqueness, and boundedness of the solution, Hopf bifurcation, and Hopf bifurcation control aspect of the established the delayed finance model (5). The research method in [8, 9] cannot be applied to model (5) to derive the results of this article. Based on this fact, we think that our studies supplement the works of [8, 9] to some degree.

Remark 2

In model (5), there is only one delay. If there exist two different delays, we can also deal with the bifurcation issue of this model. We leave this topic for future research direction.

Remark 3

In this paper, we deal with Hopf bifurcation control via hybrid control strategy. Of course, there are many other control techniques for the model (5), for example, delayed feedback control, state feedback control, PD control and so on. We will explore this aspect in near future.

Remark 4

In this paper, there are some very complex assumptions(for example, $({\mathcal{C}}_{5})$, etc.). We can check the correctness of these assumptions via computer.

Remark 5

In Sect. 4, the hybrid control strategy is applied to control Hopf bifurcation of model (5). In (32), there are two same parameters in three controllers in three equations. Also we can use different parameters in three controllers in three equations.

Remark 6

Although there have been many works on Hopf bifurcation and control aspect of delayed dynamical models in past decades, the three hybrid controllers (consisting of state feedback and parameter perturbation) applied to the dynamical model are very few. Thus this controller is new.

5 Two illustrated examples

In this section, we will carry out numerical simulations via Matlab software.

Example 1

Consider the following delayed finance model:

$$\begin{aligned}& \textstyle\begin{cases} \dot{u}_{1}(t)=u_{3}(t)+(u_{2}(t-\sigma)-0.6)u_{1}(t), \\ \dot{u}_{2}(t)=1-0.2 u_{2}(t-\sigma)-u_{1}^{2}(t), \\ \dot{u}_{3}(t)=-u_{1}(t)-6 u_{3}(t). \end{cases}\displaystyle \end{aligned}$$

(61)

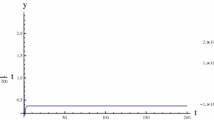
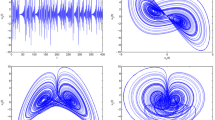
Clearly, system (61) has the equilibrium point $(0.9202,0.7667,-0.1534)$. One can easily verify that the conditions $({\mathcal{C}}_{1})$–$({\mathcal{C}}_{3})$ of Theorem 3 are fulfilled. By virtue of computer, we can determine that $\zeta_{0}=3.0092$, $\sigma_{0}\approx0.08$. To verify the right of the main results of Theorem 3, we choose both time delay values. One is $\sigma=0.06$ and the other is $\sigma=0.11$. For $\sigma=0.06<\sigma_{0}\approx0.08$, we get numerical simulation results which are presented in Fig. 1. In Fig. 1, we can see that $u_{1}\rightarrow0.9202$, $u_{2}\rightarrow0.7667$, $u_{2}\rightarrow-0.1534$ when $t\rightarrow+\infty$. That is to say, the equilibrium point $(0.9202,0.7667,-0.1534)$ of system (61) is locally asymptotically stable. For $\sigma=0.11>\sigma_{0}\approx0.08$, we get numerical simulation results which are presented in Fig. 2. In Fig. 2, we can see that $u_{1}$ will keep periodic vibration around the value 0.9202, $u_{2}$ will keep periodic vibration around the value 0.7667 and $u_{2}$ will keep periodic vibration around the value −0.1534. That is to say, a Hopf bifurcation appears near the equilibrium point $(0.9202,0.7667,-0.1534)$. Moreover, the bifurcation plots, which clearly display the bifurcation value of system (61), are presented in Figs. 3–5. In Figs. 3–5, we can see that the bifurcation value of system (61) $\sigma_{0}\approx0.08$.

Figure 1

Computer simulation figures of system (61) with $\sigma=0.06<\sigma_{0}\approx0.08$. The equilibrium point $(0.9202,0.7667,-0.1534)$ is locally asymptotically stable state.

Figure 2

Computer simulation figures of system (61) with $\sigma=0.11>\sigma_{0}\approx0.08$. A Hopf bifurcation takes place around the equilibrium point $(0.9202,0.7667,-0.1534)$.

Figure 3

Bifurcation diagram of system (61): t-$u_{1}$. The bifurcation value $\sigma_{0}\approx0.08$.

Figure 4

Bifurcation diagram of system (61): t-$u_{2}$. The bifurcation value $\sigma_{0}\approx0.08$.

Figure 5

Bifurcation diagram of system (61): t-$u_{3}$. The bifurcation value $\sigma_{0}\approx0.08$.

Example 2

Consider the following controlled delayed finance model:

$$\begin{aligned}& \textstyle\begin{cases} \dot{u}_{1}(t)=0.4[u_{3}(t)+(u_{2}(t-\sigma )-0.6)u_{1}(t)]+0.2[u_{1}(t)-u_{1}(t- \sigma)], \\ \dot{u}_{2}(t)=0.4[1-0.2 u_{2}(t-\sigma)-u_{1}^{2}(t)]+0.2[u_{2}(t)-u_{2}(t- \sigma)], \\ \dot{u}_{3}(t)=0.4[-u_{1}(t)-6 u_{3}(t)]+0.2[u_{3}(t)-u_{3}(t- \sigma)]. \end{cases}\displaystyle \end{aligned}$$

(62)

Clearly, system (62) has the equilibrium point $(0.9202,0.7667,-0.1534)$. One can easily verify that the conditions $({\mathcal{C}}_{1})$, $({\mathcal{C}}_{4})$, $({\mathcal{C}}_{5})$ of Theorem 4 are fulfilled. By virtue of computer, we can determine that $\varsigma_{0}=2.1165$, $\sigma_{\star}\approx0.04$. To verify the correctness of the main results of Theorem 4, we choose both time delay values. One is $\sigma=0.03$ and the other is $\sigma=0.6$. For $\sigma=0.03<\sigma_{\star}\approx0.04$, we get numerical simulation results which are presented in Fig. 6. In Fig. 6, we can see that $u_{1}\rightarrow0.9202$, $u_{2}\rightarrow0.7667$, $u_{2}\rightarrow-0.1534$ when $t\rightarrow+\infty$. That is to say, the equilibrium point $(0.9202,0.7667,-0.1534)$ of system (62) is locally asymptotically stable. For $\sigma=0.06>\sigma_{\star}\approx0.04$, we get numerical simulation results which are presented in Fig. 7. In Fig. 7, we can see that $u_{1}$ will keep periodic vibration around the value 0.9202, $u_{2}$ will keep periodic vibration around the value 0.7667 and $u_{2}$ will keep periodic vibration around the value −0.1534. That is to say, a Hopf bifurcation appears near the equilibrium point $(0.9202,0.7667,-0.1534)$. Moreover, the bifurcation plots, which clearly display the bifurcation value of system (62), are presented in Figs. 8–10. In Figs. 8–10, we can see that the bifurcation value of system (62) $\sigma_{0}\approx0.04$.

Figure 6

Computer simulation figures of system (62) with $\sigma=0.03<\sigma_{0}\approx0.04$. The equilibrium point $(0.9202,0.7667,-0.1534)$ is locally asymptotically stable state.

Figure 7

Computer simulation figures of system (62) with $\sigma=0.06>\sigma_{\star}\approx0.04$. A Hopf bifurcation takes place around the equilibrium point $(0.9202,0.7667,-0.1534)$.

Figure 8

Bifurcation diagram of system (62): t-$u_{1}$. The bifurcation value $\sigma_{\star}\approx0.04$.

Figure 9

Bifurcation diagram of system (62): t-$u_{2}$. The bifurcation value $\sigma_{\star}\approx0.04$.

Figure 10

Bifurcation diagram of system (62): t-$u_{3}$. The bifurcation value $\sigma_{\star}\approx0.04$.

Remark 7

In system (61), we obtain the bifurcation value $\sigma_{0}\approx0.08$. In system (62), we obtain bifurcation value $\sigma_{\star}\approx0.04$. We can easily see that the stability region of system (61) is narrowed and the time of onset of Hopf bifurcation of system (61) is advanced.

6 Conclusions

In recent years, the investigation on financial models or economic models has attracted much interest from mathematical and financial circles. Mathematically speaking, revealing the effect of time delay on the dynamics of financial models or economic models has become a vital topic. In this article, we build a new delayed finance model. The existence, uniqueness, and boundedness of solution to the established delayed finance model are analyzed in detail. By selecting the time delay as bifurcation parameter, we derive a delay-independent condition guaranteeing the stability and creation of Hopf bifurcation of the established delayed finance model. By designing a suitable hybrid controller that includes state feedback and parameter perturbation, we can efficaciously control the stability region and the time of occurrence of Hopf bifurcation of the established delayed finance model. The results derived from this article have important theoretical significance in managing economic operation for some related economic sectors. We can effectively control the the interest rate, the investment demand and the price index in finance via adjusting the delay. Also, the study idea can be applied to explore the bifurcation control issue of lots of other differential systems. In this paper, we controlled the Hopf bifurcation via hybrid control strategy. Of course, we can control Hopf bifurcation of model (5) via other hybrid control strategies. We will explore this aspect in near future.