Existence theory for multiple solutions to second-order singular Dirichlet boundary value problem modeling the Antarctic Circumpolar Current

Abstract

In the article, we present multiple solutions for a second-order singular Dirichlet boundary value problem that arises when modeling the ocean flow of the Antarctic Circumpolar Current. The main tools of the proof are the Leray–Schauder nonlinear alternative principle and a well-known fixed point theorem in cones.

1 Introduction

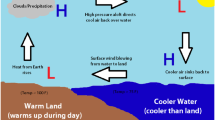
Gyres are known as the circulation of ocean flows derived by the combination of gravity and Coriolis forces produced by the Earth’s rotation. To balance the two forces against each other, the ocean flows adjust to the two forces acting primarily on them [18, 19]. Especially, the Antarctic Circumpolar Current (ACC) plays an extremely key role in global climate among the ocean flows. It is the main way of exchanging water between the Pacific, Indian, and Atlantic oceans.

Recently, the existence of solutions to geophysical fluid dynamics nonlinear governing equations, proposed by Constantin et al. [10–16], has been widely discussed and studied in this field. In practice, these geophysical flows have horizontal velocities with about a factor 10⁴ larger than the vertical velocities [32]. Therefore, on a rotating sphere, a stream function can be introduced to model gyres as shallow water flows by neglecting vertical velocities in [16]. In spherical coordinates, the model can be transformed into a planar elliptic partial differential equation under the stereographic projection. By ignoring the change of azimuth variation, Chu first transformed the arctic gyres model (i.e., elliptic partial differential equation) into a second-order differential equation by seeking a radially symmetric solution in [2]. The existence and some explicit solutions of non-trivial solutions in the case of constant vorticity and linear vorticity functions were presented. After that, a series of works [3–5] were devoted to studying this problem with nonlinear vorticity functions and different kinds of boundary value conditions. Marynets and Haziot also considered such equations about the Antarctic Circumpolar Current with suitable boundary conditions in reference [20, 21, 25–29]. In what follows, we first review the model of the general motion of a gyre flow in spherical coordinates. Let $\varphi \in [0,2\pi )$ be the azimuthal angle (i.e., the angle of longitude) and $\theta \in [0,\pi )$ be the polar angle, $\theta =0$ corresponds to the North Pole. On the spherical Earth, the azimuthal and velocity components of the horizontal gyre flow are respectively given by

$$\begin{aligned} \frac{1}{\sin \theta}\psi _{\varphi} \quad\text{and} \quad -\psi _{\theta}, \end{aligned}$$

where $\psi (\theta ,\varphi )$ is the stream function. See [16], recording

$$\begin{aligned} \Psi (\theta ,\varphi )=\psi (\theta ,\varphi )+\omega \cos \theta , \end{aligned}$$

(1.1)

where Ψ is the stream function related to the ocean’s motion. The governing equation for the gyres is

$$\begin{aligned} \frac{1}{\sin ^{2}\theta}\Psi _{\varphi \varphi}+\Psi _{\theta}\cot \theta +\Psi _{\theta \theta}=F(\Psi -\omega \cos \theta ), \end{aligned}$$

(1.2)

where $\omega >0$ is the non-dimensional Coriolis parameter, $2\omega \cos \theta$ is the planetary vorticity generated by Earth’s rotation, $F(\Psi -\omega \cos \theta )$ is the ocean vorticity. The total vorticity of the ocean flow equals the sum of $2\omega \cos \theta$ and $F(\Psi -\omega \cos \theta )$.

Let $(r, \phi )$ be the polar coordinates in the equatorial plane. By making a stereographic projection of the unit sphere from the North Pole to the equatorial plane

$$\begin{aligned} \xi =re^{i\phi}\quad \text{with } r=\cot \biggl(\frac{\theta}{2} \biggr)= \frac{\sin \theta}{1-\cos \theta}, \end{aligned}$$

(1.3)

we have

$$\begin{aligned} \cos \theta =\frac{\xi \bar{\xi}-1}{\xi \bar{\xi}+1},\qquad \sin \theta =\frac{2\sqrt{\xi \bar{\xi}}}{\xi \bar{\xi}+1}, \qquad\partial _{\theta}=-\frac{\xi}{\sin \theta}\partial _{\xi}- \frac{\bar{\xi}}{\sin \theta} \partial _{\bar{\xi}}, \qquad\partial _{\phi}={i}\xi \partial _{\xi}-{i}\bar{\xi}\partial _{ \bar{\xi}}. \end{aligned}$$

Using (1.3) to cancel several terms, we obtain that equation (1.2) can be simplified as

$$\begin{aligned} \Psi _{\xi \bar{\xi}}= \frac{F(\Psi -\omega ((\xi \bar{\xi}-1)/(\xi \bar{\xi}+1)))}{(1+\xi \bar{\xi})^{2}}. \end{aligned}$$

(1.4)

By computing partial derivatives in (1.1), we have

$$\begin{aligned} \Psi _{\xi}=\psi _{\xi}+ \frac{2\omega \bar{\xi}}{(1+\xi \bar{\xi})^{2}},\qquad \Psi _{\xi \bar{\xi}}=\psi _{\xi \bar{\xi}}+ \frac{2\omega}{(1+\xi \bar{\xi})^{2}}- \frac{4\omega \xi \bar{\xi}}{(1+\xi \bar{\xi})^{3}}. \end{aligned}$$

(1.5)

Together (1.5) with (1.4), we get

$$\begin{aligned} \psi _{\xi \bar{\xi}}+2\omega \frac{1-\xi \bar{\xi}}{(1+\xi \bar{\xi})^{3}}- \frac{F(\psi )}{(1+\xi \bar{\xi})^{2}}=0. \end{aligned}$$

According to Cartesian coordinates $(x,y)$, the gyre flow model (1.2) can be transformed into the elliptic partial differential equation

$$\begin{aligned} \Delta \psi +8\omega \frac{1-(x^{2}+y^{2})}{(1+x^{2}+y^{2})^{3}}- \frac{4F(\psi )}{(1+x^{2}+y^{2})^{2}}=0, \end{aligned}$$

(1.6)

where $\Delta =\partial ^{2}_{x}+\partial ^{2}_{y}$ is the Laplace operator, represented by the Cartesian coordinates on the equatorial plane, and the unknown function $\psi (x,y)$ expresses the stream function.

Since ACC is one of the most important ocean currents with considerable uniformity in the azimuthal direction (see the discussions in [14, 33]). Therefore, we can furtherly simplify problem (1.2).

From

$$\begin{aligned} r=\sqrt{x^{2}+y^{2}},\qquad \frac{\partial r}{\partial x}=\frac{x}{\sqrt{x^{2}+y^{2}}}= \frac{x}{r}, \qquad\frac{\partial r}{\partial y}=\frac{y}{\sqrt{x^{2}+y^{2}}}= \frac{y}{r}, \end{aligned}$$

we obtain

$$\begin{aligned} &\psi _{x}=\frac{x}{r}\dot{\psi}(r)\quad \text{and}\quad \psi _{y}=\frac{y}{r}\dot{\psi}(r),\\ &\psi _{xx}=\frac{y^{2}}{r^{3}}\dot{\psi}(r)+\frac{x^{2}}{r^{2}} \ddot{ \psi}(r) \quad\text{and}\quad \psi _{yy}=\frac{x^{2}}{r^{3}}\dot{\psi}(r)+ \frac{y^{2}}{r^{2}} \ddot{\psi}(r), \end{aligned}$$

therefore

$$\begin{aligned} \Delta \psi =\ddot{\psi}(r)+\frac{1}{r}\dot{\psi}(r). \end{aligned}$$

Thus, linking with (1.6), we have

$$\begin{aligned} \ddot{\psi}(r)+\frac{1}{r}\dot{\psi}(r)+8\omega \frac{1-r^{2}}{(1+r^{2})^{3}} -\frac{4F(\psi (r))}{(1+r^{2})^{2}}=0. \end{aligned}$$

(1.7)

Actually, when the gyre flow has no variation in the azimuthal direction, we can look for a radial symmetric solutions $\psi =\psi (r)$ of problem (1.7).

Using the change of variables

$$\begin{aligned} \psi (r)=U(s), \quad s_{1}< s< s_{2} \end{aligned}$$

with $r=e^{-s/2}$ for

$$\begin{aligned} 0< s_{1}=-2\ln (r_{+})< s< s_{2}=-2\ln (r_{-}) \end{aligned}$$

and $0< r_{-}< r_{+}<1$,

we obtain

$$\begin{aligned} \dot{U}(s)=-\frac{1}{2}e^{-s/2}\dot{\psi}\bigl(e^{-s/2} \bigr)=-\frac{1}{2}r \dot{\psi}(r) \end{aligned}$$

and

$$\begin{aligned} \ddot{U}(s)=\frac{1}{4}e^{-s/2}\dot{\psi}\bigl(e^{-s/2} \bigr)+\frac{1}{4}e^{-s} \ddot{\psi}\bigl(e^{-s/2}\bigr) = \frac{1}{4}r\dot{\psi}(r)+\frac{1}{4}r^{2} \ddot{\psi}(r). \end{aligned}$$

Then equation (1.7) is transformed into the second-order ordinary differential equation

$$\begin{aligned} \ddot{U}(s)-\frac{e^{s}}{(1+e^{s})^{2}}F\bigl(U(s)\bigr)+ \frac{2\omega e^{s}(e^{s}-1)}{(1+e^{s})^{3}}=0,\quad s_{1}< s< s_{2}. \end{aligned}$$

(1.8)

In the newest literature [7, 17, 34–36, 38], many functional-analytic techniques were used to research the solutions of this second-order differential equation (1.8) with large classes of functions for the nonlinear functions F, such as the lower and upper solutions, theory of topological degree and so on. But when the nonlinear functions F may be singular at $U=0$, it is rarely discussed as far as we know. In the present paper, we will consider this situation for the Antarctic Circumpolar Current.

Between parallels of latitude defined by an appropriate choice of $r_{\pm}\in (0,1)$ with $r_{+}/r_{-}\in (1,2)$, the flow in a jet component of the ACC is described by equation (1.8) and the following boundary conditions

$$\begin{aligned} U(s_{1})=U(s_{2})=0, \end{aligned}$$

(1.9)

which means the boundary of the jet is a streamline, which confines a particle because the flow is steady.

For $0< s_{1}< s_{2}$, using the change of variables

$$\begin{aligned} u(t)=U(s),\quad t=\frac{s-s_{1}}{s_{2}-s_{1}}, \end{aligned}$$

the second-order boundary value problem (1.8)–(1.9) can be transformed into the following two-point boundary value problem

$$\begin{aligned} \textstyle\begin{cases} \ddot{u}-\alpha (t)F(u(t))+\beta (t)=0,\quad 0< t< 1, \\ u(0)=u(1)=0,\end{cases}\displaystyle \end{aligned}$$

(1.10)

where

$$\begin{aligned} \alpha (t)= \frac{(s_{2}-s_{1})^{2}e^{(s_{2}-s_{1})t+s_{1}}}{(1+e^{(s_{2}-s_{1})t+s_{1}})^{2}}= \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}>0 \end{aligned}$$

(1.11)

and

$$\begin{aligned} \beta (t) &= \frac{2\omega (s_{2}-s_{1})^{2}e^{(s_{2}-s_{1})t+s_{1}}(e^{(s_{2}-s_{1})t+s_{1}}-1)}{(1+e^{(s_{2}-s_{1})t+s_{1}})^{3}} \\ &= \frac{\omega (s_{2}-s_{1})^{2}\sinh (\frac{(s_{2}-s_{1})t+s_{1}}{2})}{2\cosh ^{3}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}>0. \end{aligned}$$

(1.12)

Due to the element inequality and the above conditions, we can easily know that the numerical range of $\alpha (t)$ is $\alpha (t)\in [ { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{s_{2}}{2})}}, { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{s_{1}}{2})}} ] \subseteq (0,(\ln 2)^{2})$.

In the present paper, we are especially interested in the nonlinear vorticity function $F(u)$ with attractive singularity in the dependent variable $u=0$, i.e., $\lim_{u\rightarrow 0_{+}}F(u)=-\infty$, which means that problem (1.10) is a singular boundary value problem. The study of singular boundary value problems has come from many applications since the middle 1970s. In 1979, Taliaferro [31] established that the singular boundary value problem

$$\begin{aligned} \textstyle\begin{cases} \ddot{y}+q(t)y^{-a}=0, \quad 0< t< 1, \\ y(0)=y(1)=0,\end{cases}\displaystyle \end{aligned}$$

has a solution $y(t)\in C[0, 1]\cap C^{1}(0, 1)$; here $a>0, q\in C(0, 1)$ with $q>0$ on $(0, 1)$ and $\int ^{1}_{0}t(1-t) q(t) \,dt <\infty$. This generated the interest of many researchers in singular problems frequently arising in the study of nonlinear phenomena. In the 1980s and 1990s, many scholars studied the singular boundary value problems:

$$\begin{aligned} \textstyle\begin{cases} \ddot{y}+q(t)f(t,y)=0,\quad 0< t< 1, \\ y(0)=y(1)=0.\end{cases}\displaystyle \end{aligned}$$

(1.13)

Agarwal and O’Regan discussed the existence and multiplicity of solutions to singular positive boundary value problems (1.13) in [1]. They used the Leray–Schauder alternative principle and a well-known fixed point theorem in cones. Chu generalized the results to singular Dirichlet systems in [8]. There are also some other classical tools that have been used to discuss periodic singular differential equations in literature [6, 9, 22, 23]. In this paper, we adopt the ideas in [1, 8] to achieve multiple solutions for the second-order singular Dirichlet boundary value problem of Antarctic Circumpolar Current

$$\begin{aligned} \textstyle\begin{cases} \ddot{u}+\alpha (t)(u^{-a}+\nu u^{b})+\beta (t)=0,\quad 0< t< 1, \\ u(0)=u(1)=0,\end{cases}\displaystyle \end{aligned}$$

(1.14)

where $\alpha (t)$, $\beta (t)$ are described as in (1.11) and (1.12), $a>0$, $b>0$, and $\nu \in {\mathbb{R}}$ is a given parameter.

In this paper, we use the notation ${\mathbb{R}}^{+}=[0,\infty )$ and ${\mathbb{R}}^{-}=(-\infty ,0]$. If $\phi \geq 0$ for all $t\in [0,1]$, and it is positive in a set of positive measure, we say that $\phi \succ 0$. We still use the supremum norm of ${\mathbb{C}}[0,1]$ with the norm $\|u\|=\sup_{t\in [0,1]}|u(t)|$.

The rest of the paper is organized as follows. In Sect. 2, several preliminary knowledge and theorems are given. In Sect. 3, we state and prove the existence results when the nonlinear oceanic vorticity F has an attractive singularity. Moreover, some applications of the new results to (1.10) are also presented in Sect. 3. A brief conclusion is given in Sect. 4.

2 Preliminaries and notation

Let us first review the following lemma and an existence principle in [1], which will be required in Sect. 3.

Lemma 2.1

([1])

Let

$$\begin{aligned} {\mathcal{K}}= \bigl\{ u\in {\mathbb{C}}[0,1]: u(t)\geq 0, t\in [0,1] \textit{ and } u(t) \textit{ is concave on } [0,1] \bigr\} . \end{aligned}$$

Then for all $u\in \mathcal{K}$,

$$\begin{aligned} u(t)\geq t(1-t) \Vert u \Vert ,\quad 0\leq t\leq 1. \end{aligned}$$

Consider the scalar problem

$$\begin{aligned} \textstyle\begin{cases} \ddot{u}+f(t,u)=0, \quad 0< t< 1, \\ u(0)=a, \qquad u(1)=b.\end{cases}\displaystyle \end{aligned}$$

(2.1)

Theorem 2.2

([1])

Suppose the following two conditions are satisfied:

• (1) the map $u\rightarrow f(t,u)$ is continuous for a.e. $0\leq t\leq 1$,

• (2) the map $t\rightarrow f(t,u)$ is measurable for all $u\in {\mathbb{R}}$.

  • (I) Assume for each $r>0$, there exists $h_{r}\in L^{1}_{\mathrm{loc}}(0,1)$ with ${\int _{0}^{1}}t(1-t)h_{r}(t)\,dt<\infty$ such that $\|u\|\leq r$ implies $|f(t,u)|\leq h_{r}(t)$ for a.e. $t\in (0,1)$ holds. In addition, suppose that there is a constant $M>|a|+|b|$, independent of λ, with

    $$\begin{aligned} \Vert u \Vert =\sup_{0\leq t\leq 1} \bigl\vert u(t) \bigr\vert \neq M \end{aligned}$$

    for any solution $u\in AC[0,1]$ (with $\dot{u}\in AC_{loc}(0,1)$) to

    $$\begin{aligned} \textstyle\begin{cases} \ddot{u}+\lambda f(t,u)=0, \quad 0< t< 1, \\ u(0)=a, \qquad u(1)=b,\end{cases}\displaystyle \end{aligned}$$

    for each $\lambda \in (0,1)$. Then (2.1) has a solution u with $\|u\|\leq M$.

  • (II) Assume that there exists $h\in L^{1}_{\mathrm{loc}}(0,1)$ with ${\int _{0}^{1}}t(1-t)h(t)\,dt<\infty$ such that $|f(t,u)|\leq h(t)$ for a.e. $t\in (0,1)$ and $u\in {\mathbb{R}}$. Then (2.1) has a solution.

Next we present the following two well-known results that will be applied to demonstrate our main results.

Theorem 2.3

(Leray–Schauder alternative principle [30])

Assume that Ω is an open subset of a convex set K in a normed linear space X, and $p\in \Omega$. Let $T:\overline{\Omega}\rightarrow K$ be a compact continuous map. Then one of the following two conclusions holds:

• (I) T has at least one fixed point in Ω̅.

• (II) There exists $u\in \partial \Omega$ and $0<\lambda <1$ such that $u=\lambda Tu+(1-\lambda )p$.

Let K be a cone in X and D be a subset of X. We write $\partial _{K}D=(\partial D)\cap K$ and $D_{K}=D\cap K$.

Theorem 2.4

([24])

Let X be a Banach space, and let K be a cone in X. Assume that $\Omega ^{1}$, $\Omega ^{2}$ are open bounded subsets of X with $\Omega ^{1}_{K}\neq \emptyset$, $\overline{\Omega}^{1}_{K}\subset \Omega ^{2}_{K}$. Let

$$\begin{aligned} S:\overline{\Omega}^{2}_{K}\rightarrow K \end{aligned}$$

be a continuous and completely continuous operator such that

• (i) $u\neq \lambda Su$ for $\lambda \in [0,1)$ and $u\in \partial _{K}\Omega ^{1}$, and

• (ii) there exists $v\in K\backslash \{0\}$ such that $u\neq Su+\lambda v$ for all $u\in \partial _{K}\Omega ^{2}$ and all $\lambda >0$.

Then S has a fixed point in $\overline{\Omega}^{2}_{K}\backslash \Omega ^{1}_{K}$.

In the present paper, we research the second-order singular Dirichlet boundary value problem (1.10). Throughout this paper, we suppose that $F:[0,1] \times {\mathbb{R}}^{+}\backslash \{0\}\rightarrow {\mathbb{R}}^{-}$ is the continuous oceanic vorticity function and $\lim_{u\rightarrow 0_{+}}F(t,u)=-\infty$.

Due to

$$\begin{aligned} \int ^{1}_{0}t(1-t)\beta (t)\,dt &= \int ^{1}_{0}t(1-t) \cdot \frac{\omega (s_{2}-s_{1})^{2}\sinh (\frac{(s_{2}-s_{1})t+s_{1}}{2})}{2\cosh ^{3}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}\,dt \\ &\le \frac{1}{4}\omega (s_{2}-s_{1})^{2} { \int _{0}^{1}} \frac{\sinh (\frac{(s_{2}-s_{1})t+s_{1}}{2})}{2\cosh ^{3}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}\,dt \\ &= \frac{1}{4}\omega (s_{2}-s_{1}) { \int _{0}^{1}} \frac{d[\cosh (\frac{(s_{2}-s_{1})t+s_{1}}{2})]}{\cosh ^{3}(\frac{(s_{2}-s_{1})t+s_{1}}{2})} \\ &= -\frac{1}{8}\omega (s_{2}-s_{1})\cosh ^{-2} \biggl( \frac{(s_{2}-s_{1})t+s_{1}}{2} \biggr)\bigg|_{0}^{1} \\ &= -\frac{1}{8}\omega (s_{2}-s_{1}) \biggl( \frac{1}{\cosh ^{2}(\frac{s_{2}}{2})}- \frac{1}{\cosh ^{2}(\frac{s_{1}}{2})}\biggr) \\ &< +\infty . \end{aligned}$$

Using Theorem 2.2(II), we know that the following problem

$$\begin{aligned} \textstyle\begin{cases} \ddot{u}+ { \frac{\omega (s_{2}-s_{1})^{2}\sinh (\frac{(s_{2}-s_{1})t+s_{1}}{2})}{2\cosh ^{3}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}}=0,\quad 0< t< 1, \\ u(0)=0, \qquad u(1)=0,\end{cases}\displaystyle \end{aligned}$$

has a solution μ. Factually, $\mu :{\mathbb{R}}\rightarrow {\mathbb{R}}^{+}$ can be expressed as

$$\begin{aligned} \mu (t)= { \int _{0}^{1}}G(t,\tau )\cdot { \frac{\omega (s_{2}-s_{1})^{2}\sinh (\frac{(s_{2}-s_{1})\tau +s_{1}}{2})}{2\cosh ^{3}(\frac{(s_{2}-s_{1})\tau +s_{1}}{2})}} \,d \tau , \end{aligned}$$

where

$$\begin{aligned} G(t,s)=\textstyle\begin{cases} t(1-s), & 0\leq t\leq s\leq 1, \\ s(1-t), & 0\leq s\leq t\leq 1,\end{cases}\displaystyle \end{aligned}$$

is the Green function for

$$\begin{aligned} \textstyle\begin{cases} \ddot{u}=0,\quad 0< t< 1, \\ u(0)=0, \qquad u(1)=0.\end{cases}\displaystyle \end{aligned}$$

Since $G(t,s)\geq 0$ and $\beta (t)= { \frac{\omega (s_{2}-s_{1})^{2}\sinh (\frac{(s_{2}-s_{1})t+s_{1}}{2})}{2\cosh ^{3}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}}>0$, we can easily know that $\mu (t)\geq 0$.

In this paper, we denote

$$\begin{aligned} \mu _{\ast}=\min_{t}\mu (t),\qquad \mu ^{\ast}= \max_{t} \mu (t), \end{aligned}$$

we can easily know $\mu _{\ast}\geq 0$.

To conclude the preliminaries, we observe that if the singular Dirichlet boundary value problem

$$\begin{aligned} \textstyle\begin{cases} \ddot{u}- { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}}F(t,u(t)+ \mu (t))=0, \quad 0< t< 1, \\ u(0)=0,\qquad u(1)=0,\end{cases}\displaystyle \end{aligned}$$

(2.2)

has a nonnegative solution u satisfying $u(t)+\mu (t)>0$ for $t\in (0,1)$ and $0<\|u\|<r$, we can calculate the system to get

$$\begin{aligned} \ddot{u}+\ddot{\mu}- { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}}F\bigl(t,u(t)+ \mu (t)\bigr) + { \frac{\omega (s_{2}-s_{1})^{2}\sinh (\frac{(s_{2}-s_{1})t+s_{1}}{2})}{2\cosh ^{3}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}}=0, \end{aligned}$$

that is, $y(t)=u(t)+\mu (t)$ is a nonnegative solution of (1.10) with $0<\|y-\mu \|<r$. Therefore, for the convenience, we will consider (2.2) in the next section.

3 Main results

Define an operator ${\mathcal{A}}: X \rightarrow X$ by

$$\begin{aligned} ({\mathcal{A}}u) (t)=- \int _{0}^{1} \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})s+s_{1}}{2})}F\bigl(s,u(s)+ \mu (s)\bigr)G(t,s)\,ds. \end{aligned}$$

It is well known that seeking a solution of (2.2) is equivalent to seeking a fixed point for the operator ${\mathcal{A}}$.

Theorem 3.1

Assume that three conditions are satisfied:

$\mathrm{(H_{1})}$:

For each positive constant L, there is a continuous function $\phi _{L}\succ 0$ satisfying

$$\begin{aligned} F(t,u)\leq -\phi _{L}(t) \end{aligned}$$

for $(t,u)\in (0,1) \times (0,L]$;

$\mathrm{(H_{2})}$:

there exist two nonnegative continuous functions $g(u)$ and $h(u)$ on $(0,\infty )$ satisfying

$$\begin{aligned} -g(u)-h(u)\leq F(t,u)\leq 0 \end{aligned}$$

for $(t,u)\in (0,1) \times (0,\infty )$, where $g(u)$ is non-increasing, and $h(u)/g(u)$ is non-decreasing in u;

$\mathrm{(H_{3})}$:

there exists a constant $r>0$ satisfying:

$$\begin{aligned} {\frac{(s_{2}-s_{1})^{2}}{24\cosh ^{2}(\frac{s_{1}}{2})}} \biggl\{ 1+ {\frac{h(r+\mu ^{\ast})}{g(r+\mu ^{\ast})}} \biggr\} < { \int _{0}^{r}}\frac{1}{g(u)}\,du \end{aligned}$$

Then (1.10) has at least a nonnegative solution $u\in C[0,1]\cap C^{2}(0,1)$ with $u(t)>0$ for all $t\in (0,1)$ and $0<\|u-\mu \|<r$.

Proof

From the end of Sect. 2, it is enough if we find that (2.2) has a nonnegative solution u such that $0<\|u\|<r$ and $u(t)+\mu (t)>0$ for $t\in (0,1)$.

Since ${\mathrm{(H_{3})}}$ holds, we choose a positive constant $\varepsilon >0$ and $\varepsilon < r$, satisfying

$$\begin{aligned} {\frac{(s_{2}-s_{1})^{2}}{24\cosh ^{2}(\frac{s_{1}}{2})}} \biggl\{ 1+ {\frac{h(r+\mu ^{\ast})}{g(r+\mu ^{\ast})}} \biggr\} < { \int _{\varepsilon}^{r}}\frac{1}{g(u)} \,du. \end{aligned}$$

(3.1)

Choosing $n_{0}$ from $\{1,2,\ldots \}$ satisfying $\frac{1}{n_{0}}<\frac{\varepsilon}{2}$. Let $N_{0}=\{n_{0},n_{0}+1,\ldots \}$. We will consider the family of problems

$$\begin{aligned} \textstyle\begin{cases} \ddot{u}-\lambda { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}}F^{m}(t,u(t)+ \mu (t))=0, & 0< t< 1, \\ u(0)=u(1)=\frac{1}{m},& m\in N_{0},\end{cases}\displaystyle \end{aligned}$$

(3.2)

where $\lambda \in [0,1]$ and

$$\begin{aligned} F^{m}(t,u)=\textstyle\begin{cases} F(t,u) ,& u\geq \frac{1}{m}, \\ F(t,\frac{1}{m}) ,& u\leq \frac{1}{m}.\end{cases}\displaystyle \end{aligned}$$

Define the operator ${\mathcal{A}}^{m}:X\rightarrow X$:

$$\begin{aligned} \bigl({\mathcal{A}}^{m}u\bigr) (t)= { \int _{0}^{1}G(t,\tau ) \biggl[- { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})\tau +s_{1}}{2})}} F^{m}\bigl(\tau ,u(\tau )+\mu (\tau )\bigr) \biggr] \,d\tau}. \end{aligned}$$

Then the solution of (3.2) is found if the following fixed point problem

$$\begin{aligned} u=\lambda {\mathcal{A}}^{m}u+\frac{1}{m} \end{aligned}$$

(3.3)

is solved.

In what follows, we will declare that any fixed point u of (3.3) must satisfy $\|u\|\neq r$ for any $\lambda \in [0,1]$. Otherwise, assume that u is a fixed point of (3.3) for some $\lambda \in [0,1]$ with $\|u\| =r$. Notice that since $\alpha (t)= { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}}>0$ and $F^{m}(t,u)\leq 0$, we have

$$\begin{aligned} \ddot{u}(t)=\lambda { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}}F^{m}\bigl(t,u(t)+ \mu (t) \bigr)\leq 0,\quad 0\leq t\leq 1 \end{aligned}$$

and $u(t)\geq \frac{1}{m}>0$ for $0\leq t\leq 1$. Therefore, by Lemma 2.1

$$\begin{aligned} u(t)\geq t(1-t) \Vert u \Vert . \end{aligned}$$

Therefore, there exists $t_{m}\in (0,1)$ with $\dot{u}(t)\geq 0$ on $(0,t_{m})$, $\dot{u}(t)\leq 0$ on $(t_{m},1)$ and $u(t_{m})=\|u\|=r$. Then for $\tau \in (0,1)$, according to ${\mathrm{(H_{2})}}$ and $F(t,u)\leq 0$, we have

$$\begin{aligned} \ddot{u}(\tau ) &= \lambda { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})\tau +s_{1}}{2})}}F^{m}\bigl( \tau ,u(\tau )+\mu (\tau )\bigr) \\ &= \lambda { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})\tau +s_{1}}{2})}}F\bigl( \tau ,u(\tau )+\mu (\tau )\bigr) \\ &\ge { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})\tau +s_{1}}{2})}}\bigl[-g\bigl(u( \tau )+\mu (\tau )\bigr)-h\bigl(u( \tau )+\mu (\tau )\bigr)\bigr] \\ &\ge - { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{s_{1}}{2})}}g\bigl(u(\tau )+ \mu (\tau )\bigr) \biggl\{ 1+ \frac{h(u(\tau ) +\mu (\tau ))}{g(u(\tau )+\mu (\tau ))} \biggr\} . \end{aligned}$$

So

$$\begin{aligned} -\ddot{u}(\tau ) \leq { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{s_{1}}{2})}}g\bigl(u(\tau )+ \mu ( \tau )\bigr) \biggl\{ 1+ \frac{h(u(\tau ) +\mu (\tau ))}{g(u(\tau )+\mu (\tau ))} \biggr\} . \end{aligned}$$

(3.4)

Integrate (3.4) from $t_{m}$ to $t(t\geq t_{m})$ to obtain

$$\begin{aligned} -\dot{u}(t)\leq g\bigl(u(t)\bigr) \biggl\{ 1+ { \frac{h(r+\mu ^{\ast})}{g(r+\mu ^{\ast})}} \biggr\} { \int _{t_{m}}^{ t}} { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{s_{1}}{2})}}\,d\tau . \end{aligned}$$

(3.5)

Therefore, we have

$$\begin{aligned} -\frac{\dot{u}(t)}{g(u(t))}\leq \biggl\{ 1+ { \frac{h(r+\mu ^{\ast})}{g(r+\mu ^{\ast})}} \biggr\} { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{s_{1}}{2})}} { \int _{t_{m}}^{ t}}\,d\tau . \end{aligned}$$

(3.6)

Then integrating from $t_{m}$ to 1, we obtain

$$\begin{aligned} - { \int _{t_{m}}^{1}}\frac{\dot{u}(t)}{g(u(t))}\,dt \leq \biggl\{ 1+ {\frac{h(r+\mu ^{\ast})}{g(r+\mu ^{\ast})}} \biggr\} { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2} (\frac{s_{1}}{2})}} { \int _{t_{m}}^{1}} { \int _{t_{m}}^{ t}}\,d\tau \,dt. \end{aligned}$$

That is

$$\begin{aligned} { \int _{\frac{1}{m}}^{r}}\frac{du}{g(u)} \leq \biggl\{ 1+ { \frac{h(r+\mu ^{\ast})}{g(r+\mu ^{\ast})}} \biggr\} {\frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2} (\frac{s_{1}}{2})}} { \int _{t_{m}}^{1}}(1-\tau )\,d\tau . \end{aligned}$$

(3.7)

Consequently,

$$\begin{aligned} { \int _{\varepsilon}^{r}}\frac{du}{g(u)} &\le \biggl\{ 1+ {\frac{h(r+\mu ^{\ast})}{g(r+\mu ^{\ast})}} \biggr\} { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{s_{1}}{2})}} { \int _{t_{m}}^{1}}(1-\tau )\,d\tau \\ &\le \biggl\{ 1+ { \frac{h(r+\mu ^{\ast})}{g(r+\mu ^{\ast})}} \biggr\} { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2} (\frac{s_{1}}{2})}} \frac{1}{t_{m}} { \int _{t_{m}}^{1}} \tau (1-\tau )\,d\tau . \end{aligned}$$

(3.8)

Similarly, integrating (3.4) from $t(t\leq t_{m})$ to $t_{m}$ and then from 0 to $t_{m}$, we can obtain

$$\begin{aligned} { \int _{\varepsilon}^{r}}\frac{du}{g(u)}\leq \biggl\{ 1+ { \frac{h(r+\mu ^{\ast})}{g(r+\mu ^{\ast})}} \biggr\} {\frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{s_{1}}{2})}} \frac{1}{1-t_{m}} { \int _{0}^{t_{m}}}\tau (1-\tau )\,d\tau . \end{aligned}$$

(3.9)

When $0< t_{m}\leq \frac{1}{2}$, we have

$$\begin{aligned} \frac{1}{1-t_{m}} { \int _{0}^{t_{m}}}\tau (1-\tau )\,d\tau \leq 2 { \int _{0}^{\frac{1}{2}}}\tau (1-\tau )\,d\tau = { \frac{1}{6}}. \end{aligned}$$

When $\frac{1}{2}\leq t_{m}<1$, we have

$$\begin{aligned} \frac{1}{t_{m}} { \int _{t_{m}}^{1}}\tau (1-\tau )\,d\tau \leq 2 { \int _{\frac{1}{2}}^{1}}\tau (1-\tau )\,d\tau = { \frac{1}{6}}. \end{aligned}$$

Therefore, (3.8) and (3.9) imply

$$\begin{aligned} { \int _{\varepsilon}^{r}}\frac{du}{g(u)}\leq { \frac{(s_{2}-s_{1})^{2}}{24\cosh ^{2}(\frac{s_{1}}{2})}} \biggl\{ 1+ {\frac{h(r+\mu ^{\ast})}{g(r+\mu ^{\ast})}} \biggr\} . \end{aligned}$$

This contradicts with (3.1), which implies $\|u\|\neq r$. Therefore, Theorem 2.2 ensures that

$$\begin{aligned} u=\lambda {\mathcal{A}}^{m}u+\frac{1}{m} \end{aligned}$$

has a fixed point record as $u_{m}$. That is, the system

$$\begin{aligned} \textstyle\begin{cases} \ddot{u}- { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}}F^{m}(t,u(t)+ \mu (t))=0,& 0< t< 1, \\ u(0)=u(1)=\frac{1}{m},& m\in N_{0},\end{cases}\displaystyle \end{aligned}$$

(3.10)

has a solution record as $u_{m}$ satisfying $\|u_{m}\|\leq r$. Factually (as above)

$$\begin{aligned} \frac{1}{m}\leq u_{m}(t)< r \quad\text{for } t\in [0,1]. \end{aligned}$$

$u_{m}$ is certainly a positive solution of (3.10).

Following we will show that $u_{m}(t)+\mu (t)$ have a uniform sharper lower bound for all $m\in N_{0}$, that is, there exists a positive constant k independent of m satisfying

$$\begin{aligned} u_{m}(t)+\mu (t)\geq kt(1-t) \quad\text{for } t\in [0,1]. \end{aligned}$$

(3.11)

Due to $\mu _{\ast}\geq 0$, (3.11) is satisfied if we can establish that

$$\begin{aligned} u_{m}(t)\geq kt(1-t) \quad\text{for } t\in [0,1]. \end{aligned}$$

(3.12)

According to assumption ${\mathrm{(H_{1})}}$, there exists a continuous function $\phi _{r+\mu ^{\ast}}\succ 0$ satisfying $F(t,u)\leq -\phi _{r+\mu ^{\ast}}(t)$ for all $t\in (0,1)$ and $\|u\|\leq r+\mu ^{\ast}$. Let $u_{m}^{r+\mu ^{\ast}}$ be the unique solution of (3.10). Using the Green function, the solution of (3.10) can be represented as

$$\begin{aligned} u_{m}^{r+\mu ^{\ast}}(t) = {}& \frac{1}{m}+t { \int _{t}^{1}}(1-\tau ) \biggl[- { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})\tau +s_{1}}{2})}}F\bigl( \tau ,u_{m}(\tau )+\mu (\tau )\bigr) \biggr] \,d\tau \\ &{} +(1-t) { \int _{0}^{t}}\tau \biggl[- { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})\tau +s_{1}}{2})}}F \bigl( \tau ,u_{m}(\tau )+\mu (\tau )\bigr) \biggr]\,d\tau . \end{aligned}$$

Therefore, we have

$$\begin{aligned} u_{m}^{r+\mu ^{\ast}}(t) &\ge { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{s_{2}}{2})}} \biggl[t { \int _{t}^{1}}(1-\tau )\phi _{r+\mu ^{\ast}}(\tau ) \,d \tau +(1-t) { \int _{0}^{t}}\tau \phi _{r+\mu ^{\ast}}( \tau )\,d \tau \biggr] \\ &\equiv { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{s_{2}}{2})}}\Psi ^{r+\mu ^{ \ast}}(t). \end{aligned}$$

Now it is easy to calculate that

$$\begin{aligned} \dot{\Psi}^{r+\mu ^{\ast}}(t)= { \int _{t}^{1}}(1-\tau ) \phi _{r+\mu ^{\ast}}(\tau ) \,d\tau - { \int _{0}^{t}}\tau \phi _{r+\mu ^{\ast}}(\tau )\,d \tau\quad \text{for } t\in (0,1) \end{aligned}$$

with $\Psi ^{r+\mu ^{\ast}}(0)=\Psi ^{r+\mu ^{\ast}}(1)=0$. If $k_{0}\equiv {\int _{0}^{1}}(1-\tau )\phi _{r+\mu ^{\ast}}( \tau )\,d\tau$ exists, then $\dot{\Psi}^{r+\mu ^{\ast}}(0)=k_{0}$; otherwise, $\dot{\Psi}^{r+\mu ^{\ast}}(0)=\infty$. In either situation, there exists a constant $k_{1}>0$, independent of m, with $\dot{\Psi}^{r+\mu ^{\ast}}(0)\geq k_{1}$. Thus, there is an $\varepsilon >0$ with $\Psi ^{r+\mu ^{\ast}}(t)\geq \frac{1}{2}k_{1}t\geq \frac{1}{2}k_{1}t(1-t)$ for all $t\in [0,\varepsilon ]$. Similarly, there exists a constant $k_{2}$, independent of m, with $-\dot{\Psi}^{r+\mu ^{\ast}}(1)\geq k_{2}$. Thus, there is a $\delta >0$ with $\Psi ^{r+\mu ^{\ast}}(t)\geq \frac{1}{2}k_{2}(1-t)\geq \frac{1}{2}k_{2}t(1-t)$ for $t\in [1-\delta ,1]$.

Finally, for $t\in [\varepsilon ,1-\delta ]$, it is easy to check that

$$\begin{aligned} \frac{\Psi ^{r+\mu ^{\ast}}(t)}{t(1-t)} \quad\text{is continuous on } [ \varepsilon ,1-\delta ]. \end{aligned}$$

Then there exists a constant $k_{3}$, independent of m, with $\Psi ^{r+\mu ^{\ast}}(t)\geq \frac{1}{2}k_{3}t(1-t)$. Let us choose a positive constant $k=\min \{\frac{1}{2}k_{1},\frac{1}{2}k_{2},\frac{1}{2}k_{3}\}$, then (3.12) is true.

Furtherly, we will prove

$$\begin{aligned} \{u_{m}\}_{m\in N_{0}}\quad \text{is a bounded and equicontinuous family on } [0, 1]. \end{aligned}$$

(3.13)

Returning to (3.6) (with u replaced by $u_{m}$), we have

$$\begin{aligned} -\frac{\dot{u}_{m}(t)}{g(u_{m}(t))}\leq \biggl\{ 1+ { \frac{h(r+\mu ^{\ast})}{g(r+\mu ^{\ast})}} \biggr\} { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{s_{1}}{2})}}(t-t_{m}). \end{aligned}$$

(3.14)

On the other hand, we obtain

$$\begin{aligned} \frac{\dot{u}_{m}(t)}{g(u_{m}(t))}\leq \biggl\{ 1+ { \frac{h(r+\mu ^{\ast})}{g(r+\mu ^{\ast})}} \biggr\} { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{s_{1}}{2})}}(t_{m}-t). \end{aligned}$$

(3.15)

Consequently,

$$\begin{aligned} \frac{ \vert \dot{u}_{m}(t) \vert }{g(u_{m}(t))}\leq \biggl\{ 1+ { \frac{h(r+\mu ^{\ast})}{g(r+\mu ^{\ast})}} \biggr\} { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{s_{1}}{2})}} \vert t-t_{m} \vert . \end{aligned}$$

(3.16)

We now declare that there exist $c_{0}$ and $c_{1}$ with $c_{0}>0$, $c_{1}<1$, $c_{0}< c_{1}$ such that

$$\begin{aligned} c_{0}< \inf \{t_{m}:m\in N_{0}\} \leq \sup \{t_{m}:m\in N_{0}\}< c_{1}. \end{aligned}$$

(3.17)

Factually, it is enough if we can show that $\inf \{t_{m}:m\in N_{0}\}>0$ and $\sup \{t_{m}:m\in N_{0}\}<1$. First, we prove $\sup \{t_{m}:m\in N_{0}\}<1$. If this is false, there exists a subsequence S of $N_{0}$ with $t_{m}\rightarrow 1$ as $m\rightarrow \infty$ in S. Integrating (3.14) from $t_{m}$ to 1, we have

$$\begin{aligned} - { \int _{u_{m}(t_{m})}^{\frac{1}{m}}}\frac{dx}{g(x)} \leq \biggl\{ 1+ { \frac{h(r+\mu ^{\ast})}{g(r+\mu ^{\ast})}} \biggr\} { \frac{(s_{2}-s_{1})^{2}}{8\cosh ^{2}(\frac{s_{1}}{2})}}(1-t_{m})^{2} \end{aligned}$$

for $m\in S$. Since $t_{m}\rightarrow 1$ as $m\rightarrow \infty$ in S, we have from the inequality that $u_{m}(t_{m})\rightarrow 0$ as $m\rightarrow \infty$ in S. However, since the maximum of $u_{m}$ on $[0,1]$ occurs at $t_{m}$, we have $u_{m}\rightarrow 0$ in $C[0,1]$ as $m\rightarrow \infty$ in S. This contradicts (3.12). So $\sup \{t_{m}:m\in N_{0}\}<1$. Similarly, we can show $\inf \{t_{m}:m\in N_{0}\}>0$. Let $c_{0}$ and $c_{1}$ be selected as in (3.17). The expressions (3.14), (3.15) and (3.16) imply

$$\begin{aligned} \frac{ \vert \dot{u}_{m}(t) \vert }{g(u_{m}(t))}\leq \biggl\{ 1+ \frac{h(r+\mu ^{\ast})}{g(r+\mu ^{\ast})} \biggr\} V(t),\quad t\in (0,1), \end{aligned}$$

where

$$\begin{aligned} V(t)= { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{s_{1}}{2})}} \bigl(\max \{t,c_{1} \}-\min \{t,c_{0}\} \bigr). \end{aligned}$$

It is easy to check that $V\in L^{1}[0,1]$. Define $I:[0,\infty )\rightarrow [0,\infty )$

$$\begin{aligned} I(z)= { \int _{0}^{z}}\frac{dx}{g(x)}. \end{aligned}$$

Then I is an increasing map from $[0,\infty )$ onto $[0,\infty )$ and $I(\infty )=\infty$ because $g(u)>0$ is non-increasing on $(0,\infty )$. Also, I is continuous on $[0,C]$ for any $C>0$. So $\{I(u_{m})\}_{m\in N_{0}}$ is bounded; therefore,

$$\begin{aligned} \bigl\{ I(u_{m})\bigr\} _{m\in N_{0}}\quad \text{is a bounded and equicontinuous family on } [0, 1]. \end{aligned}$$

(3.18)

The equicontinuity follows from (here $t, s\in [0,1]$)

$$\begin{aligned} \bigl\vert I\bigl(u_{m}(t)\bigr)-I\bigl(u_{m}(s)\bigr) \bigr\vert = \biggl\vert { \int _{s}^{t}} \frac{\dot{u}_{m}(t)}{g(u_{m}(t))}\,dt \biggr\vert \leq \biggl\{ 1+ \frac{h(r+\mu ^{\ast})}{g(r+\mu ^{\ast})} \biggr\} \biggl\vert { \int _{s}^{t}}V(x)\,dx \biggr\vert . \end{aligned}$$

According to the fact (3.18), the uniform continuity of $I^{-1}$ on $[0,I(r+\mu ^{\ast})]$ and

$$\begin{aligned} \bigl\vert u_{m}(t)-u_{m}(s) \bigr\vert = \bigl\vert I^{-1}\bigl(I\bigl(u_{m}(t)\bigr)\bigr)-I^{-1} \bigl(I\bigl(u_{m}(s)\bigr)\bigr) \bigr\vert . \end{aligned}$$

We now prove (3.13).

By the Arzela–Ascoli Theorem [37], there exists a subsequence N of $N_{0}$ and a function $u\in C[0,1]$ such that $u_{m}$ converges uniformly on $[0,1]$ to u as $m\rightarrow \infty$ through N. Also, $u(0)=u(1)=0$, $0<\|u\|\leq r$ and $u(t)\geq kt(1-t)$ for $t\in [0,1]$. For each $t\in (0,1)$, we can follow the argument in [1] to obtain

$$\begin{aligned} \ddot{u}(t)- { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}}F\bigl(t,u(t)+ \mu (t)\bigr)=0 \quad\text{for } 0< t< 1. \end{aligned}$$

Furthermore, it is easy to see that $\|u\|< r$ (note if $\|u\|=r$, a contradiction will be yielded by the essential argument from (3.4)–(3.9)). □

In what follows, we found the existence of two nonnegative solutions to the singular second-order Dirichlet boundary value problem

$$\begin{aligned} \textstyle\begin{cases} \ddot{u}(t)+ { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}} [g(u(t))+h(u(t)) ]+\beta (t) =0,\quad 0< t< 1, \\ u(0)=0,\qquad u(1)=0,\end{cases}\displaystyle \end{aligned}$$

(3.19)

where $\beta (t)$ is described as in (1.12), nonlinear term $g(u)\in {\mathbb{C}}((0,1)\times {\mathbb{R}}\backslash \{0\},{ \mathbb{R}})$, and $h(u)\in {\mathbb{C}}((0,1)\times {\mathbb{R}},{\mathbb{R}})$, $g(u)$ may be singular at $u=0$. From Theorem 3.1, we have immediately the following existence result for (3.19).

Theorem 3.2

Suppose that ${\mathrm{(H_{3})}}$ and the following condition hold:

${\mathrm{( H_{4})}}$:

$g(u)>0$ is non-increasing, $h(u)\geq 0$ and $h(u)/g(u)$ is non-decreasing in u;

Then (3.19) has a nonnegative solution u with $u(t)>0$ for all $t\in (0,1)$ and $0<\|u-\mu \|<r$. ${\mathbf{Proof.}}$ As in the proof of Theorem 3.1, we take $F(t,u)=-g(u)-h(u)$. So ${\mathrm{(H_{1})}}$ is satisfied with $\phi _{r+\mu ^{\ast}}(t)=g(r+\mu ^{\ast})$.

Theorem 3.3

Suppose that ${\mathrm{(H_{3})}}$ and ${\mathrm{(H_{4})}}$ and the following condition hold:

${\mathrm{(H_{5})}}$:

choose $c\in (0,\frac{1}{2})$, fix it, and assume that there exists $R>r$ such that

$$\begin{aligned} { \frac{R}{g(R+\mu ^{\ast}) \{1+ {\frac{h(\sigma R+\mu _{\ast})}{g(\sigma R+\mu _{\ast})}} \}}} \leq { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{s_{2}}{2})}} { \int _{c}^{1-c}}G(\zeta ,\tau )\,d\tau , \end{aligned}$$

here $\sigma =c(1-c)$ and $0\leq \zeta \leq 1$ is satisfying

$$\begin{aligned} { \int _{c}^{1-c}}G(\zeta ,\tau )\,d\tau =\sup _{0 \leq t\leq 1} { \int _{c}^{1-c}}G(t,\tau )\,d\tau . \end{aligned}$$

Then (3.19) has at least a nonnegative solution ũ with $\tilde{u}(t)>0$ for $t\in (0,1)$ and $r<\|\tilde{u}-\mu \|\leq R$.

Proof

As a similar argument in the proof of Theorem 3.1, it is only needed to prove that

$$\begin{aligned} \textstyle\begin{cases} \ddot{u}(t)+ { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}} [g(u(t)+\mu (t))+h(u(t)+\mu (t)) ]=0,\quad 0< t< 1, \\ u(0)=0, \qquad u(1)=0,\end{cases}\displaystyle \end{aligned}$$

(3.20)

has a solution $\tilde{u}\in X$ with $\tilde{u}(t)+\mu (t)>0$ on $(0,1)$ and $r<\|\tilde{u}\|\leq R$.

Since ${\mathrm{(H_{3})}}$ holds, a positive constant $\varepsilon < r$ can be chosen, such that (3.1) holds. Choose $n_{1}\in \{1,2,\ldots \}$ satisfying $\frac{1}{n_{1}}<\min \{\frac{\varepsilon}{2}, \sigma R \}$ and let $N_{1}=\{n_{1},n_{1}+1,\ldots \}$. We consider the family of systems

$$\begin{aligned} \textstyle\begin{cases} \ddot{u}(t)+ { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}} [g^{m}(u(t)+\mu (t))+h(u(t)+\mu (t)) ]=0,\quad 0< t< 1, \\ u(0)=\frac{1}{m},\qquad u(1)=\frac{1}{m},\end{cases}\displaystyle \end{aligned}$$

(3.21)

where

$$\begin{aligned} g^{m}(u)=\textstyle\begin{cases} g(u) ,& u\geq \frac{1}{m}, \\ g(\frac{1}{m}) ,& u\leq \frac{1}{m}\end{cases}\displaystyle \end{aligned}$$

We know that $g^{m}(u)\leq g(u)$ for $u\in [0,\infty )$ since $g(u)$ is non-increasing.

Define a set

$$\begin{aligned} K=\bigl\{ u\in X:u(t)\geq t(1-t) \Vert u \Vert \text{ for } t\in [0,1]\bigr\} . \end{aligned}$$

Clearly K is a cone in X. Define the open sets

$$\begin{aligned} \Omega ^{1}=\bigl\{ u\in X: \Vert u \Vert < r\bigr\} , \qquad\Omega ^{2}=\bigl\{ u\in X: \Vert u \Vert < R\bigr\} \end{aligned}$$

and the operator $S:\overline{\Omega}^{2}_{K}\backslash \Omega ^{1}_{K}\rightarrow K$:

$$\begin{aligned} (Su) (t)=\frac{1}{m}+ { \int _{0}^{1}G(t,\tau ) { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})\tau +s_{1}}{2})}} \bigl[g^{m}\bigl(u(\tau )+\mu (\tau )\bigr)+h\bigl(u(\tau )+\mu (\tau ) \bigr) \bigr]\,d\tau}. \end{aligned}$$

A standard argument implies that $S:\overline{\Omega}^{2}_{K}\backslash \Omega ^{1}_{K}\rightarrow X$ is continuous and completely continuous. If $u\in K$, then $(Su)(t)\geq 0$ for all $t\in [0,1]$. We also notice that

$$\begin{aligned} &(Su)''(t)\leq 0 \quad\text{on } (0,1),\\ &(Su) (0)=(Su) (1)=\frac{1}{m}, \end{aligned}$$

so $(Su)(t)$ is concave on $[0,1]$ and $Su\in K$. Therefore, $S:\overline{\Omega}^{2}_{K}\backslash \Omega ^{1}_{K}\rightarrow K$ is well defined.

In what follows, we will use Theorem 2.4 to show that S has at least one fixed point. Firstly we will declare that: (i) $u\neq \lambda Su$ for $\lambda \in [0,1)$ and $u\in \partial _{K}\Omega ^{1}$. Suppose it is false, i.e., there exist $u\in \partial _{K}\Omega ^{1}$ and $\lambda \in [0,1)$ such that $u=\lambda Su$. We can suppose that $\lambda \neq 0$. Now since $u\in \partial _{K}\Omega ^{1}$, we have $\|u\|=r$. Since $u=\lambda Su$, we have

$$\begin{aligned} \textstyle\begin{cases} \ddot{u}(t)+\lambda { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}} [g^{m}(u(t)+\mu (t))+h(u(t)+\mu (t)) ]=0,\quad 0< t< 1, \\ u(0)=\frac{1}{m}, \qquad u(1)=\frac{1}{m}.\end{cases}\displaystyle \end{aligned}$$

We notice that

$$\begin{aligned} \ddot{u}=-\lambda { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}} \bigl[g^{m}\bigl(u(t)+\mu (t) \bigr)+h\bigl(u(t)+\mu (t)\bigr) \bigr]\leq 0,\quad 0\leq t \leq 1 \end{aligned}$$

So, we have $u(t)\geq \frac{1}{m}>0$ on $[0,1]$, and there exists $t_{0}\in (0,1)$ such that $\dot{u}(t)\geq 0$ on $(0,t_{0})$, $\dot{u}(t)\leq 0$ on $(t_{0},1)$ and $u(t_{0})=\|u\|=r$. We also observe that

$$\begin{aligned} g^{m}\bigl(u(t)+\mu (t)\bigr)+h\bigl(u(t)+\mu (t)\bigr)\leq g \bigl(u(t)+\mu (t)\bigr)+h\bigl(u(t)+\mu (t)\bigr), \quad 0< t< 1. \end{aligned}$$

Then as a similar argument in the proof of the Theorem 3.1, a contradiction can lead to ${\mathrm{(H_{3})}}$, so (i) is proved.

Then we will claim that (ii) there exists $v\in K\backslash \{0\}$ such that $u\neq Su+\lambda v$ for all $u\in \partial _{K}\Omega ^{2}$ and all $\lambda >0$. Let $v(t)\equiv 1$, then $v\in K\backslash \{0\}$. Suppose it is false, i.e. there exist $u\in \partial _{K}\Omega ^{2}$ and $\lambda >0$ such that $u=Su+\lambda v$, then $\|u\|=R$, and u is concave on $[0,1]$. According to Lemma 2.1, we have that

$$\begin{aligned} u(t)\geq t(1-t)R,\quad 0\leq t\leq 1. \end{aligned}$$

Particularly, for $t\in [c,1-c]$, we have

$$\begin{aligned} \sigma R=c(1-c)R\leq u(t)\leq R \end{aligned}$$

and

$$\begin{aligned} \frac{1}{m}< \sigma R\leq \sigma R+\mu _{\ast}\leq u(t)+\mu (t)\leq R+ \mu ^{\ast}. \end{aligned}$$

(3.22)

Therefore, we have $g^{m}(u(t)+\mu (t))= g(u(t)+\mu (t))$ for $t\in [c,1-c]$. Then using (3.22) and ${\mathrm{(H_{4})}}$, we have

$$\begin{aligned} u(\zeta ) &= (Su) (\zeta )+\lambda \\ &= \frac{1}{m}+ { \int _{0}^{1}G(\zeta , \tau ) { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})\tau +s_{1}}{2})}} \bigl[g^{m}\bigl(u(\tau )+\mu (\tau )\bigr)+h\bigl(u(\tau )+\mu (\tau )\bigr) \bigr]\,d\tau}+ \lambda \\ &> { \int _{c}^{1-c}}G(\zeta ,\tau ) { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})\tau +s_{1}}{2})}}g\bigl(u( \tau )+\mu (\tau )\bigr) \biggl\{ 1+ \frac{h(u(\tau )+\mu (\tau ))}{g(u(\tau )+\mu (\tau ))} \biggr\} \,d\tau + \lambda \\ &\ge g\bigl(R+\mu ^{\ast}\bigr) \biggl\{ 1+ \frac{h(\sigma R+\mu _{\ast})}{g(\sigma R+\mu _{\ast})} \biggr\} {\frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{s_{2}}{2})}} { \int _{c}^{1-c}}G(\zeta ,\tau )\,d\tau +\lambda . \end{aligned}$$

Therefore,

$$\begin{aligned} R>g\bigl(R+\mu ^{\ast}\bigr) \biggl\{ 1+ \frac{h(\sigma R+\mu _{\ast})}{g(\sigma R+\mu _{\ast})} \biggr\} { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{s_{2}}{2})}} { \int _{c}^{1-c}}G(\zeta ,\tau )\,d\tau +\lambda . \end{aligned}$$

This contradicts ${\mathrm{(H_{5})}}$, and (ii) is proved.

By Theorem 2.4, S has at least one fixed point $u_{m}\in \overline{\Omega}^{2}_{K}\backslash \Omega ^{1}_{K}$ with $r\leq \|u_{m}\|\leq R$. We claim that $\|u_{m}\|>r$, in fact, suppose $\|u_{m}\|=r$, then following the same argument will produce a contradiction. Therefore, (3.21) has a solution $u_{m}$ with $u_{m}(t)\geq \frac{1}{m}$ for $0\leq t\leq 1$. This implies that the following boundary value problem

$$\begin{aligned} \textstyle\begin{cases} \ddot{u}(t)+ { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}} [g(u(t)+\mu (t))+h(u(t)+\mu (t)) ]=0,\quad 0< t< 1, \\ u(0)=\frac{1}{m}, \qquad u(1)=\frac{1}{m},\end{cases}\displaystyle \end{aligned}$$

has a solution $u_{m}$ with

$$\begin{aligned} u_{m}(t)\geq \frac{1}{m},\quad 0\leq t\leq 1;\qquad r< \Vert u_{m} \Vert \leq R \end{aligned}$$

and

$$\begin{aligned} u_{m}(t)\geq t(1-t)r,\quad 0\leq t\leq 1. \end{aligned}$$

Next as a similar way in the proof of Theorem 3.1, we can also show that

$$\begin{aligned} \{u_{m}\}_{m\in N_{0}} \quad\text{is a bounded and equicontinuous family on } [0, 1]. \end{aligned}$$

Using the Arzela–Ascoli Theorem again, there is a subsequence N of $N_{0}$ and a function $u\in C[0,1]$ such that $u_{m}$ converges uniformly on $[0,1]$ to u as $m\rightarrow \infty$ through N. Also $u(0)=u(1)=0$, $r<\|u\|\leq R$ and $u(t)\geq t(1-t)r$ for $0\leq t\leq 1$. Therefore, using the similar argument as in the proof of [1], we can show that for each $t\in (0,1)$

$$\begin{aligned} \ddot{u}(t)+ { \frac{(s_{2}-s_{1})^{2}}{4\cosh ^{2}(\frac{(s_{2}-s_{1})t+s_{1}}{2})}} \bigl[g\bigl(u(t)+\mu (t)\bigr)+h\bigl(u(t)+ \mu (t)\bigr) \bigr]=0. \end{aligned}$$

That means u is a positive solution of (3.20) with $r< \|u\|\leq R$. □

According to the Theorem 3.2 and 3.3, it is easy to obtain the following multiplicity results for (3.19).

Theorem 3.4

Suppose that ${\mathrm{(H_{3})}}$–${\mathrm{(H_{5})}}$ are satisfied. Then (3.19) has at least two nonnegative solutions $u(t)>0$, $\tilde{u}(t)>0$ for all $t\in (0,1)$ and $\|u-\mu \|< r<\|\tilde{u}-\mu \|\leq R$.

Theorem 3.5

Assume that $a>0$, $b\geq 0$,

• (i) if $b<1$, then for each $\nu >0$, the boundary value problem (1.14) has at least one positive solution.

• (ii) if $b\geq 1$, then for each ν with $0<\nu <\nu _{1}$, the boundary value problem (1.14) has at least one positive solution, where $\nu _{1}$ is some positive constant.

• (iii) if $b>1$, then for each $0<\nu <\nu _{1}$, the boundary value problem (1.14) has at least two positive solution.

Proof

Theorem 3.3 is applied to system (1.14). We take $F(t,u)= {-u^{-a}}-\nu u^{b}$, then $F(t,u)\leq 0$, $\lim_{u\rightarrow 0^{+}}F(t,u)=-\infty$. Let $g(u)= {u^{-a}}$, $h(u)= {\nu u^{b}}$, then ${\mathrm{(H_{4})}}$ holds. If there exists a positive number r satisfying

$$\begin{aligned} \nu < { \frac{24\cosh ^{2}(\frac{s_{1}}{2})r^{a+1}-(s_{2}-s_{1})^{2}(a+1)}{(s_{2}-s_{1})^{2}(a+1)(r+\mu ^{\ast})^{a+b}}}, \end{aligned}$$

then the condition ${\mathrm{(H_{3})}}$ holds. Thus, boundary value problem (1.14) has at least one positive solution if

$$\begin{aligned} 0< \nu < \nu _{1}=\sup_{r>0} { \frac{24\cosh ^{2}(\frac{s_{1}}{2})r^{a+1}-(s_{2}-s_{1})^{2}(a+1)}{(s_{2}-s_{1})^{2}(a+1)(r+\mu ^{\ast})^{a+b}}}. \end{aligned}$$

Note that if $b<1$ then $\nu _{1}=\infty$ and if $b\geq 1$ then $\nu _{1}<\infty$, we have the results (i) and (ii).

If $b>1$, we take $c= {\frac{1}{5}}$ and fix it. Then condition ${\mathrm{(H_{5})}}$ becomes

$$\begin{aligned} \nu \geq \frac{4\cosh ^{2}(\frac{s_{2}}{2})R(R+\mu ^{\ast})^{a}-(s_{2}-s_{1})^{2}L}{(s_{2}-s_{1})^{2}L(\sigma R+\mu _{\ast})^{a+b}}, \end{aligned}$$

(3.23)

where

$$\begin{aligned} L=\max_{0\leq t\leq 1} { \int _{\frac{1}{5}}^{ \frac{4}{5}}}G(t,s)\,ds. \end{aligned}$$

Since $b>1$, the right-hand side of (3.23) tends to 0 as $R\rightarrow +\infty$. Then, for any $0<\nu <\nu _{1}$, it can find R large enough such that (3.23) is satisfied. Therefore, boundary value problem (1.14) has another solution. We have the result (iii). □

4 Conclusions

In the article, using the Leray–Schauder alternative principle and a well-known fixed point theorem in cones, we establish the existence results of multiple positive solutions for a second-order Dirichlet problem modeling the ocean flow of the Antarctic Circumpolar Current (ACC). We pay special attention to the nonlinear term $F(t,u)$, which represents the negative oceanic vorticity function and is singular at the origin; in other words, the function has an attractive singularity. Some recent results of the ocean flow for the Antarctic Circumpolar Current are generalized and enriched.