Abstract
Let  be a uniformly convex Banach space, and let
be a uniformly convex Banach space, and let  be a pair of mean nonexpansive map**s. In this paper, it is proved that the sequence of Ishikawa iterations associated with
be a pair of mean nonexpansive map**s. In this paper, it is proved that the sequence of Ishikawa iterations associated with  and
and  converges to the common fixed point of
converges to the common fixed point of  and
and  .
.
Similar content being viewed by others
1. Introduction and Preliminaries
Let  be a Banach space and let
be a Banach space and let  ,
,  be map**s from
be map**s from  to
to  . The pair of mean nonexpansive map**s was introduced by Bose in [1]:
. The pair of mean nonexpansive map**s was introduced by Bose in [1]:

for all  ,
,  ,
,  .
.
The Ishikawa iteration sequence  of
of  and
and  was defined by
was defined by

where  ,
,  . The recursion formulas (1.2) were first introduced in 1994 by Rashwan and Saddeek [2] in the framework of Hilbert spaces.
. The recursion formulas (1.2) were first introduced in 1994 by Rashwan and Saddeek [2] in the framework of Hilbert spaces.
In recent years, several authors (see [2–6]) have studied the convergence of iterations to a common fixed point for a pair of map**s. Rashwan has studied the convergence of Mann iterations to a common fixed point (see [5]) and proved that the Ishikawa iterations converge to a unique common fixed point in Hilbert spaces (see [2]). Recently, Ćirić has proved that if the sequence of Ishikawa iterations sequence  associated with
associated with  and
and  converges to
converges to  , then
, then  is the common fixed point of
is the common fixed point of  and
and  (see [7]). In [4, 6], the authors studied the same problem. In [1], Bose defined the pair of mean nonexpansive map**s, and proved the existence of the fixed point in Banach spaces. In particular, he proved the following theorem.
(see [7]). In [4, 6], the authors studied the same problem. In [1], Bose defined the pair of mean nonexpansive map**s, and proved the existence of the fixed point in Banach spaces. In particular, he proved the following theorem.
Theorem 1.1 ([1]).
Let  be a uniformly convex Banach space and
be a uniformly convex Banach space and  a nonempty closed convex subset of
a nonempty closed convex subset of  ,
,  and
and  are a pair of mean nonexpansive map**s, and
are a pair of mean nonexpansive map**s, and  . Then,
. Then,
-
(i)
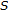 and
and  have a common fixed point
have a common fixed point  ;
; -
(ii)
further, if
 , then
, then-
(a)
 is the unique common fixed point and unique as a fixed point of each
is the unique common fixed point and unique as a fixed point of each  and
and  ,
, -
(b)
the sequence
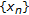 defined by
defined by 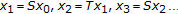 , for any
, for any 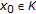 , converges strongly to
, converges strongly to  .
.
-
(a)
It is our purpose in this paper to consider an iterative scheme, which converges to a common fixed point of the pair of mean nonexpansive map**s. Theorem 2.1 extends and improves the corresponding results in [1].
2. Main Results
Now we prove the following theorem which is the main result of this paper.
Theorem 2.1.
Let  be a uniformly convex Banach space,
be a uniformly convex Banach space,  and
and  are a pair of mean nonexpansive with a nonempty common fixed points set; if
are a pair of mean nonexpansive with a nonempty common fixed points set; if  , then the Ishikawa sequence
, then the Ishikawa sequence  converges to the common fixed point of
converges to the common fixed point of  and
and  .
.
Proof.
First, we show that the sequence  is bounded. For a common fixed point
is bounded. For a common fixed point  of
of  and
and  , we have
, we have

Let  , by
, by  , it is easy to see that
, it is easy to see that  , thus
, thus  and
and  .
.
Similarly, we have  ,
,

So

Hence,  is bounded.
is bounded.
Second, we show that

We recall that Banach space  is called uniformly convex if
is called uniformly convex if  for every
for every  , where the modulus
, where the modulus  of convexity of
of convexity of  is defined by
is defined by

for every  with
with  . It is easy to see that Banach space
. It is easy to see that Banach space  is uniformly convex if and only if for any
is uniformly convex if and only if for any  implies
implies  .
.
Assume that  , then there exist a subsequence
, then there exist a subsequence  of
of  and a real number
and a real number  , such that
, such that

On the other hand, for a common fixed point  of
of  and
and  , we have
, we have

Thus,

Because

we know  is bounded, then there exists
is bounded, then there exists  , such that
, such that  . Thus,
. Thus,  .
.
Furthermore, we have

From

and the fact that  is uniformly convex Banach space, there exists
is uniformly convex Banach space, there exists  , such that
, such that

Thus,

Using (2.3), we obtain that

So

Let  , then we have
, then we have  . It is a contradiction. Hence,
. It is a contradiction. Hence,  .
.
Third, we show that

Since

we have

Let  , then
, then

So

Using (2.4), we get that

Forth, we show that if the Ishikawa sequence  converges to some point
converges to some point  , then
, then  is the common fixed point of
is the common fixed point of  and
and  . By
. By

we have  . Since
. Since  is a convergent sequence, we get
is a convergent sequence, we get  . It is easy to see that
. It is easy to see that  and
and  . On the other hand,
. On the other hand,

By (1.1), we obtain

Since

we get

So

Let  , Since
, Since  , we have
, we have

It is easy to see that

Note that  , then we get
, then we get

So  .
.
Let  , then
, then  . By (1.1), we have
. By (1.1), we have

Let  , then we get
, then we get

Since  , it follows that
, it follows that

Similarly, we can prove that  . So
. So  is the common fixed point of
is the common fixed point of  and
and  .
.
Finally, we show that  is a Cauchy sequence. For any
is a Cauchy sequence. For any  ,
,

Since  , thus we get
, thus we get  Simplify, then we have
Simplify, then we have

where  , and
, and 

 By (2.16) and (2.30), we know that
By (2.16) and (2.30), we know that

So it is easy to see that  . Thus,
. Thus,  , that is
, that is  is a Cauchy sequence. Hence, there exists
is a Cauchy sequence. Hence, there exists  , such that
, such that  . We know that
. We know that  and
and  is the common fixed point of
is the common fixed point of  and
and  . This completes the proof of the theorem.
. This completes the proof of the theorem.
References
Bose SC: Common fixed points of map**s in a uniformly convex Banach space. Journal of the London Mathematical Society 1978, 18(1):151-156. 10.1112/jlms/s2-18.1.151
Rashwan RA, Saddeek AM: On the Ishikawa iteration process in Hilbert spaces. Collectanea Mathematica 1994, 45(1):45-52.
Berinde V: On the convergence of the Ishikawa iteration in the class of quasi contractive operators. Acta Mathematica Universitatis Comenianae 2004, 73(1):119-126.
Maingé P-E: Approximation methods for common fixed points of nonexpansive map**s in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007, 325(1):469-479. 10.1016/j.jmaa.2005.12.066
Rashwan RA: On the convergence of Mann iterates to a common fixed point for a pair of map**s. Demonstratio Mathematica 1990, 23(3):709-712.
Song Y, Chen R: Iterative approximation to common fixed points of nonexpansive map** sequences in reflexive Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2007, 66(3):591-603. 10.1016/j.na.2005.12.004
Ćirić LjB, Ume JS, Khan MS: On the convergence of the Ishikawa iterates to a common fixed point of two map**s. Archivum Mathematicum 2003, 39(2):123-127.
Acknowledgment
The work was partially supported by the Emphases Natural Science Foundation of Guangdong Institution of Higher Learning, College and University (no. 05Z026).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Gu, Z., Li, Y. Approximation Methods for Common Fixed Points of Mean Nonexpansive Map** in Banach Spaces. Fixed Point Theory Appl 2008, 471532 (2008). https://doi.org/10.1155/2008/471532
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/471532




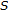 and
and  have a common fixed point
have a common fixed point  ;
; , then
, then is the unique common fixed point and unique as a fixed point of each
is the unique common fixed point and unique as a fixed point of each  and
and  ,
,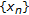 defined by
defined by 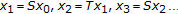 , for any
, for any 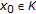 , converges strongly to
, converges strongly to  .
.