Abstract
Non-adiabatic holonomic quantum computation in decoherence-free subspaces protects quantum information from control imprecisions and decoherence. For the non-collective decoherence that each qubit has its own bath, we show the implementations of two non-commutable holonomic single-qubit gates and one holonomic nontrivial two-qubit gate that compose a universal set of non-adiabatic holonomic quantum gates in decoherence-free-subspaces of the decoupling group, with an encoding rate of  . The proposed scheme is robust against control imprecisions and the non-collective decoherence and its non-adiabatic property ensures less operation time. We demonstrate that our proposed scheme can be realized by utilizing only two-qubit interactions rather than many-qubit interactions. Our results reduce the complexity of practical implementation of holonomic quantum computation in experiments. We also discuss the physical implementation of our scheme in coupled microcavities.
. The proposed scheme is robust against control imprecisions and the non-collective decoherence and its non-adiabatic property ensures less operation time. We demonstrate that our proposed scheme can be realized by utilizing only two-qubit interactions rather than many-qubit interactions. Our results reduce the complexity of practical implementation of holonomic quantum computation in experiments. We also discuss the physical implementation of our scheme in coupled microcavities.
Similar content being viewed by others
Introduction
Holonomic quantum computation (HQC), first proposed by Zanardi and Rasetti1, is a general procedure for implementing quantum gates using non-Abelian geometric phases. In HQC, unitary operations can be implemented by varying the system Hamiltonian with degenerate energy levels to make the system evolve along a closed path in the parameter space. The unitary operations are determined only by the shape of the closed path, not on the details of the evolution. The property of HQC against control imprecisions leads to robust quantum operations. Thus HQC has become one promising quantum computation paradigm and attracted more and more interests recently2,3,4,5,6,7,8,9,10,11,12,13,14. The initial HQC is based on adiabatic evolution requiring long evolution time for the desired parametric control. To deal with this drawback, non-adiabatic HQC based on non-adiabatic non-Abelian geometric phases15 has been proposed in ref. 9 and experimentally demonstrated in12,13.
Apart from errors in the control process, decoherence often caused by unavoidable interaction with environment is another main practical obstacle in quantum information processing (QIP). Various methods have been presented to protect quantum information against decoherence, such as symmetry-aided passive decoherence-free subspaces (DFSs)16 and noiseless subsystems (NSs)17 approaches, as well as active dynamical decoupling (DD)18 techniques. The basic idea of DFSs and NSs is to utilize the natural symmetry of the system-environment interaction. Information stored in subspace spanned by the quantum states or subsystems are unaffected by the interaction with the environment. DFSs and NSs have been explored extensively in various physical systems19,20,21,22,23,24,25. DD18 tackles decoherence by suppressing the system-environment interaction through stroboscopic pulsing of the system and it is thus called active approach against decoherence. As shown in the literatures26,27,28,29,30,31, DD not only can be used to preserve arbitrary state in quantum memories, it is also compatible with gate operations used for QIP in principle, essentially by designing DD operations that commute with the gate operations. Experimental demonstrations of DD protecting quantum gates have been recently achieved in different physical systems32,33. Therefore, if the system-environment interaction has naturally available symmetries, one can use DFSs/NSs to encode and store quantum information. However, often times in practical applications such symmetries are imperfect and hence DFSs/NSs itself is not enough for protecting quantum information. In this case the combination of the active DD and the passive DFSs/NSs offers effective method to mitigate the negative effect of decoherence26,31,34,35.
To protect quantum information from both control imprecisions and the detrimental effects of the environment, the schemes hybridizing HQC with DFSs based on adiabatic evolution have been proposed5,6,7. In order to avoid the long run time required by adiabatic evolution, refs. 10,11 have shown that non-adiabatic HQC can be realized in DFSs that are insensitive to the collective dephasing errors. For the general errors that each qubit has its own bath, the implementation of non-adiabatic holonomic gates can be protected from decoherence by resorting to the DD approach. According to the DD, undesirable couplings between system and environment can be effectively averaged out by utilizing repetition of fast external control operations. Due to the requirement of fast pulses, DD provides relatively less resource-demand protection for quantum information. However, the non-adiabatic HQC together with the integration of DD and DFSs/NSs has not been well explored. Very recently, Xu and Long36 proposed a non-adiabatic HQC scheme based on two-qubit interactions and the scheme is robust against non-collective decoherence, by encoding three physical qubits to one logical qubit. Consider the scalability of the proposed quantum gates to many logical qubits, the scheme proposed in36 requires a lot of resource. Thus more easily achievable scheme with a better encoding rate and against control imprecisions as well as non-collective decoherence is of great significance from the experimental perspective. In this work we address the issue by presenting a non-adiabatic HQC scheme against non-collective decoherence. We consider a linear system-bath interaction Hamiltonian in which each qubit has its own bath and provide a universal set of nonadiabatic holonomic quantum gates by presenting two noncommuting single-logical-qubit gates and one nontrivial two-logical-qubit gate in DFSs of a decoupling group. The encoding strategy used here is to encode N physical qubits to  logical qubits and hence our scheme largely reduces the complexity of experiments.
logical qubits and hence our scheme largely reduces the complexity of experiments.
Results
We first recall the active DD technique18,29 which is to be used to suppress the system-bath interaction later. In general, the interaction Hamiltonian without DD is of the form,  , where each
, where each  and
and  are pure-system operator and pure-bath operator, respectively. To suppress error, consider a group
are pure-system operator and pure-bath operator, respectively. To suppress error, consider a group  ,
,  , of unitary transformations
, of unitary transformations  acting purely on the system with
acting purely on the system with  1being the identity matrix and
1being the identity matrix and  order
order  denoting the number of group elements. Assuming that each such pulse
denoting the number of group elements. Assuming that each such pulse  is effectively instantaneous and their temporal separation is
is effectively instantaneous and their temporal separation is  , a full cycle time is
, a full cycle time is  and the natural propagator is
and the natural propagator is  . Then the evolution of the whole system with DD over a single cycle time is given by
. Then the evolution of the whole system with DD over a single cycle time is given by  , where
, where  denotes the resulting effective Hamiltonian. In the ideal limit of arbitrarily fast control
denotes the resulting effective Hamiltonian. In the ideal limit of arbitrarily fast control  ,
,  approaches
approaches  . Note that
. Note that  for
for  , thereby the decoupled evolution is symmetrized according to
, thereby the decoupled evolution is symmetrized according to  .
.
A decomposition of the system Hilbert space  can be induced by the decoupling group
can be induced by the decoupling group  via its group algebra
via its group algebra  and its commutant algebra
and its commutant algebra  as follows24,29:
as follows24,29:  ,
,  and
and  . Here the J-th irreducible representation (irrep), with the dimension
. Here the J-th irreducible representation (irrep), with the dimension  , appears with the multiplicity
, appears with the multiplicity  , while
, while  and
and  are, respectively, the complex-valued
are, respectively, the complex-valued  matrices and the
matrices and the  identity matrix. We encode the computational state into the left factor
identity matrix. We encode the computational state into the left factor  , the effective Hamiltonian
, the effective Hamiltonian  needs to act trivially on
needs to act trivially on  . A necessary and sufficient condition is
. A necessary and sufficient condition is 
 . In this case subsystems
. In this case subsystems  are called NSs. When
are called NSs. When  , the DFSs case arises.
, the DFSs case arises.
We consider a linear system-bath interaction Hamiltonian which is described by,

where  are Pauli matrices acting on the i-th qubit and
are Pauli matrices acting on the i-th qubit and  are arbitrary bath operators. In this noise model, each qubit has its own bath. The decoupling group for N-qubit can be selected as29:
are arbitrary bath operators. In this noise model, each qubit has its own bath. The decoupling group for N-qubit can be selected as29:  , where the pulses
, where the pulses  ,
,  and
and  . Based on
. Based on  , the resulting average system-bath interaction becomes
, the resulting average system-bath interaction becomes  , which implies that the system is decoupled from the bath up to first-order at the time instant
, which implies that the system is decoupled from the bath up to first-order at the time instant  .
.
Suppose that N is even,  is an Abelian group with order
is an Abelian group with order  , thus all the irreps of
, thus all the irreps of  are 1-dimensional (i.e.,
are 1-dimensional (i.e.,  and the number of irreps is the order of the group. The group algebra
and the number of irreps is the order of the group. The group algebra  can be written as
can be written as  , where
, where  . Therefore each of the four equivalent subspaces (DFSs) is able to encode
. Therefore each of the four equivalent subspaces (DFSs) is able to encode  logical qubits to make universal quantum computation. For instance, the
logical qubits to make universal quantum computation. For instance, the  -invariant subspace
-invariant subspace  , representing a set of eigenvalues of decoupling group elements, is spanned by the N-qubit quantum states
, representing a set of eigenvalues of decoupling group elements, is spanned by the N-qubit quantum states  , with r containing an even number of
, with r containing an even number of  of length N.
of length N.
For the system-bath interaction form (1), the decoupling group  used to decouple the system from the bath up to first-order at the time instant
used to decouple the system from the bath up to first-order at the time instant  , has four equivalent
, has four equivalent  -dimensional DFSs with N being even. Each of the four equivalent DFSs is able to encode
-dimensional DFSs with N being even. Each of the four equivalent DFSs is able to encode  logical qubits to make universal quantum computation29 (i.e., there are
logical qubits to make universal quantum computation29 (i.e., there are  logical qubits in each DFS that will be unaffected by the system-bath interaction). In the following, we utilize one of the four equivalent
logical qubits in each DFS that will be unaffected by the system-bath interaction). In the following, we utilize one of the four equivalent  -invariant DFSs (i.e.,
-invariant DFSs (i.e.,  to encode our qubits. The
to encode our qubits. The  logical qubits are encoded in such subspace and the logical states are
logical qubits are encoded in such subspace and the logical states are

where  and
and  are the logical states of
are the logical states of  logical qubits and the subscript L is used to denote that the states (or the operators) are logical states (or operators).
logical qubits and the subscript L is used to denote that the states (or the operators) are logical states (or operators).  and
and  are the quantum states of
are the quantum states of  physical qubits from the 2-th to the
physical qubits from the 2-th to the  -th physical qubits, with
-th physical qubits, with  and
and  , respectively, containing an even number and an odd number of
, respectively, containing an even number and an odd number of  of length
of length  . For instance, the logical states for N = 4 read
. For instance, the logical states for N = 4 read

To implement two noncommuting holonomic single-logical-qubit gates and one nontrivial holonomic two-logical-qubit gate, one needs a set of operators to achieve the appropriate transitions so that the evolution stays within the DFS. To this end, we need to seek for the operators that commute with the decoupling group  . Here we consider the operators
. Here we consider the operators 
 which commute with the decoupling group
which commute with the decoupling group  . One can use a combination of the above operators to construct desired Hamiltonians and as a result the DFS will not be destroyed.
. One can use a combination of the above operators to construct desired Hamiltonians and as a result the DFS will not be destroyed.
One qubit gates
Explicitly, the forms of the Hamiltonians which generate a holonomic single-qubit gate can be taken as follows

where  and
and  are the controllable coupling parameters, θ is an arbitrary parameter and
are the controllable coupling parameters, θ is an arbitrary parameter and  . The final time evolution operator which is composed by two-step evolutions reads
. The final time evolution operator which is composed by two-step evolutions reads  , where
, where  is an intermediate time parameter and
is an intermediate time parameter and  is the evolution period. Adjust the parameters such that
is the evolution period. Adjust the parameters such that  , we show that the evolution leads to a single-logical-qubit gate. Take
, we show that the evolution leads to a single-logical-qubit gate. Take  and
and  as an example, we have the evolution operator act on the logical states in the DFS (3),
as an example, we have the evolution operator act on the logical states in the DFS (3),

It is clear that the resulting unitary operator can be written in the subspace spanned by (3) by ignoring global phase as follows  . where
. where  is the Pauli Y operator acting on the 1-th logical qubit and
is the Pauli Y operator acting on the 1-th logical qubit and  is the identity matrix acting on the 2-th logical qubit. It is straightforward to obtain the evolution operator in the subspace spanned by
is the identity matrix acting on the 2-th logical qubit. It is straightforward to obtain the evolution operator in the subspace spanned by  logical states (2) up to a global phase as
logical states (2) up to a global phase as

where N and j are arbitrary,  is the Pauli Y operator acting on the j-th logical qubit. This operator is nothing but one j-th single-logical-qubit gate
is the Pauli Y operator acting on the j-th logical qubit. This operator is nothing but one j-th single-logical-qubit gate  . It is shown that the unitary operator
. It is shown that the unitary operator  is purely holonomic according to the conditions of non-adiabatic HQC (see Methods).
is purely holonomic according to the conditions of non-adiabatic HQC (see Methods).
We next explore the realization of another holonomic j-th single-logical-qubit gate  . The desired Hamiltonians read
. The desired Hamiltonians read

where  and
and  are the controllable coupling parameters. With the two Hamiltonians and the
are the controllable coupling parameters. With the two Hamiltonians and the  and
and  in Eq. (4), the evolution operator which is composed by four-step evolution is given by
in Eq. (4), the evolution operator which is composed by four-step evolution is given by  . In the above equation,
. In the above equation,  ,
,  ,
,  and
and  are respectively intermediate time parameters and the evolution period. By choosing the following conditions
are respectively intermediate time parameters and the evolution period. By choosing the following conditions  ,
,  ,
,  and the action of the unitary evolution operator
and the action of the unitary evolution operator  is obtained for
is obtained for  and
and  ,
,

Up to a global phase, the resulting unitary operator is of the form,  , where
, where  is the logical Pauli Z operator acting on the 1-th logical qubit and
is the logical Pauli Z operator acting on the 1-th logical qubit and  is the identity matrix acting on the 2-th logical qubit. For arbitrary N and j, it is not difficult to find the evolution operator in the subspace spanned by
is the identity matrix acting on the 2-th logical qubit. For arbitrary N and j, it is not difficult to find the evolution operator in the subspace spanned by  logical states (2) by neglecting global phase,
logical states (2) by neglecting global phase,

where  is the logical Pauli Z operator acting on the j-th logical qubit. Therefore we get another j-th single-logical-qubit gate
is the logical Pauli Z operator acting on the j-th logical qubit. Therefore we get another j-th single-logical-qubit gate  , which does not commutate with
, which does not commutate with  in (6). Similar to the illustration of the geometric property of
in (6). Similar to the illustration of the geometric property of  , one can verify that the unitary operator
, one can verify that the unitary operator  also possesses holonomic property (see Methods).
also possesses holonomic property (see Methods).
As well known is that any single-logical-qubit rotation can be realized by arbitrary rotations around two orthogonal axes. Thus the above two noncommutative single-logical-qubit gates  and
and  , can realize any single-logical-qubit rotation.
, can realize any single-logical-qubit rotation.
Two qubit gate
To achieve a universal set of quantum gates, we now demonstrate how to realize an entangling gate between the k-th logical qubit and the l-th logical qubit  in the DFS spanned by (2) using the generalized off-diagonal geometric proposal37. The required Hamiltonians are
in the DFS spanned by (2) using the generalized off-diagonal geometric proposal37. The required Hamiltonians are

where  is an arbitrary parameter and
is an arbitrary parameter and  and
and  are the controllable coupling parameters. The final time evolution operator resulted from the two-step evolution is
are the controllable coupling parameters. The final time evolution operator resulted from the two-step evolution is  , where
, where  and
and  are respectively an intermediate time parameter and the evolution period. Control the parameters to make sure that
are respectively an intermediate time parameter and the evolution period. Control the parameters to make sure that  , we have
, we have  written in the DFS formed by (3) for
written in the DFS formed by (3) for  ,
,  and
and  ,
,

The unitary operator is of an equivalent form  (up to global phase). Furthermore, take
(up to global phase). Furthermore, take  ,
,  and
and  , the action of
, the action of  on the logical states in the logic DFS (2) can be found as
on the logical states in the logic DFS (2) can be found as

where  . The resulting unitary operator can be written in the subspace spanned by (2) as follows by ignoring global phase,
. The resulting unitary operator can be written in the subspace spanned by (2) as follows by ignoring global phase,  . Meanwhile, for
. Meanwhile, for  ,
,  and
and  , we get
, we get

where  . In this case, the unitary operator is
. In this case, the unitary operator is  up to a global phase. It is easy to generalize the results to any
up to a global phase. It is easy to generalize the results to any  and the evolution operator reads
and the evolution operator reads

in the subspace spanned by  logical states (2). One can find that
logical states (2). One can find that  is a nontrivial entangling logical gate when
is a nontrivial entangling logical gate when  and
and  are nonzero. The geometric feature of
are nonzero. The geometric feature of  can be demonstrated by resorting to the eigenstates of
can be demonstrated by resorting to the eigenstates of  and
and  as we did for
as we did for  and
and  respectively (see Methods). As a result, we have achieved a universal set of non-adiabatic holonomic quantum gates in DFSs of the decoupling group
respectively (see Methods). As a result, we have achieved a universal set of non-adiabatic holonomic quantum gates in DFSs of the decoupling group  with two non-commutative single-logical-qubit gates and one non-trivial holonomic two-qubit gate.
with two non-commutative single-logical-qubit gates and one non-trivial holonomic two-qubit gate.
Discussions
We next discuss the physical realization of our scheme in physical systems. The above-mentioned two-body qubit-qubit interactions required for the implementation of the quantum logic gates may be achieved in coupled microcavity system and that is an array of cavities coupled via exchange of virtual photons with one Λ-type three-level atom in each cavity38. In the literature, an anisotropic Heisenberg spin-1/2 lattice in an external magnetic field was proposed by individually adjusting the external lasers illuminated on the atoms. The effective Hamiltonian is of the form

where the parameters  ,
,  can individually be tuned via external lasers through controlling the laser frequencies, Rabi frequencies and the cavity-cavity couplings38. Based on the results, different kinds of two-body qubit-qubit interactions can be generated by suitably selecting the parameters
can individually be tuned via external lasers through controlling the laser frequencies, Rabi frequencies and the cavity-cavity couplings38. Based on the results, different kinds of two-body qubit-qubit interactions can be generated by suitably selecting the parameters  ,
,  , so our proposed logic gates may be realized in the coupled microcavity system. According to the effective qubit-qubit interaction, nearest neighbor couplings of qubits can be realized. Our desired
, so our proposed logic gates may be realized in the coupled microcavity system. According to the effective qubit-qubit interaction, nearest neighbor couplings of qubits can be realized. Our desired  and
and  are based on two-qubit interactions including the cases that the two qubits are next to each other or not. The two-qubit interactions may be achievable in the coupled microcavities by controlling the couplings of different microcavities based on Hamiltonian (15). We take
are based on two-qubit interactions including the cases that the two qubits are next to each other or not. The two-qubit interactions may be achievable in the coupled microcavities by controlling the couplings of different microcavities based on Hamiltonian (15). We take  as an example to explain the physical realization of the interaction. Number the atoms in each microcavity as 1 to N. Let
as an example to explain the physical realization of the interaction. Number the atoms in each microcavity as 1 to N. Let  -th and N-th microcavities interact with each other while the others do not. Adjust the detunings and Rabi frequencies in the two specified microcavities such that Jx and Jy are zero38, we get
-th and N-th microcavities interact with each other while the others do not. Adjust the detunings and Rabi frequencies in the two specified microcavities such that Jx and Jy are zero38, we get  . The other target two-qubit interactions can be obtained similarly.
. The other target two-qubit interactions can be obtained similarly.
In this work, we have explored the implementation of universal sets of non-adiabatic holonomic quantum gates by considering a linear system-bath interaction Hamiltonian in which each qubit has its own bath. The holonomic quantm gates are achieved in the DFSs of the decoupling group. Our results possess four-fold merits. Firstly, the quantum operations bear non-adiabatic holonomic property and hence they are robust against control imprecisions and require less operation time. Secondly, based on combination of the active DD and the passive DFSs, the quantum operations are resisted to the decoherence caused by unavoidable interaction with environment. Thirdly, our scheme is realizable by utilizing only two-body interactions rather than many-body interactions. From the perspective of experiments, two-body interactions are easier to achieve in physical systems than many-body interactions. Lastly, our encoding strategy with an encoding rate of  makes our scheme preferable consider the scalability of quantum computation to many logical qubits. In the following we would like to compare our work with the one presented in ref. 36 in which non-adiabatic HQC was also proposed in the DFS by DD based on two-qubit interactions. Compared with ref. 36, our scheme exhibits two desirable advantages. One is about the encoding rate, it is
makes our scheme preferable consider the scalability of quantum computation to many logical qubits. In the following we would like to compare our work with the one presented in ref. 36 in which non-adiabatic HQC was also proposed in the DFS by DD based on two-qubit interactions. Compared with ref. 36, our scheme exhibits two desirable advantages. One is about the encoding rate, it is  in our scheme, while in ref. 36 it is
in our scheme, while in ref. 36 it is  . The increased encoding rate is due to the fact that we encode our logical qubits in the DFS provided by the dynamical decoupling itself and hence our encoding structure is more symmetric. The other advantage is that, in our scheme any arbitrary single-logical-qubit gate can be obtained by simple combinations of the two single-logical-qubit gates proposed, where it is not the case in ref. 36. Therefore our results reduce the complexity of practical implementation of holonomic quantum gates in the DFSs of the decoupling group. We expect our scheme can shed light on the experimentally achievable implementations of HQC in DFSs.
. The increased encoding rate is due to the fact that we encode our logical qubits in the DFS provided by the dynamical decoupling itself and hence our encoding structure is more symmetric. The other advantage is that, in our scheme any arbitrary single-logical-qubit gate can be obtained by simple combinations of the two single-logical-qubit gates proposed, where it is not the case in ref. 36. Therefore our results reduce the complexity of practical implementation of holonomic quantum gates in the DFSs of the decoupling group. We expect our scheme can shed light on the experimentally achievable implementations of HQC in DFSs.
Methods
We need to verify whether the unitary operators  are purely holonomic quantum gates. The conditions of non-adiabatic HQC has been proposed in refs 9,10. Consider an N-dimensional quantum system with Hamiltonian
are purely holonomic quantum gates. The conditions of non-adiabatic HQC has been proposed in refs 9,10. Consider an N-dimensional quantum system with Hamiltonian  . Assume there exists a time-dependent K-dimensional subspace
. Assume there exists a time-dependent K-dimensional subspace  spanned by a set of orthonormal basis vectors
spanned by a set of orthonormal basis vectors  at each time t. Here
at each time t. Here  can be obtained from the Schrödinger equation
can be obtained from the Schrödinger equation  , with
, with  and T is the time ordering operator. The unitary transformation
and T is the time ordering operator. The unitary transformation  is a holonomy matrix acting on the subspace
is a holonomy matrix acting on the subspace  if
if  satisfy the two conditions:
satisfy the two conditions:  and
and  , where τ is the evolution period. Condition (i) ensures that the states in the subspace
, where τ is the evolution period. Condition (i) ensures that the states in the subspace  complete a cyclic evolution and condition (ii) ensures that the cyclic evolution is purely geometric.
complete a cyclic evolution and condition (ii) ensures that the cyclic evolution is purely geometric.
Holonomic property of U1
Here we explore the holonimic property of  by an example with
by an example with  and
and  by considering the orthonormal basis vectors
by considering the orthonormal basis vectors 
 ,
,  . Condition (i) is satisfied since the subspace spanned by
. Condition (i) is satisfied since the subspace spanned by  coincides with
coincides with  . Condition (ii) needs
. Condition (ii) needs  . This condition can be written as
. This condition can be written as  and
and  because
because  and
and  respectively commute with their evolution operators. It is easy to see that
respectively commute with their evolution operators. It is easy to see that  and
and  . Thus, both conditions (i) and (ii) are satisfied and
. Thus, both conditions (i) and (ii) are satisfied and  is a holonomic single-logical-qubit gate. One can also illustrate the geometric property of
is a holonomic single-logical-qubit gate. One can also illustrate the geometric property of  by visualizing the evolution in logical Bloch sphere as shown in Fig. 1. The Hamiltonians
by visualizing the evolution in logical Bloch sphere as shown in Fig. 1. The Hamiltonians  and
and  drive the eigenstates of
drive the eigenstates of  from point A with the eigenvalue +1 to the opposite pole B with the eigenvalue −1 and then back to point A, which completes a loop along the geodesic line ACBDA. Therefore there is no dynamical contribution during the whole evolution and the single-logical-qubit gate
from point A with the eigenvalue +1 to the opposite pole B with the eigenvalue −1 and then back to point A, which completes a loop along the geodesic line ACBDA. Therefore there is no dynamical contribution during the whole evolution and the single-logical-qubit gate  is purely geometric.
is purely geometric.
Holonomic property of U2
We look at the example with  and
and  again for the demonstration of the holonomic property of
again for the demonstration of the holonomic property of  and consider the orthonormal basis vectors
and consider the orthonormal basis vectors  . Condition (i) is fulfilled since the subspace spanned by
. Condition (i) is fulfilled since the subspace spanned by  coincides with
coincides with  . Furthermore, one needs to verify that condition (ii) is satisfied, i.e.,
. Furthermore, one needs to verify that condition (ii) is satisfied, i.e.,  . The condition can be rewritten as
. The condition can be rewritten as  ,
,  ,
,  and
and  because
because  ,
,  ,
,  and
and  respectively commute with their evolution operators. We thus find Conditions (ii) is satisfied as well and therefore
respectively commute with their evolution operators. We thus find Conditions (ii) is satisfied as well and therefore  is a holonomic single-logical-qubit gate. Similarly, one can also illustrate the geometric property of
is a holonomic single-logical-qubit gate. Similarly, one can also illustrate the geometric property of  by Fig. 1. The Hamiltonians
by Fig. 1. The Hamiltonians  ,
,  ,
,  and
and  drive the eigenstates of
drive the eigenstates of  from point C with the eigenvalue +1 completes a cyclic evolution along the geodesic line CBDAC. Hence the single-logical-qubit gate
from point C with the eigenvalue +1 completes a cyclic evolution along the geodesic line CBDAC. Hence the single-logical-qubit gate  is purely geometric.
is purely geometric.
Holonomic property of U3
We take  ,
,  and
and  as an example to show the holonomic property of
as an example to show the holonomic property of  . By defining
. By defining  and
and  , the two logical qubit states
, the two logical qubit states  form a basis of the 4-dimensional Hilbert space
form a basis of the 4-dimensional Hilbert space  . Now we split
. Now we split  into two orthogonal subspaces
into two orthogonal subspaces  and Span
and Span  and in the representation the Hamiltonian
and in the representation the Hamiltonian  and
and  read
read  ,
,  , where the matrices A and B can be written as
, where the matrices A and B can be written as  and
and  , respectively. The corresponding evolution operators for the two steps read
, respectively. The corresponding evolution operators for the two steps read

respectively and  can be shown as
can be shown as

The underlying idea is that, at time  , the two subspaces
, the two subspaces  evolved into each other and then, at time
evolved into each other and then, at time  , they return and this leads to a loop evolution in the Hilbert space and therefore condition (i) is satisfied. We then check that condition (ii) is satisfied, i.e.,
, they return and this leads to a loop evolution in the Hilbert space and therefore condition (i) is satisfied. We then check that condition (ii) is satisfied, i.e.,  . This is equivalent to
. This is equivalent to  and
and  because
because  and
and  respectively commute with their evolution operators. Thus, both conditions (i) and (ii) are satisfied and
respectively commute with their evolution operators. Thus, both conditions (i) and (ii) are satisfied and  is a holonomic two-logical-qubit gate.
is a holonomic two-logical-qubit gate.
The set of a 2-dimensional subspaces  in the 4-dimensional Hilbert space forms a Grassman manifold
in the 4-dimensional Hilbert space forms a Grassman manifold  38. The closed path C of 2-dimensional subspaces is a loop in
38. The closed path C of 2-dimensional subspaces is a loop in  . The set of all bases forms a Stiefel manifold
. The set of all bases forms a Stiefel manifold  , which is a fiber bundle with
, which is a fiber bundle with  as base manifold and with the set of 2 × 2 unitary matrices as fibers. The two steps of evolution to achieve
as base manifold and with the set of 2 × 2 unitary matrices as fibers. The two steps of evolution to achieve  correspond to two geodesic lines in
correspond to two geodesic lines in  , that transform
, that transform  to its orthogonal complement
to its orthogonal complement  and then back to
and then back to  along the geodesic lines. The accompanying non-Abelian geometric phase represents the
along the geodesic lines. The accompanying non-Abelian geometric phase represents the  fiber on the base manifold of
fiber on the base manifold of  .
.
Performance of the quantum gates with imperfect DD sequences
The fact that our holonomic quantum gates are resistant to non-collective decoherence is based on the DD approach. As a result, the existence of DD pulse errors will affect the performance of our proposed quantum gates. Here we provide some numerical results to demonstrate the effects of DD pulse errors. The decoupling strategy utilized in our work can be described by alternatively applying computational and DD operations with  sequence as the basic DD sequence.
sequence as the basic DD sequence.
One of the main errors in DD sequences is flip-angle error caused by the inaccuracy in pulse duration and Rabi frequency. With a relative flip-angle error ε, the imperfect pulse propagator reads36

where f indicates the effect of the flip-angle error,  are Pauli matrices acting on the i-th physical qubit and
are Pauli matrices acting on the i-th physical qubit and  is the rotation angle about the α axis. The angle
is the rotation angle about the α axis. The angle  is π for ideal instantaneous pulses. The fidelity of the quantum gates can be computed numerically according to the following formula36,
is π for ideal instantaneous pulses. The fidelity of the quantum gates can be computed numerically according to the following formula36,

where  is the ideal (imperfect) propagator without (with) DD pulse errors. We take the two-logical-qubit holonomic gate as an example to show the performance of our scheme in the presence of the flip-angle error. As shown in Fig. 2, it is clear that the type of error destroys the gate fidelity severely when
is the ideal (imperfect) propagator without (with) DD pulse errors. We take the two-logical-qubit holonomic gate as an example to show the performance of our scheme in the presence of the flip-angle error. As shown in Fig. 2, it is clear that the type of error destroys the gate fidelity severely when  (see the red solid curve).
(see the red solid curve).
Another main error source in DD sequences is due to the frequency detuning error which usually leads to errors in the rotation angle and the direction of the rotation axis. With a relative detuning error δ, the imperfect rotation operator is of the form36,

where d indicates the effect of frequency detuning error and the actual rotation axis is  . According to Eq. (20), we numerically find the fidelity of the two-logical-qubit holonomic gate when the frequency detuning error is presented (see Fig. 2, blue dashed curve). Our results show that the quantum gate is more tolerant to the detuning error than the flip-angle error and the results are consistent with those given in ref. 36. Hence our scheme requires high precision in adjusting pulse duration and Rabi frequency in experiments.
. According to Eq. (20), we numerically find the fidelity of the two-logical-qubit holonomic gate when the frequency detuning error is presented (see Fig. 2, blue dashed curve). Our results show that the quantum gate is more tolerant to the detuning error than the flip-angle error and the results are consistent with those given in ref. 36. Hence our scheme requires high precision in adjusting pulse duration and Rabi frequency in experiments.
Additional Information
How to cite this article: Sun, C. et al. Non-adiabatic holonomic quantum computation in linear system-bath coupling. Sci. Rep. 6, 20292; doi: 10.1038/srep20292 (2016).
References
Zanardi, P. & Rasetti, M. Holonomic quantum computation. Phys. Lett. A 264, 94 (1999).
Jones, J. A., Vedral, V., Ekert, A. & Castagnoli, G. Geometric quantum computation using nuclear magnetic resonance. Nature 403, 869 (2000).
Duan, L. M., Cirac, J. I. & Zoller, P. Geometric Manipulation of Trapped Ions for Quantum Computation. Science 292, 1695 (2001).
Zhu, S. L. & Wang, Z. D. Implementation of Universal Quantum Gates Based on Nonadiabatic Geometric Phases. Phys. Rev. Lett. 89, 097902 (2002).
Wu, L. A., Zanardi, P. & Lidar, D. A. Holonomic Quantum Computation in Decoherence-Free Subspaces. Phys. Rev. Lett. 95, 130501 (2005).
Cen, L. X., Wang, Z. D. & Wang, S. J. Scalable quantum computation in decoherence-free subspaces with trapped ions. Phys. Rev. A 74, 032321 (2006).
Zhang, X. D., Zhang, Q. H. & Wang, Z. D. Physical implementation of holonomic quantum computation in decoherence-free subspaces with trapped ions. Phys. Rev. A 74, 034302 (2006).
Feng, X. L., Wu, C. F., Sun, H. & Oh, C. H. Geometric Entangling Gates in Decoherence-Free Subspaces with Minimal Requirements. Phys. Rev. Lett. 103, 200501 (2009).
Sjöqvist, E., Tong, D. M., Hessmo, B., Johansson, M. & Singh, K. Non-adiabatic holonomic quantum computation. New J. of Phys. 14, 103035 (2012).
Xu, G. F., Zhang, J., Tong, D. M., Sjöqvist, E. & Kwek, L. C. Nonadiabatic Holonomic Quantum Computation in Decoherence-Free Subspaces. Phys. Rev. Lett. 109, 170501 (2012).
Xu, G. F. & Long, G. L. Universal Nonadiabatic Geometric Gates in Two-Qubit Decoherence-Free Subspaces. Sci. Rep. 4, 6814 (2014).
Abdumalikov, A. A. et al. Experimental realization of non-Abelian non-adiabatic geometric gates. Nature 496, 482 (2013).
Feng, G., Xu, G. & Long, G. Experimental Realization of Nonadiabatic Holonomic Quantum Computation. Phys. Rev. Lett. 110, 190501 (2013).
Zhang, J., Kwek, L. C., Sjöqvist, E., Tong, D. M. & Zanardi, P. Quantum computation in noiseless subsystems with fast non-Abelian holonomies. Phys. Rev A 89, 042302 (2014).
Anandan, J. Non-adiabatic non-abelian geometric phase. Phys. Lett. A 133, 171 (1988).
Lidar, D. A., Chuang, I. L. & Whaley, K. B. Decoherence-Free Subspaces for Quantum Computation. Phys. Rev. Lett. 81, 2594 (1998).
Knill, E., Laflamme, R. & Viola, L. Theory of Quantum Error Correction for General Noise. Phys. Rev. Lett. 84, 2525 (2000).
Viola, L., Knill, E. & Lloyd, S. Dynamical Decoupling of Open Quantum Systems. Phys. Rev. Lett. 82, 2417 (1999).
Kwiat, P. G., Berglund, A. J., Altepeter, J. B. & White, A. G. Experimental Verification of Decoherence-Free Subspaces. Science 290, 498 (2000).
Kielpinski, D. et al. A Decoherence-Free Quantum Memory Using Trapped Ions. Science 291, 1013 (2001).
Ollerenshaw, J. E., Lidar, D. A. & Kay, L. E. Magnetic Resonance Realization of Decoherence-Free Quantum Computation. Phys. Rev. Lett. 91, 217904 (2003).
Mohseni, M., Lundeen, J. S., Resch, K. J. & Steinberg, A. M. Experimental Application of Decoherence-Free Subspaces in an Optical Quantum-Computing Algorithm. Phys. Rev. Lett. 91, 187903 (2003).
Bourennane, M. et al. Decoherence-Free Quantum Information Processing with Four-Photon Entangled States. Phys. Rev. Lett. 92, 107901 (2004).
Zanardi, P. Stabilizing quantum information. Phys. Rev. A 63, 012301 (2000).
Zanardi, P. & Lloyd S. Topological Protection and Quantum Noiseless Subsystems. Phys. Rev. Lett. 90, 067902 (2003).
Viola, L. & Knill, E. Random Decoupling Schemes for Quantum Dynamical Control and Error Suppression. Phys. Rev. Lett. 94, 060502 (2005).
Khodjasteh, K. & Lidar, D. A. Fault-Tolerant Quantum Dynamical Decoupling. Phys. Rev. Lett. 95, 180501 (2005).
Yang, W. & Liu, R. B. Universality of Uhrig Dynamical Decoupling for Suppressing Qubit Pure Dephasing and Relaxation. Phys. Rev. Lett. 101, 180403 (2008).
Viola, L., Lloyd, S. & Knill, E. Universal Control of Decoupled Quantum Systems. Phys. Rev. Lett. 83, 4888 (1999).
Lidar, D. A. Towards Fault Tolerant Adiabatic Quantum Computation. Phys. Rev. Lett. 100, 160506 (2008).
West, J. R., Lidar, D. A., Fong, B. H. & Gyure M. F. High Fidelity Quantum Gates via Dynamical Decoupling. Phys. Rev. Lett. 105, 230503 (2010).
Barthel, C., Medford, J., Marcus, C. M., Hanson, M. P. & Gossard, A. C. Interlaced Dynamical Decoupling and Coherent Operation of a Singlet-Triplet Qubit. Phys. Rev. Lett. 105, 266808 (2010).
Van der Sar, T. et al. Decoherence-protected quantum gates for a hybrid solid-state spin register. Nature 484, 82 (2012).
Byrd, M. S. & Lidar, D. A. Comprehensive Encoding and Decoupling Solution to Problems of Decoherence and Design in Solid-State Quantum Computing. Phys. Rev. Lett. 89, 047901 (2002).
Wu, L. A. & Lidar, D. A. Creating Decoherence-Free Subspaces Using Strong and Fast Pulses. Phys. Rev. Lett. 88, 207902 (2002).
Xu, G. F. & Long, G. L. Protecting geometric gates by dynamical decoupling. Phys. Rev. A 90, 022323 (2014).
Mousolou, V. A., Canali, C. M. & Sjöqvist, E. Universal non-adiabatic holonomic gates in quantum dots and single-molecule magnets. New J. Phys. 16, 013029 (2014).
Hartmann, M. J., Brandão, F. G. S. L. & Plenio, M. B. Effective Spin Systems in Coupled Microcavities. Phys. Rev. Lett. 99, 160501 (2007).
Acknowledgements
This work was supported by the NSF of China (Grant Nos. 11205028, 11175043, 11405026 and 11405008), the Plan for Scientific and Technological Development of Jilin Province (Nos. 20130522145JH and 20150520083JH) and the Fundamental Research Funds for the Central Universities (Grant Nos. 14QNJJ008 and 2412015KJ009). C.F.S. was also supported in part by the Government of China through CSC. X.L.F. is supported by the NSF of Shanghai (Grant No. 15ZR1430600). J.L.C. is supported by National Basic Research Program (973 Program) of China (Grant No. 2012CB921900) and the NSF of China (Grant Nos. 11175089 and 11475089).
Author information
Authors and Affiliations
Contributions
C.S. initiated the idea. All authors developed the scheme and wrote the main manuscript text.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Sun, C., Wang, G., Wu, C. et al. Non-adiabatic holonomic quantum computation in linear system-bath coupling. Sci Rep 6, 20292 (2016). https://doi.org/10.1038/srep20292
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep20292
- Springer Nature Limited
This article is cited by
-
Nonadiabatic holonomic quantum computation and its optimal control
Science China Information Sciences (2023)
-
Nonadiabatic geometric quantum computation protected by dynamical decoupling via the XXZ Hamiltonian
Frontiers of Physics (2022)
-
Realizing multi-qubit controlled nonadiabatic holonomic gates with connecting systems
AAPPS Bulletin (2022)



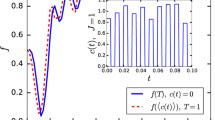


 in the presence of the flip-angle error (red solid curve) and frequency detuning error (blue dashed curve).
in the presence of the flip-angle error (red solid curve) and frequency detuning error (blue dashed curve). and
and  .
.