Message passing variational autoregressive network for solving intractable Ising models

Abstract

Deep neural networks have been used to solve Ising models, including autoregressive neural networks, convolutional neural networks, recurrent neural networks, and graph neural networks. Learning probability distributions of energy configuration or finding ground states of disordered, fully connected Ising models is essential for statistical mechanics and NP-hard problems. Despite tremendous efforts, neural network architectures with abilities to high-accurately solve these intractable problems on larger systems remain a challenge. Here we propose a variational autoregressive architecture with a message passing mechanism, which effectively utilizes the interactions between spin variables. The architecture trained under an annealing framework outperforms existing neural network-based methods in solving several prototypical Ising spin Hamiltonians, especially for larger systems at low temperatures. The advantages also come from the great mitigation of mode collapse during training process. Considering these difficult problems to be solved, our method extends computational limits of unsupervised neural networks to solve combinatorial optimization problems.

Introduction

Many deep neural networks have been used to solve Ising models^1,2, including autoregressive neural networks^3,4,5,6,7,8, convolutional neural networks⁹, recurrent neural networks^4,10, and graph neural networks^{11,12,13,14,15,16,17}. The autoregressive neural networks model the distribution of high-dimensional vectors of discrete variables to learn the target Boltzmann distribution^18,19,20,21 and allow for direct sampling from the networks. However, recent works question the sampling ability of autoregressive models in highly frustrated systems, with the challenge resulting from mode collapse^22,23. The convolutional neural networks⁹ respect the lattice structure of the 2D Ising model and achieve good performance³, but cannot solve models defined on non-lattice structures. Variational classical annealing (VCA)⁴ uses autoregressive models with recurrent neural networks (RNN)¹⁰ and outperforms traditional simulated annealing (SA)²⁴ in finding ground-state solutions to Ising problems. This advantage comes from the fact that RNN can capture long-range correlations between spin variables by establishing connections between RNN cells in the same layer. Those cells need to be computed sequentially, which results in a very inefficient computation of VCA. Thus, in a particularly difficult class of fully connected Ising models, Wishart planted ensemble (WPE)²⁵, ref. ⁴ only solves problem instances with up to 32 spin variables. Since a Hamiltonian with the Ising form can be directly viewed as a graph, it is intuitive to use graph neural networks (GNN)^26,27,28 to solve it. While a GNN-based method¹⁶ has been employed in combinatorial optimization problems with system sizes up to millions, which first encodes problems in Ising forms²⁹ and then relaxes discrete variables into continuous ones to use GNN, some researchers argue that this method does not perform as well as classical heuristic algorithms^30,31. In fact, the maximum cut and maximum independent set problem instances with millions of variables used in ref. ¹⁶ are defined on very sparse graphs and are not hard to solve³¹. Also, a naive combination of graph convolutional networks (GCN)²⁸ and variational autoregressive networks (VAN)³ (we denote it as ‘GCon-VAN’ in this work) is tried but performs poorly in statistical mechanics problems defined on sparse graphs⁸. Reinforcement learning has also been used to find the ground state of Ising models^32,33. In addition, recently developed Ising machines have been used to find the ground state of Ising models and have shown impressive performance³⁴, especially those based on physics-inspired algorithms, such as SimCIM (simulated coherent Ising machine)^35,36 and simulated bifurcation (SB)^37,38.

Exploration of new methods to tackle Ising problems of larger scale and denser connectivity is of great interest. For example, finding the ground states of Ising spin glasses on two-dimensional lattices can be exactly solved in polynomial time, while ones in three or higher dimensions are a non-deterministic polynomial-time (NP) hard problem³⁹. Ising models correspond to some problems defined on graphs, such as the maximum independent set problems, whose difficulty in finding the ground state might depend on the node’s degree being larger than a certain value^40,41. The design of neural networks to solve Ising models on denser graphs would lead to the development of powerful optimization tools and further shed light on the computational boundary of deep-learning-assisted algorithms.

Due to the correspondence between Ising models and graph problems, existing Ising-solving neural network methods can be described by the message passing (MP) neural networks (MPNN) framework⁴². MPNN can be used to abstract commonalities between them and determine the most crucial implementation details, which help to design more complex and powerful network architectures. Therefore, we reformulate existing VAN-based network architectures into this framework and then explore more variants for designing new network architectures with meticulously designed MP mechanisms to better solve intractable Ising models. Here, we propose a variational autoregressive architecture with a MP mechanism and dub it a message passing variational autoregressive network (MPVAN). It can effectively utilize the interactions between spin variables, including whether there are couplings and coupling values, while previous methods only considered the former, i.e., the correlations.

We show the residual energy histogram on the Wishart planted ensemble (WPE)²⁵ with a rough energy landscape in Fig. 1. Compared to VAN³, VCA⁴, and GCon-VAN⁸, the configurations sampled from MPVAN are concentrated on the regions with lower energy. Therefore, MPVAN has a higher probability of obtaining low-energy configurations, which is beneficial for finding the ground state, and it is also what combinatorial optimization is concerned about.

Fig. 1: The residual energy histogram of configurations sampled from networks after training.

The histogram is on the Wishart planted ensemble with system size N = 60 and difficulty parameter α = 0.2, which makes problem instances hard to solve. The residual energy is defined as the difference between the energy of the configurations sampled directly from the network after training and the energy of the ground state. Each method contains 9 × 10⁶ configurations obtained from 30 instances and each for 30 runs.

Numerical experiments show that our method outperforms the recently developed autoregressive network-based methods VAN and VCA in solving two classes of disordered, fully connected Ising models with extremely rough energy landscapes, the WPE²⁵ and the Sherrington–Kirkpatrick (SK) model⁴³, including more accurately estimating the Boltzmann distribution and calculating lower free energy at low temperatures. The advantages also come from the great delay in the emergence of mode collapse during the training process of deep neural networks. Moreover, as the system size increases or the connectivity of graphs increases, MPVAN has greater advantages over VAN and VCA in giving a lower upper bound to the energy of the ground state and thus can solve problems of larger sizes inaccessible to the methods reported previously. Besides, with the same number of samples (which is via the forward process of the network for MPVAN and which is via Markov chain Monte Carlo for SA/parallel tempering (PT)^{44,45,46,47,48,49}), MPVAN outperforms classical heuristics SA and performs similarly or slightly better than advanced PT in finding the ground state of the extremely intractable WPE and SK model. Compared to short-range Ising models such as the Edwards–Anderson model⁵⁰, infinite-ranged interaction models (SK model and WPE) we considered are more challenging since there exist many loops of different lengths, which leads to more complicated frustrations. Considering these extremely difficult problems to be solved, our method extends the current computational limits of unsupervised neural networks⁵¹ to solve intractable Ising models and combinatorial optimization problems⁵².

Methods

The message passing variational autoregressive network (MPVAN) is to solve Ising models with the Hamiltonian as

$$H=-\sum\limits_{\langle i,j\rangle }{J}_{ij}{s}_{i}{s}_{j},$$

(1)

where ${\{{s}_{i}\}}_{i = 1}^{N}\in {\{\pm 1\}}^{N}$ are N spin variables, and 〈i, j〉 denotes that there is a non-zero coupling J_ij between s_i and s_j.

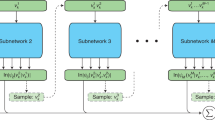
MPVAN is composed of an autoregressive MP mechanism and a variational autoregressive network architecture, and its network architecture is shown in Fig. 2a. The input to MPVAN is a configuration ${{{{{{{\bf{s}}}}}}}}={\{{s}_{i}\}}_{i = 1}^{N}$ in a predetermined order of spins, and the i_th component of the output, ${\hat{s}}_{i}$, means the conditional probability of s_i taking + 1 when given values of spins in front of it, s_<i, i.e., ${\hat{s}}_{i}={q}_{\theta }({s}_{i}=+1| {{{{{{{{\bf{s}}}}}}}}}_{ < i})$.

Fig. 2: Schematic of the network architecture of the message passing variational autoregressive network and four autoregressive message passing mechanisms.

The schematic is shown on a problem instance with 3 edges and 4 spins, where the spins are represented separately with numbers 1 to 4, and node features are represented separately with h_i, i = 1, 2, 3, 4. a The network architecture of the message passing variational autoregressive network (MPVAN). The spin configuration s = {±1}^N is the input to the network, $\hat{{{{{{{{\bf{s}}}}}}}}}$ is the output, and h denotes the hidden layer. The 〈s〉_MP and 〈h〉_MP are updated from s and h by message passing, respectively. The brown solid arrow indicates that neighboring nodes participate in message passing, while the brown dashed arrow indicates that there are connections between neighboring nodes but message passing is not performed to preserve the autoregressive property. The coefficients {a_ij} in the message passing process vary for different message passing mechanisms. b The processes of four autoregressive message passing (MP) mechanisms when updating h₃. Under the MP mechanism used in the variational autoregressive network (VAN)³, message passing is not performed, which is equivalent to the identity transformation of h₃. Under the MP mechanism used in GCon-VAN⁸, message passing performs according to the adjacency matrix A, which updates the h₃ based on the topology structure of the graph. For the Graph MP mechanism we designed, message passing is performed by using the couplings J_ij of the Hamiltonian, which updates h₃ based on the couplings and Z₃ = ∣J₃₁∣ + ∣J₃₂∣. The Hamiltonians MP mechanism we designed updates h₃ based on the couplings and values of neighboring spins s₁ and s₂, which is also the message passing mechanism used in MPVAN.

As in VAN³, the variational distribution of MPVAN is decomposed into the product of conditional probabilities as

$${q}_{\theta }({{{{{{{\bf{s}}}}}}}})=\prod\limits_{i=1}^{N}{q}_{\theta }({s}_{i}| {s}_{1},{s}_{2},\ldots ,{s}_{i-1}),$$

(2)

where q_θ(s) represents the variational joint probability and q_θ(s_i∣s₁, s₂, …, s_i−1) denotes the variational conditional probability, both of which are parametrized by trainable parameters θ.

MPVAN layer

MPVAN are constructed by stacking multiple messages passing variational autoregressive network layers. A single MPVAN layer is composed of an autoregressive MP process and nonlinear functions with trainable parameters defined by VAN³.

The input to the MPVAN layer is a set of node features, ${{{{{{{\bf{h}}}}}}}}=\{{\overrightarrow{h}}_{1},{\overrightarrow{h}}_{2},\ldots ,{\overrightarrow{h}}_{N}\},{\overrightarrow{h}}_{i}\in {(0,1)}^{F}$, where F is the number of training samples. The layer produces a new set of node features, ${{{{{{{{\bf{h}}}}}}}}}^{o}=\{{\overrightarrow{h}}{_{1}^{o}},{\overrightarrow{h}}{_{2}^{o}},\ldots ,{\overrightarrow{h}}{_{N}^{o}}\},{\overrightarrow{h}}{_{i}^{o}}\in {{\mathbb{R}}}^{F}$, as the output. For brevity, we set F = 1 and donate ${\overrightarrow{h}}_{i}$ and ${\overrightarrow{h}}{_{i}^{o}}$ as h_i and ${h}_{i}^{o}$, respectively. The h^o is obtained by

$${{{{{{{{\bf{h}}}}}}}}}^{o}=\sigma ({\langle {{{{{{{\bf{h}}}}}}}}\rangle }_{MP}W+b),$$

(3)

where sigmoid activation function $\sigma (x)=\frac{1}{1+{e}^{-x}}$ ranging in (0, 1) and thus ${h}_{i}^{o}\in (0,1)$. The ${\langle {{{{{{{\bf{h}}}}}}}}\rangle }_{MP}=\{{\langle {h}_{1}\rangle }_{MP},{\langle {h}_{2}\rangle }_{MP},\ldots ,{\langle {h}_{N}\rangle }_{MP}\}$, ${\langle {h}_{i}\rangle }_{MP}\in {\mathbb{R}}$, denotes the updated node features from h by MP. The W and b are layer-specific trainable parameters, and W is a triangular matrix to ensure the autoregressive property^3,19,20,21.

To show how to get 〈h〉_MP, we first review the MP mechanism defined in the MPNN framework⁴². We describe MP operations on the current layer with node features h_i and edge features J_ij. The MP phase includes how to obtain neighboring messages m_i and how to update node features h_i, which are defined as

$${m}_{i} =\, \sum\limits_{j\in {N}_{a}(i)}M({h}_{i},{h}_{j},{J}_{ij}),\\ {\langle {h}_{i}\rangle }_{MP} =U({h}_{i},{m}_{i}),$$

(4)

where h_j is the node feature of j, and

$${N}_{a}(i)=\{\,j\,| \,j \, < \, i,{J}_{ij} \,\ne\, 0\},$$

(5)

which denotes the neighbors located before node i. The N_a(i) is used to preserve autoregressive property, which is different from general MP mechanisms⁴² and graph neural networks^28,53,54. The message aggregation function M(h_i, h_j, J_ij) and node feature update function U(h_i, m_i) are different across MP mechanisms.

Now, existing autoregressive network-based methods can be reformulated into combinations of VAN and different MP mechanisms. Then, we explore their variants and propose our method.

In VAN³, there is no MP process from neighboring nodes. Therefore, the node features h_i are updated according to

$$\begin{array}{l}{m}_{i}=0,\\ {\langle {h}_{i}\rangle }_{MP}={h}_{i},\end{array}$$

(6)

which is the first MP mechanism in Fig. 2b. Another impressive variational autoregressive network approach is variational classical annealing (VCA)⁴, which uses the dilated RNN architecture⁵⁵ to take into account the correlations between hidden units in the same layer. VCA cannot be represented as a special MPVAN since the MP mechanisms for utilizing features of neighboring nodes are free of trainable parameters, which are different from the ones in VCA.

In GCon-VAN⁸, a combination of GCN²⁸ and VAN, the ${\langle {h}_{i}\rangle }_{MP}$ are obtained by

$${m}_{i} =\, \sum\limits_{j\in {N}_{a}(i)}{A}_{ij}{h}_{j},\\ {\langle {h}_{i}\rangle }_{MP} =\, \frac{{m}_{i}+{h}_{i}}{deg(i)+1},$$

(7)

where A is the adjacency matrix of the graph, and deg(i) represents the degree of node i. The h_i is updated based on the connectivity of the graph, which is the second MP mechanism in Fig. 2b.

However, GCon-VAN performs poorly on sparse graphs in calculating physical quantities such as correlations and free energy⁸ and it performs even worse on dense graphs in our trial. It may be because GCon-VAN only considers connectivity and ignores the weights of neighboring node features. Also, from the results of VAN in Fig. 1, the node feature h_i itself should be highlighted rather than the small weight $\frac{1}{deg(i)+1}$ in Eq. (7).

Therefore, we explore more variants and propose three MP mechanisms. The m_i are obtained by

$${m}_{i}=\sum\limits_{j\in {N}_{a}(i)}| {J}_{ij}| {h}_{j},$$

(8a)

$${m}_{i}=\sum\limits_{j\in {N}_{a}(i)}{J}_{ij}{h}_{j},$$

(8b)

$${m}_{i}=\sum\limits_{j\in {N}_{a}(i)}{J}_{ij}{s}_{j}{h}_{j}^{{\prime} },$$

(8c)

where

$${h}_{j}^{{\prime} }=\frac{1+{s}_{j}}{2}{h}_{j}+\frac{1-{s}_{j}}{2}(1-{h}_{j}).$$

(9)

In above three mechanisms, the ${\langle {h}_{i}\rangle }_{MP}$ are obtained by

$${\langle {h}_{i}\rangle }_{MP}=\frac{{m}_{i}}{{\sum }_{j\in {N}_{a}(i)}| {J}_{ij}| }+{h}_{i}.$$

(10)

For the neighboring message m_i in Eq. (8a), we consider the weight of neighboring node features instead of averagely passing those features in Eq. (7). Also, we increase the weight of h_i in Eq. (10) for all mechanisms we designed. However, the Eq. (8a) ignores the influence of the sign of couplings {J_ij}.

Thus, we propose the MP mechanism made of Eq. (8b) and Eq. (10), which is the third MP mechanism in Fig. 2b. It uses the values of couplings {J_ij} in the Hamiltonian to weight the neighboring node features. Since it is based on the graph defined by the target Hamiltonian, we dub it ‘graph MP mechanism’ (Graph MP).

Previous methods and the above two MP mechanisms we designed do not make full use of the interactions between spin variables of the Hamiltonian in Eq. (1), and known values of s_<i when updating the h_i. Intuitively, it may be helpful to consider those interactions and values of s_<i in the MP process.

Therefore, we propose the Hamiltonians MP mechanism composed of Eq. (8c) and Eq. (10), which is the fourth MP mechanism in Fig. 2b and also the mechanism used in MPVAN. The s_j = ± 1 is the known value of the neighboring spin j, and ${h}_{j}^{{\prime} }\in (0,1)$ represents the probability of the spin j taking s_j.

Based on the above definitions, it is reasonable to use ${h}_{j}^{{\prime} }$ rather than h_j in MP. To illustrate, suppose for the neighboring spin j, s_j = − 1 and h_j = 0.2. Then, if we repeatedly sample spin j, we could obtain s_j = − 1 with a probability of 0.8. It means that neighboring spin j should have a greater impact on h_i when it takes − 1 than + 1, but h_j = 0.2 is not as good as ${h}_{j}^{{\prime} }=0.8$ to reflect the great importance of s_j = − 1. On the other hand, suppose for the neighboring spin j, s_j = − 1 and h_j = 0.8. We could obtain s_j = − 1 with a probability of 0.2 if we sample spin j again. At this time, using ${h}_{j}^{{\prime} }$ instead of h_j could show little importance of s_j = − 1. So we think it makes sense to use ${h}_{j}^{{\prime} }$ to reflect the effect of the spin j taking s_j in MP.

Taking the graph with 4 nodes and 3 edges in Fig. 2b as an example, applying the above four MP mechanisms, the ${\langle {h}_{3}\rangle }_{MP}$ are obtained as

$${\langle {h}_{3}\rangle }_{MP\,in\,VAN}={h}_{3},$$

(11a)

$${\langle {h}_{3}\rangle }_{MP\,in\,GCon-VAN}=\frac{{h}_{1}+{h}_{2}+{h}_{3}}{3},$$

(11b)

$${\langle {h}_{3}\rangle }_{{{{{{\rm{Graph}}}}}}\,MP}=\frac{{J}_{31}{s}_{1}{h}_{1}+{J}_{32}{s}_{2}{h}_{2}}{| {J}_{31}| +| {J}_{32}| }+{h}_{3},$$

(11c)

$${\langle {h}_{3}\rangle }_{{{{{{\rm{Hamiltonians}}}}}}\,MP}=\frac{{J}_{31}{s}_{1}{h}_{1}^{{\prime} }+{J}_{32}{s}_{2}{h}_{2}^{{\prime} }}{| {J}_{31}| +| {J}_{32}| }+{h}_{3}.$$

(11d)

We also consider more MP mechanisms and compare their performance in Supplementary Note I, where Hamiltonians MP always performs best. In addition, since an arbitrary MP variational autoregressive network is constructed through stacking MPVAN layers, we also discuss the effect of the number of layers on the performance. MPVAN exhibits characteristics similar to GNN, i.e., there exists an optimal number of layers, which can be found in Supplementary Note II.

Training MPVAN

We then describe how to train MPVAN. In alignment with the variational approach employed in VAN, the variational free energy F_q is used as loss function,

$${F}_{q}=\sum\limits_{{{{{{{{\bf{s}}}}}}}}}{q}_{\theta }({{{{{{{\bf{s}}}}}}}})\left[E({{{{{{{\bf{s}}}}}}}})+\frac{1}{\beta }\ln {q}_{\theta }({{{{{{{\bf{s}}}}}}}})\right],$$

(12)

where β = 1/T is inverse temperature, and E(s) is the H of Eq. (1) related to a given configuration s. The configuration s follows Boltzmann distribution p(s) = e^−βE(s)/Z, where Z = ∑_se^−βE(s). Since the Kullback–Leibler (KL) divergence between the variational distribution q_θ and the Boltzmann distribution p is defined as ${D}_{KL}({q}_{\theta }| | p)={\sum }_{{{{{{{{\bf{s}}}}}}}}}{q}_{\theta }({{{{{{{\bf{s}}}}}}}})\ln (\frac{{q}_{\theta }({{{{{{{\bf{s}}}}}}}})}{p({{{{{{{\bf{s}}}}}}}})})=\beta ({F}_{q}-F)$ and is always non-negative, F_q is the upper bound to the free energy $F=-(1/\beta )\ln Z$.

The gradient of F_q with respect to the parameters θ is

$${\bigtriangledown }_{\theta }{F}_{q}=\sum\limits_{{{{{{{{\bf{s}}}}}}}}}{q}_{\theta }({{{{{{{\bf{s}}}}}}}})\left\{\left[E({{{{{{{\bf{s}}}}}}}})+\frac{1}{\beta }\ln {q}_{\theta }\left.({{{{{{{\bf{s}}}}}}}})\right)\right]{\bigtriangledown }_{\theta }\ln {q}_{\theta }({{{{{{{\bf{s}}}}}}}})\right\}.$$

(13)

With the computed gradients ▽_θF_q, we iteratively adjust the parameters of the networks until the F_q stops decreasing.

MPVAN is trained under an annealing framework, i.e., starting from the initial inverse temperature β_initial and gradually decreasing the temperature by annealing N_annealing steps until the end temperature β_final. We linearly increase the inverse temperature with a step of β_inc. During each annealing step, we decrease the temperature and subsequently apply N_training gradient-descent steps to update the network parameters using Adam optimizer⁵¹, thereby minimizing the variational free energy F_q. As with the VAN³, the network is trained using the data produced by itself, and at each training step, N_samples samples are drawn from the networks for training. After training, we can sample directly from the network to calculate the upper bound to the free energy and other physical quantities such as entropy and correlations.

Theoretical analysis for MPVAN

Compared to VAN³, MPVAN has an additional Hamiltonians MP process. In this section, we will provide a theoretical and mathematical analysis of the advantages of the Hamiltonians MP mechanism in MPVAN in Corollary 1 below.

The goal of MPVAN is to be able to accurately estimate the Boltzmann distribution, i.e., configurations with low energy have a high probability and configurations with high energy have a low probability. Specifically, MPVAN is trained by minimizing the variational free energy F_q, composed of ${{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}E({{{{{{{\bf{s}}}}}}}})$ and ${{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}\ln {q}_{\theta }({{{{{{{\bf{s}}}}}}}})$.

Corollary 1

The Hamiltonians MP process makes ${{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}E({{{{{{{\bf{s}}}}}}}})$ and ${{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}\ln {q}_{\theta }({{{{{{{\bf{s}}}}}}}})$ smaller, and therefore variational free energy F_q smaller compared to no MP.

Proof

We discuss MP process that makes ${{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}E({{{{{{{\bf{s}}}}}}}})$ and ${{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}\ln {q}_{\theta }({{{{{{{\bf{s}}}}}}}})$ smaller separately.

Step 1: Making ${{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}E({{{{{{{\bf{s}}}}}}}})$ smaller.

When training MPVAN, it is impossible to exhaust all configurations to calculate the variational free energy F_q, so we use the mathematical expectation of training samples to estimate it. Therefore, we have

$${{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}E({{{{{{{\bf{s}}}}}}}})=\frac{1}{{N}_{samples}}\sum\limits_{k=1}^{{N}_{samples}}E({{{{{{{{\bf{s}}}}}}}}}_{k}),$$

(14)

where s_k is k_th training samples and N_samples is the number of training samples.

Consider the Hamiltonians MP process (composed of Eq. (8c) and Eq. (10)) for updating the h_i as an example to analyze how MP makes ${{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}E({{{{{{{\bf{s}}}}}}}})$ smaller. Since the MP process maintains autoregressive property, making E(s) smaller for any configuration is equivalent to making the local Hamiltonian defined as H_local = − ∑_j<iJ_ijs_is_j smaller, when given the values of its neighboring spins s_<i.

Since H_local = − s_i∑_j<iJ_ijs_j with known ∑_j<iJ_ijs_j, we are concerned about how the MP affects the probability of s_i taking +1 or −1. According to Eq. (10), the value of ${\sum }_{j < i}{J}_{ij}{s}_{j}{h}_{j}^{{\prime} }$ plays an important role in that, and we discuss it in 2 cases.

Case 1: if ${\sum }_{j < i}{J}_{ij}{s}_{j}{h}_{j}^{{\prime} } \, > \, 0$, then according to Eq. (10), we have

$${\langle {h}_{i}\rangle }_{MP} \, > \, {h}_{i},$$

(15)

i.e.,

$$Pr[{\langle {s}_{i}\rangle }_{MP}=+1| {{{{{{{{\bf{s}}}}}}}}}_{ < i}] \, > \, Pr[{s}_{i}=+1| {{{{{{{{\bf{s}}}}}}}}}_{ < i}],$$

(16)

where

$${\langle {s}_{i}\rangle }_{MP}={{{{{\rm{Bernoulli}}}}}}({\langle {h}_{i}\rangle }_{MP}),$$

(17a)

$${s}_{i}={{{{{\rm{Bernoulli}}}}}}({h}_{i}).$$

(17b)

The Bernoulli(p) denotes sampling from the Bernoulli distribution to output +1 with a probability p. Thus, we have

$$Pr[{\langle {H}_{{{{{\rm{local}}}}}}^{{\prime} }\rangle }_{MP} \, < \, 0] \, > \, Pr[{H}_{{{{{\rm{local}}}}}}^{{\prime} } \, < \, 0],$$

(18)

where

$${\langle {H}_{{{{{\rm{local}}}}}}^{{\prime} }\rangle }_{MP}=-{\langle {s}_{i}\rangle }_{MP}\sum\limits_{j < i}{J}_{ij}{s}_{j}{h}_{j}^{{\prime} },$$

(19a)

$${H}_{{{{{\rm{local}}}}}}^{{\prime} }=-{s}_{i}\sum\limits_{j < i}{J}_{ij}{s}_{j}{h}_{j}^{{\prime} },$$

(19b)

and Pr[ ⋯  ] denotes the probability of something.

Case 2: if ${\sum }_{j < i}{J}_{ij}{s}_{j}{h}_{j}^{{\prime} } < 0$, then according to Eq. (10), we have

$${\langle {h}_{i}\rangle }_{MP} \, < \, {h}_{i},$$

(20)

i.e.,

$$Pr[{\langle {s}_{i}\rangle }_{MP}=-1| {{{{{{{{\bf{s}}}}}}}}}_{ < i}] \, > \, Pr[{s}_{i}=-1| {{{{{{{{\bf{s}}}}}}}}}_{ < i}],$$

(21)

and also obtain the Eq. (18). Therefore, regardless of the value of ${\sum }_{j < i}{J}_{ij}{s}_{j}{h}_{j}^{{\prime} }$, MP process always makes ${H}_{{{{{\rm{local}}}}}}^{{\prime} }$ smaller compared with no MP.

It can be found that the difference between H_local and ${H}_{{{{{\rm{local}}}}}}^{{\prime} }$ is that the latter has ${h}_{j}^{{\prime} }$. It encapsulates more information about the spin j beyond the current configuration spin value s_j, which can indicate how much influence the message corresponding to the neighboring node features h_j has on ${\langle {h}_{i}\rangle }_{MP}$ and, combining with the coupling J_ij, performs a weighted MP. Thus, although not identical, it is possible to predict H_local through ${H}_{{{{{\rm{local}}}}}}^{{\prime} }$ and thus we get the conclusion that Hamiltonians MP mechanism makes local Hamiltonian smaller.

Step 2: Making ${{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}\ln {q}_{\theta }({{{{{{{\bf{s}}}}}}}})$ smaller.

Similar to ${{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}E({{{{{{{\bf{s}}}}}}}})$, we have

$${{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}\ln {q}_{\theta }({{{{{{{\bf{s}}}}}}}})=\frac{1}{{N}_{{{{{\rm{samples}}}}}}}\sum\limits_{k=1}^{{N}_{{{{{\rm{samples}}}}}}}\ln {q}_{\theta }({{{{{{{{\bf{s}}}}}}}}}_{k}).$$

(22)

The second derivative of $y(x)=\ln (x)$ is y(x)⁽²⁾ = −1/x² and thus y(x) is concave down, which satisfies $\frac{y(a)+y(b)}{2} < y(\frac{a+b}{2})$^56,57. From the analysis of Step 1, the MP process improves (reduces) the probability of configurations with low (high) energy. Therefore, MP makes ${\sum }_{k = 1}^{{N}_{{{{{\rm{samples}}}}}}}\ln {q}_{\theta }({{{{{{{{\bf{s}}}}}}}}}_{k})$ smaller compared to no MP. □

In summary, combining the analyses of Step 1 and Step 2, the MP process makes the variational free energy F_q smaller compared to no MP.

Results

Since Hamiltonians MP always performs best, as shown in Supplementary Note I, we only consider this MP mechanism in the following numerical experiments. In addition, for simplicity, we always use VCA to refer to VCA with the dilated RNN⁴.

We first experimented on the Wishart planted ensemble (WPE)²⁵. The WPE is a class of fully connected Ising models with an adjustable difficulty parameter α and two planted solutions that correspond to the two ferromagnetic states, which makes it an ideal benchmark problem for evaluating heuristic algorithms. The Hamiltonian of the WPE is defined as

$$H=-\frac{1}{2}\sum\limits_{i\ne j}{J}_{ij}{s}_{i}{s}_{j},$$

(23)

where the coupling matrix {J_ij} is a symmetric matrix and satisfies copula distribution. More details about the WPE can be found in ref. ²⁵.

First, we discuss an important issue, mode collapse, which occurs when the target probability distribution has multiple peaks but networks only learn a few of them. It severely affects the sampling ability of autoregressive neural networks²³. Entropy is commonly used in physics to measure the degree of chaos in a system. The greater the entropy, the more chaotic the system. Therefore, we can use the magnitude of entropy to reflect whether mode collapse occurs for the variational distribution. In our experiments, we investigate how the negative entropy, a part of variational free energy F_q in Eq. (12), changes during training, which is defined as

$$-S=\sum\limits_{{{{{{{{\bf{s}}}}}}}}}{q}_{\theta }({{{{{{{\bf{s}}}}}}}})\ln {q}_{\theta }({{{{{{{\bf{s}}}}}}}}),$$

(24)

where S is entropy. Equivalently, the smaller the negative entropy, the better the diversity of solutions.

As shown in Fig. 3, the change of −S from MPVAN shows an increasing-decreasing-increasing trend, while −S from other methods is monotonely increasing and quickly convergent. When training step ≥ 500, mode collapse occurs for other methods, while until training step ≥ 2000, it occurs for MPVAN. Therefore, MPVAN delays the emergence of mode collapse greatly. In addition, we also consider the impact of learning rates on the emergence of mode collapse in Supplementary Note X, where mode collapse always occurs later in MPVAN than in VAN.

Fig. 3: The negative entropy during training.

Note that annealing N_annealing = 25 steps and run N_training = 100 steps at each temperature, on an instance of the Wishart planted ensemble with N = 30, α = 0.2, and averaging on 10 runs.

Next, we benchmark MPVAN with existing methods when calculating the upper bound to the energy of the ground state, i.e., finding a configuration s to minimize the Hamiltonian in Eq. (23), which is also the core concern of combinatorial optimization. To facilitate a quantitative comparison, we employ the concept of residual energy, defined as

$${\epsilon }_{{{{{\rm{res}}}}}}={\left[{\left\langle {H}_{{{{{\rm{min}}}}}}\right\rangle }_{{{{{\rm{ava}}}}}}-{E}_{G}\right]}_{{{{{\rm{ava}}}}}},$$

(25)

where H_min represents the minimum value of the Hamiltonians corresponding to 10⁶ configurations sampled directly from the network after training, and E_G is the energy of the ground state. The ${\left\langle \ldots \right\rangle }_{{{{{\rm{ava}}}}}}$ denotes the average over 30 independent runs for one same instance, and ${\left[\ldots \right]}_{ava}$ means averaging on 30 instances. In Figs. 4 and 5, the solid line indicates the average value of the residual energy from 30 instances and each for 30 independent runs, and the color band indicates the area between the maximum and minimum values of the residual energy of 30 independent runs for the corresponding algorithm. Both solid lines and color bands are obtained by averaging 30 instances.

Fig. 4: The residual energy varies with system size on two fully connected Ising models.

a On the Wishart planted ensemble, the residual energy per site ϵ_res/N averages on 30 instances and each for 30 runs, all instances with the system size N and α = 0.2. When N ≥ 60, the problem instances cannot be solved due to rough energy landscapes. b On the Sherrington–Kirkpatrick model, the ϵ_res/N averages 30 instances and each for 10 runs. Since the energy of the ground state cannot be determined, we use the lowest energy across Message Passing Variational Autoregressive Network (MPVAN), Variational Autoregressive Network (VAN), Simulated Annealing (SA), and Parallel Tempering (PT) to replace it. Due to computational limitations, we exclude Variational Classical Annealing (VCA) from comparison when N > 100 as its speed is about N/10 times slower than MPVAN when trained under the same hyperparameters. More details regarding the computational speed of MPVAN, VAN, and VCA can be found in Supplementary Note V. Note that the solid line indicates the average value of the residual energy from 30 instances and each for 30 independent runs, and the color band indicates the area between the maximum and minimum values of the residual energy of 30 independent runs for the corresponding algorithm. Both solid lines and color bands are obtained by averaging 30 instances.

As in Fig. 4a, the residual energy obtained by our method consistently is lower than that of VAN, VCA, and SA across all system sizes when averaging 30 instances and each for 30 runs. Even compared with advanced parallel tempering (PT)^{44,45,46,47,48,49}, MPVAN also exhibits similar or slightly better performance in terms of average residual energy, and significantly better in terms of minimum residual energy. For WPE instances with system size N = 50, MPVAN can still find the ground state with non-ignorable probability, but other methods cannot. As the system size increases, MPVAN has greater advantages over VAN and VCA in giving a lower residual energy. Since the number of interactions between spin variables is ∣{J_ij ≠ 0}∣ = N² for fully connected systems, larger systems have many more interactions between spin variables. The advantages indicate that using MPVAN to consider these interactions performs better in rougher energy landscapes. We always average 30 instances to reflect the general properties of models, and the differences between instances can be seen in Supplementary Note I. Also, each method runs independently 30 times on the same instances to weaken the influence of occasionality in the heuristics training, which can be found in Supplementary Note III.

Since these methods are trained in different ways and on different hardware, we keep the total number of training samples used in training and final sampling after training the same for all methods to achieve a relatively fair comparison. For SA/PT, it is the number of Monte Carlo steps. The training samples of MPVAN consist of two parts, training samples and final sampling samples. Assuming annealing N_annealing times, training N_training steps at each temperature, sampling N_samples samples each step in training, and final sampling N_finsam samples, the total number of training samples for MPVAN is

$${N}_{{{{{{\rm{MPsam}}}}}}}={N}_{{{{{\rm{annealing}}}}}}\times {N}_{{{{{\rm{training}}}}}}\times {N}_{{{{{\rm{samples}}}}}}+{N}_{{{{{\rm{finsam}}}}}}.$$

(26)

The training samples for VAN and VCA are the same as those for MPVAN, with some fine-tuning of parameters. Assuming the number of inner loops of SA is N_inlop at each temperature, and the total number of training samples for SA is

$${N}_{{{{{\rm{SAsam}}}}}}={N}_{{{{{\rm{annealing}}}}}}\times {N}_{{{{{\rm{inlop}}}}}}.$$

(27)

Assuming the number of chains of PT is N_chain, and the Markov chain Monte Carlo iterations at each chain is N_MC, then the number of training samples for PT is

$${N}_{{{{{\rm{PTsam}}}}}}={N}_{{{{{\rm{chain}}}}}}\times {N}_{MC}.$$

(28)

Therefore, corresponding to 1 run of MPVAN, SA runs ⌈N_MPsam/N_SAsam⌉ times independently, and PT runs ⌈N_MPsam/N_PTsam⌉ times independently, and then they output their respective best results to benchmark MPVAN. For each benchmark algorithm, we have fine-tuned the training parameters to maximize its best performance. Moreover, we compare the time-to-target (TTT) metric commonly used in the hardware community. For finding the target values, MPVAN uses fewer iterations and training samples than PT, SA, VAN, and VCA, but it takes longer compared to PT. More results and details about the TTT metric can be found in Supplementary Note VI.

We also experiment on the Sherrington–Kirkpatrick (SK) model⁴³, which is one of the most famous fully connected spin glass models and has significant relevance in combinatorial optimization and machine learning applications^58,59. Its Hamiltonian is also in the form of Eq. (23), where each coupling J_ij is randomly generated from Gaussian distribution with the variance 1/N and the coupling matrix is symmetric.

As in Fig. 4b, our method provides significantly lower residual energy than VAN and SA across all system sizes when averaging 30 instances each for 10 runs. Notably, as the system size increases, the advantages of our method over VAN and SA become even more pronounced, which is consistent with the trend observed in WPE experiments. Compared to advanced PT, our method achieves close performance. We also show the approximating ratio results on the WPE and the SK model in Supplementary Note IV, which is of concern to researchers of combinatorial optimization problems. We also use discrete simulated bifurcation (dSB)³⁷, a physics-inspired Ising machine, as a benchmark algorithm to achieve a more comprehensive performance evaluation of MPVAN. MPVAN achieves higher accuracy than dSB for the same runtime on the WPE with N = 90 and the SK model with N = 300. It should be noted that dSB has a short single computation time and, therefore, has significant advantages in solving large-scale problems. More results and details about dSB can be found in Supplementary Note VII.

Inspired by the correlations between node’s degree and difficulty in finding the ground state in maximum independent set problems^40,41, in addition to experimenting on fully connected models, we also consider experiments on models with different connectivity, i.e., degrees of nodes in graphs. Since the SK model has been widely studied, designing models based on it may be meaningful. We construct models defined on graphs with different connectivity by deleting some couplings of the SK model and naming them variants of the SK model. Its Hamiltonian is in the form of Eq. (1), where each coupling J_ij is randomly generated from Gaussian distribution with the variance of 1/N and the coupling matrix is symmetric. At each degree, we always randomly generate 30 instances each for 10 runs. As shown in Fig. 5, our method gives a lower residual energy than VAN and SA at all degrees. Moreover, as the degree increases, the advantages of our method over VAN and SA become even more pronounced. The denser the graph, the larger the number of interactions between spin variables. The advantages show that our method, which takes into account these interactions, is able to give lower upper bounds to the free energy. Also, MPVAN achieved performance close to the advanced PT, and the poor performance of the PT on the sparsest problems used in this work may be related to the fact that the hyperparameters of the PT are not easy to choose at this time. More details about the PT implementation can be found in Supplementary Note VIII.

Fig. 5: The residual energy varies with the connectivity of graphs on non-fully connected Ising models.

The residual energy per site ϵ_res/N varies with the average degree of nodes in graphs on the variant of the Sherrington–Kirkpatrick model, with N = 200 averaging on 30 randomly generated instances and each for 10 runs. The solid lines and color bands are defined the same as in Fig. 4.

In the following, we focus on estimating the Boltzmann distribution and calculating the free energy as annealing. As a proof of concept, we use the WPE with a small system size of N = 20, where 2^N configurations can be enumerated, and the exact Boltzmann distribution and exact free energy F can be calculated within an acceptable time. We set α = 0.05, and thus it is difficult to find the ground state due to strong low-energy degeneracy.

As shown in Fig. 6, when the temperature is high, i.e., when β is small, the D_KL(q_θ∣∣p) and the relative errors of F_q relative to exact free energy F from MPVAN, VAN, and VCA are particularly small. Therefore, it is necessary to lower the temperature to distinguish them. As the temperature decreases, the probability of the configurations with low (high) energy in the Boltzmann distribution increases (decreases), thus making it more difficult for neural networks to estimate the Boltzmann distribution. However, we find that the D_KL(q_θ∣∣p) obtained by our method is much smaller than that of VAN and VCA, which indicates that the variational distribution q_θ(s) parameterized by our method is closer to the Boltzmann distribution. Similarly, our method gives a better estimation of free energy than VAN and VCA. These results illustrate that our method takes into account the interactions between spin variables through MP and is more accurate in estimating the relevant physical quantities.

Fig. 6: The Kullback–Leibler divergence and relative errors vary with inverse temperature.

The experiments are conducted on the Wishart planted ensemble with N = 20 and α = 0.05. a The Kullback–Leibler (KL) divergence D_KL(q_θ∣∣p) between the variational distribution q_θ and the Boltzmann distribution p. The inset shows the D_KL(q_θ∣∣p) when the inverse temperature β is small. b The relative errors (Rel. Err) of the variational free energy F_q relative to the exact free energy F. The inset shows the relative errors when β is small.

Conclusions

In summary, we propose a variational autoregressive architecture with a MP mechanism, which can effectively utilize the interactions between spin variables, to solve intractable Ising models. Numerical experiments show that our method outperforms the recently developed autoregressive network-based methods VAN and VCA in more accurately estimating the Boltzmann distribution and calculating lower free energy at low temperatures on two fully connected and intractable Ising spin Hamiltonians, WPE, and the SK model. The advantages also come from the great mitigation of mode collapse during the training process of deep neural networks. Moreover, as the system size increases or the connectivity of graphs increases, MPVAN has greater advantages over VAN and VCA in giving a lower upper bound to the energy of the ground state and thus can solve problems of larger sizes inaccessible to the methods reported previously. Besides, with the same number of samplings (which is via the forward process of the network for MPVAN and which is via Markov chain Monte Carlo for SA/PT), MPVAN outperforms classical heuristics SA and performs similarly or slightly better than advanced PT in finding the ground state of the extremely intractable WPE and SK model, which illustrates the enormous potential of autoregressive networks in solving Ising models and combinatorial optimization problems.

Formally, MPVAN and GNN are similar. We notice that some researchers have recently argued that graph neural networks do not perform as well as classical heuristic algorithms on combinatorial optimization problems^30,31 for the method in ref. ¹⁶. Our work, however, draws the opposite conclusion. We argue that when the problems are in rough energy landscapes and hard to find the ground state (e.g., WPE), our method performs significantly better than traditional heuristic algorithms such as SA and even similarly or slightly better than advanced PT. Our method is based on variational autoregressive networks, which are difficult to train due to slow speed when the systems are particularly large, and thus MPVAN is not easy to expand to very large problems. At the very least, we argue that MPVAN (or GNN) excels particularly well in certain intractable Ising models with rough energy landscapes and finite size, providing an alternative to traditional heuristics.

Theoretically, being the same with VAN, the computational complexity of MPVAN is O(N²), due to the nearly fully connected relationship between neighboring hidden layers when dealing with fully connected models, while VCA with dilated RNNs is $O(N\log (N))$. It might be interesting to explore how to reduce the computational complexity of MPVAN. In algorithm implementation, hidden units from the same layer in MPVAN can be computed at once, while hidden units in VCA must be computed sequentially due to the properties of the RNN architecture. More details about the computational speed of MPVAN, VAN, and VCA can be found in Supplementary Note V.