Abstract
Topological flat bands — where the kinetic energy of electrons is quenched — provide a platform for investigating the topological properties of correlated systems. Here, we report the observation of a topological flat band formed by polar-distortion-assisted Rashba splitting in the three-dimensional Dirac material ZrTe5. The polar distortion and resulting Rashba splitting on the band are directly detected by torque magnetometry and the anomalous Hall effect, respectively. The local symmetry breaking further flattens the band, on which we observe resistance oscillations beyond the quantum limit. These oscillations follow the temperature dependence of the Lifshitz–Kosevich formula but are evenly distributed in B instead of 1/B at high magnetic fields. Furthermore, the cyclotron mass gets anomalously enhanced about 102 times at fields ~ 20 T. Our results provide an intrinsic platform without invoking moiré or order-stacking engineering, which opens the door for studying topologically correlated phenomena beyond two dimensions.
Similar content being viewed by others
Introduction
Flat electronic bands harbor exotic quantum behaviors due to the quenched kinetic energy and subsequently dominated Coulomb interaction. The fractional quantum Hall effect1,2 is an archetypical two-dimensional (2D) flat band system. Recently developed moiré-engineered 2D twisted bilayer graphene3,4,5 and multilayer graphene in certain stacking order6,7,8 are other examples of realizing topological flat bands. Flat bands are also theoretically predicted in some stoichiometric three-dimensional (3D) materials forced by certain geometric lattices, like the kagome or Lieb lattices9,10. Flat band-induced correlation in 3D topological systems is crucial for realizing correlated 3D topological effects, like correlation on Weyl semimetals (WSM) and possible axionic dynamics11,12,13. Despite theoretical advancement in establishing the material database of topological flat bands14, experimental realization of an isolated topological flat band around Fermi level (FL) in 3D stoichiometric materials remains elusive.
In the twisted bilayer graphene, the two preconditions for realizing a 2D topological flat band are: 1. the pristine Dirac material graphene; 2. moiré superlattice as the method for flattening the band. We now ask a question: can we find a counterpart in 3D? If there is, then which material is the 3D counterpart of graphene? How do we flatten the energy band or enlarge the unit cell in 3D? Here, we report that ZrTe515, as a typical Dirac material in 3D, can meet the first precondition; the polar distortion at low temperatures in ZrTe5 meets the second precondition without invoking van der Waals heterostructure-based engineering. The polar distortion-assisted Rashba splitting in ZrTe5 is evidenced by torque magnetometry and the anomalous Hall effect (AHE), which shows the existence of a topological flat band in the magnetic field, on which anomalous resistance oscillations appear beyond the quantum limit. The cyclotron mass is enhanced by an order of 102, consistent with the topological flat band. Our work also highlights the importance of local symmetry breaking in topological materials.
Results
Rashba splittings and anomalous Hall effect in ZrTe5
ZrTe5 was initially proposed as a typical candidate for a quantum spin Hall insulator in 2D limit15. As shown in Fig. 1a, 2D ZrTe5 layers stack along b axis (here, we use a, b, c and -x, z, y interchangeably) with a ZrTe3 chain that runs along a axis. The topological property of 3D ZrTe5 is sensitively dependent on the inter- and intra-layer coupling strengths. ZrTe5 is located near the boundary of weak topological (WTI) and strong topological insulators (STI) as typical Dirac material15, promoting many exotic phenomena16,17,18,19,20,21,22. Therefore, the properties of ZrTe5 are sensitively dependent on crystal growth methods, namely the chemical vapor transfer (CVT) and flux processes. Samples grown from Te-flux are more stoichiometric and closer to the phase boundary23,24,25,26. As shown in Fig. 1b, temperature-dependent resistivity measured on flux-grown single crystals (see Supplementary Fig. 1 for more detailed characterizations of single crystals) exhibits semiconducting-like behavior, a typical profile in narrow-gapped semiconductors27,28. We focus on electrical transport within ac plane with current i along a axis as illustrated in the inset of Fig. 1b. Hall measurements (Fig. 1c) show that hole is the only carrier down to 2 K. Hall conductivity \({\sigma }_{{xy}}\) (Fig. 1d) fitted by Drude model \({\sigma }_{{xy}}^{{{{{{\rm{Drude}}}}}}}=\frac{{pe}{\mu }^{2}{{{{{\rm{B}}}}}}}{1+{\mu }^{2}{{{{{{\rm{B}}}}}}}^{2}}\), where p is the carrier density and \(\mu\) is the mobility, shows the existence of an anomalous term \({\sigma }_{{xy}}^{A}\), as indicated by the pink shadowed area (see Supplementary Fig. 2 for more details on the Drude fittings). As shown in Fig. 1e, p is ultralow ~ 3\(\times\)1014 cm−3 and \(\mu\) is as high as 106 cm2 V−1 s−1 at low temperatures, crucial for realizing the topological flat band and anomalous resistance oscillations. Therefore, ZrTe5 sample synthesized in this work is a 3D counterpart of graphene.
a Crystal structure of undistorted ZrTe5. b Temperature-dependent resistivity \({\rho }_{{xx}}\) of typical flux-grown ZrTe5 samples measured in this work. The inset shows an image of a typical device with patterned Au electrodes. c Temperature-dependent Hall resistivity \({\rho }_{{yx}}\) of sample S75. Anomalous term develops when the temperature is low. d Temperature-dependent Hall conductivity \({\sigma }_{{xy}}\) converted from \({\rho }_{{yx}}\). The anomalous term \({\sigma }_{{xy}}^{A}\), shadowed by the pink area, occurs after the Drude subtraction (dashed line). e Temperature-dependent carrier density (p) and mobility (\(\mu\)) of sample S75.
a Angle-dependent magnetic torque at 7 T measured at different temperatures. The inset illustrates the experimental setup. The solid black line shows the fitting by the formula \({{{{{{\boldsymbol{\tau }}}}}}}_{a}={A}_{1}\sin 2\theta+\) \({A}_{2}{\sin }^{2}\theta\), where \({A}_{1}\) represents the orthorhombic structure and \({A}_{2}\) represents the lower-symmetric structure. b Temperature-dependent anomalous Hall conductivity \({\sigma }_{{xy}}^{A}\) obtained after subtracting the Drude component. \({B}_{p}\) is defined as a critical magnetic field of the onset of plateau-like structure on \({\sigma }_{{xy}}^{A}\). c Temperature-dependent \({A}_{{{{{\mathrm{1,2}}}}}}(T)/{A}_{{{{{\mathrm{1,2}}}}}}(270{K})\) and \({\sigma }_{{xy}}^{A}\) in sample S75. \({A}_{{{{{\mathrm{1,2}}}}}}(T)\) denotes \({A}_{1}\) and \({A}_{2}\). The dashed vertical pink line indicates the concurrence of \({\sigma }_{{xy}}^{A}\) and polar distortion. d Illustration of band modifications in the presence of polar distortion. The left-hand column shows the magnetic field-induced gap in the original Rashba bands, and finally, a local topological flat band is formed at the top of the band in a higher magnetic field. The right-hand column shows the flatness is strongly enhanced by the local symmetry breaking promoted by polar distortions.
We then investigate the possible local modifications on the Dirac band, which might provide the clue for forming a topological flat band. In these flux-grown samples, preliminary evidence of polar distortion is reported by nonlinear transport26, while direct evidence is still lacking. We adopted torque magnetometry to measure the magnetic susceptibility tensor \({\chi }_{{ij}}\) defined by \({{{{{{\bf{M}}}}}}}_{i}={\chi }_{{ij}}{{{{{{\bf{H}}}}}}}_{j}\), where \({{{{{{\bf{M}}}}}}}_{i}\) is the magnetization. \({\chi }_{{ij}}\) directly reflects the underlying point group symmetries due to Neumann’s principle. Magnetic torque is defined as\(\,{{{{{\boldsymbol{\tau }}}}}}={\mu }_{0}V{{{{{\bf{M}}}}}}\times {{{{{\bf{H}}}}}}\), where \({\mu }_{0}\) is the vacuum permeability, and \(V\) is the volume of the sample. The space group of ZrTe5 is \({Cmcm}\) (No. 63) with a point group \({D}_{2h}\), under which the only permitted tensor elements in \({\chi }_{{ij}}\) are \({\chi }_{{aa}},{\chi }_{{cc}}\) and \({\chi }_{{bb}}\). In our torque setup (inset of Fig. 2a), the cantilever picks up \({{{{{{\boldsymbol{\tau }}}}}}}_{a\left(x\right)}={{{{{{\boldsymbol{\tau }}}}}}}_{2\theta }={A}_{1}\sin 2\theta\), where \({A}_{1}=\frac{1}{2}{\mu }_{0}V{{{{{{\rm{H}}}}}}}^{2}\left({\chi }_{{cc}}-{\chi }_{{bb}}\right)\). Therefore, we anticipate a pure \(\sin 2\theta\) relation in angle-dependent \({{{{{{\boldsymbol{\tau }}}}}}}_{a}\). As shown in Fig. 2a, \({\tau }_{a}\) at 7 T globally shows \(\pi\) periodicity consistent with \(\sin 2\theta\) relation. However, the negative and positive amplitudes, noted as Amp+ and Amp− in Fig. 2a, show asymmetry against a pure \(\sin 2\theta\) relation, which is absent in a CVT sample (see Supplementary Fig. 3b and Supplementary Note 1). Further, we find the torque signal at 4 K can be well fitted by \({{{{{{\boldsymbol{\tau }}}}}}}_{a}={{{{{{\boldsymbol{\tau }}}}}}}_{2\theta }+\) \({A}_{2}{\sin }^{2}\theta\). The appearance of \({A}_{2}\) term directly shows the original orthorhombic symmetry is broken at low temperature, which is consistent with polarity (P) along the out-of-plane b axis (P//b) in our nonlinear transport results (see Supplementary Fig. 4 and Supplementary Note 2 for details of symmetry analyses). We now show that the AHE is the direct consequence of this polar distortion. As shown in Fig. 2b, \({\sigma }_{{xy}}^{A}\) starts to show up and exhibits plateau-like structures beyond a critical magnetic field \({{{{{{\rm{B}}}}}}}_{p}\). As shown in Fig. 2c, we extract the temperature-dependent coefficients \({A}_{1}\), \({A}_{2}\), and \({\sigma }_{{xy}}^{A}\), and plot the ratios of \({A}_{{{{{\mathrm{1,2}}}}}}(T)/{A}_{{{{{\mathrm{1,2}}}}}}(270{K})\) and \({\sigma }_{{xy}}^{A}\) together. \({A}_{1}(T)/{A}_{1}(270{K})\) exhibits moderate temperature dependence and dominates over the total torque \({\tau }_{a}\) in the whole temperature range (see Supplementary Fig. 3a for the raw data). However, \({A}_{2}(T)\) is almost negligible at temperatures higher than 150 K, below which the ratio of \({A}_{2}(T)/{A}_{2}(270{K})\) suddenly gets enhanced and reaches a value of ~30 at 2 K, indicating the emergence of polar distortion at 150 K. Furthermore, as shown in Fig. 2c, \({\sigma }_{{xy}}^{A}\) shows up around 150 K, where the \({A}_{2}\) term suddenly gets enhanced. The concurrence of the polar distortion and \({\sigma }_{{xy}}^{A}\) indicates that the AHE is locked to the polar distortion-induced band modifications, which is also consistent with the fact that no AHE is observed in CVT samples20.
ZrTe5 is a nonmagnetic material with time-reversal symmetry. Nevertheless, the observed AHE takes a profile like the AHE of ferromagnets with saturating plateaus. Based on our three observations: 1. The existence of polar distortion P//b; 2. The coincidence of the onsets of the AHE and polar distortions; 3. The absence of the in-plane Hall effect in our samples (see Supplementary Fig. 5 and Supplementary Note 3 for the in-plane Hall discussions). Considering the quasi-2D nature of ZrTe5, we interpret this behavior by invoking a Rashba model-based mechanism usually adopted for explaining the intrinsic AHE in magnetic materials\(\lambda=\frac{2{\pi }^{2}{k}_{B}{m}_{c}}{\hslash {eB}}T\) of the Lifshitz–Kosevich (L–K) formula42, where \({k}_{B}\) is the Boltzmann constant (see Supplementary Fig. 9 for more details on the L–K formula fittings). As shown in Fig. 4c, the resulting cyclotron mass (\({m}_{c}\)) gets heavily enhanced (ratio ~102) in magnetic fields. The temperature-dam** prefactor \({\lambda }_{D}\) of the L–K formula for Dirac fermion43 is written as \({\lambda }_{D}=\frac{2{\pi }^{2}{k}_{B}\left|\mu \right|}{\hslash {eB}{v}_{F}^{2}}T\), where the \(\mu\) is the chemical potential. Then, the cyclotron mass \({m}_{c}\) fitted by \(\lambda\) effectively reflects the quantity \(\left|\mu \right|/{v}_{F}^{2}\) in the Dirac system, this is consistent with the universal definition \({m}_{c}=\frac{{\hslash }^{2}}{2\pi }\frac{\partial {A}_{k}}{\partial E}\), where \({A}_{k}\) is the extremal area of orbital. By using the fixed carrier density (p) constrain in real systems, we come to \({m}_{c}=\hslash {\left(6{\pi }^{2}p\right)}^{\frac{1}{3}}/{v}_{F}\), means enhanced \({m}_{c}\) corresponds to a reduction of \({v}_{F}\), supporting the formation of a topological flat band. Figure 4d shows the magnetic field dependence of \({v}_{F}\) (zero-field \({v}_{F}\) ~ 5\(\times\)105 m/s), and the lowest value of \({v}_{F}\) is around 103 m/s at ~20 T. These effects of cyclotron mass enhancement and \({v}_{F}\) reduction are similar to that in twisted bilayer graphene4, while much stronger than those observed in the NLSM44 and Kondo insulator\({\lambda }_{D}\) of the L–K formula.
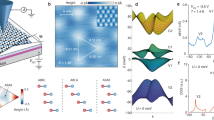
Let’s come to a picture based on the above experimental observations. As illustrated in Fig. 5a, the topmost Rashba-splitted band A flattens in a magnetic field, and the kinetic energy is heavily quenched. At the same time, the lower band is still dispersive with large kinetic energy and then goes up quickly in the magnetic field. The simplified band A, as a topological flat band, thus exhibits quenched kinetic energy and dominated Zeeman energy. Then, the Landau levels will bend and reappear to FL, which is essentially different from the normal quantum oscillations. The quantum limit defined in this picture is equal to that in normal quantum oscillations estimated by carrier concentration, namely the critical field where the LLL solely occupies (higher LLs will bend over and reappear later). We plot the kinetic energy \({E}_{{LL},{kinetic}}=-\scriptstyle\sqrt{2{nB}{v}_{x}{v}_{y}e\hslash }\) (Fig. 5b) with fitted \({m}_{c}\), which quenches at small fields. As shown in Fig. 5c, we plot the total energy \({E}_{n}=-\scriptstyle\sqrt{2{nB}{v}_{x}{v}_{y}e\hslash }+\frac{\bar{g}}{2}{\mu }_{B}B\) (\(\bar{g}\) ~15), and find the Landau levels cross the FL, distributing evenly in high magnetic fields. Therefore, the anomalous resistance oscillations observed beyond the quantum limit are consistent with forming a topological flat band in ZrTe5.
a Formation of Landau levels on the topological flat band with dominant Zeeman effect. b The kinetic energy, \({E}_{{LL},{kinetic}}=-\sqrt{2{nB}{v}_{x}{v}_{y}e\hslash }\), of Landau levels obtained from experimental cyclotron mass, showing the quenched kinetic energy at high fields. c The total energy of Landau levels, including the dominant Zeeman effect \(\frac{\bar{g}}{2}{\mu }_{B}B\), exhibiting the reappearance of Landau levels across the Fermi level (FL) denoted as a dashed pink line.