Introduction

In today’s highly competitive market, how and when to send the products to the customers becoming more challenging as they want in a cost effective manner. Transportation models provide a powerful framework to meet this challenge. The transportation problem was first developed by Hitchcock [1]. When different modes of transportation are available, then we must transport goods from sources to destinations by different ways in a cost effective manner and also within the time, for this solid transportation problem is suitable. Shell [2] first stated the solid transportation problem and Haley [3] developed a solution procedure of the solid transportation problem. Fuzzy linear programming technique was applied to multi objective solid transportation problem by Bit et al. [4]. As a result of this an efficient solution was obtained.

Type-2 fuzzy sets are proposed by Zadeh et al. [5] as the generalization of type-1 fuzzy sets. Type-2 fuzzy sets are described by both primary and secondary membership to provide more degrees of freedom and flexibility and they are three dimensional. Therefore type-2 fuzzy sets have the advantage of modelling uncertainty more accurately compared with type-1 fuzzy sets. However, when the type-2 fuzzy sets are employed to solve the problems, computational burden is heavy [6]. Hence interval type-2 fuzzy sets are extensively utilized with some relative representations such as vertical slice representation, wavy-slice representation to reduce dimensions, which are extremely useful for computation and theoretical studies [7]. Interval type-2 fuzzy sets can be viewed as a special case of general type-2 fuzzy sets that all the values of secondary membership are equal to 1. Hence it not only represents uncertainty better than type-1 fuzzy sets do, also reduces the computation compared to type-2 fuzzy sets. Mendel et al. [6] proposed some definitions of interval type-2 fuzzy sets. Mitchell [8] and Zeng and Li [9] designed method to calculate the similarity among interval type-2 fuzzy sets. To reduce limitations in these methods, Wu and Mendel [10] developed a new method named vector similarity method (VSM) to transform interval type-2 fuzzy sets into word more effectively. Ondrej and Milos [11] employed interval type-2 fuzzy sets to develop a fuzzy voter design for fault tolerant systems. Shu and Liang [12] proposed a new approach based on interval type-2 fuzzy logic systems to analyze and estimate the network lifetime for wireless sensor networks. Wu and Mendel [13] defined linguistic weighted average and employed it to deal with hierarchical multi- criteria decision making problems. Han and Mendel [14] employed interval type-2 fuzzy numbers in choosing logistic location and the result has been proved to be more satisfying. Chen and Lee [15] proposed the definition of possibility degree of trapezoidal interval type-2 fuzzy numbers and some arithmetic operations.

In-spite of rapid developments of transportation models there are still some gaps, these are summarize as follows,

  • Profit maximization with time minimization in a single mathematical formulation perhaps not available in literature as per our knowledge.

  • Solid transportation problems (STP) with interval type-2 fuzzy variables are also rare.

  • As per literature survey, use of an interactive method to solve a STP is not there.

All these important issues, that missed by the previous researchers lead us to investigate the present study by considering all the above mentioned lacunas.

In this paper, we have considered the uncertainties in the multi-objective solid transportation problems as fuzzy. Models in fuzzy environment, we consider unit transportation cost, time of transportation, unit selling price, unit cost price, demand and source capacity as trapezoidal interval type-2 fuzzy number and expected value technique is being applied to covert the fuzzy models in crisp environment. Later, Interactive fuzzy satisficing method has been applied to solve the designed problems also a numerical example has been given to demonstrate the models.

Preliminaries

Interval Type-2 Fuzzy Set

Definition 1

[6]: Let \(\tilde{A}\) be a type-2 fuzzy set, then \(\tilde{A}\) can be expressed as \(\tilde{A} =\left\{ {\left( {\left( {x,u} \right) \!, \mu _{\tilde{A}} \left( {x,u} \right) } \right) \vert \forall x\in X,\forall u\in J_x \subseteq \left[ {0,1} \right] ,0\le \mu _{\tilde{A}} \left( {x,u} \right) \le 1} \right\} \), where \(X\) is the universe of discourse and \(\mu _{\tilde{A}}\) denotes the membership function of \(\tilde{A}\). \(\tilde{A}\) can be expressed as \(\tilde{A} = \int _{x\in X} \int _{u\in J_x } \mu _{\tilde{A}} \left( {x,u} \right) /(x,u), u\in J_x \subseteq [0,1]\).

Definition 2

[6]: For a type-2 fuzzy set \(\tilde{A}\), if all \(\mu _{\tilde{A}} \left( {x,u} \right) =1\) then \(\tilde{A}\) is called an interval type-2 fuzzy set, i.e., \(\tilde{A} = \int _{x\in X} \int _{u\in J_x } 1/(x,u), u\in J_x \subseteq [0,1]\).

Definition 3

[6]: Uncertainty in the primary memberships of a type-2 fuzzy set, \(\tilde{A}\) consists of a bounded region that we call the footprint of uncertainty \((FOU)\). It is the union of all primary memberships i.e., \(FOU(\tilde{A})= {\cup }_{x\in X} J_x\).

\(FOU\) is characterized by the upper membership function \((UMF)\) and the lower membership function \((LMF)\), and are denoted by \(\bar{\mu }_{\tilde{A}}\) and \(\underline{\mu }_{\tilde{A}}\).

Definition 4

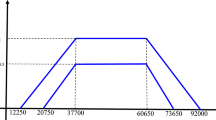
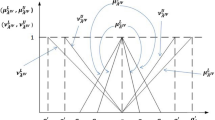
[15]: An interval type-2 fuzzy number is called a trapezoidal interval type-2 fuzzy number where the \(UMF\) and \(LMF\) are both trapezoidal fuzzy numbers, i.e.,

$$\begin{aligned} A=( {A^{U},A^{L}} )= & {} \left( \left( {a_1^U ,a_2^U ,a_3^U ,a_4^U ; H_1 ( {A^{U}} ),H_2 ( {A^{U}} )} \right) \!, \right. \nonumber \\&\quad \left. \left( {a_1^L ,a_2^L ,a_3^L ,a_4^L ; H_1 ( {A^{L}} ),H_2 ( {A^{L}} )} \right) \right) \end{aligned}$$
(1)

where \(H_j ( {A^{L}} )\) and \(H_j ( {A^{U}} )(j=1,2)\) denote membership values of the corresponding elements \(a_{j+1}^L\) and \(a_{j+1}^U\) respectively. Figure 1 gives the pictorial representation of an trapezoidal interval type-2 fuzzy number.

Defuzzification of Trapezoidal Interval Type-2 Fuzzy Number [16]

Let us consider a trapezoidal interval type-2 fuzzy number \(A\), given by Eq. (1). The expected value of \(A\) is defined as follows:

$$\begin{aligned} E\left( A \right) = \frac{1}{2}\left( {\frac{1}{4}\mathop {\sum }\limits _{i=1}^4 ( {a_i^L +a_i^U } )} \right) \times \frac{1}{4}\left( {\mathop {\sum }\limits _{i=1}^2 \left( {H_i ( {A^{L}} )+ H_i ( {A^{U}} )} \right) } \right) \end{aligned}$$
(2)

Assuming that \(A_1\) and \(A_2\) are two trapezoidal interval type-2 fuzzy numbers, then we have \(A_1 >A_2\) if and only if \(E(A_1 )>E( {A_2 } )\).

When \(a_i^L =a_i^U ( {i=1,2,3,4} )\) and \(H_1 ( {A^{L}} )=H_2 ( {A^{L}} )=H_1 ( {A^{U}} )=H_1 ( {A^{U}} )\), the trapezoidal interval type-2 fuzzy number reduces to trapezoidal fuzzy number, just as \(\acute{A} =( {a_1^L ,a_2^L ,a_3^L ,a_4^L } )\). The expected value of \(\acute{A}\) is \(E( {\acute{A} })=\left( {a_1^L +a_2^L +a_3^L +a_4^L } \right) /4\).

Fig. 1
figure 1

Trapezoidal Interval Type-2 Fuzzy Number

Full size image

The Arithmetic Operations of Interval Type-2 Fuzzy Set [15]

Suppose \(A_1\) and \(A_2\) are two trapezoidal interval type-2 fuzzy numbers:

$$\begin{aligned} A_1 =\left( {A_1^U ,A_1^L } \right)= & {} \left( \left( {a_{11}^U ,a_{12}^U ,a_{13}^U,a_{14}^U ;H_1 \left( {A_1^U } \right) \!, H_2 \left( {A_1^U } \right) } \right) \!, \right. \nonumber \\&\quad \left. \left( {a_{11}^L ,a_{12}^L ,a_{13}^L,a_{14}^L ;H_1 \left( {A_1^L } \right) \!, H_2 \left( {A_1^L } \right) } \right) \right) \end{aligned}$$
(3)
$$\begin{aligned} A_2 =\left( {A_2^U ,A_2^L } \right)= & {} \left( \left( {a_{21}^U ,a_{22}^U,a_{23}^U ,a_{24}^U ;H_1 \left( {A_2^U } \right) \!, H_2 \left( {A_2^U } \right) } \right) \!, \right. \nonumber \\&\quad \left. \left( {a_{21}^L ,a_{22}^L ,a_{23}^L,a_{24}^L ;H_1 \left( {A_2^L } \right) \!, H_2 \left( {A_2^L } \right) } \right) \right) \end{aligned}$$
(4)
$$\begin{aligned}&(1)\quad A_1 +A_2 =\left( {A_1^U ,A_1^L } \right) +\left( {A_2^U ,A_2^L } \right) \\&\qquad \quad =\left( {{ \begin{array}{l} \left( a_{11}^U +a_{21}^U,a_{12}^U +a_{22}^U,a_{13}^U +a_{23}^U,a_{14}^U +a_{24}^U ;\min \left( H_1 \left( A_1^U \right) \!, H_1 \left( A_2^U \right) \right) \right. ,\\ \quad \left. {\min \left( H_2 \left( {A_1^U } \right) \!, H_2 \left( {A_2^U } \right) \right) }\right) , \\ \left( a_{11}^L +a_{21}^L,a_{12}^L +a_{22}^L,a_{13}^L +a_{23}^L,a_{14}^L +a_{24}^L ;\min \left( {H_1 \left( {A_1^L } \right) , H_1 \left( {A_2^L } \right) }\right) \right. ,\\ \quad \left. {\min \left( H_2 \left( A_1^L \right) \!, H_2 \left( A_2^L \right) \right) }\right) \\ \end{array} }} \right) .\\&(2)\quad A_1 -A_2 =\left( {A_1^U,A_1^L } \right) -\left( {A_2^U,A_2^L} \right) \\&\qquad \quad =\left( {{\begin{array}{l} {\left( {a_{11}^U -a_{21}^U,a_{12}^U -a_{22}^U,a_{13}^U -a_{23}^U,a_{14}^U -a_{24}^U;}\right. }\\ \quad {\left. {\min \left( {H_1 \left( {A_1^U } \right) ,H_1 \left( {A_2^U } \right) } \right) \!, \min \left( {H_2 \left( {A_1^U } \right) \!, H_2 \left( {A_2^U } \right) } \right) } \right) ,} \\ {\left( {a_{11}^L -a_{21}^L,a_{12}^L -a_{22}^L,a_{13}^L -a_{23}^L,a_{14}^L -a_{24}^L;}\right. }\\ \quad {\left. {\min \left( {H_1 \left( {A_1^L } \right) ,H_1 \left( {A_2^L} \right) } \right) ,\min \left( {H_2 \left( {A_1^L } \right) \!, H_2 \left( {A_2^L } \right) } \right) } \right) } \\ \end{array} }} \right) .\\&(3)\quad A_1 \times A_2 =\left( {A_1^U,A_1^L} \right) \times \left( {A_2^U,A_2^L } \right) \\&\qquad \quad =\left( {{\begin{array}{l} {\left( {a_{11}^U \times a_{21}^U,a_{12}^U \times a_{22}^U,a_{13}^U \times a_{23}^U,a_{14}^U \times a_{24}^U ;}\right. }\\ \quad {\left. {\min \left( {H_1 \left( {A_1^U } \right) , H_1 \left( {A_2^U } \right) } \right) ,\min \left( {H_2 \left( {A_1^U } \right) , H_2 \left( {A_2^U } \right) } \right) } \right) ,} \\ {\left( {a_{11}^L \times a_{21}^L,a_{12}^L \times a_{22}^L,a_{13}^L \times a_{23}^L,a_{14}^L \times a_{24}^L ;}\right. }\\ \quad {\left. {\min \left( {H_1 \left( {A_1^L } \right) \!, H_1 \left( {A_2^L } \right) } \right) \!, \min \left( {H_2 \left( {A_1^L } \right) ,H_2 \left( {A_2^L } \right) } \right) } \right) } \\ \end{array} }} \right) .\\&(4)\quad kA_1 =\left( { \left( {ka_{11}^U,ka_{12}^U,ka_{13}^U,ka_{14}^U;H_1 \left( {A_2^U } \right) , H_2 \left( {A_2^U } \right) } \right) }\right. ,\\&\qquad \qquad \qquad \quad \quad \left. {\left( {ka_{11}^L,ka_{12}^L,ka_{13}^L,ka_{14}^L;H_1 \left( {A_2^L } \right) ,H_2 \left( {A_2^L } \right) } \right) } \right) .\\&(5)\quad \frac{1}{k}A_1 =\left( { \left( {\frac{1}{k}a_{11}^U,\frac{1}{k}a_{12}^U,\frac{1}{k}a_{13}^U,\frac{1}{k}a_{14}^U;H_1 \left( {A_1^U} \right) ,H_2 \left( {A_1^U } \right) } \right) }\right. ,\\&\qquad \qquad \quad \quad \quad \left. {\left( {\frac{1}{k}a_{11}^L,\frac{1}{k}a_{12}^L,\frac{1}{k}a_{13}^L,\frac{1}{k}a_{14}^L ;H_1 \left( {A_1^L } \right) ,H_2 \left( {A_1^L } \right) } \right) } \right) . \end{aligned}$$

Several drawbacks are found in the above arithmetic operations as shown below:

In addition and subtraction it is unreasonable to pick up the minimum membership of upper and lower membership function respectively, because it ignores the influence of larger membership function

Example 1

Let \(A_1 = ( ( {1,5,8,12;0.7,0.8} )\), \(( {3,5,7,10;0.5,0.6} ) )\) and \(A_2 =( ( 2,5,7,8;0.6,0.7 )\), \(( {3,4,6,7;0.3,0.5} ) )\), then we can get,

$$\begin{aligned} A_1 +A_2= & {} \left( {\left( {3,10,15,20;0.6,0.7} \right) \!, \left( {6,9,13,17;0.3,0.5} \right) } \right) .\\ A_1 -A_2= & {} \left( {\left( {-1,0,1,4;0.6,0.7} \right) \!, \left( {0,1,1,0;0.3,0.5} \right) } \right) . \end{aligned}$$

In this way, the impact of the second trapezoidal interval fuzzy number’s membership has been neglected.

The reciprocal influence of different trapezoidal interval type-2 fuzzy number is not taken into consideration in the multiplication operation, and the outcome prove to be true only when all the elements of \(UMF\) and \(LMF\) are larger than zero.

Example 2

Le \(A_1 =( ( {-4,-3,1,3;0.7,0.7} )\), \(( {-3,-2,1,2;0.6,0.5} ) )\) and \(A_2 =( ( -3,-2,0,1;0.5,0.8 )\), \(( {-2,-1,-1,0;0.4,0.6} ) )\) be two trapezoidal interval type-2 fuzzy numbers, based on the given operation, it can be computed that

$$\begin{aligned} A_1 \times A_2 =\left( {\left( {12,6,0,3,0.5,0.7} \right) \!, \left( {6,2,-1,0,0.4,0.5} \right) } \right) . \end{aligned}$$

Obviously, the outcome is wrong.

The effect of value on the membership value of the element is ignored.

Example 3

Let \(A_1 =\big ( {( {1,2,3,4;0.5,0.8} ),( {2,3,4,6;0.4,0.5} )} \big )\) then \(2A_1 =\big ( ( 2,4,6,8;\) \(0.5,0.8 ), ( {4,6,8,12;0.4,0.5} ) \big )\)

To address the drawbacks mentioned above, the improved arithmetic operations are defined as follows:

Let us consider two trapezoidal interval type-2 fuzzy numbers \(A_1\) and \(A_2\) given by Eqs. (3) and (4). Then,

$$\begin{aligned}&1) \quad A_1 +A_2 =\left( {A_1^U ,A_1^L } \right) +\left( {A_2^U ,A_2^L } \right) =\left( \left( a_{11}^U +a_{21}^U ,a_{12}^U +a_{22}^U ,a_{13}^U +a_{23}^U ,a_{14}^U +a_{24}^U ;\right. \right. \\&\qquad \left. H_1 \left( {A_1^U } \right) +H_1 \left( {A_2^U } \right) -H_1 \left( {A_1^U } \right) \cdot H_1 \left( {A_2^U } \right) \!, H_2 \left( {A_1^U } \right) +H_2 \left( {A_2^U } \right) \right. \\&\qquad \left. -H_{2} \left( {A_1^U } \right) \cdot H_2 \left( {A_2^U } \right) \right) \!, \left( a_{11}^L +a_{21}^L ,a_{12}^L +a_{22}^L ,a_{13}^L +a_{23}^L ,a_{14}^L +a_{24}^L ; H_1 \left( {A_1^L } \right) \right. \\&\qquad \left. \left. +H_1 \left( {A_2^L } \right) -H_1 \left( {A_1^L } \right) \cdot H_1 \left( {A_2^L } \right) \!, H_{2} \left( {A_1^L } \right) +H_{2} \left( {A_2^L } \right) -H_{2} \left( {A_1^L } \right) \cdot H_{2} \left( {A_2^L } \right) \right) \right) .\\&2)\quad A_1 -A_2 =\left( \left( a_{11}^U -a_{24}^U ,a_{12}^U -a_{23}^U ,a_{13}^U -a_{22}^U ,a_{14}^U -a_{21}^U ;H_1 \left( {A_1^U } \right) +H_1 \left( {A_2^U } \right) \right. \right. \\&\qquad \left. -H_1 \left( {A_1^U } \right) \cdot H_1 \left( {A_2^U } \right) \!, H_2 \left( {A_1^U } \right) +H_2 \left( {A_2^U } \right) -H_2 \left( {A_1^U } \right) \cdot H_2 \left( {A_2^U } \right) \right) \!, \\&\qquad \left( a_{11}^L -a_{24}^L ,a_{12}^L -a_{23}^L ,a_{13}^L -a_{22}^L ,a_{14}^L -a_{21}^L ; H_1 \left( {A_1^L } \right) +H_1 \left( {A_2^L } \right) \right. \\&\qquad \left. \left. -H_1 \left( {A_1^L } \right) \cdot H_1 \left( {A_2^L } \right) \!, H_2 \left( {A_1^L } \right) +H_2 \left( {A_2^L } \right) -H_2 \left( {A_1^L } \right) \cdot H_2 \left( {A_2^L } \right) \right) \right) .\\&3)\quad A_1 \times A_2 =\left( {A_1^U ,A_1^L } \right) \times \left( {A_2^U ,A_2^L } \right) \\&\qquad =\left( {{\begin{array}{l} {\left( {x_{11}^U ,x_{12}^U ,x_{13}^U ,x_{14}^U ;H_1 \left( {A_1^U } \right) \cdot H_1 \left( {A_2^U } \right) \!, H_2 \left( {A_1^U } \right) \cdot H_2 \left( {A_2^U } \right) } \right) \!,} \\ {\left( {x_{11}^L ,x_{12}^L ,x_{13}^L ,x_{14}^L ;H_1 \left( {A_1^L } \right) \cdot H_1 \left( {A_2^L } \right) \!, H_2 \left( {A_1^L } \right) \cdot H_2 \left( {A_2^L } \right) } \right) } \\ \end{array} }} \right) . \end{aligned}$$

where \(x_{1i}^T =\min \left( {a_{1i}^T a_{2i}^T , a_{1i}^T a_{2\left( {5-i} \right) }^T , a_{1\left( {5-i} \right) }^T a_{2i}^T , a_{1\left( {5-i} \right) }^T a_{2\left( {5-i} \right) }^T } \right) \!, T\in \left\{ {U,L} \right\} , i\in \left\{ {1, 2} \right\} \) and \(x_{1j}^T =\hbox {max}\,\left( {a_{1\left( {5-j} \right) }^T a_{2\left( {5-j} \right) }^T , a_{1\left( {5-j} \right) }^T a_{2j}^T ,a_{1j}^T a_{2\left( {5-j} \right) }^T , a_{1j}^T a_{2j}^T } \right) \!, T\in \left\{ {U,L} \right\} , i\in \{3,4\}\).

$$\begin{aligned}&4)\quad {\lambda } A_1 =\left( {{\begin{array}{l} {\left( {{\lambda }a_{11}^U ,{\lambda }a_{12}^U ,{\lambda }a_{13}^U ,{\lambda }a_{14}^U ;1-\left( {1-H_1 \left( {A_1^U } \right) } \right) ^{\lambda },1-\left( {H_2 \left( {A_1^U } \right) } \right) ^{\lambda }} \right) \!,} \\ {\left( {{\lambda }a_{11}^L ,{\lambda }a_{12}^L ,{\lambda }a_{13}^L ,{\lambda }a_{14}^L ;1-\left( {1-H_1 \left( {A_1^L } \right) } \right) ^{\lambda },1-\left( {H_2 \left( {A_1^L } \right) } \right) ^{\lambda }} \right) } \\ \end{array} }} \right) .\\&3)\quad A_1^{\lambda } =\left( {{\begin{array}{l} {\left( {a_{11}^U } \right) ^{\lambda },\left( {a_{12}^U } \right) ^{\lambda },\left( {a_{13}^U } \right) ^{\lambda },\left( {a_{14}^U } \right) ^{\lambda };\left( {H_1 \left( {A_1^U } \right) } \right) ^{\lambda },\left( {H_2 \left( {A_1^U } \right) }\right) ^{\lambda },} \\ {\left( {\left( {a_{11}^L } \right) ^{\lambda },\left( {a_{12}^L } \right) ^{\lambda },\left( {a_{13}^L } \right) ^{\lambda };\left( {H_1 \left( {A_1^L } \right) } \right) ^{\lambda },\left( {H_2 \left( {A_1^L } \right) }\right) ^{\lambda }}\right) } \\ \end{array} }} \right) . \end{aligned}$$

Interactive Fuzzy Satisficing Method [17, 18]

Step-1: Each individual objective function \(f_i (x)\) under the given constraints is considered and its minimum value \(f_i^{min}\) and maximum value \(f_i^{max}\) for \(i=1,2,\ldots .k\) are determined.

Step-2: Depending upon these maximum and minimum values, Decision maker (DM) specifies lower limit \(L_i\) and upper limit \(U_i\) of \(\mu _{f_i } (x)\) where \(f_i^{min} \le L_i \le U_i \le f_i^{max}\) for \(i=1,2,\ldots ,k\).

Step-3: DM constructs membership function \(\mu _{f_i } \left( x \right) \) for each of the objective functions \(f_i (x)\) as in case (a) and in case (b).

  • Case (a): Membership function \(\mu _{f_i} (x)\) for minimization type objective function is:

    $$\begin{aligned} \mu _{f_i } \left( x \right) =\left\{ {{\begin{array}{ll} 1 &{} \textit{for}\,L_i <f_i (x) \\ 1-\frac{f_i \left( x \right) -L_i }{U_i -L_i } &{} \textit{for}\,L_i \le f_i (x)\le U_i \\ 0 &{} \textit{for}\,f_i (x)>U_i \\ \end{array} }} \right. \end{aligned}$$
    (5)

  • Case (b): Membership function \(\mu _{f_i } (x)\) for maximization type objective function is:

    $$\begin{aligned} \mu _{f_i } \left( x \right) =\left\{ {{\begin{array}{ll} 0 &{} \textit{for}\,f_i (x)<L_i \\ 1-\frac{U_i -f_i \left( x \right) }{U_i -L_i} &{} \textit{for}\,L_i \le f_i (x)\le U_i \\ 1 &{} \textit{for}\,f_i (x)>U_i \\ \end{array} }} \right. \end{aligned}$$
    (6)

Step-(3): solve the following problem.

$$\begin{aligned} \left. { {\begin{array}{l} Minimize \,v \\ subject\,to, \bar{\mu }_i -\mu _{f_i } \left( x \right) \le v, \\ \forall \,i=1,2,\ldots , k\,\hbox {and}\,x\in X \\ \end{array} }} \right\} \end{aligned}$$
(7)

where decision maker updates reference membership levels \(\bar{\mu }_i\), \(\forall i=1,2,\ldots , k\) through interaction.

Step-(4): It should be noted that if an optimal solution \(x^{*}\) to the problem in step-(3) is unique then \(x^{*}\) is an M-Pareto optimal solution. The uniqueness of \(x^{*}\) can be tested by solving the M-Pareto optimality test problem (below)

$$\begin{aligned} \left. {{\begin{array}{l} Maximize \mathop {\sum }\limits _{i=1}^{k}\upvarepsilon _{i} \\ subject\,to, \mu _{f_i } \left( x \right) -\upvarepsilon _i =\mu _{f_i } \left( {x^{*}} \right) \!, \\ x\in X, \quad \bar{\upvarepsilon } =\left( {{\upvarepsilon }_2 ,{\upvarepsilon }_2 ,\ldots .{\upvarepsilon }_k } \right) ^{\mathrm{T}}\ge 0 \\ \end{array} }} \right\} \end{aligned}$$
(8)

For the optimal solution \(\bar{x} , \bar{\upvarepsilon }\) to problem on step-(4):

  1. (i)

    If \(\bar{\upvarepsilon } =0\) then \(x^{*}\) is an M-Pareto optimal solution of the problem defined in step-3.

  2. (ii)

    If \(\bar{\upvarepsilon } \ne 0\) then not \(x^{*}\) but \(\bar{x}\) is an M-Pareto optimal solution of the problem defined in step-4.

M-Pareto optimal solution: \(x^{*}\in X\) is said to be an M-Pareto optimal solution if and only if there does not exist another \(x\in X\) such that \(\mu _i \left( {z_i \left( x \right) } \right) \ge \mu _i \left( {z_i \left( {x^{*}} \right) } \right) \) for all \(i\) and \(\mu _j \left( {z_j \left( x \right) } \right) \ge \mu _j \left( {z_j \left( {x^{*}} \right) } \right) \) at least one \(j\).

Model Formulation and Crisp Equivalences of the Models

The following notations and assumptions are used throughout the model.

Notations

  • \(M\): Number of plants of the transportation problem.

  • \(N\): Number of destinations of the transportation problem.

  • \(K\): Number of conveyances of the transportation problem.

  • \(\tilde{c}_{ijk}\): Fuzzy unit transport cost to transport the commodity from \(i^\mathrm{th}\) plant to \(j^\mathrm{th}\) destination by \(k^\mathrm{th}\) conveyance.

  • \(\tilde{t}_{ijk}\): Transportation time to transport the commodity from \(i^\mathrm{th}\) plant to \(j^\mathrm{th}\) destination by \(k^\mathrm{th}\) conveyance.

  • \(x_{ijk}\): Unknown quantity which is to transport the commodity from \(i^\mathrm{th}\) plant to \(j^\mathrm{th}\) destination by \(k^\mathrm{th}\) conveyance (decision variable).

  • \(\tilde{a}_i\): Fuzzy amount of homogenous product available at the \(i^\mathrm{th}\) plant.

  • \(\tilde{b}_j\): Fuzzy demand at the \(j^\mathrm{th}\) destination.

  • \(\tilde{e}_k\): Fuzzy amount of product which can be carried by the \(k^\mathrm{th}\) conveyance.

  • \(\tilde{s}_j\): The fuzzy selling price at \(j^\mathrm{th}\) destination.

  • \(\tilde{p}_i\): The fuzzy purchase cost at \(i^\mathrm{th}\) plant.

  • \(s_j\): The crisp selling price at \(j^\mathrm{th}\) destination.

  • \(p_i\): The crisp purchase cost at \(i^\mathrm{th}\) source.

  • \(b_j\): Crisp demand at the \(j^\mathrm{th}\) destination.

  • \(a_i\): Crisp amount of homogenous product available at the \(i^\mathrm{th}\) source.

  • \(e_k\): Crisp amount of product which can be carried by the \(k^\mathrm{th}\) conveyance.

Assumptions

  • The models are unbalanced problems.

  • If the unknown quantity which is to be transported from \(i^\mathrm{th}\) source to \(j^\mathrm{th}\) destination by different mode of \(k^\mathrm{th}\) conveyances is \(x_{ijk} >0\) then for the convenience of medelling we define \(y_{ijk}\) as follows:

    $$\begin{aligned} y_{ijk} =\left\{ {{\begin{array}{ll} 1 &{} \textit{for} \, x_{ijk} >0 \\ 0 &{} otherwise \\ \end{array} }} \right. \end{aligned}$$

Model-I: Selling Price, Purchase Cost, Unit Transportation Cost, Time are Trapezoidal Interval Type-2 Fuzzy Numbers and Source, Demands and Conveyance Capacities are Crisp

$$\begin{aligned}&\hbox {Max}\,f_1 =\mathop {\sum }\limits _{i=1}^M \mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K \left( {\tilde{s}_j -\tilde{p}_i -\tilde{c}_{ijk} } \right) x_{ijk} \end{aligned}$$
(9)
$$\begin{aligned}&\hbox {Min}\,f_2 =\mathop {\sum }\limits _{i=1}^M \mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K \tilde{t}_{ijk} y_{ijk} \end{aligned}$$
(10)
$$\begin{aligned}&subject\,to,\nonumber \\&\mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K x_{ijk} \le a_i \end{aligned}$$
(11)
$$\begin{aligned}&\mathop {\sum }\limits _{i=1}^M \mathop {\sum }\limits _{k=1}^K x_{ijk} \ge b_j \end{aligned}$$
(12)
$$\begin{aligned}&\mathop {\sum }\limits _{i=1}^M \mathop {\sum }\limits _{j=1}^N x_{ijk} \le e_k \end{aligned}$$
(13)
$$\begin{aligned}&x_{ijk} \ge 0,\forall i,j,k \end{aligned}$$
(14)

Crisp Transformation of the Fuzzy Model-I

In model-1, selling price, purchase cost, unit transportation cost and time are trapezoidal interval type-2 fuzzy numbers. To convert the interval type-2 fuzzy numbers into its equivalent crisp number by finding the expectations. Therefore the type-2 fuzzy model-1 converted to its crisp model in the following way.

The first objective function i.e., profit maximizing objective function given by Eq. (9) in model-I become,

$$\begin{aligned}&\hbox {Max}\,f_1 =\mathop {\sum }\limits _{i=1}^M \mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K \left( {\tilde{s}_j -\tilde{p}_i -\tilde{c}_{ijk} } \right) x_{ijk}\\&\quad = \mathop {\sum }\limits _{i=1}^M \mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K \left( {\left( {s_j^U ,s_j^L } \right) -\left( {p_i^U ,p_i^L } \right) -\left( {c_{ijk}^U ,c_{ijk}^L } \right) } \right) x_{ijk}\\&\quad =\mathop {\sum }\limits _{i=1}^M \mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K \left( {{\begin{array}{l} \left( {\left( {s_{j1}^U ,s_{j2}^U ,s_{j3}^U ,s_{j4}^U ;H_1 \left( {s_j^U } \right) \!, H_2 \left( {s_j^U } \right) } \right) }\right. ,\\ \quad \left. {\left( {s_{j1}^L ,s_{j2}^L ,s_{j3}^L ,s_{j4}^L ;H_1 \left( {s_j^L } \right) \!, H_2 \left( {s_j^L } \right) } \right) } \right) - \\ \left( {\left( {p_{i1}^U ,p_{i2}^U ,p_{i3}^U ,p_{i4}^U ;H_1 \left( {p_i^U } \right) \!, H_2 \left( {p_i^U } \right) } \right) }\right. ,\\ \quad \left. {\left( {p_{i1}^L ,p_{i2}^L ,p_{i3}^L ,p_{i4}^L ;H_1 \left( {p_i^L } \right) \!, H_2 \left( {p_i^L } \right) } \right) } \right) - \\ \left( {\left( {c_{ijk1}^U ,c_{ijk2}^U ,c_{ijk3}^U ,c_{ijk4}^U ;H_1 \left( {c_{ijk}^U } \right) \!, H_2 \left( {c_{ijk}^U } \right) } \right) }\right. , \\ \quad \left. {\left( {c_{ijk1}^L ,c_{ijk2}^L ,c_{ijk3}^L ,c_{ijk4}^L ;H_1 \left( {c_{ijk}^L } \right) \!, H_2 \left( {c_{ijk}^L } \right) } \right) } \right) \\ \end{array} }} \right) x_{ijk}\\&\quad = \mathop {\sum }\limits _{{i = 1}}^{M} \mathop {\sum }\limits _{{j = 1}}^{N} \mathop {\sum }\limits _{{k = 1}}^{K} \frac{1}{8} \left( {\left( {s_{{j1}}^{U} - p_{{i4}}^{U} - c_{{ijk4}}^{U} } \right) + \left( {s_{{j2}}^{U} - p_{{i3}}^{U} - c_{{ijk3}}^{U} } \right) }\right. + \left( {s_{{j3}}^{U} - p_{{i2}}^{U} - c_{{ijk2}}^{U} } \right) \\&\qquad \left. {+ \left( {s_{{j4}}^{U} - p_{{i1}}^{U} - c_{{ijk1}}^{U} } \right) + \left( {s_{{j1}}^{L} - p_{{i4}}^{L} - c_{{ijk4}}^{L} } \right) + \left( {s_{{j2}}^{L} - p_{{i3}}^{L} - c_{{ijk3}}^{L} } \right) } \right. \\&\qquad \left. { + \left( {s_{{j3}}^{L} - p_{{i2}}^{L} - c_{{ijk2}}^{L} } \right) + \left( {s_{{j4}}^{L} - p_{{i1}}^{L} - c_{{ijk1}}^{L} } \right) } \right) \\&\qquad \times \frac{1}{4} \left( {\begin{array}{l} \left( {\left( {H_{1}\left( {s_{j}^{U} } \right) + H_{1} \left( {p_{i}^{U} } \right) - H_{1} \left( {s_{j}^{U} } \right) H_{1} \left( {p_{i}^{U} } \right) } \right) + H_{1} \left( {c_{{ijk}}^{U} } \right) }\right. \\ \quad \left. {- \left( {H_{1}\left( {s_{j}^{U} } \right) + H_{1} \left( {p_{i}^{U} } \right) - H_{1} \left( {s_{j}^{U} } \right) H_{1} \left( {p_{i}^{U} } \right) } \right) H_{1} \left( {c_{{ijk}}^{U} } \right) } \right) \\ + \left( {\left( {H_{2} \left( {s_{j}^{U} } \right) + H_{2} \left( {p_{i}^{U} } \right) - H_{2} \left( {s_{j}^{U} } \right) H_{2} \left( {p_{i}^{U} } \right) } \right) + H_{2} \left( {c_{{ijk}}^{U} } \right) }\right. \\ \quad \left. {- \left( {H_{2} \left( {s_{j}^{U} } \right) + H_{2} \left( {p_{i}^{U} } \right) - H_{2} \left( {s_{j}^{U} } \right) H_{2} \left( {p_{i}^{U} } \right) } \right) H_{2} \left( {c_{{ijk}}^{U} } \right) }\right) \\ + \left( {\left( {H_{1} \left( {s_{j}^{L} } \right) + H_{1} \left( {p_{i}^{L} } \right) - H_{1} \left( {s_{j}^{L} } \right) H_{1} \left( {p_{i}^{L} } \right) } \right) + H_{1} \left( {c_{{ijk}}^{L} } \right) }\right. \\ \quad \left. {- \left( {H_{1} \left( {s_{j}^{L} } \right) + H_{1} \left( {p_{i}^{L} } \right) - H_{1} \left( {s_{j}^{L} } \right) H_{1} \left( {p_{i}^{L} } \right) } \right) H_{1} \left( {c_{{ijk}}^{L} } \right) }\right) \\ + \left( {\left( {H_{2} \left( {s_{j}^{L} } \right) + H_{2} \left( {p_{i}^{L} } \right) - H_{2} \left( {s_{j}^{L} } \right) H_{2} \left( {p_{i}^{L} } \right) } \right) + H_{2} \left( {c_{{ijk}}^{L} } \right) }\right. \\ \quad \left. {- \left( {H_{2} \left( {s_{j}^{L} } \right) + H_{2} \left( {p_{i}^{L} } \right) - H_{2} \left( {s_{j}^{L} } \right) H_{2} \left( {p_{i}^{L} } \right) } \right) H_{2} \left( {c_{{ijk}}^{L} } \right) } \right) \\ \end{array} } \right) \end{aligned}$$

And the second objective function of model-I given by Eq. (10), which minimize the total transportation time transforms as,

$$\begin{aligned} \hbox {Min}\,f_2= & {} \mathop {\sum }\limits _{i=1}^M \mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K \tilde{t}_{ijk} y_{ijk} =\mathop {\sum }\limits _{i=1}^M \mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K \left( {t_{ijk}^U,t_{ijk}^L }\right) y_{ijk}\\= & {} \mathop {\sum }\limits _{i=1}^M \mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K \left( \left( {t_{ijk1}^U ,t_{ijk2}^U ,t_{ijk3}^U ,t_{ijk4}^U ;H_1 \left( {t_{ijk}^U } \right) \!, H_2 \left( {t_{ijk}^U } \right) } \right. , \right. \\&\quad \left. \left( {t_{ijk1}^L ,t_{ijk2}^L ,t_{ijk3}^L ,t_{ijk4}^L ;H_1 \left( {t_{ijk}^L } \right) \!, H_2 \left( {t_{ijk}^L } \right) } \right) \right) y_{ijk}\\= & {} \mathop {\sum }\limits _{i=1}^M \mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K \left( \frac{1}{8}\left( {t_{ijk1}^U +t_{ijk2}^U +t_{ijk3}^U +t_{ijk4}^U +t_{ijk1}^L +t_{ijk2}^L +t_{ijk3}^L +t_{ijk4}^L } \right) \right. \\&\times \left. \frac{1}{4}\left( {H_1 \left( {t_{ijk}^U } \right) +H_2 \left( {t_{ijk}^U } \right) +H_1 \left( {t_{ijk}^L } \right) +H_2 \left( {t_{ijk}^L } \right) } \right) \right) y_{ijk} \end{aligned}$$

Model-II: Selling Price, Purchase Cost, Unit Transportation Cost, Time, Source, Demands and Conveyance Capacities are Trapezoidal Interval Type-2 Fuzzy Numbers

We formulate a MOSTP with \(M\) plants, \(N\) customers and \(K\) conveyances and all suplies, demands, conveyances capacities, unit transportation cost, unit purchase cost, unit selling price, time at each customer as trapezoidal interval type-2 fuzzy number as follows:

$$\begin{aligned}&\hbox {Max}\,f_1 =\mathop {\sum }\limits _{i=1}^M \mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K \left( {\tilde{s}_j -\tilde{p}_i -\tilde{c}_{ijk} } \right) x_{ijk} \end{aligned}$$
(15)
$$\begin{aligned}&\hbox {Min}\,f_2 =\mathop {\sum }\limits _{i=1}^M \mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K \tilde{t}_{ijk} y_{ijk} \end{aligned}$$
(16)

subject to the constraints Eqs. (11)–(14) where \(a_i , b_j\) and \(e_k\) are fuzzy in nature for all \(i,j,k\).

Crisp Transformation of the Fuzzy Model-II

In model-2, all the parameters are trapezoidal interval type-2 fuzzy numbers. To convert the interval type-2 fuzzy numbers into its equivalent crisp number by finding the expectations. Therefore the type-2 fuzzy model -1 converted to its crisp model in the following way.

In model-II, both the objective functions Eqs. (15) and (16) are same as in model-I given by Eqs. (9) and (10). Therefor the crisp conversions for these two objective functions are same as of model-I (c.f. “Crisp Transformation of the Fuzzy Model-I” section).

And the fuzzy based inequality constraints are reduced as follows:

$$\begin{aligned} \mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K x_{ijk} \le \tilde{a}_i \end{aligned}$$
(17)

Now using Eq. (2) i.e., taking expectation on both side of Eq. (17) we get,

$$\begin{aligned}&E\left( {\mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K x_{ijk} } \right) \le E\left( {\tilde{a}_i } \right) \end{aligned}$$
(18)
$$\begin{aligned}&\Rightarrow \mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K x_{ijk} . E\left( 1 \right) \le E\left( {\tilde{a}_i} \right) \end{aligned}$$
(19)

since \(E\left( 1 \right) =1\), therefore the Eq. (19) become,

$$\begin{aligned}&\Rightarrow \mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K x_{ijk} \le E\left( {\tilde{a}_i }\right) \\&\Rightarrow \mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K x_{ijk} \le E\left( \left( {a_{i1}^U ,a_{i2}^U ,a_{i3}^U ,a_{i4}^U ;H_1 \left( {a_i^U } \right) \!, H_2 \left( {a_i^U } \right) } \right) \!,\right. \\&\quad \left. \left( {a_{i1}^L ,a_{i2}^L ,a_{i3}^L ,a_{i4}^L ;H_1 \left( {a_i^L } \right) \!, H_2 \left( {a_i^L } \right) } \right) \right) \\&\Rightarrow \mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K x_{ijk} \le \frac{1}{8}\left( {a_{i1}^U +a_{i2}^U +a_{i3}^U +a_{i4}^U +a_{i1}^L +a_{i2}^L +a_{i3}^L +a_{i4}^L } \right) \\&\quad \times \frac{1}{4}\left( {H_1 \left( {a_i^U } \right) +H_2 \left( {a_i^U } \right) +H_1 \left( {a_i^L } \right) +H_2 \left( {a_i^L } \right) }\right) \end{aligned}$$

In the same way the other two fuzzy based inequality constraints of model-II converts to its equivalent form given by Eqs. (20) and (21) below.

$$\begin{aligned} \mathop {\sum }\limits _{j=1}^N \mathop {\sum }\limits _{k=1}^K x_{ijk}\ge & {} \frac{1}{8}\left( {b_{j1}^U +b_{j2}^U +b_{j3}^U +b_{j4}^U +b_{j1}^L +b_{j2}^L +b_{j3}^L +b_{j4}^L } \right) \nonumber \\&\times \frac{1}{4}\left( {H_1 \left( {b_j^U } \right) +H_2 \left( {b_j^U } \right) +H_1 \left( {b_j^L } \right) +H_2 \left( {b_j^L } \right) } \right) \end{aligned}$$
(20)
$$\begin{aligned} \mathop {\sum }\limits _{i=1}^M \mathop {\sum }\limits _{j=1}^N x_{ijk}\le & {} \frac{1}{8}\left( {e_{k1}^U +e_{k2}^U +e_{k3}^U +e_{k4}^U +e_{k1}^L +e_{k2}^L +e_{k3}^L +e_{k4}^L } \right) \nonumber \\&\times \frac{1}{4}\left( {H_1 \left( {e_k^U } \right) +H_2 \left( {e_k^U } \right) +H_1 \left( {e_k^L } \right) +H_2 \left( {e_k^L } \right) }\right) \end{aligned}$$
(21)

Numerical Illustration

To solve the proposed model-I and model-II, we use the following numerical data given by the Table 1 and Table 2 respectively.

Table 1 Different inputs of objective functions for model-I and model-II
Full size table
Table 2 Inputs for different parameters of solid transportation problem, model-I and model-II
Full size table

Optimal Results of Model-I and Model-II

With the data given by the Tables 1 and 2, both the model-I and model-II are solved by employing the Interactive fuzzy satisficing technique and results are obtained which are presented in Tables 3 and 4 respectively.

Table 3 Iterations for the both models
Full size table
Table 4 Optimal results for the model-I and model-II (M-Pareto optimal solution)
Full size table

Discussion and Managerial Insight

From the Table 4, it observed that, the objective value \(f_1\) and \(f_2\) for the model-II is greater than the objective value of model-I. For profit maximization problem the maximum objective value gives the maximum profit, which implies the model-II gives the maximum profit compare to the model-I. So it is clear that for a profit maximization solid transportation problem the profit become maximum when the parameters of transportation are fuzzy in nature.

This present investigation in field of transporting amount from its source point to the different destinations using different mode of transportation, reveals that the model-II is more acceptable compare to the model-I. In model-II, we have all the parameters as interval type-2 fuzzy number whereas in model-I the parameters of the objective functions are interval type-2 fuzzy in nature and the capacities of source, demand and conveyance considered as crisp. In real life the uncertainty occurs often is transportation system. In such situation the decision makers (DM) will be profitable by the present investigation.

Comparison with Earlier Work

As per literature survey solid transportation problem with profit maximization case is very rare. Also in most of the previous work researcher have investigated cost minimization. But in our investigation, we have maximize the profit. These two things are opposite to each other. So comparison between this two is not likely. Another thing, in our research we have attempt for the first time a profit maximizing and time minimizing solid transportation problem with trapezoidal interval type-2 fuzzy sets. Ultimately this work is totally a new investigation towards this fields as per our knowledge.

Conclusions and Future Scope

In this paper, we formulate a solid transportation problem with supply, demand, conveyance capacity, unit selling price, unit purchase cost, unit transportation cost and time of transportation are all considered as trapezoidal interval type-2 fuzzy numbers. And most important fact about this problem is that, it is having two objective functions, one is to maximize the profit while the other is to minimize the transportation time. The transportation problem so formulated is being solved by employing the Interactive Fuzzy Satisficing Method. In the present study the problems were solved using LINGO 13.0 software.

The main aspects of this research in the field of solid transportation problem can be summarized as follows.

  • As far as known, it is being the first attempt to formulate such type of a solid transportation problem involving profit maximization and time minimization.

  • Solution is based on an interactive satisficing method, which is a new approach for solution of such type of problems.

  • Interval type-2 fuzzy values give more precise values than the general type-1 fuzzy values. Thus DM is able to take more appropriate precise decisions with the help of present analysis.

From here, one can think of applying this concept and formulate new solid transportation such as, to maximize profit, minimize transportation time and having budget constraint, deteriorating item, price discount and also one can consider the safety factor and so on. Also this model can be solved in various environments like rough environment, fuzzy rough environment, intuitionistic fuzzy environment etc.