A global asymptotical stable control scheme for a Hexverter in fractional frequency transmission systems

Abstract

A fractional frequency transmission system (FFTS) is the most competitive choice for long distance transmission of offshore wind power, while the Hexverter, as a newly proposed direct AC/AC converter, is an attractive choice for its power conversion. This paper proposes a novel control scheme characterizing the global stability and strong robustness of the Hexverter in FFTS applications, which are based on the interconnection and dam** assignment passivity-based control (IDA-PBC) methodology. Firstly, the frequency decoupled model of the Hexverter is studied and then a port-controlled Hamiltonian (PCH) model is built. On this basis, the IDA-PB control scheme of the Hexverter is designed. Considering the interference of system parameters and unmodeled dynamics, integrators are added to the IDA-PB controller to eliminate the steady-state error. In addition, the voltage-balancing control is applied in order to balance the capacitor DC voltages to obtain a better performance. Finally, the simulation results and experimental results are presented to verify the effectiveness and superiority of the IDA-PB controller.

1 Introduction

Recently, offshore wind power has attracted more and more attention due to its greater superiority including rich resources, high efficiency, no land occupation, etc. As to the development of offshore wind power, the important technical issue that remains to be discussed is its grid integration. Currently, there are three main transmission technologies for connecting the offshore wind farm to the grid [1]: high voltage AC (HVAC) transmission system, high voltage DC (HVDC) transmission system and fractional frequency transmission system (FFTS).

The HVAC transmission system has the advantages of low cost and simple structure. But it cannot be applied over long distances due to its large charging current along the submarine cable [2]. At present, the widely-used wind power integration strategy is the flexible HVDC system, of which the two terminals are connected by the high-voltage high-power converter such as the modular multilevel converter (MMC) through a DC transmission line [3,4,5]. However, the HVDC system needs an offshore converter station which will lead to high costs for construction and maintenance, and it is difficult to deal with the fault cases [6]. In order to overcome the shortcomings of the HVDC system, the FFTS is proposed, in which the offshore wind farm and offshore transmission system works at a relatively low frequency [7,8,9]. FFTS is demonstrated to be the most competitive choice for long distance transmission of offshore wind power since the charging current can be greatly reduced and the technical performance as well as economic performance can be greatly improved compared to HVAC and HVDC systems [10].

The key equipment in the FFTS is the high-voltage high-power AC/AC converter. The modular multilevel matrix converter (M3C) is put forward by Erickson and Al-Naseem in 2001 [11], which has nine branches and connects two AC systems directly without a DC line. Researchers have done a great deal of study on the control strategies of M3C [12,13,14,15]. Although the M3C is a feasible topology, the nine branches lead to high cost and the numerous circulating current paths also increase the difficulties of circulating current analysis and suppression [16]. In 2011, Baruschka and Mertens proposed a new direct AC/AC topology called the Hexverter. Compared to M3C, it reduced the number of branches to six and only has one circulating current path [17], hence the equipment volume and cost are significantly reduced. In addition, this topology is quite suitable for connecting two different frequency systems since the coupling level of the connected system is weakened. Therefore, the Hexverter is a better choice for the FFTS.

Most researches on the Hexverter focus on the medium-voltage or low-voltage applications such as motor-drivers [18,19,20], and the generally adopted control scheme for the Hexverter is the vector control [21,22,23]. There are few researches which applied the Hexverter on a transmission system. Reference [24] applies the Hexverter to offshore wind power integration via FFTS and the vector control scheme of the Hexverter has been discussed in detail. However, while the performance of this scheme relies on the precise system model, it may deteriorate with considerable interference of system parameters. Moreover, the tuning of proportional-integral (PI) parameters to assure global stability is also tough work. Since stability is the primary problem of a power system, it is of great significance to do research on control schematics emphasizing stability. The interconnection and dam** assignment passivity-based control (IDA-PBC) is an effective controller design methodology for a non-linear system [25, 26]. By establishing the port-controlled Hamiltonian (PCH) model of the system and properly configuring the interconnection matrix as well as dam** matrix, it can keep the system global asymptotically stable and significantly improve the transient performance of the system. It is a novel attempt to develop the IDA-PBC scheme of the Hexverter for FFTS applications.

This paper focuses on the design of the novel control scheme of the Hexverter for FFTS based on IDA-PBC methodology. First, a brief introduction of IDA-PBC theory is given in Section 2. In section 3, the detail frequency decoupled model of the Hexverter is derived, and then the PCH model is established. On this basis, Section 4 proposes the global asymptotical control scheme and the detail design process of an IDA-PB controller is presented. Integral action is also studied to eliminate any steady-state error. Section 5 and Section 6 present simulation results and experimental results respectively to verify the validity of the proposed control scheme. Concluding remarks are presented in Section 7.

2 Overview of IDA-PBC methodology

The PCH system is a class of generalized passive systems which contain most of the practical physical systems. The lumped parameter PCH systems that have independent energy storage elements can be represented as:

$$\left\{ {\begin{array}{*{20}l} {{\text{d}}{\varvec{x}}/{\text{d}}t = \left[ {{\varvec{J}}\left( {\varvec{x}} \right) - {\varvec{R}}\left( {\varvec{x}} \right)} \right]{{(\partial H\left( {\varvec{x}} \right)} \mathord{\left/ {\vphantom {{(\partial H\left( {\varvec{x}} \right)} {\partial {\mathbf{x}}}}} \right. \kern-0pt} {\partial {\varvec{x}}}}) + {\varvec{g}}\left( {\varvec{x}} \right){\varvec{u}}} \hfill \\ {{\varvec{y}} = {\varvec{g}}^{\text{T}} \left( {\varvec{x}} \right){{(\partial H\left( {\varvec{x}} \right)} \mathord{\left/ {\vphantom {{(\partial H\left( {\varvec{x}} \right)} {\partial {\varvec{x}}}}} \right. \kern-0pt} {\partial {\varvec{x}}}})} \hfill \\ \end{array} } \right.$$

(1)

where ${\varvec{x}} \in {\mathbf{R}}^{{{n}}}$ is the state vector; ${\varvec{u}},{\varvec{y}} \in {\mathbf{R}}^{{{m}}}$ are the port power vectors that indicate the energy exchange between the system and the external environment; the scalar function $H ({\varvec{x}} )\ge 0$ is the stored energy of the system; ${\varvec{J}}({\varvec{x}})$ is an $n \times n$ antisymmetric matrix that indicates the internal interconnection structure; ${\varvec{R}}({\varvec{x}})$ is a symmetric matrix that represents internal dissipation; and ${\varvec{g}}\left( {\varvec{x}} \right)$ is an $n \times m$ input matrix that indicates the port interconnection structure. ${\varvec{J}}({\varvec{x}})$ and ${\varvec{R}}({\varvec{x}})$ are interconnection matrix and dam** matrix.

The aim of the IDA-PBC method is to find a state feedback ${\varvec{u}} = {\varvec{\beta}}({\varvec{x}})$ ensuring that the closed-loop system remains to be a PCH system as shown below:

$${\text{d}}{\varvec{x}}/{\text{d}}t = \left[ {{\varvec{J}}_{d} \left( {\varvec{x}} \right) - {\varvec{R}}_{d} \left( {\varvec{x}} \right)} \right]({{\partial H_{d} \left( {\varvec{x}} \right)} \mathord{\left/ {\vphantom {{\partial H_{d} \left( {\varvec{x}} \right)} {\partial {\varvec{x}}}}} \right. \kern-0pt} {\partial {\varvec{x}}}})$$

(2)

where $H_{d} ({\varvec{x}})$ is the closed-loop energy function, obtains minimum value at equilibrium ${\varvec{x}}^{{{*}}}$, the matrixes ${\varvec{J}}_{d} ({\varvec{x}} )= - {\varvec{J}}_{d}^{\text{T}} ({\varvec{x}})$ and ${\varvec{R}}_{d} ({\varvec{x}}) = - {\varvec{R}}_{d}^{\text{T}} ({\varvec{x}})$ are the desired interconnection matrix and dam** matrix.

The detail content of the IDA-PBC methodology and related theorems are presented in [25, 26].

3 Mathematical model of Hexverter

3.1 Configuration of Hexverter

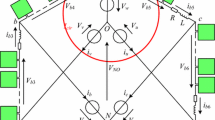
As shown in Fig. 1, the Hexverter has six branches that directly connect the two AC systems. $v_{u} ,\;v_{v} ,\;v_{w} ,\;i_{u} ,\;i_{v} \;,i_{w}$ are the voltages and currents of input system, $v_{a} ,\;v_{b} ,\;v_{c} ,\;i_{a} ,\;i_{b} \;,i_{c}$ are the voltages and currents of output system. The input frequency is f_s and the output frequency is f_l. Each branch consists of N H-bridge submodules, a resistor R and an inductor L. For each submodule, the output voltage can be three levels (±v_c and 0, v_c is the capacitor voltage). Therefore, the output voltage of N submodules can range from –Nv_c to Nv_c and can be considered as a voltage-controlled voltage source whose voltage is v_bk (k=1,2,…,6). Define expressions with subscript “$s$” to represent the variables of input system, “$l$” to represent the variables of output system, “$b$” to represent the variables of branches later in this paper.

Fig. 1

Configuration of the Hexverter

3.2 Decoupled model of Hexverter

Assuming that the voltage between the neutral points of the two AC systems is v_NO, the following equations can be determined from Fig. 1:

$$\left\{ \begin{aligned} v_{u} = Ri_{b1} + Lpi_{b1} + v_{b1} + v_{a} + v_{NO} \hfill \\ v_{v} = Ri_{b3} + Lpi_{b3} + v_{b3} + v_{b} + v_{NO} \hfill \\ v_{w} = Ri_{b5} + Lpi_{b5} + v_{b5} + v_{c} + v_{NO} \hfill \\ v_{a} = Ri_{b2} + Lpi_{b2} + v_{b2} + v_{v} - v_{NO} \hfill \\ v_{b} = Ri_{b4} + Lpi_{b4} + v_{b4} + v_{w} - v_{NO} \hfill \\ v_{c} = Ri_{b6} + Lpi_{b6} + v_{b6} + v_{u} - v_{NO} \hfill \\ \end{aligned} \right.$$

(3)

$$\left\{ \begin{aligned} i_{u} = i_{b1} - i_{b6} \hfill \\ i_{v} = i_{b3} - i_{b2} \hfill \\ i_{w} = i_{b5} - i_{b4} \hfill \\ i_{a} = i_{b1} - i_{b2} \hfill \\ i_{b} = i_{b3} - i_{b4} \hfill \\ i_{c} = i_{b5} - i_{b6} \hfill \\ \end{aligned} \right.$$

(4)

where $p = {\text{d}}/{\text{d}}t$ is the differential operator. When both systems are three-wire and symmetrical, the voltages and currents satisfy:

$$\left\{ {\begin{array}{*{20}l} {i_{u} { + }i_{v} { + }i_{w} =i_{a} { + }i_{b} { + }i_{c} = 0} \hfill \\ {i_{b1} + i_{b3} + i_{b5} = i_{b2} + i_{b4} + i_{b6} } \hfill \\ \end{array} } \right.$$

(5)

$$(v_{b1} + v_{b3} + v_{b5} ) - (v_{b2} + v_{b4} + v_{b6} ) + 6v_{NO} = 0$$

(6)

According to (3) and (4), there are two frequency components in the branch voltages and currents as well as the input and output currents. It causes inconvenience for analysis and control of the converter. Thus, frequency decoupling is necessary.

• 1) AC dynamic equations

  Pre-multiply (3) by the transformation matrix C_abc/αβ0 to obtain the voltage equations in the αβ0 reference frame:

  $$\left\{ {\begin{array}{*{20}l} {v_{s\alpha } = Ri_{b\alpha 1} + Lpi_{b\alpha 1} + v_{b\alpha 1} + v_{l\alpha } } \hfill \\ {v_{s\beta } = Ri_{b\beta 1} + Lpi_{b\beta 1} + v_{b\beta 1} + v_{l\beta } } \hfill \\ {v_{s0} = Ri_{b01} + Lpi_{b01} + v_{b01} + v_{l0} + \sqrt 3 v_{NO} } \hfill \\ {v_{l\alpha } = Ri_{b\alpha 2} + Lpi_{b\alpha 2} + v_{b\alpha 2} - {{v_{s\alpha } } \mathord{\left/ {\vphantom {{v_{s\alpha } } 2}} \right. \kern-0pt} 2} + {{\sqrt 3 v_{s\beta } } \mathord{\left/ {\vphantom {{\sqrt 3 v_{s\beta } } 2}} \right. \kern-0pt} 2}} \hfill \\ {v_{l\beta } = Ri_{b\beta 2} + Lpi_{b\beta 2} + v_{b\beta 2} - {{\sqrt 3 v_{s\alpha } } \mathord{\left/ {\vphantom {{\sqrt 3 v_{s\alpha } } 2}} \right. \kern-0pt} 2} - {{v_{s\beta } } \mathord{\left/ {\vphantom {{v_{s\beta } } 2}} \right. \kern-0pt} 2}} \hfill \\ {v_{l0} = Ri_{b02} + Lpi_{b02} + v_{b02} + v_{s0} - \sqrt 3 v_{NO} } \hfill \\ \end{array} } \right.$$

  (7)

  where subscript “1” indicates the variables of branches 1, 3, 5 and subscript “2” indicates the variables of branches 2, 4, 6. Considering the general conditions, divide the variables which contain the two frequency components into the form below:

  $$\left\{ {\begin{array}{*{20}l} {i_{s\alpha } =i_{s\alpha ,fs} + i_{s\alpha ,fl} } \hfill \\ {i_{s\beta } = i_{s\beta ,fs} + i_{s\beta ,fl} } \hfill \\ {i_{b\alpha 1} = i_{b\alpha 1,fs} + i_{b\alpha 1,fl} } \hfill \\ {i_{b\beta 1} =i_{b\beta 1,fs} + i_{b\beta 1,fl} } \hfill \\ {v_{b\alpha 1} = v_{b\alpha 1,fs} + v_{b\alpha 1,fl} } \hfill \\ {v_{b\beta 1} = v_{b\beta 1,fs} + v_{b\beta 1,fl} } \hfill \\ {i_{l\alpha } =i_{l\alpha ,fs} + i_{l\alpha ,fl} } \hfill \\ {i_{l\beta } = i_{l\beta ,fs} + i_{l\beta ,fl} } \hfill \\ {i_{b\alpha 2} =i_{b\alpha 2,fs} + i_{b\alpha 2,fl} } \hfill \\ {i_{b\beta 2} =i_{b\beta 2,fs} + i_{b\beta 2,fl} } \hfill \\ {v_{b\alpha 2} = v_{b\alpha 2,fs} + v_{b\alpha 2,fl} } \hfill \\ {v_{b\beta 2} = v_{b\beta 2,fs} + v_{b\beta 2,fl} } \hfill \\ \end{array} } \right.$$

  (8)

  where subscript “fs” indicates the variables containing input frequency component; “fl” indicates the variables containing output frequency component. Substitute (8) into (7) and separate the equations in terms of frequency:

  $$\left\{ {\begin{array}{*{20}l} {v_{s\alpha } = Ri_{b\alpha 1,fs} + Lpi_{b\alpha 1,fs} + v_{b\alpha 1,fs} } \hfill \\ {v_{s\beta } = Ri_{b\beta 1,fs} + Lpi_{b\beta 1,fs} + v_{b\beta 1,s} } \hfill \\ {0 = Ri_{b\alpha 1,fl} + Lpi_{b\alpha 1,fl} + v_{b\alpha 1,fl} + v_{l\alpha } } \hfill \\ {0 = Ri_{b\beta 1,fl} + Lpi_{b\beta 1,fl} + v_{b\beta 1,fl} + v_{l\beta } } \hfill \\ {v_{l\alpha } = Ri_{b\alpha 2,fl} + Lpi_{b\alpha 2,fl} + v_{b\alpha 2,fl} } \hfill \\ {v_{l\beta } = Ri_{b\beta 2,fl} + Lpi_{b\beta 2,fl} + v_{b\beta 2,fl} } \hfill \\ {0 = Ri_{b\alpha 2,fs} + Lpi_{b\alpha 2,fs} + v_{b\alpha 2,fs} - {{v_{s\alpha } } \mathord{\left/ {\vphantom {{v_{s\alpha } } 2}} \right. \kern-0pt} 2} + {{\sqrt 3 v_{s\beta } } \mathord{\left/ {\vphantom {{\sqrt 3 v_{s\beta } } 2}} \right. \kern-0pt} 2}} \hfill \\ {0 = Ri_{b\beta 2,fs} + Lpi_{b\beta 2,fs} + v_{b\beta 2,fs} - {{\sqrt 3 v_{s\alpha } } \mathord{\left/ {\vphantom {{\sqrt 3 v_{s\alpha } } 2}} \right. \kern-0pt} 2} - {{v_{s\beta } } \mathord{\left/ {\vphantom {{v_{s\beta } } 2}} \right. \kern-0pt} 2}} \hfill \\ \end{array} } \right.$$

  (9)

  Apply the dq transformation to (9), and write the equations in matrix form:

  $$\left\{ \begin{aligned} \left[ {\begin{array}{*{20}c} {v_{sd} } \\ {v_{sq} } \\ \end{array} } \right] = R\left[ {\begin{array}{*{20}c} {i_{bd1,fs} } \\ {i_{bq1,fs} } \\ \end{array} } \right] + Lp\left[ {\begin{array}{*{20}c} {i_{bd1,fs} } \\ {i_{bq1,fs} } \\ \end{array} } \right] + \omega_{s} L\left[ {\begin{array}{*{20}c} { - i_{bq1,fs} } \\ {i_{bd1,fs} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {v_{bd1,fs} } \\ {v_{bq1,fs} } \\ \end{array} } \right] \\ - \left[ {\begin{array}{*{20}c} {v_{ld} } \\ {v_{lq} } \\ \end{array} } \right] = R\left[ {\begin{array}{*{20}c} {i_{bd1,fl} } \\ {i_{bq1,fl} } \\ \end{array} } \right] + Lp\left[ {\begin{array}{*{20}c} {i_{bd1,fl} } \\ {i_{bq1,fl} } \\ \end{array} } \right] + \omega_{l} L\left[ {\begin{array}{*{20}c} { - i_{bq1,fl} } \\ {i_{bd1,fl} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {v_{bd1,fl} } \\ {v_{bq1,fl} } \\ \end{array} } \right] \\ {\varvec{A}}\left[ {\begin{array}{*{20}c} {v_{sd} } \\ {v_{sq} } \\ \end{array} } \right] = R\left[ {\begin{array}{*{20}c} {i_{bd2,fs} } \\ {i_{bq2,fs} } \\ \end{array} } \right] + Lp\left[ {\begin{array}{*{20}c} {i_{bd2,fs} } \\ {i_{bq2,fs} } \\ \end{array} } \right] + \omega_{s} L\left[ {\begin{array}{*{20}c} { - i_{bq2,fs} } \\ {i_{bd2,fs} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {v_{bd2,fs} } \\ {v_{bq2,fs} } \\ \end{array} } \right] \\ \left[ {\begin{array}{*{20}c} {v_{ld} } \\ {v_{lq} } \\ \end{array} } \right] = R\left[ {\begin{array}{*{20}c} {i_{bd2,fl} } \\ {i_{bq2,fl} } \\ \end{array} } \right] + Lp\left[ {\begin{array}{*{20}c} {i_{bd2,fl} } \\ {i_{bq2,fl} } \\ \end{array} } \right] + \omega_{l} L\left[ {\begin{array}{*{20}c} { - i_{bq2,fl} } \\ {i_{bd2,fl} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {v_{bd2,fl} } \\ {v_{bq2,fl} } \\ \end{array} } \right] \\ \end{aligned} \right.$$

  (10)

  where ${\varvec{A}} = \left[ {\begin{array}{*{20}c} {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} & { - {{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } 2}} \right. \kern-0pt} 2}} \\ {{{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } 2}} \right. \kern-0pt} 2}} & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} \\ \end{array} } \right]$.

  Assuming i_b0= i_b01=i_b02, the equations of the zero components in (7) can be simplified as:

  $${{\left( {v_{b01} { + }v_{b02} } \right)} \mathord{\left/ {\vphantom {{\left( {v_{b01} { + }v_{b02} } \right)} 2}} \right. \kern-0pt} 2} = - Ri_{b0} - Lpi_{b0}$$

  (11)

  Apply the αβ0 and dq transformation to (4) and simplify, then the relationship of the current can be determined as:

  $$\left\{ {\begin{array}{*{20}l} {i_{sd,fs} = i_{bd1,fs} + {{i_{bd2,fs} } \mathord{\left/ {\vphantom {{i_{bd2,fs} } 2}} \right. \kern-0pt} 2} + \sqrt 3 {{i_{bq2,fs} } \mathord{\left/ {\vphantom {{i_{bq2,fs} } 2}} \right. \kern-0pt} 2}} \hfill \\ {i_{sq,fs} = i_{bq1,fs} - \sqrt 3 {{i_{bd2,fs} } \mathord{\left/ {\vphantom {{i_{bd2,fs} } 2}} \right. \kern-0pt} 2} + {{i_{bq2,fs} } \mathord{\left/ {\vphantom {{i_{bq2,fs} } 2}} \right. \kern-0pt} 2}} \hfill \\ {i_{ld,fs} = i_{bd1,fs} - i_{bd2,fs} } \hfill \\ {i_{lq,fs} = i_{bq1,fs} - i_{bq2,fs} } \hfill \\ {i_{sd,fl} = i_{bd1,fl} + {{i_{bd2,fl} } \mathord{\left/ {\vphantom {{i_{bd2,fl} } 2}} \right. \kern-0pt} 2} + \sqrt 3 {{i_{bq2,fl} } \mathord{\left/ {\vphantom {{i_{bq2,fl} } 2}} \right. \kern-0pt} 2}} \hfill \\ {i_{sq,fl} = i_{bq1,fl} - \sqrt 3 {{i_{bd2,fl} } \mathord{\left/ {\vphantom {{i_{bd2,fl} } 2}} \right. \kern-0pt} 2} + {{i_{bq2,fl} } \mathord{\left/ {\vphantom {{i_{bq2,fl} } 2}} \right. \kern-0pt} 2}} \hfill \\ {i_{ld,fl} = i_{bd1,fl} - i_{bd2,fl} } \hfill \\ {i_{lq,fl} = i_{bq1,fl} - i_{bq2,fl} } \hfill \\ \end{array} } \right.$$

  (12)

• 2) DC dynamic equations

  Considering that each submodule capacitor has basically the same charging and discharging process, N submodules of a branch can be equated to one module as shown in Fig. 2 and:

  $$\left\{ {\begin{array}{*{20}l} {v_{b} = Nm_{b} v_{dc}^{'} = m_{b} v_{dc} } \hfill \\ {i_{dc} = C^{'} {{p\left( {Nv_{dc}^{'} } \right)} \mathord{\left/ {\vphantom {{p\left( {Nv_{dc}^{'} } \right)} N}} \right. \kern-0pt} N} = {\text{C}}pv_{dc} = m_{b} i_{b} } \hfill \\ \end{array} } \right.$$

  (13)

  where $m_{b}$ is the branch modulation signal. For each branch:

  $$Cv_{dck} pv_{dck} = v_{dck} m_{bk} i_{bk} = v_{bk} i_{bk} \;\;\;k = 1,2, \ldots ,6$$

  (14)

  Let $3\overline{v}_{dc1} =\left( {v_{dc1} + v_{dc3} + v_{dc5} } \right)$ and $3\overline{v}_{dc2} =\left( {v_{dc2} + v_{dc4} + v_{dc6} } \right)$ to keep consistent with the AC dynamic equations, where $\overline{v}_{dc1}$, $\overline{v}_{dc2}$ are the average voltage of branches 1, 3, 5 and branches 2, 4, 6, respectively. The following equations can be determined:

  $$\left\{ {\begin{array}{*{20}l} {3C\overline{v}_{dc1} p\overline{v}_{dc1} = v_{b1} i_{b1} { + }v_{b3} i_{b3} { + }v_{b5} i_{b5} } \hfill \\ {3C\overline{v}_{dc2} p\overline{v}_{dc2} = v_{b2} i_{b2} { + }v_{b4} i_{b4} { + }v_{b6} i_{b6} } \hfill \\ \end{array} } \right.$$

  (15)

  Apply the αβ0 and dq transformation to (15). Generally, the capacitors of submodules are large enough to suppress the fluctuation of the DC voltage, so the (fs+fl) and (fs–fl) components are neglected in the process. The DC dynamic equation can be determined as:

  $$\left\{ \begin{aligned} & 3C\overline{v}_{dc1} p\overline{v}_{dc1} = \left( {v_{bsd1} i_{bd1,fs} { + }v_{bsq1} i_{bq1,fs} } \right) \\ & \quad \quad \quad \quad \quad { + }\left( {v_{bld1} i_{bd1,fl} { + }v_{blq1} i_{bq1,fl} } \right){ + }v_{b01} i_{b0} \\ & 3C\overline{v}_{dc2} p\overline{v}_{dc2} = \left( {v_{bsd2} i_{bd2,fs} { + }v_{bsq2} i_{bq2,fs} } \right) \\ & \quad \quad \quad \quad \quad { + }\left( {v_{bld2} i_{bd2,fl} { + }v_{blq2} i_{bq2,fl} } \right){ + }v_{b02} i_{b0} \\ \end{aligned} \right.$$

  (16)

  Equations (10), (11) and (16) compose the frequency decoupled mathematical model of the Hexverter.

  Fig. 2

  

  Equivalent circuit of series submodules in one branch

3.3 PCH model of Hexverter

As shown in Fig. 1, the Hexverter is a two-port circuit. The port power variables are ($v_{sd}$, $i_{sd,fs}$), ($v_{sq}$, $i_{sq,fs}$), (0, $i_{sd,fl}$), (0, $i_{sq,fl}$), (0, $- i_{ld,fs}$), (0, $- i_{lq,fs}$), ($v_{ld}$, $- i_{ld,fl}$), ($v_{lq}$, $- i_{lq,fl}$). Define $v_{sd} ,\;v_{sq} ,\;v_{ld} ,\;v_{lq}$ as the input port variables, $i_{sd,fs} ,\;i_{sq,fs} ,\; - i_{ld,fl} , - i_{lq,fl}$ as the output port variables (the current of the output side is negative due to the reference direction) and H as the energy function. H is expressed as:

$$\begin{aligned} H = \frac{1}{2}(Li_{bd1,fs}^{2} + Li_{bq1,fs}^{2} + Li_{bd1,fl}^{2} + Li_{bq1,fl}^{2} + Li_{bd2,fs}^{2} + \hfill \\ Li_{bq2,fs}^{2} + Li_{bd2,fl}^{2} + Li_{bq2,fl}^{2} + 2Li_{b0}^{2} + 3C\overline{v}_{dc1}^{2} + 3C\overline{v}_{dc2}^{2} ) \hfill \\ \end{aligned}$$

(17)

Thus, the frequency decoupled mathematical model of the Hexverter can be written in the form of the PCH model as shown in (1). The variables and matrixes are as follows:

$$\begin{array}{*{20}l} {{\varvec{x}} = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & {x_{3} } & {x_{4} } & {x_{5} } & {x_{6} } & {x_{7} } & {x_{8} } & {x_{9} } & {x_{10} } & {x_{11} } \\ \end{array} } \right]^{\text{T}} } \hfill \\ {\quad = \left[ {\begin{array}{*{20}c} {i_{bd1,fs} } & {i_{bq1,fs} } & {i_{bd1,fl} } & {i_{bq1,fl} } & {i_{bd2,fs} } & {i_{bq2,fs} } \\ \end{array} } \right.} \hfill \\ {\quad \left. {\begin{array}{*{20}c} {i_{bd2,fl} } & {i_{bq2,fl} } & {i_{b0} } & {\overline{v}_{dc1} } & {\overline{v}_{dc2} } \\ \end{array} } \right]^{\text{T}} } \hfill \\ \end{array}$$

$$\begin{array}{*{20}l} {{\varvec{u}} = \left[ {\begin{array}{*{20}c} {v_{sd} } & {v_{sq} } & {v_{ld} } & {v_{lq} } \\ \end{array} } \right]^{\text{T}} } \hfill \\ {{\varvec{y}} = \left[ {\begin{array}{*{20}c} {i_{sd,fs} } & {i_{sq,fs} } & { - i_{ld,fl} } & { - i_{lq,fl} } \\ \end{array} } \right]^{\text{T}} } \hfill \\ \end{array}$$

$${\varvec{J}} = \left[ {\begin{array}{*{20}c} 0 & {\frac{{\omega_{s} }}{L}} & {0} & {0} & {0} & {0} & {0} & {0} & {0} & { - \frac{{m_{bsd1} }}{3LC}} & {0} \\ { - \frac{{\omega_{s} }}{L}} & 0 & {0} & {0} & {0} & {0} & {0} & {0} & {0} & { - \frac{{m_{bsq1} }}{3LC}} & {0} \\ {0} & {0} & 0 & {\frac{{\omega_{l} }}{L}} & {0} & {0} & {0} & {0} & {0} & { - \frac{{m_{bld1} }}{3LC}} & {0} \\ {0} & {0} & { - \frac{{\omega_{l} }}{L}} & 0 & {0} & {0} & {0} & {0} & {0} & { - \frac{{m_{blq1} }}{3LC}} & {0} \\ {0} & {0} & {0} & {0} & 0 & {\frac{{\omega_{s} }}{L}} & {0} & {0} & {0} & {0} & { - \frac{{m_{bsd2} }}{3LC}} \\ {0} & {0} & {0} & {0} & { - \frac{{\omega_{s} }}{L}} & 0 & {0} & {0} & {0} & {0} & { - \frac{{m_{bsq2} }}{3LC}} \\ {0} & {0} & {0} & {0} & {0} & {0} & 0 & {\frac{{\omega_{l} }}{L}} & {0} & {0} & { - \frac{{m_{bld2} }}{3LC}} \\ {0} & {0} & {0} & {0} & {0} & {0} & { - \frac{{\omega_{l} }}{L}} & 0 & {0} & {0} & { - \frac{{m_{blq2} }}{3LC}} \\ {0} & {0} & {0} & {0} & {0} & {0} & {0} & {0} & 0 & { - \frac{{m_{b01} }}{6LC}} & { - \frac{{m_{b02} }}{6LC}} \\ {\frac{{m_{bsd1} }}{3LC}} & {\frac{{m_{bsq1} }}{3LC}} & {\frac{{m_{bld1} }}{3LC}} & {\frac{{m_{blq1} }}{3LC}} & {0} & {0} & {0} & {0} & {\frac{{m_{b01} }}{6LC}} & 0 & {0} \\ {0} & {0} & {0} & {0} & {\frac{{m_{bsd2} }}{3LC}} & {\frac{{m_{bsq2} }}{3LC}} & {\frac{{m_{bld2} }}{3LC}} & {\frac{{m_{blq2} }}{3LC}} & {\frac{{m_{b02} }}{6LC}} & {0} & 0 \\ \end{array} } \right]$$

$${\varvec{g}}^{\text{T}} = \left[ {\begin{array}{*{20}c} {{1 \mathord{\left/ {\vphantom {1 L}} \right. \kern-0pt} L}} & 0 & 0 & 0 & {{1 \mathord{\left/ {\vphantom {1 {2L}}} \right. \kern-0pt} {2L}}} & {{{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } {2L}}} \right. \kern-0pt} {2L}}} & 0 & 0 & 0 & 0 & 0 \\ 0 & {{1 \mathord{\left/ {\vphantom {1 L}} \right. \kern-0pt} L}} & {0} & {0} & { - {{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } {2L}}} \right. \kern-0pt} {2L}}} & {{1 \mathord{\left/ {\vphantom {1 {2L}}} \right. \kern-0pt} {2L}}} & {0} & {0} & {0} & {0} & {0} \\ 0 & {0} & { - {1 \mathord{\left/ {\vphantom {1 L}} \right. \kern-0pt} L}} & {0} & {0} & {0} & {{1 \mathord{\left/ {\vphantom {1 L}} \right. \kern-0pt} L}} & {0} & {0} & {0} & {0} \\ 0 & {0} & {0} & { - {1 \mathord{\left/ {\vphantom {1 L}} \right. \kern-0pt} L}} & {0} & {0} & {0} & {{1 \mathord{\left/ {\vphantom {1 L}} \right. \kern-0pt} L}} & {0} & {0} & {0} \\ \end{array} } \right]$$

$$\varvec{R} = {\text{diag}}\left[ {\begin{array}{*{20}c} {\frac{R}{{L^{2} }}} & {\frac{R}{{L^{2} }}} & {\frac{R}{{L^{2} }}} & {\frac{R}{{L^{2} }}} & {\frac{R}{{L^{2} }}} & {\frac{R}{{L^{2} }}} & {\frac{R}{{L^{2} }}} & {\frac{R}{{L^{2} }}} & {\frac{R}{{L^{2} }}} & 0 & 0 \\ \end{array} } \right]$$

Orient the dq reference frame with the grid voltage, the input vector can be determined as:

$${\varvec{u}} = \left[ {\begin{array}{*{20}c} {\sqrt {3/2} V_{sdm} } & 0 & {\sqrt {3/2} V_{ldm} } & 0 \\ \end{array} } \right]^{\text{T}}$$

(18)

where V_sdm and V_ldm are the amplitude of input and output voltages, respectively.

4 IDA-PBC method of Hexverter

4.1 Overview of control scheme

The overview of the control scheme of the Hexverter is presented in Fig. 3.

Fig. 3

Overview of control scheme of the Hexverter

The design process is as follows. Firstly, the reference values of the input and output currents can be determined by demand for the active and reactive power. Secondly, the current transformation according to (12) is implemented and the expected values of the branch currents are derived. Thirdly, dq transformation is applied to the actual values of the branch currents to obtain the state variables. Then the IDA-PBC method is adopted to obtain the modulation variables in the dq reference frame. Finally, transform the modulation variables to the abc reference frame, apply the carrier phase shifted modulation to generate the gate signals of the six branches. In addition, the voltage-balancing control is applied in order to balance the capacitor DC voltages of the N submodules in one branch.

4.2 IDA-PBC design

As shown in Fig. 3, the IDA-PB controller is the core of the control scheme. Being different from the traditional vector control method, it has no need to determine and optimize the PI parameters. Various types of IDA-PB controllers can be designed by solving modulation variables on the basis of the IDA-PBC methodology and configuring the interconnection matrix as well as the dam** matrix,

4.2.1 IDA-PB controller with constant interconnection structure

Define the expected asymptotically stable equilibrium point of the closed-loop as:

$$\begin{array}{*{20}l} {{\varvec{x}}^{{\mathbf{*}}} =\left[ {\begin{array}{*{20}c} {I_{bd1,fs} } & {I_{bq1,fs} } & {I_{bd1,fl} } & {I_{bq1,fl} } & {I_{bd2,fs} } & {I_{bq2,fs} } \\ \end{array} } \right.} \hfill \\ {\quad \quad \left. {\begin{array}{*{20}c} {I_{bd2,fl} } & {I_{bq2,fl} } & {I_{b0} } & {V_{dcr} } & {V_{dcr} } \\ \end{array} } \right]^{\text{T}} } \hfill \\ \end{array}$$

The expected interconnection matrix and dam** matrix of the closed-loop are:

$${\varvec{J}}_{d} = {\varvec{J}}$$

(19)

$${\varvec{R}}_{d} = {\varvec{R}} + {\varvec{R}}_{a}$$

(20)

where R_a is the proposed injected dam** matrix:

$${\varvec{R}}_{a} = \left[ {\begin{array}{*{20}c} {r_{1} } & {0} & {0} & {0} & {0} & {0} & {0} & {0} & {0} & {r_{16} } & {0} \\ {0} & {r_{2} } & {0} & {0} & {0} & {0} & {0} & {0} & {0} & {r_{17} } & {0} \\ {0} & {0} & {r_{3} } & {0} & {0} & {0} & {0} & {0} & {0} & {r_{18} } & {0} \\ {0} & {0} & {0} & {r_{4} } & {0} & {0} & {0} & {0} & {0} & {r_{19} } & {0} \\ {0} & {0} & {0} & {0} & {r_{5} } & {0} & {0} & {0} & {0} & {0} & {r_{24} } \\ {0} & {0} & {0} & {0} & {0} & {r_{6} } & {0} & {0} & {0} & {0} & {r_{25} } \\ {0} & {0} & {0} & {0} & {0} & {0} & {r_{7} } & {0} & {0} & {0} & {r_{26} } \\ {0} & {0} & {0} & {0} & {0} & {0} & {0} & {r_{8} } & {0} & {0} & {r_{27} } \\ {0} & {0} & {0} & {0} & {0} & {0} & {0} & {0} & {r_{9} } & {r_{29} } & {r_{31} } \\ {r_{12} } & {r_{13} } & {r_{14} } & {r_{15} } & {0} & {0} & {0} & {0} & {r_{28} } & {r_{10} } & {0} \\ {0} & {0} & {0} & {0} & {r_{20} } & {r_{21} } & {r_{22} } & {r_{23} } & {r_{30} } & {0} & {r_{11} } \\ \end{array} } \right]$$

For general solutions, if R_a is an asymmetric matrix, the interconnection structure of the closed-loop needs to be changed. Under these circumstances, the original R_a can be represented as a sum of two matrixes: symmetric matrix and antisymmetric matrix. Here, in order to obtain an IDA-PB controller with constant interconnection structure, R_a should be a symmetric matrix, and the elements of the antisymmetric matrix should be zero. Then the energy function of the closed-loop H_d can be designed as the quadric form:

$$\begin{aligned} H_{d} = & \frac{1}{2}\left[ {L\left( {i_{bd1,fs} - I_{bd1,fs} } \right)^{2} + L\left( {i_{bq1,fs} - I_{bq1,fs} } \right)^{2} } \right. \\ & + L\left( {i_{bd1,fl} - I_{bd1,fl} } \right)^{2} + L\left( {i_{bq1,fl} - I_{bq1,fl} } \right)^{2} \\ & + L\left( {i_{bd2,fs} - I_{bd2,fs} } \right)^{2} + L\left( {i_{bq2,fs} - I_{bq2,fs} } \right)^{2} \\ & + L\left( {i_{bd2,fl} - I_{bd2,fl} } \right)^{2} + L\left( {i_{bq2,fl} - I_{bq2,fl} } \right)^{2} \\ & + 2L\left( {i_{b0} - I_{b0} } \right)^{2} + 3C\left. {\left( {\overline{v}_{dc1} - V_{dcr} } \right)^{2} + 3C\left( {\overline{v}_{dc2} - V_{dcr} } \right)^{2} } \right] \\ \end{aligned}$$

(21)

Therefore, the K(x) can be derived by:

$${\varvec{K}}({\varvec{x}}) = \partial H_{a} \left( {\varvec{x}} \right) /\partial {\varvec{x}}=\partial \left( {H_{d} - H} \right)\left( {\varvec{x}} \right)/\partial {\varvec{x}}$$

(22)

where K(x) is a column vector and its elements are defined as K_i (i =1,2,…,11).

According to the IDA-PBC methodology, eleven equations can be derived. Then, the ten modulation variables and the constraint of the dam** factors can be solved. Eight of the modulation variables are expressed in (23)–(30):

$$\begin{aligned} m_{bsd1} = & {{ - \left[ {L^{2} r_{1} \left( {I_{bd1,fs} - x_{1} } \right) + 3CLr_{16} \left( {V_{dcr} - x_{10} } \right)} \right]} \mathord{\left/ {\vphantom {{ - \left[ {L^{2} r_{1} \left( {I_{bd1,fs} - x_{1} } \right) + 3CLr_{16} \left( {V_{dcr} - x_{10} } \right)} \right]} {V_{dcr} }}} \right. \kern-0pt} {V_{dcr} }} \\ & {{ - \left( {RI_{bd1,fs} - \omega_{s} LI_{bq1,fs} - \sqrt {3/2} V_{sdm} } \right)} \mathord{\left/ {\vphantom {{ - \left( {RI_{bd1,fs} - \omega_{s} LI_{bq1,fs} - \sqrt {3/2} V_{sdm} } \right)} {V_{dcr} }}} \right. \kern-0pt} {V_{dcr} }} \\ \end{aligned}$$

(23)

$$\begin{aligned} m_{bsq1} = & - {{\left[ {L^{2} r_{2} \left( {I_{bq1,fs} - x_{2} } \right) + 3CLr_{17} \left( {V_{dcr} - x_{10} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {L^{2} r_{2} \left( {I_{bq1,fs} - x_{2} } \right) + 3CLr_{17} \left( {V_{dcr} - x_{10} } \right)} \right]} {V_{dcr} }}} \right. \kern-0pt} {V_{dcr} }} \\ & - {{\left( {RI_{bq1,fs} + \omega_{s} LI_{bd1,fs} } \right)} \mathord{\left/ {\vphantom {{\left( {RI_{bq1,fs} + \omega_{s} LI_{bd1,fs} } \right)} {V_{dcr} }}} \right. \kern-0pt} {V_{dcr} }} \\ \end{aligned}$$

(24)

$$\begin{aligned} m_{bld1} = & {{ - \left[ {L^{2} r_{3} \left( {I_{bd1,fl} - x_{3} } \right) + 3CLr_{18} \left( {V_{dcr} - x_{10} } \right)} \right]} \mathord{\left/ {\vphantom {{ - \left[ {L^{2} r_{3} \left( {I_{bd1,fl} - x_{3} } \right) + 3CLr_{18} \left( {V_{dcr} - x_{10} } \right)} \right]} {V_{dcr} }}} \right. \kern-0pt} {V_{dcr} }} \\ & - {{\left( {RI_{bd1,fl} - \omega_{l} LI_{bq1,fl} + \sqrt {3/2} V_{ldm} } \right)} \mathord{\left/ {\vphantom {{\left( {RI_{bd1,fl} - \omega_{l} LI_{bq1,fl} + \sqrt {3/2} V_{ldm} } \right)} {V_{dcr} }}} \right. \kern-0pt} {V_{dcr} }} \\ \end{aligned}$$

(25)

$$\begin{aligned} m_{blq1} = & - {{\left[ {L^{2} r_{4} \left( {I_{bq1,fl} - x_{4} } \right) + 3CLr_{19} \left( {V_{dcr} - x_{10} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {L^{2} r_{4} \left( {I_{bq1,fl} - x_{4} } \right) + 3CLr_{19} \left( {V_{dcr} - x_{10} } \right)} \right]} {V_{dcr} }}} \right. \kern-0pt} {V_{dcr} }} \\ & - {{\left( {RI_{bq1,fl} + \omega_{l} LI_{bd1,fl} } \right)} \mathord{\left/ {\vphantom {{\left( {RI_{bq1,fl} + \omega_{l} LI_{bd1,fl} } \right)} {V_{dcr} }}} \right. \kern-0pt} {V_{dcr} }} \\ \end{aligned}$$

(26)

$$\begin{aligned} m_{bsd2} = & - {{\left[ {L^{2} r_{5} \left( {I_{bd2,fs} - x_{5} } \right) + 3CLr_{24} \left( {V_{dcr} - x_{11} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {L^{2} r_{5} \left( {I_{bd2,fs} - x_{5} } \right) + 3CLr_{24} \left( {V_{dcr} - x_{11} } \right)} \right]} {V_{dcr} }}} \right. \kern-0pt} {V_{dcr} }} \\ & - {{\left( {RI_{bd2,fs} - \omega_{s} LI_{bq2,fs} - \sqrt 6 V_{sdm} /4} \right)} \mathord{\left/ {\vphantom {{\left( {RI_{bd2,fs} - \omega_{s} LI_{bq2,fs} - \sqrt 6 V_{sdm} /4} \right)} {V_{dcr} }}} \right. \kern-0pt} {V_{dcr} }} \\ \end{aligned}$$

(27)

$$\begin{aligned} m_{bsq2} = & - {{\left[ {L^{2} r_{6} \left( {I_{bq2,fs} - x_{6} } \right) + 3CLr_{25} \left( {V_{dcr} - x_{11} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {L^{2} r_{6} \left( {I_{bq2,fs} - x_{6} } \right) + 3CLr_{25} \left( {V_{dcr} - x_{11} } \right)} \right]} {V_{dcr} }}} \right. \kern-0pt} {V_{dcr} }} \\ & - {{\left( {RI_{bq2,fs} + \omega_{s} LI_{bd2,fs} - 3\sqrt 2 V_{sdm} /4} \right)} \mathord{\left/ {\vphantom {{\left( {RI_{bq2,fs} + \omega_{s} LI_{bd2,fs} - 3\sqrt 2 V_{sdm} /4} \right)} {V_{dcr} }}} \right. \kern-0pt} {V_{dcr} }} \\ \end{aligned}$$

(28)

$$\begin{aligned} m_{bld2} = & - {{\left[ {L^{2} r_{7} \left( {I_{bd2,fl} - x_{7} } \right) + 3CLr_{26} \left( {V_{dcr} - x_{11} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {L^{2} r_{7} \left( {I_{bd2,fl} - x_{7} } \right) + 3CLr_{26} \left( {V_{dcr} - x_{11} } \right)} \right]} {V_{dcr} }}} \right. \kern-0pt} {V_{dcr} }} \\ & - {{\left( {RI_{bd2,fl} - \omega_{l} LI_{bq2,fl} - \sqrt {3/2} V_{ldm} } \right)} \mathord{\left/ {\vphantom {{\left( {RI_{bd2,fl} - \omega_{l} LI_{bq2,fl} - \sqrt {3/2} V_{ldm} } \right)} {V_{dcr} }}} \right. \kern-0pt} {V_{dcr} }} \\ \end{aligned}$$

(29)

$$\begin{aligned} m_{blq2} = & - {{\left[ {L^{2} r_{8} \left( {I_{bq2,fl} - x_{8} } \right) + 3CLr_{27} \left( {V_{dcr} - x_{11} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {L^{2} r_{8} \left( {I_{bq2,fl} - x_{8} } \right) + 3CLr_{27} \left( {V_{dcr} - x_{11} } \right)} \right]} {V_{dcr} }}} \right. \kern-0pt} {V_{dcr} }} \\ & - {{\left( {RI_{bq2,fl} + \omega_{l} LI_{bd2,fl} } \right)} \mathord{\left/ {\vphantom {{\left( {RI_{bq2,fl} + \omega_{l} LI_{bd2,fl} } \right)} {V_{dcr} }}} \right. \kern-0pt} {V_{dcr} }} \\ \end{aligned}$$

(30)

Figure 4 depicts the control blocks diagram. The block for the fs components of branches 1, 3, 5 are shown in detail as an example. The other three blocks have similar structures which can be determined based on (25)–(30).

Fig. 4

Control blocks diagram

The solution to the other two modulation variables (m_b01 and m_b02) depends on the value of K₉.

• 1) If K₉=–2LI_b0≠ 0, m_b01 and m_b02 can be derived as:

  $$\begin{array}{*{20}l} {T_{3} m_{b01} ={{6T_{3} CLr_{28} \left( {I_{b0} - x_{9} } \right)} \mathord{\left/ {\vphantom {{6T_{3} CLr_{28} \left( {I_{b0} - x_{9} } \right)} {I_{b0} }}} \right. \kern-0pt} {I_{b0} }}{ + }9C^{2} V_{dcr} r_{10} \left( {V_{dcr} - x_{10} } \right)} \hfill \\ {\quad \quad \quad + \left[ {\left( {T_{1} r_{12} + L^{2} I_{bd1,fs} r_{1} } \right)\left( {I_{bd1,fs} - x_{1} } \right) + \left( {T_{1} r_{13} + L^{2} I_{bq1,fs} r_{2} } \right)\left( {I_{bq1,fs} - x_{2} } \right)} \right]} \hfill \\ {\quad \quad \quad + \left[ {\left( {T_{1} r_{14} + L^{2} I_{bd1,fl} r_{3} } \right)\left( {I_{bd1,fl} - x_{3} } \right) + \left( {T_{1} r_{15} + L^{2} I_{bq1,fl} r_{4} } \right)\left( {I_{bq1,fl} - x_{4} } \right)} \right]} \hfill \\ {\quad \quad \quad + \left( {T_{2} I_{bd1,fs} r_{16} + T_{2} I_{bq1,fs} r_{17} + T_{2} I_{bd1,fl} r_{18} + T_{2} I_{bq1,fl} r_{19} } \right)\left( {V_{dcr} - x_{10} } \right)} \hfill \\ {\quad \quad \quad + \left( {RI_{bd1,fs}^{2} + RI_{bd1,fl}^{2} + RI_{bq1,fs}^{2} + RI_{bq1,fl}^{2} } \right) - \left( {\sqrt {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}} V_{sdm} I_{bd1,fs} } \right.} \hfill \\ {\left. {\quad \quad \quad - \sqrt {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}} V_{ldm} I_{bd1,fl} } \right)} \hfill \\ \end{array}$$

  (31)
  $$\begin{array}{*{20}l} {T_{3} m_{b02} = 6T_{3} CLr_{30} {{\left( {I_{b0} - x_{9} } \right)} \mathord{\left/ {\vphantom {{\left( {I_{b0} - x_{9} } \right)} {I_{b0} }}} \right. \kern-0pt} {I_{b0} }} + 9C^{2} V_{dcr} r_{11} \left( {V_{dcr} - x_{11} } \right)} \hfill \\ {\quad \quad \quad + \left[ {\left( {T_{1} r_{20} + L^{2} I_{bd2,fs} r_{5} } \right)\left( {I_{bd2,fs} - x_{5} } \right) + \left( {T_{1} r_{21} + L^{2} I_{bq2,fs} r_{6} } \right)\left( {I_{bq2,fs} - x_{6} } \right)} \right]} \hfill \\ {\quad \quad \quad + \left[ {\left( {T_{1} r_{22} + L^{2} I_{bd2,fl} r_{7} } \right)\left( {I_{bd2,fl} - x_{7} } \right) + \left( {T_{1} r_{23} + L^{2} I_{bq2,fl} r_{8} } \right)\left( {I_{bq2,fl} - x_{8} } \right)} \right]} \hfill \\ {\quad \quad \quad + \left( {T_{2} I_{bd2,fs} r_{24} + T_{2} I_{bq2,fs} r_{25} + T_{2} I_{bd2,fl} r_{26} + T_{2} I_{bq2,fl} r_{27} } \right)\left( {V_{dcr} - x_{11} } \right)} \hfill \\ {\quad \quad \quad + \left( {RI_{bd2,fs}^{2} + R_{bd2,fl}^{2} + RI_{bq2,fs}^{2} + RI_{bq2,fl}^{2} } \right)} \hfill \\ {\quad \quad \quad - \left( {\frac{1}{2}\sqrt {\frac{3}{2}} V_{sdm} I_{bd2,fs} + \sqrt {\frac{3}{2}} V_{ldm} I_{bd2,fl} + \frac{\sqrt 3 }{2}\sqrt {\frac{3}{2}} V_{sdm} I_{bq2,fs} } \right)} \hfill \\ \end{array}$$

  (32)

  where $T_{1} = 3CLV_{dcr}$, $T_{2} = 3CL$, $T_{3} = I_{b0} V_{dcr}$.

  Substitute all the modulation variables into the redundant equation of the equation set to obtain the constraint equation of the dam** factors. Notice that R_a should be a symmetric matrix, the full constraints of dam** factors are:

  $$\left\{ {\begin{array}{*{20}l} {r_{16} = r_{12} = T_{4} I_{bd1,fs} r_{1} } \hfill \\ {r_{17} = r_{13} = T_{4} I_{bq1,fs} r_{2} } \hfill \\ {r_{18} = r_{14} = T_{4} I_{bd1,fl} r_{3} } \hfill \\ {r_{19} = r_{15} = T_{4} I_{bq1,fl} r_{4} } \hfill \\ {r_{24} = r_{20} = T_{4} I_{bd2,fs} r_{5} } \hfill \\ {r_{25} = r_{21} = T_{4} I_{bq2,fs} r_{6} } \hfill \\ {r_{26} = r_{22} = T_{4} I_{bd2,fl} r_{7} } \hfill \\ {r_{27} = r_{23} = T_{4} I_{bq2,fl} r_{8} } \hfill \\ {r_{28} = r_{29} , \, r_{30} = r_{31} } \hfill \\ {r_{30} { + }r_{28} = 2T_{4} I_{b0} r_{9} } \hfill \\ {r_{10} = T_{5} { + }2T_{4} I_{b0} r_{28} } \hfill \\ {r_{11} = T_{6} { + }2T_{4} I_{b0} r_{30} } \hfill \\ \end{array} } \right.$$

  (33)

  where

  $$\left\{ {\begin{array}{*{20}l} {T_{4} = - {L \mathord{\left/ {\vphantom {L {\left( {3CLV_{dcr} } \right)}}} \right. \kern-0pt} {\left( {3CLV_{dcr} } \right)}}} \hfill \\ {T_{5} = {{\left( {L^{2} I_{bd1,fs}^{2} r_{1} + L^{2} I_{bq1,fs}^{2} r_{2} + L^{2} I_{bd1,fl}^{2} r_{3} + L^{2} I_{bq1,fl}^{2} r_{4} } \right)} \mathord{\left/ {\vphantom {{\left( {L^{2} I_{bd1,fs}^{2} r_{1} + L^{2} I_{bq1,fs}^{2} r_{2} + L^{2} I_{bd1,fl}^{2} r_{3} + L^{2} I_{bq1,fl}^{2} r_{4} } \right)} {9C^{2} V_{dcr}^{2} }}} \right. \kern-0pt} {9C^{2} V_{dcr}^{2} }}} \hfill \\ {T_{6} = {{\left( {L^{2} I_{bd2,fs}^{2} r_{5} + L^{2} I_{bq2,fs}^{2} r_{6} + L^{2} I_{bd2,fl}^{2} r_{7} + L^{2} I_{bq2,fl}^{2} r_{8} } \right)} \mathord{\left/ {\vphantom {{\left( {L^{2} I_{bd2,fs}^{2} r_{5} + L^{2} I_{bq2,fs}^{2} r_{6} + L^{2} I_{bd2,fl}^{2} r_{7} + L^{2} I_{bq2,fl}^{2} r_{8} } \right)} {9C^{2} V_{dcr}^{2} }}} \right. \kern-0pt} {9C^{2} V_{dcr}^{2} }}} \hfill \\ \end{array} } \right.$$

• 2) If K₉=–2LI_b0=0, let m_b01=m_b02. Then it can be determined that:

  $$m_{b01} = m_{b02} = - 2L^{2} r_{9} {{\left( {I_{b0} - x_{9} } \right)} \mathord{\left/ {\vphantom {{\left( {I_{b0} - x_{9} } \right)} {V_{dcr} }}} \right. \kern-0pt} {V_{dcr} }}$$

  (34)

  On this occasion, the constraints for r₂₈-r₃₁, r₁₀ and r₁₁ will change to:

  $$\left\{ {\begin{array}{*{20}l} {r_{28} = r_{29} = 0} \hfill \\ {r_{30} = r_{31} = 0} \hfill \\ {r_{10} = T_{5} } \hfill \\ {r_{11} = T_{6} } \hfill \\ \end{array} } \right.$$

  (35)

  While the constraints for other factors are kept consistent with the situation where $K_{9} \ne 0$.

  The solution to modulation variables m_b01 and m_b02 can be illustrated as the flow diagram shown in Fig. 5.

  Fig. 5

  

  Flow diagram for solution to m_b01 and m_b02

  The expression of modulation variables can be simplified. And the dam** matrix of the closed-loop R_d can be determined by (20). To keep the system global asymptotical stable, R_d should be a positive definite matrix. Since the expressions of the tenth order principal minor and the determinant of R_d are excessively complicated, the range of dam** factors cannot be directly analytically solved. Here a numerical calculation is adopted to solve the dam** factors while ensuring that R_d is a positive definite.

4.2.2 IDA-PB controller with integrators

The IDA-PB controller with a constant interconnection structure can ensure that the whole system is asymptotically stable at the equilibrium point x^*. However, if the system parameters are inaccurate or there exist unmodeled dynamics, a steady-state error will arise. Thus, the IDA-PB controller with integrators is proposed to eliminate the steady-state error. The closed-loop system model with integrators can be expressed as:

$$\left\{ {\begin{array}{*{20}l} {\dot{\varvec{x}} = \left[ {{\varvec{J}}_{d} - {\varvec{R}}_{d} } \right]{{\partial H_{d} \left( \varvec{x} \right)} \mathord{\left/ {\vphantom {{\partial H_{d} \left( \varvec{x} \right)} {\partial \varvec{x}}}} \right. \kern-0pt} {\partial \varvec{x}}} + \varvec{v}} \hfill \\ {\dot{\varvec{v}} = - {\varvec{R}}_{I} {{\partial H_{d} \left( \varvec{x} \right)} \mathord{\left/ {\vphantom {{\partial H_{d} \left( \varvec{x} \right)} {\partial \varvec{x}}}} \right. \kern-0pt} {\partial \varvec{x}}}} \hfill \\ \end{array} } \right.$$

(36)

where R_I is a diagonal matrix with factors r_Ik(k=1,2,…,11) as diagonal elements. It means that the injected dam** factors r₁ to r₁₁ in R_a are changed to the form of (r_k+r_Ik/s). The state feedback is $\varvec{u} =\varvec{\beta}\left( \varvec{x} \right) + \varvec{v}$. Define the new closed-loop energy function as:

$$W\left( {\varvec{x},\varvec{v}} \right) = H_{d} \left( \varvec{x} \right) = \varvec{v}^{\text{T}} {\varvec{K}}_{I} {\varvec{v} \mathord{\left/ {\vphantom {\varvec{v} 2}} \right. \kern-0pt} 2}$$

(37)

where K_I is a diagonal matrix with factors 1/r_Ik(k=1,2,…,11) as its diagonal elements. It can be found that ${\varvec{R}}_{I} \nabla_{v} W = {\varvec{R}}_{I} {\varvec{K}}_{I} \varvec{v} = \varvec{v}$. Thus, the closed-loop system can be written in the PCH form:

$$\left[ {\begin{array}{*{20}c} {\dot{\varvec{x}}} \\ {\dot{\varvec{v}}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{J}}_{d} - {\varvec{R}}_{d} } & {{\varvec{R}}_{I} } \\ { - {\varvec{R}}_{I}^{\text{T}} } & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\nabla_{x} W} \\ {\nabla_{v} W} \\ \end{array} } \right]$$

(38)

To ensure that K_I is a positive definite matrix, it must be satisfied that r_Ik>0 (k=1,2,…,11). Then, all the conclusions about stability of the equilibrium point x^* remain preserved.

4.3 Voltage-balancing control

Take branch ua as an example. Figure 6 illustrates the control diagram of the voltage-balancing control and the modulation variable can be determined as:

Fig. 6

Voltage-balancing control diagram

$$m_{ua,i} = {{\left( {{{v_{ua} } \mathord{\left/ {\vphantom {{v_{ua} } N}} \right. \kern-0pt} N} + K_{C} i_{ua} (\bar{v}_{cua} - v_{cua,i} )} \right)} \mathord{\left/ {\vphantom {{\left( {{{v_{ua} } \mathord{\left/ {\vphantom {{v_{ua} } N}} \right. \kern-0pt} N} + K_{C} i_{ua} (\bar{v}_{cua} - v_{cua,i} )} \right)} {V_{dcr} }}} \right. \kern-0pt} {V_{dcr} }}\;\;\;\;i = 1,2, \ldots ,N$$

(39)

where v_ua is the modulating voltage of branch ua; $\bar{v}_{cua}$ is the reference DC voltage of each submodule capacitor; v_cua,i is the DC voltage of the capacitor i; and K_c is the proportional gain.

Assuming that the branch current is positive, if v_cua,i>$\bar{v}_{cua}$, the modulation variable will decrease. Thus the charging time of the capacitor i in one carrier cycle will be shortened to lower v_cua,i. The regulating process acts in a similar way when v_cua,i<$\bar{v}_{cua}$. It can be found that the modulation variables of the submodules in one branch are not identical and the DC voltage of each submodule is controlled to the reference voltage by this control method.

5 Simulation results

Figure 7 shows the configuration of the simulation model which has been built in a MATLAB/Simulink to verify the effectiveness of the IDA-PBC scheme. The offshore fractional frequency (FF) system is connected to the onshore Hexverter through a 50 km submarine cable and low frequency transformer. The main parameters of the system are listed in Table 1. The Hexverter operates as a unity power factor, both the q components of the input and output currents are controlled to zero.

Fig. 7

Configuration of FFTS based on the Hexverter

Table 1 Main parameters of simulation model

• 1) Simulation results of steady state

  The input and output currents, as shown in Fig. 8a and b, have good symmetry and the total harmonic distortions are 1.04% and 1.05%, respectively. It confirms that the designed IDA-PB controller has superior performance of steady state. Figure 8c and d present the current and voltage of branch ua as a representation of all branches. It can be seen that there are two different frequency components. As the output voltage of each submodule can be three levels (±v_c and 0) and each branch contains six submodules, it can be observed that the voltage shown in Fig. 8d has thirteen levels. Figure 8e verifies the effectiveness of the voltage-balancing control. With the voltage-balancing control added at t₁, the capacitor voltages coincide with each other in the fast regulation.

  Fig. 8

  

  Performance of steady-state control

• 2) Transient state simulation results

  In order to verify the transient performance of the IDA-PB controller, a step change of active power is set during the simulation process. Ensure the output active power drops from 10 MW to 5 MW at t₁=4 s and rises back to 10 MW at t₂=6 s. Some simulation results of the IDA-PB controlled system are presented in Fig. 9 in comparison with the results of the vector controlled system.

  Fig. 9

  

  Transient performance comparison of IDA-PBC and vector control

  Figure 9a shows the equivalent DC voltage of the branch capacitors. It can be observed that the DC voltage under the IDA-PBC almost remains unchanged, whereas the voltage under vector control shows drastic fluctuations when the power suddenly changes, which implies that the IDA-PB controller has a fast responding speed and good tracking performance. Figure 9b and c present the actual input and output power of the system and Fig. 9d and e present the d and q components of the input and output currents. The d current has the same changing tendency with its corresponding active power and the same conclusion is applicable to q current and reactive power. It can be seen that the input power or current under the IDA-PBC and vector control are approximately coincident, but the output power or current waveforms indicate that the IDA-PB controller has much better regulating ability.

• 3) Fault simulation results

  Ensure the input voltage drops from 10 kV to 6 kV at t₁=2 s to simulate a short-circuit fault. Figure 10 shows the simulation results. Also, the results of the vector-controlled system are presented as a comparison.

  Fig. 10

  

  Control performance comparison of IDA-PB controller and vector controller when voltage drops

  The waveforms of the input current in Fig. 10a illustrates that the system under IDA-PBC can be restored to steady state after a large disturbance. Figure 10b and c present the DC voltage and input power respectively. It can be observed that when the input voltage suddenly drops, the DC voltage under the IDA-PBC will restore in a short time after a small fluctuation and the input power can also restore to the reference value, whereas the system under vector control will have severe oscillation and lose stability. Therefore, the simulation results verify the effectiveness of the IDA-PB controller with integrators for enhancing system robustness.

6 Experiment results

Experimental results performed on the control-hardware-in-loop simulation platform (AppSIM) are presented here to reflect system performance. Figure 11 shows the structure of the experimental system, where the main circuit is built into the simulation computer, and the controller provides the gating signals. The currents and voltages are measured by the oscilloscope. The system parameters are consistent with the simulation model built in MATLAB/Simulink in Section 5, as shown in Table 1.

Fig. 11

Experiment system

Figure 12a, b, c show the input current, output current, and output power in steady-state respectively, from which we can see that they satisfy waveform quality. Figure 12d, e, f show the dynamic performance. The input and output current decrease smoothly as the active power drops from 10 MW to 5 MW, meanwhile the reactive power suffers little fluctuation. In conclusion, the IDA-PB controller of the Hexverter system has a satisfying performance.

Fig. 12

Experiment performance of the Hexverter system

7 Conclusion

This paper proposes a novel control scheme for a Hexverter with global asymptotical stability and strong robustness. A frequency decoupled model is built for the convenience of analysis and control. And then the PCH model of the Hexverter is built. On this basis, the IDA-PB controller is designed by solving modulation variables and configuring the interconnection matrix as well as the dam** matrix. Considering that the interference of system parameters may lead to steady-state error, integrators are added to the IDA-PB controller to improve the performance without losing its global asymptotical stability. The voltage-balancing control is applied in order to balance the capacitor DC voltages. The simulation results and experimental results verify that the IDA-PB controller has good regulating ability and strong robustness.