SpringerLink
Log in

Gegenbauer wavelet operational matrix method for solving variable-order non-linear reaction–diffusion and Galilei invariant advection–diffusion equations

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

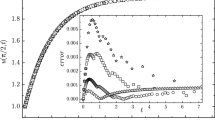
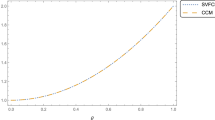
In this article, a variable-order operational matrix of Gegenbauer wavelet method based on Gegenbauer wavelet is applied to solve a space–time fractional variable-order non-linear reaction–diffusion equation and non-linear Galilei invariant advection diffusion equation for different particular cases. Operational matrices for integer-order differentiation and variable-order differentiation have been derived. Applying collocation method and using the said matrices, fractional-order non-linear partial differential equation is reduced to a system of non-linear algebraic equations, which have been solved using Newton iteration method. The salient feature of the article is the stability analysis of the proposed method. The efficiency, accuracy and reliability of the proposed method have been validated through a comparison between the numerical results of six illustrative examples with their existing analytical results obtained from literature. The beauty of the article is the physical interpretation of the numerical solution of the concerned variable-order reaction–diffusion equation for different particular cases to show the effect of reaction term on the pollution concentration profile.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Thailand)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  • Abd-Elkawy MA, Alqahtani RT (2017) Space-time spectral collocation algorithm for the variable-order galilei invariant advection diffusion equations with a nonlinear source term. Math Model Anal 22(1):1–20

    Article  MathSciNet  Google Scholar 

  • Anh VV, Angulo JM, Ruiz-Medina MD (2005) Diffusion on multifractals. Nonlinear Anal Theory Methods Appl 63(5–7):e2043–e2056

    Article  MATH  Google Scholar 

  • Chechkin AV, Gorenflo R, Sokolov IM (2005) Fractional diffusion in inhomogeneous media. J Phys A Math Gen 38(42):L679

    Article  MathSciNet  MATH  Google Scholar 

  • Chechkin A, Gonchar VY, Gorenflo R, Korabel N, Sokolov I (2008) Generalized fractional diffusion equations for accelerating subdiffusion and truncated lévy flights. Phys Rev E 78(2):021111

    Article  MathSciNet  Google Scholar 

  • Coimbra CF (2003) Mechanics with variable-order differential operators. Ann Phys 12(11–12):692–703

    Article  MathSciNet  MATH  Google Scholar 

  • Couteron P, Lejeune O (2001) Periodic spotted patterns in semi-arid vegetation explained by a propagation-inhibition model. J Ecol 89(4):616–628

    Article  Google Scholar 

  • Dabiri A, Moghaddam BP, Machado JT (2018) Optimal variable-order fractional pid controllers for dynamical systems. J Comput Appl Math 339:40–48

    Article  MathSciNet  MATH  Google Scholar 

  • Darania P, Ebadian A (2007) A method for the numerical solution of the integro-differential equations. Appl Math Comput 188:657–668

    MathSciNet  MATH  Google Scholar 

  • Das S, Singh A, Ong SH (2018) Numerical solution of fractional order advection-reaction-diffusion equation. Therm Sci 22:S309–S316

    Article  Google Scholar 

  • Das S, Vishal K, Gupta P (2011) Solution of the nonlinear fractional diffusion equation with absorbent term and external force. Appl Math Model 35(8):3970–3979

    Article  MathSciNet  MATH  Google Scholar 

  • De Villiers J (2012) Mathematics of approximation, vol 1. Springer Science and Business Media, New York

    Book  MATH  Google Scholar 

  • Diethelm K, Ford NJ, Freed AD (2002) A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn 29(1–4):3–22

    Article  MathSciNet  MATH  Google Scholar 

  • Elgindy KT, Smith-Miles KA (2013) Solving boundary value problems, integral, and integro-differential equations using Gegenbauer integration matrices. J Comput Appl Math 237(1):307–325

    Article  MathSciNet  MATH  Google Scholar 

  • Gasca M, Sauer T (2001) On the history of multivariate polynomial interpolation. In: Numerical analysis: historical developments in the 20th century. Elsevier, pp 135–147

  • Gürbüz B, Sezer M (2016) Laguerre polynomial solutions of a class of initial and boundary value problems arising in science and engineering fields. Acta Phys Pol A 130(1):194–197

    Article  Google Scholar 

  • Hajipour M, Jajarmi A, Baleanu D, Sun H (2019) On an accurate discretization of a variable-order fractional reaction-diffusion equation. Commun Nonlinear Sci Numer Simul 69:119–133

    Article  MathSciNet  Google Scholar 

  • Hashim I, Abdulaziz O, Momani S (2009) Homotopy analysis method for fractional IVPS. Commun Nonlinear Sci Numer Simul 14(3):674–684

    Article  MathSciNet  MATH  Google Scholar 

  • Jafari H, Yousefi S, Firoozjaee M, Momani S, Khalique CM (2011) Application of legendre wavelets for solving fractional differential equations. Comput Math Appl 62(3):1038–1045

    Article  MathSciNet  MATH  Google Scholar 

  • Jaiswal S, Chopra M, Das S (2018) Numerical solution of two-dimensional solute transport system using operational matrices. Transp Porous Media 122(1):1–23

    Article  MathSciNet  Google Scholar 

  • Keshi FK, Moghaddam BP, Aghili A (2018) A numerical approach for solving a class of variable-order fractional functional integral equations. Comput Appl Math 37(4):4821–4834

    Article  MathSciNet  MATH  Google Scholar 

  • Kilbas A, Srivastava H, Trujillo JJ (2006) Theory and applications of the fractional differential equations, vol 204. Elsevier (North-Holland), Amsterdam

    MATH  Google Scholar 

  • Kondo S (2009) How animals get their skin patterns: fish pigment pattern as a live turing wave. In: Systems biology. Springer, Berlin, pp 37–46

  • Kondo S, Asai R (1995) A reaction-diffusion wave on the skin of the marine angelfish pomacanthus. Nature 376(6543):765

    Article  Google Scholar 

  • Li Y, Sun N (2011) Numerical solution of fractional differential equations using the generalized block pulse operational matrix. Comput Math Appl 62(3):1046–1054

    Article  MathSciNet  MATH  Google Scholar 

  • Li X, Wu B (2018) Iterative reproducing kernel method for nonlinear variable-order space fractional diffusion equations. Int J Comput Math 95(6–7):1210–1221

    Article  MathSciNet  Google Scholar 

  • Li Y, Zhao W (2010) Haar wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations. Appl Math Comput 216(8):2276–2285

    MathSciNet  MATH  Google Scholar 

  • Lin R, Liu F, Anh V, Turner I (2009) Stability and convergence of a new explicit finite-difference approximation for the variable-order nonlinear fractional diffusion equation. Appl Math Comput 212(2):435–445

    MathSciNet  MATH  Google Scholar 

  • Lv C, Xu C (2016) Error analysis of a high order method for time-fractional diffusion equations. SIAM J Sci Comput 38(5):A2699–A2724

    Article  MathSciNet  MATH  Google Scholar 

  • Machado JT, Kiryakova V, Mainardi F (2011) Recent history of fractional calculus. Commun Nonlinear Sci Numer Simul 16(3):1140–1153

    Article  MathSciNet  MATH  Google Scholar 

  • Machado JAT, Moghaddam BP (2018) A robust algorithm for nonlinear variable-order fractional control systems with delay. Int J Nonlinear Sci Numer Simul 19(3–4):231–238

    Article  Google Scholar 

  • Malesza W, Macias M, Sierociuk D (2019) Analytical solution of fractional variable order differential equations. J Comput Appl Math 348:214–236

    Article  MathSciNet  MATH  Google Scholar 

  • Milici C, Draganescu G, Machado JT (2019) Introduction to fractional differential equations. Nonlinear systems and complexity. Springer, Switzerland. https://doi.org/10.1007/978-3-030-00895-6

  • Moghaddam BP, Machado JAT (2017a) A computational approach for the solution of a class of variable-order fractional integro-differential equations with weakly singular kernels. Fract Calculus Appl Anal 20(4):1023–1042

    MathSciNet  MATH  Google Scholar 

  • Moghaddam BP, Machado JAT (2017b) Extended algorithms for approximating variable order fractional derivatives with applications. J Sci Comput 71(3):1351–1374

    Article  MathSciNet  MATH  Google Scholar 

  • Moghaddam BP, Machado JAT (2017c) Sm-algorithms for approximating the variable-order fractional derivative of high order. Fundam Inf 151(1–4):293–311

    Article  MathSciNet  MATH  Google Scholar 

  • Moghaddam BP, Mostaghim ZS (2017) Modified finite difference method for solving fractional delay differential equations. Boletim da Sociedade Paranaense de Matemática 35(2):49–58

    Article  MathSciNet  MATH  Google Scholar 

  • Moghaddam B, Machado J, Behforooz H (2017) An integro quadratic spline approach for a class of variable-order fractional initial value problems. Chaos Solitons Fractals 102:354–360

    Article  MathSciNet  MATH  Google Scholar 

  • Moghaddam B, Dabiri A, Lopes AM, Machado JT (2019) Numerical solution of mixed-type fractional functional differential equations using modified lucas polynomials. Comput Appl Math 38(2):46

    Article  MathSciNet  MATH  Google Scholar 

  • Murray JD (1981) A pre-pattern formation mechanism for animal coat markings. J Theor Biol 88(1):161–199

    Article  MathSciNet  Google Scholar 

  • Odibat Z (2011) On legendre polynomial approximation with the vim or ham for numerical treatment of nonlinear fractional differential equations. J Comput Appl Math 235(9):2956–2968

    Article  MathSciNet  MATH  Google Scholar 

  • Ortigueira MD, Valério D, Machado JT (2019) Variable order fractional systems. Commun Nonlinear Sci Numer Simul 71:231–243. https://doi.org/10.1016/j.cnsns.2018.12.003. http://www.sciencedirect.com/science/article/pii/S1007570418303782

  • Podlubny I (1998) Fractional differential equations, to methods of their solution and some of their applications. Fractional differential equations: an introduction to fractional derivatives. Academic Press, San Diego

  • Rehman MU, Saeed U (2015) Gegenbauer wavelets operational matrix method for fractional differential equations. J Korean Math Soc 52:1069–1096

    Article  MathSciNet  MATH  Google Scholar 

  • Samko SG, Ross B (1993) Integration and differentiation to a variable fractional order. Integr Transforms Spec Funct 1(4):277–300

    Article  MathSciNet  MATH  Google Scholar 

  • Shen S, Liu F, Chen J, Turner I, Anh V (2012) Numerical techniques for the variable order time fractional diffusion equation. Appl Math Comput 218(22):10861–10870

    MathSciNet  MATH  Google Scholar 

  • Soon CM, Coimbra CF, Kobayashi MH (2005) The variable viscoelasticity oscillator. Ann Phys 14(6):378–389

    Article  MATH  Google Scholar 

  • Suarez L, Shokooh A (1997) An eigenvector expansion method for the solution of motion containing fractional derivatives. ASME J Appl Mech 64:629–635

    Article  MathSciNet  MATH  Google Scholar 

  • Sun H, Chen W, Wei H, Chen Y (2011) A comparative study of constant-order and variable-order fractional models in characterizing memory property of systems. Eur Phys J Spec Top 193(1):185

    Article  Google Scholar 

  • Tavares D, Almeida R, Torres DF (2016) Caputo derivatives of fractional variable order: numerical approximations. Commun Nonlinear Sci Numer Simul 35:69–87

    Article  MathSciNet  Google Scholar 

  • Tripathi NK, Das S, Ong SH, Jafari H, Al Qurashi M (2016) Solution of higher order nonlinear time-fractional reaction diffusion equation. Entropy 18(9):329

    Article  Google Scholar 

  • Valério D, Sá da CJ (2013) Variable order fractional controllers. Asian J Control 15(3):648–657

    Article  MathSciNet  MATH  Google Scholar 

  • **ang M, Zhang B, Yang D (2019) Multiplicity results for variable-order fractional Laplacian equations with variable growth. Nonlinear Anal 178:190–204

    Article  MathSciNet  MATH  Google Scholar 

  • Yuanlu L (2010) Solving a nonlinear fractional differential equation using Chebyshev wavelets. Commun Nonlinear Sci Numer Simul 15(9):2284–2292

    Article  MathSciNet  MATH  Google Scholar 

  • Zayernouri M, Karniadakis GE (2015) Fractional spectral collocation methods for linear and nonlinear variable order FPDES. J Comput Phys 293:312–338

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are thankful to the revered reviewers for their valuable suggestions toward the improvement of the quality of the present article.

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, Indian Institute of Technology (B.H.U), Varanasi, 221005, India

    Sachin Kumar, Prashant Pandey & Subir Das

Authors
  1. Sachin Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Prashant Pandey
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Subir Das
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sachin Kumar.

Additional information

Communicated by José Tenreiro Machado.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, S., Pandey, P. & Das, S. Gegenbauer wavelet operational matrix method for solving variable-order non-linear reaction–diffusion and Galilei invariant advection–diffusion equations. Comp. Appl. Math. 38, 162 (2019). https://doi.org/10.1007/s40314-019-0952-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-019-0952-z

Keywords

Mathematics Subject Classification

Search

Navigation