1 Introduction

The Draper Semi-analytic Satellite Theory (DSST) orbit propagator can be found in two forms, as an option within the Massachusetts Institute of Technology version of the Goddard Trajectory Determination System (GTDS) computer program [1, 2], and as the DSST Standalone orbit propagator package [3,4,5,6,7].

The original implementations of the DSST, both in GTDS and in the Standalone versions, were done in Fortran 77 (F77). Between 2012 and 2015, the DSST was re-implemented in Java and included in the Orekit flight dynamics library [5, 6]. During the same time frame, the University of La Rioja provided web access to the F77 DSST Standalone via a friendly and intuitive interface [8]. In 2016, Setty [7] extended the F77-DSST-Standalone force models, state-transition matrix, and dynamic-parameter partial derivatives to provide the F77-DSST Standalone with orbit determination capability. More recently, the migration of the F77-DSST Standalone code to C/C++ has been done at the University of La Rioja [9, 10].

The theory underlying DSST makes use of the non-singular equinoctial elements and is based on the generalized method of averaging [11,12,13]. The Lagrange Planetary equations are used for handling the conservative terms, \(50\times 50\) gravity fields (M-daily, tesseral resonance and approximate solution of the second-order effect in \(J_2\), \(J_2^2\), based on eccentricity expansions), lunar-solar point masses, and the solid Earth tides, whereas the Gauss equations are used for the atmospheric drag and the solar radiation pressure (SRP).

In particular, the \(J_2^2\) effect was formulated by Zeis [14] in DSST. This author developed an approximate second-order solution as a power series of the eccentricity in \(J_2\) for mean-element and short-periodic motions. This analytical model was implemented with the help of the computer algebra system, Macsyma. Latter, Fisher [15] described the computational procedure required to obtain the \(J_2^2\) effect in closed form. This author proposed two alternatives methods for completing this effect: first, using numerical quadratures and, second, symbolically expanding and manipulating all the mathematical expressions. Unfortunately, time and computer constraints prevented obtaining the full second-order effect. Recently, Folcik and Cefola [16] ported this code to Maxima, the open-source descendant of Macsyma, to calculate the integrant of the mean element rate expressions. The averaged process was carried out using Gauss-Kronrod numerical quadrature. These authors also performed a detailed numerical comparison between Zeis and their numerical model. Finally, they concluded with the necessity of develo** an analytical closed-form model to replace the numerical quadrature process and, so, improve the speed of evaluating the theory.

To obtain the closed-form averaged equations and the mean-to-osculating transformation, we propose an alternative method to build fully second-order closed-form analytical expressions for the \(J_2^2\) contribution based on the Lie-transform method [17,18,19,20,21] and canonical variables consistent with the DSST orbit propagator. The main difference between the Lie transform method and the generalized method of averaging is regarded more as a matter of the algorithm than the underlying idea. In fact, both methods are connected through an integration constant [22, 23]. It is worth noting that the Lie transform method allows us to obtain the transformations from osculating-to-mean and mean-to-osculating elements simultaneously from the generating function.

The main characteristic observed in the application of the generalized method of averaging in the zonal problem in DSST can be found in the calculation of the zonal harmonic short-periodic generator in DSST [24] to which must be added an integration constant to guarantee that the short-period terms do not contain any long-period terms. The equivalent approach is followed by Kozai [25] using Von Zeipel method [26].

In this work, we present a second-order semi-analytical theory for the \(J_2\) problem to remove the short-period terms from the equations of motion using Hamiltonian formalism, an extension of the Lie-Deprit method [27], which is implemented in MathATESAT [28], and Delaunay variables. The resultant theory is equivalent to the elimination of mean anomaly in Kozai [25]. Then, the equations of motion are expressed in equinoctial elements. After that, the transformed equations of motion are analytically and numerically validated. Finally, the Mathematica expressions are migrated to C and included in DSST C.

2 On the \(J_2\) Problem and its Normalization

Extensive investigations dealing with the \(J_2\) problem, or classically called the main problem of artificial satellite theory, have been done since Brouwer’s work [29]. In this section, we present a semi-analytical theory equivalent to the first canonical transformation described in Kozai [25] using an extension of the Lie-Deprit method.

The \(J_2\) problem is defined as a Kepler problem perturbed by Earths oblateness. The Hamiltonian of this dynamical system can be written in a cartesian coordinate system (\({\mathbf {x}}\), \({\mathbf {X}}\)) as

$$\begin{aligned} {\mathcal {H}} = \frac{1}{2} ({\mathbf {X}} \cdot {\mathbf {X}}) - \frac{\mu }{r} \left[ 1-J_2 \left( \frac{\alpha }{r} \right) ^2 P_2\left( \frac{z}{r}\right) \right] , \end{aligned}$$
(1)

where \(r=\Vert {\mathbf {x}}\Vert = \sqrt{x^2+y^2+z^2}\), \({\mathbf {X}}\) is the satellite velocity, \(\mu\) is the gravitational constant, \(\alpha\) the equatorial radius of the Earth, \(J_{2}\) the oblateness coefficient and \(P_2\) the second-degree Legendre polynomial.

The first step to carry out the analytical transformation consists of expressing the Hamiltonian (1) in terms of Delaunay variables \((\ell ,g,h,L,G,H)\) [30, 31]. This set of canonical action-angle variables can be defined in terms of the orbital elements such as

$$\begin{aligned} \begin{array}{l} \ell =M,\\ g=\omega ,\\ h=\Omega , \\ \end{array} \qquad \qquad \begin{array}{l} L=\sqrt{\mu a}, \\ G=\sqrt{\mu a (1 -e^2)}, \\ H=\sqrt{\mu a (1 -e^2)} \cos i, \end{array} \end{aligned}$$
(2)

where M, \(\omega\), \(\Omega\), a, e, i are the mean anomaly, argument of the perigee, longitude of the ascending node, semi-major axis, eccentricity and inclination, respectively. Then, the transformed Hamiltonian is given by

$$\begin{aligned} {{{\mathcal {H}}}} ={{{\mathcal {H}}}}_0 + \varepsilon {{{\mathcal {H}}}}_1, \end{aligned}$$
(3)

where

$$\begin{aligned} {{{\mathcal {H}}}}_0= & {} -\frac{\mu ^2}{2 L^2}, \end{aligned}$$
(4)
$$\begin{aligned} {{{\mathcal {H}}}}_1= & {} \frac{\mu }{2 r}\left( \frac{\alpha }{r}\right) ^2 (3 s^2 \sin ^2 (f + g) -1). \end{aligned}$$
(5)

where \(\varepsilon =J_2\) is a small parameter, \(s= \sin i\) and f is the true anomaly. To avoid any ambiguity in the notation between Delaunay variable and the equinoctial elements \((a,h,k,p,q,\lambda )\), we use \(\Omega\) instead of h to refer to the argument of the node in Delaunay variables.

Next, we normalize the Hamiltonian (3) by applying the Lie transform \(\varphi : (\ell ,g,h,L,G,H) \rightarrow (\ell ',g',h',L',G',H')\), the so-called Delaunay Normalization [32], using the Extended Lie-Deprit method [27]. This perturbation method is based on transforming the analytic Hamiltonian function

$$\begin{aligned} {{{\mathcal {H}}}} = \sum _{n\ge 0} \frac{\varepsilon ^n}{n!} {{{\mathcal {H}}}}_n \equiv \sum _{n\ge 0} \frac{\varepsilon ^n}{n!} {{{\mathcal {H}}}}_{n0} \end{aligned}$$
(6)

into the new one

$$\begin{aligned} {{{\mathcal {K}}}} = \sum _{n\ge 0} \frac{\varepsilon ^n}{n!} {{{\mathcal {K}}}}_n \equiv \sum _{n\ge 0} \frac{\varepsilon ^n}{n!} {{{\mathcal {H}}}}_{0n} \end{aligned}$$
(7)

which satisfies some specific prerequisites. The double index notation in the Hamiltonian is introduced to simplify the automatization of this algorithm. As well as the Lie-Deprit method [18], the extended method looks for a generating function \({{{\mathcal {W}}}}_n= \sum _{n\ge 0} \frac{\varepsilon ^n}{n!} {{{\mathcal {W}}}}_{n+1}\) of \(\varphi\) so that the terms \({{{\mathcal {H}}}}_n\), \({{{\mathcal {K}}}}_n\) and \({{{\mathcal {W}}}}_n\) verify the partial differential equation, called the Homological Equation,

$$\begin{aligned} {\mathcal {L}}_{{\mathcal {H}}_0}({\mathcal {W}}_{n})+{\mathcal {K}}_{n}= \widetilde{{\mathcal {H}}}_{0\,n} \end{aligned}$$
(8)

where \({{{\mathcal {L}}}}_{{{{\mathcal {H}}}}_0 }\) is the Lie operator associated with \({{{\mathcal {H}}}}_0\), a linear operator given in terms of a Poisson bracket.

The right-hand side of the homological equation, \(\widetilde{{\mathcal {H}}}_{0,n}\), is computed from \({\mathcal {H}} _{n}\), \(({\mathcal {W}}_i)_{1 \le i \le n-1}\) and \(({\mathcal {H}}_{p,q})_{p+q \le n-1}\), where the latter are obtained by means of the recursive formula

$$\begin{aligned} {\mathcal {H}}_{i,j} ={\mathcal {H}}_{i+1,j-1} + \displaystyle \sum _{k=0}^i {i \atopwithdelims ()k} \left\{ {\mathcal {H}}_{i-k,j-1}, {\mathcal {W}}_{k+1}\right\} \end{aligned}$$
(9)

with \(i \ge 0\) and \(j \ge 0\) and \(\{\,,\,\}\) represents the Poisson bracket (for more details, see [18]). On the other hand, \(C_n\) is an arbitrary integration function which can depend on \((\_,g',h',L',G',H')\).

In this case, the Lie operator is defined from the zero order Hamiltonian \({{{\mathcal {H}}}}_0\) as \({{{\mathcal {L}}}}_{{{{\mathcal {H}}}}_0 } = n\,\partial /\partial \ell '\), where \(n = \mu ^2/L'^3\) is the mean motion. On the other hand, the solution of the homological equation is obtained as

$$\begin{aligned} {{{\mathcal {K}}}}_n= & {} \frac{1}{2\pi } \int _0^{2\pi } {\widetilde{{\mathcal {H}}}_{0\,n}} \mathrm {d}\ell ', \end{aligned}$$
(10)
$$\begin{aligned} {{{\mathcal {W}}}}_n= & {} \int (\widetilde{{\mathcal {H}}}_{0\,n}-\mathcal { K}_{n})\mathrm {d}\ell ' + C_n{,} \end{aligned}$$
(11)

where \(C_n\), in accordance with Kozai’s work, is chosen to remove the long-period terms contained in the generating function and is given by

$$\begin{aligned} C_n = \frac{1}{2\pi } \int _0^{2\pi } {{{\mathcal {W}}}}_n \mathrm {d}\ell '. \end{aligned}$$
(12)

This semi-analytical theory inherits the intrinsic singularities of the Delaunay variables for the eccentricity, \(e = 0\), and for the inclination, \(i = 0,\pi\). However, the critical inclination is not a problem in the present theory as DSST because perigee’s motion remains in the equation of motion. In the remainder of this paper, we shall drop the primes on the transformed variables to alleviate the notation.

After this summary, we briefly outline the operations that accomplished the elimination of the short period terms using the extended Lie-Deprit method, which up to first-order reads

$$\begin{aligned} {\mathcal {K}}_{0}= & {} {\mathcal {H}}_{0}, \end{aligned}$$
(13)
$$\begin{aligned} {\mathcal {K}}_{1}= & {} {\mathcal {H}}_{1} - \frac{\mu ^{2}}{L^{3}}\frac{\partial {\mathcal {W}_1}}{\partial \ell }. \end{aligned}$$
(14)

Using Eq. (10), we obtain the first-order transformed Hamiltonian as the average over the fastest angle \(\ell\):

$$\begin{aligned} {\mathcal {K}}_1 = \eta \frac{{\mu }^2}{L^2} \left( \frac{{\alpha }^2{\mu }^2}{G^4}\right) \left( \frac{3}{4} s^2-\frac{1}{2}\right) , \end{aligned}$$
(15)

whereas Eq. (11) provides the first-order term of the generating function:

$$\begin{aligned} {\mathcal {W}}_{1}= & {} \frac{\alpha ^2 \mu ^2}{8 \eta ^3 L^3} \left[ 2 \left( 3 s^2-2\right) \phi +2 e \left( 3 s^2-2\right) \sin f \right. \nonumber \\&\left. -3 s^2 \sin (2 f+2 g) -3 e s^2 \sin (f+2 g) \right. \nonumber \\&\left. -e s^2 \sin (3 f+2 g) -\frac{ (\eta -1) (2 \eta +1) s^2 }{ \eta +1} \sin 2 g\right] , \end{aligned}$$
(16)

where \(\eta =\sqrt{1-e^2}\) and \(\phi =f-l\) is the equation of center. Finally, the arbitrary integration function is chosen to be

$$\begin{aligned} C_1= & {} -\frac{\alpha ^2 \mu ^2 (\eta -1) (2 \eta +1) s^2 }{8 \eta ^3 (\eta +1) L^3} \sin 2 g. \end{aligned}$$
(17)

Following the same process, we have that the second-order homological equation is

$$\begin{aligned} {\mathcal {L}}_{{\mathcal {H}}_0}({\mathcal {W}}_{2})+\mathcal { K}_{2}=\{{\mathcal {H}}_1 + {\mathcal {K}}_1,{\mathcal {W}}_1\} + {\mathcal {H}}_2, \end{aligned}$$
(18)

where in this case \({\mathcal {H}}_2=0\). Using Eq. (10), the second-order transformed Hamiltonian is given as

$$\begin{aligned} {{{\mathcal {K}}}}_2= \eta \frac{{\mu }^2}{L^2} \left( \frac{{\alpha }^2{\mu }^2}{G^4}\right) ^2 \sum _{0\le 2k \le 2} P_{i,2k}(s^2,\eta ) \cos 2kg \end{aligned}$$
(19)

where the coefficients \(P_{i,2k}\)

$$\begin{aligned} P_{2,0}= & {} -\frac{105}{64}s^4+\frac{15}{4} s^2-\frac{15}{8} -\left( \frac{27}{16}s^4-\frac{9}{4} s^2+\frac{3}{4}\right) \eta \\&-\left( \frac{15}{64} s^4+\frac{3}{8} s^2-\frac{3}{8}\right) \eta ^2, \\ P_{2,2}= & {} \left( \frac{45}{32} s^4-\frac{21}{16} s^2\right) ( \eta ^2-1) + \frac{3}{8} s^2 \left( 5 s^2-4\right) \frac{(\eta -1) (2 \eta +1)}{ \eta +1}, \end{aligned}$$

are polynomials in s and \(\eta\). The expression of \({{{\mathcal {W}}}}_2\) is included in the Appendix A where the arbitrary integration function is

$$\begin{aligned} C_2= & {} \frac{\alpha ^4 \mu ^4}{256 \eta ^7 (\eta +1) L^7} \left[ 2 s^2 \left( C_2^1 + C_2^2 s^2\right) \sin 2 g -3 C_2^3 s^4 \sin 4 g\right] , \end{aligned}$$
(20)

where the coefficients \(C_2^i\) are polynomials in \(\eta\) and are given by

$$\begin{aligned} C_2^1= & {} 456 \eta ^4+510 \eta ^3+338 \eta ^2-382 \eta -538,\\ C_2^2= & {} -540 \eta ^4-591 \eta ^3-397 \eta ^2+407 \eta +641, \\ C_2^3= & {} 3 (\eta -1)^2 (3 \eta +7). \end{aligned}$$

The direct and inverse transformations of the Lie transform \(\varphi\) are obtained from the generating functions \({\mathcal {W}}_1\) and \({\mathcal {W}}_2\) using the classical recurrent algorithms [18,19,20]. It is worth noting that both transformations expressed in Delaunay variables suffer from the inclusion of the eccentricity in the denominator. Their explicit expressions are not provided here due to a large number of terms.

Finally, Hamilton’s equations, the partial derivatives of the Hamiltonian (19) with respect to the new variables, provide the equations of motion as

$$\begin{aligned} {\displaystyle \frac{\mathrm {d} \ell }{\mathrm {d} t}}= & {} {\displaystyle \frac{\partial {{{\mathcal {K}}}}}{\partial L}} = {\displaystyle \frac{\mu ^2}{L^3}} + \varepsilon \Delta ^{\ell }_1 + {\displaystyle \frac{\varepsilon ^2}{2}}\Delta ^{\ell }_2,\nonumber \\ {\displaystyle \frac{\mathrm {d} g}{\mathrm {d} t}}= & {} {\displaystyle \frac{\partial {{{\mathcal {K}}}}}{\partial G}} = \varepsilon \Delta ^{g}_1 + {\displaystyle \frac{\varepsilon ^2}{2}}\Delta ^{g}_2,\nonumber \\ {\displaystyle \frac{\mathrm {d} \Omega }{\mathrm {d} t}}= & {} {\displaystyle \frac{\partial {{{\mathcal {K}}}}}{\partial H}} = \varepsilon \Delta ^{\Omega }_1 + {\displaystyle \frac{\varepsilon ^2}{2}}\Delta ^{\Omega }_2,\nonumber \\ {\displaystyle \frac{\mathrm {d} L}{\mathrm {d} t}}= & {} -{\displaystyle \frac{\partial {{{\mathcal {K}}}}}{\partial \ell }} = 0,\nonumber \\ {\displaystyle \frac{\mathrm {d} G}{\mathrm {d} t}}= & {} -{\displaystyle \frac{\partial \mathcal{K}}{\partial g}} = {\displaystyle \frac{\varepsilon ^2}{2}} \Delta ^{G}_2, \nonumber \\ {\displaystyle \frac{\mathrm {d} H}{\mathrm {d} t}}= & {} -{\displaystyle \frac{\partial \mathcal{K}}{\partial h}} = 0. \end{aligned}$$
(21)

The first-order coefficients \(\Delta _1^{\ell ,g,\Omega }\) are expressed by

$$\begin{aligned} \Delta ^{\ell }_1= & {} -\frac{3}{4} \frac{{\mu }^2}{L^3 }\left( \frac{{\alpha }^2{\mu }^2}{G^4}\right) (3s^2-2) \eta ,\nonumber \\ \Delta ^{g}_1= & {} -\frac{3}{4} \frac{{\mu }^2}{L^3 }\left( \frac{{\alpha }^2{\mu }^2}{G^4}\right) (5s^2-4),\nonumber \\ \Delta ^{\Omega }_1= & {} -\frac{3}{4} \frac{{\mu }^2}{L^3 }\left( \frac{{\alpha }^2{\mu }^2}{G^4}\right) c, \end{aligned}$$
(22)

where c represents the cosine of the inclination. On the other hand, the second-order coefficients \(\Delta _2^{\ell ,g,\Omega ,G}\) are

$$\begin{aligned} \Delta ^{\ell }_2= & {} \frac{3}{64} \frac{{\mu }^2}{L^3 }\left( \frac{{\alpha }^2{\mu }^2}{G^4}\right) ^2 \eta \left[ {\bar{P}}_{2,0}^{\ell } - \frac{2}{(\eta +1)^2}{\bar{P}}_{2,2}^{\ell } \cos 2g\right] ,\nonumber \\ \Delta ^{g}_2= & {} \frac{3}{64} \frac{{\mu }^2}{L^3 }\left( \frac{{\alpha }^2{\mu }^2}{G^4}\right) ^2 \ \left[ {\bar{P}}_{2,0}^{g} - \frac{2}{(\eta +1)^2}{\bar{P}}_{2,2}^{g}\cos 2g\right] ,\nonumber \\ \Delta ^{\Omega }_2= & {} \frac{3}{16} \frac{{\mu }^2}{L^3 }\left( \frac{{\alpha }^2{\mu }^2}{G^4}\right) ^2 \ c \left[ {\bar{P}}_{2,0}^{\Omega } - \frac{2(\eta -1)}{\eta +1}{\bar{P}}_{2,2}^{\Omega } \cos 2g\right] ,\nonumber \\ \Delta ^{G}_2= & {} \frac{3}{16} \frac{{\mu }^2}{L^3 }\left( \frac{{\alpha }^2{\mu }^2}{G^4}\right) ^2 \frac{\eta (\eta -1)}{\eta +1} s^2 {\bar{P}}_{2,2}^{G} \sin 2g, \end{aligned}$$
(23)

where the polynomials \({\bar{P}}_{2,i}^{\ell ,g,\Omega ,G}\) depend on \(s^2\), \(\eta\) and are given by

$$\begin{aligned} {\bar{P}}_{2,0}^{\ell }= & {} 5 \left( 5 s^4+8 s^2-8\right) \eta ^2 + 16 \left( 2-3 s^2\right) ^2 \eta + 15 \left( 7 s^4-16 s^2+8\right) ,\nonumber \\ {\bar{P}}_{2,2}^{\ell }= & {} 5 s^2 \left( 15 s^2-7\right) \eta ^4 +2 s^2 \left( 155 s^2-67\right) \eta ^3 +10 s^2 \left( 17 s^2-7\right) \eta ^2 \nonumber \\&+30 s^2 \left( 3-7 s^2\right) \eta +15 s^2 \left( 3-7 s^2\right) ,\nonumber \\ {\bar{P}}_{2,0}^{g}= & {} \left( 45 s^4+36 s^2-56\right) \eta ^2 +24 \left( 15 s^4-22 s^2+8\right) \eta \nonumber \\&+5 \left( 77 s^4-172 s^2+88\right) ,\nonumber \\ {\bar{P}}_{2,2}^{g}= & {} \left( 135 s^4-158 s^2+28\right) \eta ^4 + \left( 670 s^4-732 s^2+120\right) \eta ^3 \nonumber \\&+2 \left( 55 s^4 -66 s^2+16\right) \eta ^2 -10 \left( 77 s^4-82 s^2+12\right) \eta \nonumber \\&-5 \left( 77 s^4-82 s^2+12\right) ,\nonumber \\ {\bar{P}}_{2,0}^{\Omega }= & {} \left( 5 s^2+4\right) \eta ^2 + \left( 36 s^2-24\right) \eta +5 \left( 7 s^2-8\right) ,\nonumber \\ {\bar{P}}_{2,2}^{\Omega }= & {} \left( 15 s^2-7\right) \eta ^2 + \left( 70 s^2-30\right) \eta +5 \left( 7 s^2-3\right) ,\nonumber \\ {\bar{P}}_{2,2}^{G}= & {} \left( 15 s^2-14\right) \eta ^2+ \left( 70 s^2-60\right) \eta +5 \left( 7 s^2-6\right) . \end{aligned}$$
(24)

In order to include this theory in DSST, the transformations and equations of motion are formed in terms of the non-singular equinoctial element set.

3 Mean Equinoctial Variational Equations

In this section, we derive the mean equinoctial variational equations from Hamilton’s equations (21). The equinoctial elements [33] are defined in terms of the orbital elements as follows:

$$\begin{aligned} \begin{array}{l} a = a,\\ h = e \sin (\omega + \mathrm {I} \Omega ),\\ k = e \cos (\omega + \mathrm {I} \Omega ), \\ \end{array} \qquad \qquad \begin{array}{l} p = \tan ^\mathrm {I}\left( i/2\right) \sin \Omega , \\ q = \tan ^\mathrm {I}\left( i/2\right) \cos \Omega , \\ \lambda = M + \omega + \mathrm {I} \Omega , \end{array} \end{aligned}$$
(25)

where \(\mathrm {I}\) is called the retrograde factor. The factor \(\mathrm {I}\) takes the value 1 for the direct equinoctial elements and -1 for the retrograde equinoctial elements, although direct orbits can include the range of inclination \([0,\pi )\).

To derive the equinoctial equation of motion, we start by differentiating Eq. (25) with respect to time, the derivatives of the equinoctial elements can be written in terms of the orbital elements and their derivatives:

$$\begin{aligned} \frac{\mathrm {d} a}{\mathrm {d} t}= & {} \frac{\mathrm {d} a}{\mathrm {d} t}, \nonumber \\ \frac{\mathrm {d} h}{\mathrm {d} t}= & {} \frac{h}{e} \frac{\mathrm {d} e}{\mathrm {d} t} + k \left( \frac{\mathrm {d} \omega }{\mathrm {d} t} + \mathrm {I} \frac{\mathrm {d} \Omega }{\mathrm {d} t} \right) , \nonumber \\ \frac{\mathrm {d} k}{\mathrm {d} t}= & {} \frac{k}{e} \frac{\mathrm {d} e}{\mathrm {d} t} - h \left( \frac{\mathrm {d} \omega }{\mathrm {d} t} + \mathrm {I} \frac{\mathrm {d} \Omega }{\mathrm {d} t} \right) , \nonumber \\ \frac{\mathrm {d} p}{\mathrm {d} t}= & {} \frac{1}{2} \mathrm {I} \sec ^2\left( i/2\right) \tan ^\mathrm {I-1}\left( i/2\right) \sin \Omega \frac{\mathrm {d} i}{\mathrm {d} t} + q \frac{\mathrm {d} \Omega }{\mathrm {d} t}, \nonumber \\ \frac{\mathrm {d} q}{\mathrm {d} t}= & {} \frac{1}{2} \mathrm {I} \sec ^2\left( i/2\right) \tan ^\mathrm {I-1}\left( i/2\right) \cos \Omega \frac{\mathrm {d} i}{\mathrm {d} t} - p \frac{\mathrm {d} \Omega }{\mathrm {d} t}, \nonumber \\ \frac{\mathrm {d}\lambda }{\mathrm {d} t}= & {} \frac{\mathrm {d} M}{\mathrm {d} t} + \frac{\mathrm {d} \omega }{\mathrm {d} t} + \mathrm {I} \frac{\mathrm {d} \Omega }{\mathrm {d} t}. \end{aligned}$$
(26)

The derivatives on the right-hand sides of Eq. (26) are obtained in a straightforward manner by differentiating Eq. (2) with respect to time as

$$\begin{aligned} {\displaystyle \frac{\mathrm {d} a}{\mathrm {d} t}}= & {} {\displaystyle \frac{2 L }{\mu }} {\displaystyle \frac{\mathrm {d} L}{\mathrm {d} t}},\nonumber \\ {\displaystyle \frac{\mathrm {d} e}{\mathrm {d} t}}= & {} {\displaystyle \frac{1}{e L}} \left( (1-e^2) {\displaystyle \frac{\mathrm {d} L}{\mathrm {d} t}} - \sqrt{1-e^2} {\displaystyle \frac{\mathrm {d} G}{\mathrm {d} t}}\right) ,\nonumber \\ {\displaystyle \frac{\mathrm {d} i}{\mathrm {d} t}}= & {} {\displaystyle \frac{1}{G \sin i}} \left( \cos i {\displaystyle \frac{\mathrm {d} G}{\mathrm {d} t}} - {\displaystyle \frac{\mathrm {d} H}{\mathrm {d} t}}\right) ,\nonumber \\ {\displaystyle \frac{\mathrm {d} \omega }{\mathrm {d} t}}= & {} {\displaystyle \frac{\mathrm {d} g}{\mathrm {d} t}}, \, {\displaystyle \frac{\mathrm {d} M}{\mathrm {d} t}} = {\displaystyle \frac{\mathrm {d} \ell }{\mathrm {d} t}}. \end{aligned}$$
(27)

Then, considering mean elements in Eqs. (26 and 27) and using Hamilton’s equations Eq. (21), after some complex algebraic manipulation, we obtain the mean equinoctial variational equations as

$$\begin{aligned} {\displaystyle \frac{\mathrm {d} \sigma }{\mathrm {d} t}} = \sum _{k=0}^2 \frac{\varepsilon ^k}{k!}{\bar{\Delta }}_k^{\sigma }, \end{aligned}$$
(28)

where \(\mathrm {d} a/\mathrm {d} t=0\) and \(\sigma\) represents the mean equinoctial elements \((h,k,p,q,\lambda )\). It is worth noting that Eqs. (28) depend on the orbital elements a, e, i and \(\omega\).

Finally, we will obtain Eqs (28) in equinoctial elements taking into account Eqs. (25) and the transformation from the equinoctial elements to the orbital elements given by

$$\begin{aligned} a= & {} a, \nonumber \\ e= & {} \sqrt{h^2+k^2},\nonumber \\ i= & {} \pi \left( \frac{1- \mathrm {I}}{2}\right) + 2 \mathrm {I} \arctan \sqrt{p^2+q^2},\nonumber \\ \sin \Omega= & {} \frac{p}{\sqrt{p^2+q^2}}, \nonumber \\ \cos \Omega= & {} \frac{q}{\sqrt{p^2+q^2}} ,\nonumber \\ \omega= & {} \zeta - \mathrm {I} \Omega , \nonumber \\ M= & {} \lambda - \zeta , \end{aligned}$$
(29)

where \(\zeta\) is an auxiliary angle, which is defined by:

$$\begin{aligned} \sin \zeta= & {} \frac{h}{\sqrt{h^2+k^2}},\nonumber \\ \cos \zeta= & {} \frac{k}{\sqrt{h^2+k^2}}. \end{aligned}$$
(30)

The zero-order terms in equinoctial elements are \({\bar{\Delta }}_0^{h}={\bar{\Delta }}_0^{k}={\bar{\Delta }}_0^{p}={\bar{\Delta }}_0^{q}=0\) and \({\bar{\Delta }}_0^{\lambda }=n\) where \(n=\sqrt{\mu /a^3}\) is the mean motion. The first-order terms only depend on the momenta L, G and \(\eta\), s, c allowing us to obtain the \(\Delta _1^{\sigma }\) terms in a straightforward manner as

$$\begin{aligned} \Delta _1^{h}= & {} -{{{\mathcal {C}}}}_1 k \chi ,\nonumber \\ \Delta _1^{k}= & {} {{{\mathcal {C}}}}_1 h \chi ,\nonumber \\ \Delta _1^{p}= & {} -2 {{{\mathcal {C}}}}_1 c q,\nonumber \\ \Delta _1^{q}= & {} 2 {{{\mathcal {C}}}}_1 c p,\nonumber \\ \Delta _1^{\lambda }= & {} -{{{\mathcal {C}}}}_1 \left[ (3 \eta +5) s^2+ 2 \mathrm {I} c -2 (\eta +2)\right] , \end{aligned}$$
(31)

where \({{{\mathcal {C}}}}_1=3 \alpha ^2 n/(4 a^2 \eta ^4)\) and \(\chi = 5 s^2 + 2 \mathrm {I} c - 4\). The expressions of \(\eta\), c and s in equinoctial elements are

$$\begin{aligned} \eta = \sqrt{1-h^2-k^2}, \quad c = \frac{1-p^2-q^2}{1+p^2+q^2},\quad s = \frac{2 \sqrt{p^2+q^2}}{1+p^2+q^2}.\end{aligned}$$

As it can be seen, Eq. (31) are valid for both direct and retrograde equinoctial elements and agree with known results [14, 34].

The expressions of the second-order terms to equinoctial elements are not directly calculated, The second-order Hamilton equations introduce the contribution of the argument of the perigee g through terms in \(\sin 2g\) and \(\cos 2g\). Using Eq. (25), these trigonometric functions are converted to equinoctial elements and yield

$$\begin{aligned} \sin 2g= & {} \frac{2 (h q - \mathrm {I} k p) (\mathrm {I} h p+k q)}{(h^2+k^2)(p^2+q^2)},\nonumber \\ \cos 2g= & {} \frac{ \left( h^2-k^2\right) \left( p^2-q^2\right) +4 \mathrm {I} h k p q }{(h^2+k^2)(p^2+q^2)}. \end{aligned}$$
(32)

After a laborious simplification process, we obtained that the \(\Delta _2^{\sigma }\) terms were not entirely non-singular. These terms depended on the factor \((p^2 + q^2)^{-2 I}\). Therefore, it was not possible to derive a unique set of expressions valid for both direct and retrograde orbits.

For the case of direct orbits \((I=1)\) and the range of inclination \([0,\pi )\), we obtain the following non-singular expressions

$$\begin{aligned} \Delta ^{h}_2= & {} {{{\mathcal {C}}}}_2\sum _{m_1=0}^1\sum _{m_2=0}^3 \sum _{m_3=0}^8\sum _{m_4=0}^8 \mathrm {P}^{(m_1,m_2,m_3,m_4)}_{h} h^{m_1} k^{m_2} p^{m_3} q^{m_4},\nonumber \\ \Delta ^{k}_2= & {} {{{\mathcal {C}}}}_2 \sum _{m_1=0}^3\sum _{m_2=0}^1 \sum _{m_3=0}^8\sum _{m_4=0}^8 \mathrm {P}^{(m_1,m_2,m_3,m_4)}_{k} h^{m_1} k^{m_2} p^{m_3} q^{m_4},\nonumber \\ \Delta ^{p}_2= & {} {{{\mathcal {C}}}}_2^* \sum _{m_1=0}^2\sum _{m_2=0}^2 \sum _{m_3=0}^8\sum _{m_4=0}^9 \mathrm {P}^{(m_1,m_2,m_3,m_4)}_{p} h^{m_1} k^{m_2} p^{m_3} q^{m_4},\nonumber \\ \Delta ^{q}_2= & {} {{{\mathcal {C}}}}_2^* \sum _{m_1=0}^2\sum _{m_2=0}^2 \sum _{m_3=0}^9\sum _{m_4=0}^8 \mathrm {P}^{(m_1,m_2,m_3,m_4)}_{q} h^{m_1} k^{m_2} p^{m_3} q^{m_4},\nonumber \\ \Delta ^{\lambda }_2= & {} {{{\mathcal {C}}}}_2 \sum _{m_1=0}^2\sum _{m_2=0}^2 \sum _{m_3=0}^8\sum _{m_4=0}^8 \mathrm {P}^{(m_1,m_2,m_3,m_4)}_{\lambda } h^{m_1} k^{m_2} p^{m_3} q^{m_4}, \end{aligned}$$
(33)

where

$$\begin{aligned} {{{\mathcal {C}}}}_2= & {} \frac{3 \alpha ^4 n}{8 a^4 \eta ^8 (\eta +1)^3 \left( p^2+q^2+1\right) ^4},\nonumber \\ {{{\mathcal {C}}}}_2^*= & {} \frac{3 \alpha ^4 n \left( p^2+q^2-1\right) }{8 a^4 \eta ^8 (\eta +1)^2 \left( p^2+q^2+1\right) ^3}, \end{aligned}$$
(34)

and the coefficients \(\mathrm {P}^{(m_1,m_2,m_3,m_4)}_{\sigma }\) are polynomial in \(\eta\). The values of these coefficients are given in Tables 2–7 of the Appendix B.

For the case of retrograde orbits \((I=-1)\) and \(i=\pi\), we have that \(p=q=0\) and take the limits when \(p\rightarrow 0\) and \(q\rightarrow 0\) and we obtain

$$\begin{aligned} \Delta ^{h}_2= & {} {{{\mathcal {C}}}}_2 k [ q_3(\eta ) + 4 q_2(\eta ) h^2 ],\nonumber \\ \Delta ^{k}_2= & {} {{{\mathcal {C}}}}_2 h [ q_5(\eta ) + 4 q_2(\eta )k^2],\nonumber \\ \Delta ^{p}_2= & {} 0,\nonumber \\ \Delta ^{q}_2= & {} 0,\nonumber \\ \Delta ^{\lambda }_2= & {} - {{{\mathcal {C}}}}_2 [q_1(\eta ) q_4(\eta ) + 4 q_2(\eta )k^2], \end{aligned}$$
(35)

where

$$\begin{aligned} {{{\mathcal {C}}}}_2=\frac{3 \alpha ^4 n}{8 a^4 \eta ^8 (\eta +1)^2}, \end{aligned}$$

and the coefficient \(q_i(\eta )\) is a polynomial in \(\eta\) of \(i\mathrm {th}\) order with the coefficients in Table 1.

Table 1 Value of the polynomials \(q_i(\eta )\)
Full size table

Finally, the second-order terms have been tested reproducing the solution provided by Zeis [14]. This approach has been derived from the beginning considering the first-order approximation in the eccentricity of the transformed Hamiltonian \({\mathcal {K}}_2\) (19) which yields

$$\begin{aligned} {\mathcal {K}}_2^{\mathrm {Zeis}} = -\frac{3 \alpha ^4 \mu ^6 \left( 19 s^4-30 s^2+12\right) }{16 L^{10}}+{\mathcal {O}}\left( e^2\right) . \end{aligned}$$
(36)

Following the same process used to build the \(\Delta _2^{\sigma }\) terms (33), the corresponding second-order terms in the Zeis case are

$$\begin{aligned} \Delta ^{h}_2= & {} {{{\mathcal {C}}}}_2^Z k\left( 19 s^2-15\right) \left( s^2 + \mathrm {I}c-1\right) ,\nonumber \\ \Delta ^{k}_2= & {} - {{{\mathcal {C}}}}_2^Z h \left( 19 s^2-15\right) \left( s^2 + \mathrm {I}c-1\right) ,\nonumber \\ \Delta ^{p}_2= & {} {{{\mathcal {C}}}}_2^Z c q \left( 19 s^2-15\right) ,\nonumber \\ \Delta ^{q}_2= & {} - {{{\mathcal {C}}}}_2^Z c p \left( 19 s^2-15\right) ,\nonumber \\ \Delta ^{\lambda }_2= & {} {\displaystyle \frac{{{{\mathcal {C}}}}_2^Z}{2 }} \left[ 2 \left( 19s^2-15\right) \left( s^2+\mathrm {I} c-1\right) +5 \left( 19 s^4-30s^2+12\right) \eta \right] , \end{aligned}$$
(37)

where \({{{\mathcal {C}}}}_2^Z=3 \alpha ^4 n/(4 a^4 \eta )\). In this simplified case, the expressions do not include any singularity and are valid for both direct and retrograde orbits and agree with known results [14, 34].

4 Numerical Experiments

Validation of any analytical or semi-analytical theories is not a trivial task since the accuracy of the theory mainly depends on its correct initialization [35, 36]. In the semi-analytical theory presented in this paper, the osculating-to-mean and mean-to-osculating transformations are expressed in the singular Delaunay variables, which introduce an additional problem to its validation. Both issues do not allow us to reproduce or reach the accuracy of the results presented in Fig. 6 in the work of Folcik and Cefola [16]. These authors use orbital determination techniques to adjust the initial conditions properly, whereas the mean-to-oscillating transform is formulated in the non-singular equinoctial variables.

Finally, we compared the first-order, the truncate second-order (Zeis’s solution), and the closed-form second-order semi-analytical theories (SA) with the non-transformed equations of motion for three families of orbits. The first family, low-altitude near circular orbits, has a 200 km perigee height by 210 km apogee, the second 200 km perigee height by 500 km apogee, and the third 200 km perigee height by 1000 km apogee. The inclination varies from zero to 180 degrees. Both transformed and non-transformed equations of motion were integrated using a highly accurate eighth-order Runge-Kutta method [37] (NUM) for two days. Then, their respective outputs, \({\mathbf {x}}_{SA_i}\) and \({\mathbf {x}}_{NUM_i}\), were then compared in terms of their RMS of position differences, as given in Eq. (38).

$$\begin{aligned} {\mathrm {RMS}_{pos} = \sqrt{\frac{1}{n} \sum _{i=1}^n (\Vert {\mathbf {x}}_{NUM_i} -{\mathbf {x}}_{SA_i}\Vert )^2}.} \end{aligned}$$
(38)

The equations of motion are formulated in equinoctial elements, whereas the changes from mean-to-osculating and osculating-to-mean remain in the Delaunay variables.

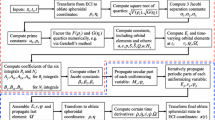
Figure 1 describes the evaluation process of the semi-analytical theories. The initial osculating elements \({\mathbf {x}}_{t_0}\) are transformed to initial mean elements \(\bar{{\mathbf {x}}}_{t_0}\) using the osculating-to-mean transformation. Then, the mean equations of motion are numerically integrated. Finally, the osculating elements \({\mathbf {x}}_{t}\) are obtained through the mean-to-osculating transformation. It is worth noting that the non-transformed equations of motion are integrated starting with the same initial conditions \({\mathbf {x}}_{t_0}\).

Fig. 1
figure 1

Evaluation process of a semi-analytical theory

Full size image

Figure 2 shows the position error RMS between the first-order semi-analytical theory and the numerical integration of the non-transformed problem for the three families of orbits. As can be seen, the errors are symmetric for the 90 degrees of inclination. For the 200\(\times\)210 km family, the maximum error is 10 km, obtained at an inclination of 90 degrees, whereas the minimum is 4.37 km, at an inclination around 52 and 128 degrees. The maximum errors are reduced as the apogee height is increased to 500 km and 1000 km to 2.2 and 2 km for inclinations 0 and 180 degrees, respectively. The minimum errors are approximately 0.47 km at inclinations around 74 and 106 degrees.

Fig. 2
figure 2

Position error RMS for the first-order semi-analytical theory for three families of orbits as the inclination is varied from 0 to 180 degrees. The family in green includes a 200 km perigee height by 210 km apogee height (near circular) orbit, in red 200 km perigee height by 500 km apogee height orbit, and in blue 200 km perigee height by 1000 km apogee height orbit

Full size image

Figure 3 shows the position error RMS for the truncate (blue) and the closed-form (red) second-order semi-analytical theories for the family near-circular orbits (\(e=0.000759\)). The position errors remain the symmetry to the 90 degrees of inclination. As can be seen, the truncate and the closed-form solutions are very close to each other, which is consistent with the small eccentricity case. The difference between both lines is very small. The maximum error of the two theories is around 463 m for the inclinations of 0 and 180 degrees, whereas the minimum error is around 117 m. for the inclinations of 54 and 126 degrees.

Fig. 3
figure 3

Position error RMS for the second-order semi-analytical theory for the family near circular orbits as inclination is varied from 0 to 180 degrees and 200 km perigee height by 210 km apogee height orbit. Red represents closed-form second-order theory and blue the truncate approach

Full size image

Figure 4 depicts the difference between the closed-form and the truncate position errors plotted in Fig. 3. The accuracy provided by the truncate solution is only better between 65 and 180, whereas the closed-form solution is in the rest. We assume that this behaviour mainly lies in the small eccentricity of this family and in conserving the transformations from osculating-to-mean and mean-to-osculating in Delaunay variables.

Fig. 4
figure 4

Difference between the closed-form and truncate position errors plotted in Fig. 3

Full size image

Figure 5 shows the position error RMS for the truncate (dashed line) and the closed-form (continuous line) second-order semi-analytical theories for two families of orbits with 500 km (red) and 1000 km (blue) apogee height, respectively. As can be seen, the position errors are symmetrical to the 90 degrees of inclination. The loss of accuracy produced by conserving the singular Delaunay variables in the transformations is visible in the family with 500 km apogee height as inclination varies from 0 to 50 and 130 to 180 degrees. The maximum errors of both theories are reached for the inclination of 0 and 180 degrees, with around 180 m for the closed-form and 160 m for the truncate. The minimum errors or the closed and truncated theories are around 63 m and 45 m for an inclination of 55 and 45 degrees, respectively. However, this behaviour changes for the family with 1000 km apogee height. The accuracy of the closed-form theory improves the truncate one for all inclination. The maximum and minimum errors in the closed-form are 173 m and 95 m, respectively, whereas in the truncate are 335 m and 131 m.

Fig. 5
figure 5

Position error RMS for the second-order semi-analytical theory for two families of orbits as the inclination is varied from 0 to 180 degrees. The family in red includes the 200 km perigee height by 500 km apogee height orbits, and in blue, the family of 200 km perigee height by 1000 km apogee height orbits. The continuous line indicates the closed-form second-order theory and the dashed line the truncate approach

Full size image

Finally, Fig. 6 simulates the current status of the different implementations of the \(J_2^2\) effect in GTDS-DSST and DSST Standalone using the closed-form and truncate mean equations of motion and the families of 500 km (red) and 1000 km (blue) apogee height. The second-order osculating-to-mean transformation was applied to the initial conditions. On the other hand, the change from mean to osculating is done using the first-order expressions. For both families of orbits, the accuracy of the closed-form equations of motion slightly predominates over the accuracy given by the truncate equations. It is not clear for the family of 500 km because both lines are close to each other, as can be seen in Fig. 7. However, this behaviour can be appreciated in the family of 1000 km apogee height, especially for inclinations from 40 to 130 degrees. It is worth noting that the asymmetry errors at 0 and 180 degrees inclination detected in [16] do not appear in our analytical expressions.

Fig. 6
figure 6

Position error RMS for the second-order semi-analytical theory for two families of orbits as the inclination is varied from 0 to 180 degrees. The family in red includes the 200 km perigee height by 500 km apogee height orbits, and in blue, the family of 200 km perigee height by 1000 km apogee height orbits. The continuous line indicates the closed-form second-order theory and the dashed line the truncate approach. The transformation from mean to osculating and from osculating to mean is done using the first-order expressions

Full size image
Fig. 7
figure 7

Difference between the closed-form and truncate position errors plotted in Fig. 6

Full size image

5 Conclusion and Future Work

In this paper, a second-order closed-form semi-analytical solution of the \(J_2\) problem has been developed. An extension of the Lie-Deprit method and Delaunay variables is used to remove the short-period terms from the equations of motion using the Hamiltonian formalism. This semi-analytical theory has been implemented using MathATESAT a Mathematica-based tool.

The averaged equations of motion are given explicitly and transformed into the non-singular equinoctial elements. This semi-analytical theory is equivalent to others in which Lagrange Planetary equations, as well as General Averaging Method and equinoctial elements, are used, and hence, consistent with the Draper Semi-analytic Satellite Theory. These analytical expressions improve the computational speed of the numerical-based approach, which is only available in the GTDS-DSST version.

Additionally, the second-order terms have been tested reproducing the solution provided by Zeis, validated numerically, and included in DSST C.

Finally, we are currently working on expressing the second-order mean-to-osculating transformation in equinoctial elements, calculating the partial derivatives necessary for an orbit determination system and integrating GTDS-DSST and DSST Standalone. It is worth noting that these expressions are essential to reach the complete accuracy of the second-order theory.