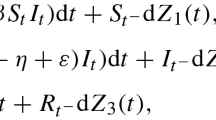Abstract
A stochastic SIR epidemic model taking into account the heterogeneity of the spatial environment is constructed. The deterministic model is given by a partial differential equation and the stochastic one by a space-time jump Markov process. The consistency of the two models is given by a law of large numbers. In this paper, we study the deviation of the spatial stochastic model from the deterministic model by a functional central limit theorem. The limit is a distribution-valued Ornstein–Uhlenbeck Gaussian process, which is the mild solution of a stochastic partial differential equation.
Similar content being viewed by others
References
Bahouri, H., Chemin, J., Danchin, R.: Fourier Analysis and Nonlinear Partial Differential Equations. Springer, Berlin (2011)
Blount, D.J.: Limit theorems for a sequence of nonlinear reaction–diffusion systems. Stoch. Process. Appl. 45(2), 193–207 (1993)
Britton, T., Pardoux, E.: Stochastic Epidemic Models with Inference, Lecture notes in Math. 2255. Springer (2019)
Droniou, J., Eymard, R., Gallouët, T., Herbin, R.: The Gradient Discretisation Method. Springer, New York (2018)
Joffe, A., Metivier, M.: Weak convergence of sequences of semimartingales with applications to multitype branching processes. Adv. Appl. Probab. 18(1), 20–65 (1986)
Kermack, W.O., McKendrick, A.G.: Proc. Roy. Soc. A 115 , 700. Reprinted in Bull. Math. Biol. 53, 33 (1991)
Kotelenez, P.: Gaussian approximation to the nonlinear reaction–diffusion equation. Report 146, Universität Bremen Forschungsschwerpunkt Dynamische Systemes (1986)
Kotelenez, P.: A stopped Doob inequality for stochastic convolution integrals and stochastic evolution equations. Stoch. Anal. Appl. 2(3), 245–265 (1984)
Kurtz, T.G.: Limit theorems for sequences of of jump Markov processes approximating ordinary differential processes. J. Appl. Probab. 8, 344–356 (1971)
N’zi, M., Pardoux, E., Yeo, T.: A SIR model on a refining spatial grid I. Law of large numbers. Appl. Math. Optim. 83, 1153–1189 (2021)
Taylor, M.E.: Partial Differential Equations III Nonlinear Equations. Springer, Berlin (1991)
Acknowledgements
The author Ténan Yeo would like to thank the Marseille Mathematics Institute (I2M) for funding his stay in Marseille, during which part of this work was carried out.
Funding
The authors were supported by their respective university.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest and no competing interests. The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A
Appendix A
Lemma A.1
Let \((h_\varepsilon )_{0<\varepsilon <1}\) be a sequence of \(\texttt{H}_{\varepsilon }\). If \((h_\varepsilon )_{0<\varepsilon <1}\) is bounded in \(\textrm{H}^{1,\varepsilon }\), then it is relatively compact in \(L^2\), and the limit of any convergent subsequence belongs to \(\textrm{H}^{1}\).
Proof
By using the fact that the sequence \((h_\varepsilon )\) is bounded in \(L^2\) and \(\big \Vert \nabla _{\!\!\varepsilon }^+h_\varepsilon \big \Vert _{L^2}\le C\big \Vert h_\varepsilon \big \Vert _{_{\textrm{H}^{1}}}\), then the result of the compactness follows from the compactness theorem of Kolmogorov in \(L^2\).
The fact the limit of any convergent subsequence belong to \(\textrm{H}^{1}\), follows from the discrete integrating by part
and letting \(\varepsilon \) go to zero in this equation. \(\square \)
Lemma A.2
For all \(\displaystyle u_{\varepsilon } \in \texttt{H}_{\varepsilon } \)
\( \displaystyle \big \Vert \nabla _{\!\!\varepsilon }^- u_{\varepsilon }\big \Vert _{_{\textrm{H}^{-\gamma , \varepsilon }}}^2 = \big \Vert \nabla _{\!\!\varepsilon }^+ u_{\varepsilon }\big \Vert _{_{\textrm{H}^{-\gamma , \varepsilon }}}^2= \sum _m \left( \langle \,u_{\varepsilon } , \varphi _{m}^{\varepsilon }\,\rangle ^2 + \langle \,u_{\varepsilon } , \psi _{m}^{\varepsilon }\,\rangle ^2 \right) \lambda _{m}^{\varepsilon }(1+\lambda _{m}^{\varepsilon })^{-\gamma }. \)
Proof
We have
where \(a_{m,\varepsilon }=\varepsilon ^{-1}\sin (\pi m\varepsilon )\) and \(b_{m,\varepsilon }=\varepsilon ^{-1} (\cos (\pi m\varepsilon )-1)\).
We have
Let \(\displaystyle u_{\varepsilon } \in \texttt{H}_{\varepsilon } \). We have
The proof of \(\displaystyle \big \Vert \nabla _{\!\!\varepsilon }^- u_{\varepsilon }\big \Vert _{_{\textrm{H}^{-\gamma , \varepsilon }}}^2 = \sum _m \left( \langle \,u_{\varepsilon } , \varphi _{m}^{\varepsilon }\,\rangle ^2 + \langle \,u_{\varepsilon } , \psi _{m}^{\varepsilon }\,\rangle ^2 \right) \lambda _{m}^{\varepsilon }(1+\lambda _{m}^{\varepsilon })^{-\gamma } \) is similar by noting that
\(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Gallouët, T., Pardoux, É. & Yeo, T. A SIR epidemic model on a refining spatial grid II-central limit theorem. Stoch PDE: Anal Comp (2024). https://doi.org/10.1007/s40072-024-00333-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40072-024-00333-0