SpringerLink
Log in

Oscillatory Free Convective Flow of Viscoelastic Fluid Through Porous Medium in a Rotating Vertical Channel

  • Research Article
  • Published:
Proceedings of the National Academy of Sciences, India Section A: Physical Sciences Aims and scope Submit manuscript

Abstract

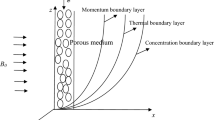
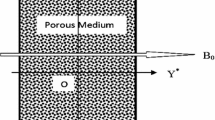
A theoretical analysis of an oscillatory viscoelastic, incompressible and electrically conducting fluid in an infinite vertical porous channel is presented. The entire system rotates about the axis normal to the plane of the plate with uniform angular velocity \( \Upomega \). A closed form solution for the velocity, temperature and skin friction are obtained. Results are presented through graphs and table for the various values of rotation, viscoelastic, permeability and frequency of oscillation parameter and discussed in detail.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Abbreviations

C p :

Specific heat at constant pressure

g:

Acceleration due to gravity

K*:

Permeability of the medium

\( K_{0}^{*} \) :

Viscoelastic parameter

p*:

Modified pressure

t*:

Time

T :

Temperature

(u, v, w):

Fluid velocity along x, y, z-axis

\( \alpha \) :

Modulus of rigidity

\( \beta \) :

Coefficient of volume expansion

\( \epsilon \) :

Small positive constant

\( \kappa \) :

Thermal conductivity

\( \mu \) :

Coefficient of viscosity

\( \nu \) :

Kinematic viscosity

\( \omega \) :

Frequency of oscillations

\( \rho \) :

Density of the fluid

*:

Represent the dimensional variable

References

  1. Raptis AA, Perdikis CP (1985) Oscillatory flow through porous medium by the presence of free convective flow. Int J Eng Sci 23:51–55

    Article  MATH  Google Scholar 

  2. Singh KD, Mathew A (2012) An oscillatory free convective flow through porous medium through in a rotating vertical porous channel. Global J Sci Front Res 12(3):51–64

    Google Scholar 

  3. Skelland AHP (1976) Non-Newtonian flow and heat transfer. Wiley, New York

    Google Scholar 

  4. Cho YI, Hartnett JP (1985) Non-Newtonian fluids. McGraw-Hill, New York

    Google Scholar 

  5. Hartnett JP (1992) Viscoelastic fluid: a new challenge in heat transfer. ASME Trans 114:296–303

    Article  Google Scholar 

  6. Bhatnagar PL (1966) Laminar flow of an elastico-viscous fluid between two parallel walls with heat transfer. ZAMP 17(5):646–649

    Article  ADS  Google Scholar 

  7. Nabil TM, Eldabe Galal MM, Hoda SA (2003) Magneto hydrodynamic flow of non-Newtonian viscoelastic fluid through a porous medium near an accelerated plate. Can J Phys/Rev Can Phys 81(11):1249–1269

    Article  ADS  Google Scholar 

  8. Singh AK, Singh NP (1996) MHD flow of a dusty visco-elastic liquid through a porous medium between two inclined parallel plates. Proc Natl Acad Sci India 66A:143–150

    Google Scholar 

  9. Rahman MM, Sarkar MSA (2004) Unsteady MHD flow of visco-elastic Oldroyd fluid under time varying body forces through a rectangular channel. Bull Calcutta Math Soc 96:463–470

    MATH  Google Scholar 

  10. Rajgopal K Veena PH, Pravin VK (2006) Oscillatory motion of an electrically conducting viscoelastic fluid over a stretching sheet in saturated porous medium with suction/blowing. Math Probl Eng Article ID 60560:1–14

    Google Scholar 

  11. Reddy PS, Nagarajan AS, Sivaiah M (2008) Hydromagnetic elastic free convection of a conducting elastic–viscous liquid between heated vertical plates. J Naval Archit Marine Eng 2:47–56

    Google Scholar 

  12. Attia HA, Ewis KM (2010) Unsteady MHD Couette flow with heat transfer of a viscoelastic fluid under exponential decaying pressure gradient. Tamkang J Sci Eng 13(4):359–364

    Google Scholar 

  13. Choudhury R, Das UJ (2012) Heat transfer to the MHD oscillatory visco-elastic flow in a channel filled with porous medium. Hindawi Publishing Corporation. Phys Res Int Article ID 879537:1–5

    Google Scholar 

  14. Singh KD (2012) Visco-elastic mixed convection MHD oscillatory flow through a porous medium filled in a vertical channel. Int J Phys Math Sci 3(1):194–205

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics & Statistics, H. P. University, Shimla, India

    Khem Chand & Sanjeev Kumar

  2. Department of Mathematics (ICDEOL), H. P. University, Shimla, India

    K. D. Singh

Authors
  1. Khem Chand
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. D. Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sanjeev Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Khem Chand.

Appendix

Appendix

$$ \begin{aligned} l^{2} = 2i\Upomega ,\quad m^{2} = i\left( {2\Upomega + \omega } \right),\quad n^{2} = i\left( {2\Upomega - \omega } \right), \\ r^{2} = \left( {1 - \frac{{iK_{0} \omega }}{{\lambda^{2} }}} \right),\quad s^{2} = \left( {1 + \frac{{iK_{0} \omega }}{{\lambda^{2} }}} \right), \\ {m}_{1} = \frac{{{P}_{r} \lambda + \sqrt {\left( {{P}_{r} \lambda } \right)^{2} + 4{\text{i}}\omega {P}_{r} } }}{2},\quad {m}_{2} = \frac{{{P}_{r} \lambda - \sqrt {\left( {{P}_{r} \lambda } \right)^{2} + 4{\text{i}}\omega {P}_{r} } }}{2}, \\ {m}_{3} = \frac{{{P}_{r} \lambda + \sqrt {\left( {{P}_{r} \lambda } \right)^{2} - 4{\text{i}}\omega {P}_{r} } }}{2},\quad {m}_{4} = \frac{{{P}_{r} \lambda - \sqrt {\left( {{P}_{r} \lambda } \right)^{2} - 4{\text{i}}\omega {P}_{r} } }}{2}, \\ {n}_{1} = \frac{{\lambda + \sqrt {\lambda^{2} + 4\left( {{\text{l}}^{2} + \frac{1}{\text{K}}} \right)} }}{2},\quad {n}_{2} = \frac{{\lambda - \sqrt {\lambda^{2} + 4\left( {{\text{l}}^{2} + \frac{1}{\text{K}}} \right)} }}{2}, \\ {n}_{3} = \frac{{\lambda + \sqrt {\lambda^{2} + 4{\text{r}}^{2} \left( {{m}^{2} + \frac{1}{\text{K}}} \right)} }}{{2{\text{r}}^{2} }},\quad {n}_{4} = \frac{{\lambda - \sqrt {\lambda^{2} + 4{\text{r}}^{2} \left( {{m}^{2} + \frac{1}{\text{K}}} \right)} }}{{2{\text{r}}^{2} }}, \\ {n}_{5} = \frac{{\lambda + \sqrt {\lambda^{2} + 4{\text{s}}^{2} \left( {{n}^{2} + \frac{1}{\text{K}}} \right)} }}{{2{\text{s}}^{2} }},\quad {n}_{6} = \frac{{\lambda - \sqrt {\lambda^{2} + 4{\text{s}}^{2} \left( {{n}^{2} + \frac{1}{\text{K}}} \right)} }}{{2{\text{s}}^{2} }}, \\ {A}_{1} = \frac{{ - {\text{G}}_{\text{r}} \lambda^{2} }}{{\left( {1 - {\text{e}}^{{\lambda {P}_{r} }} } \right)\left\{ {\lambda^{2} {P}_{r} \left( {{P}_{r} - 1} \right) - \left( {{\text{l}}^{2} + \frac{1}{\text{K}}} \right)} \right\}}}, \\ {A}_{2} = \frac{{ - {\text{G}}_{\text{r}} \lambda^{2} {\text{e}}^{{{m}_{1} }} }}{{{\text{e}}^{{{m}_{1} }} - {\text{e}}^{{{m}_{2} }} \left\{ {{\text{r}}^{2} {m}_{2}^{2} - \lambda {m}_{2 - } \left( {{m}^{2} + \frac{1}{\text{K}}} \right)} \right\}}}, \\ {A}_{3} = \frac{{{\text{G}}_{\text{r}} \lambda^{2} {\text{e}}^{{{m}_{2} }} }}{{{\text{e}}^{{{m}_{1} }} - {\text{e}}^{{{m}_{2} }} \left\{ {{\text{r}}^{2} {m}_{1}^{2} - \lambda {m}_{1 - } \left( {{m}^{2} + \frac{1}{\text{K}}} \right)} \right\}}}, \\ {A}_{4} = \frac{{ - {\text{G}}_{\text{r}} \lambda^{2} {\text{e}}^{{{m}_{3} }} }}{{{\text{e}}^{{{m}_{3} }} - {\text{e}}^{{{m}_{4} }} \left\{ {{\text{s}}^{2} {m}_{4}^{2} - \lambda {m}_{4 - } \left( {{n}^{2} + \frac{1}{\text{K}}} \right)} \right\}}}, \\ {A}_{5} = \frac{{{\text{G}}_{\text{r}} \lambda^{2} {\text{e}}^{{{m}_{4} }} }}{{{\text{e}}^{{{m}_{3} }} - {\text{e}}^{{{m}_{4} }} \left\{ {{\text{s}}^{2} {m}_{3}^{2} - \lambda {m}_{3 - } \left( {{n}^{2} + \frac{1}{\text{K}}} \right)} \right\}}}, \\ \end{aligned} $$
$$ \begin{aligned} {B}_{1} = - \left\{ {\frac{{{\text{e}}^{{{n}_{2} }} + {A}_{1} \left( {{\text{e}}^{{{n}_{2} }} - {\text{e}}^{{\lambda {P}_{r} }} } \right)}}{{{\text{e}}^{{{n}_{2} }} - {\text{e}}^{{{n}_{1} }} }}} \right\}, \\ {B}_{2} = \left\{ {\frac{{{\text{e}}^{{{n}_{1} }} + {A}_{1} \left( {{\text{e}}^{{{n}_{1} }} - {\text{e}}^{{\lambda {P}_{r} }} } \right)}}{{{\text{e}}^{{{n}_{2} }} - {\text{e}}^{{{n}_{1} }} }}} \right\}, \\ {B}_{3} = - \left\{ {\frac{{{\text{e}}^{{{n}_{4} }} + {A}_{2} \left( {{\text{e}}^{{{n}_{4} }} - {\text{e}}^{{{m}_{2} }} } \right) + {A}_{3} \left( {{\text{e}}^{{{n}_{4} }} - {\text{e}}^{{{m}_{1} }} } \right)}}{{{\text{e}}^{{{n}_{4} }} - {\text{e}}^{{{n}_{3} }} }}} \right\}, \\ {B}_{4} = \left\{ {\frac{{{\text{e}}^{{{n}_{3} }} + {A}_{2} \left( {{\text{e}}^{{{n}_{3} }} - {\text{e}}^{{{m}_{2} }} } \right) + {A}_{3} \left( {{\text{e}}^{{{n}_{3} }} - {\text{e}}^{{{m}_{1} }} } \right)}}{{{\text{e}}^{{{n}_{4} }} - {\text{e}}^{{{n}_{3} }} }}} \right\}, \\ {B}_{5} = - \left\{ {\frac{{{\text{e}}^{{{n}_{6} }} + {A}_{4} \left( {{\text{e}}^{{{n}_{6} }} - {\text{e}}^{{{m}_{4} }} } \right) + {A}_{5} \left( {{\text{e}}^{{{n}_{6} }} - {\text{e}}^{{{m}_{3} }} } \right)}}{{{\text{e}}^{{{n}_{6} }} - {\text{e}}^{{{n}_{5} }} }}} \right\}, \\ {B}_{6} = \left\{ {\frac{{{\text{e}}^{{{n}_{5} }} + {A}_{4} \left( {{\text{e}}^{{{n}_{5} }} - {\text{e}}^{{{m}_{4} }} } \right) + {A}_{5} \left( {{\text{e}}^{{{n}_{5} }} - {\text{e}}^{{{m}_{3} }} } \right)}}{{{\text{e}}^{{{n}_{6} }} - {\text{e}}^{{{n}_{5} }} }}} \right\}. \\ \end{aligned} $$

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chand, K., Singh, K.D. & Kumar, S. Oscillatory Free Convective Flow of Viscoelastic Fluid Through Porous Medium in a Rotating Vertical Channel. Proc. Natl. Acad. Sci., India, Sect. A Phys. Sci. 83, 333–342 (2013). https://doi.org/10.1007/s40010-013-0095-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40010-013-0095-3

Keywords

Search

Navigation