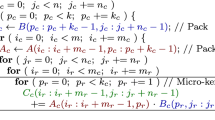Parallel GEMM-based convolution for deep learning on multicore RISC-V processors

Abstract

We address the efficient implementation of the convolution operator on the GAP8 parallel ultra-low power platform (PULP), a heterogeneous multi-core processor equipped with a fabric controller (FC); a cluster of eight compute cores; and a four-level memory hierarchy with scratchpads instead of conventional, hardware-assisted cache memories. Our solution for this platform transforms the convolution into a general matrix–matrix multiplication (gemm) via the lowering approach, demonstrating that it is possible to attain reasonable performance on the GAP8 by carefully adapting techniques such as tiling and loop parallelism, which are mainstream in the multi-threaded, cache-aware realization of gemm.

1 Introduction

Implementing deep learning (DL) algorithms on edge devices for Internet of things (IoT) applications is critical to enhance privacy and security. In addition, moving the computation from the cloud to IoT nodes closer to sensors can significantly reduce the amount of data sent over the network, thereby reducing latency and energy consumption [1,2,3]. The wide variety of IoT applications, many of which rely on DL technologies, has led to a broad range of edge processor architectures, including cores with RISC-V ISA (instruction set architecture) [4]. This diversity, combined with severe constraints on power, memory capacity and computational performance for edge devices, asks for a careful selection of algorithms and the optimization of the software running on them.

In this work, we focus on the implementation of convolutional deep neural networks (DNNs) on edge processors. With this objective, we parallelize a popular algorithm for the convolution operator based on the lowering approach, which decomposes the operation into a data replication transform, known as im2col or im2row, followed by a general matrix–matrix multiplication (gemm) [5]. Moreover, we target the heterogeneous 1+8 RISC-V cores integrated into the GAP8 parallel ultra-low power platform (PULP) for IoT. In more detail, this paper makes the following contributions:

• We develop a high-performance, multi-threaded implementation of gemm that operates with 8-bit integer (INT8) data and arithmetic on top of the dot (scalar or inner) product, a basic kernel that receives special support in the GAP8. In our solution, the 8 compute cores of the GAP8 are in charge of all the arithmetic while the remaining core, known as the fabric controller (FC), coordinates the data movements.

• We orchestrate a careful sequence of data transfers across the memory areas of the GAP8 via DMA transfers, embedding these movements into the tiling techniques of a parallel blocked algorithm for gemm.

• We perform a complete experimental evaluation of the convolution realization for the two aforementioned transforms: im2col and im2row.

The rest of the paper is structured as follows. In Sect. 2 we briefly present the convolution operator and in Sect. 3 we review the high-performance implementation of gemm on multicore processors with a multilayered memory including caches. In Sect. 4 we detail the main features of the GAP8 platform. In Sect. 5 we describe the approach to obtain a parallel high-performance algorithm for gemm on the GAP8 system. In Sect. 6, we evaluate the resulting routine. Finally, in Sects. 7 and 8 we close the paper with a general discussion and a few concluding remarks.

2 Convolution via IM2COL+GEMM

In this section, we first introduce the convolution operation [6] to then present the im2col and im2row transforms which, combined with gemm, potentially yield a high-performance approach to compute this operator, at the cost of an augmented workspace and some data copies [5].

2.1 Convolution

The inference process for a Conv layer requires the application of a convolution operator. This operation receives an input activation tensor I, of dimension $b \times c_i \times h_i \times w_i$, where b is the number of input images or samples (also known as batch size), $c_i$ specifies the number of input image channels, and $h_i\times w_i$ are the input image height $\times$ width. In addition, the convolution also receives an input filter (or kernel) tensor F, of dimension $c_o \times c_i \times h_f \times w_f$, where $c_o$ is the number of filters and $h_f\times w_f$ denote the filter height $\times$ width. Following with the operator definition:

$$\begin{aligned} O = {\textsc {Conv}}(F,\,I), \end{aligned}$$

(1)

returns the output activation tensor O, of dimension $b \times c_o \times h_o \times w_o$, where $c_o$ specifies the number of output channels and $h_o \times w_o$ are the output image height $\times$ width.

The algorithm in Figure 1 provides a direct realization of the convolution operator. There, each individual filter combines a subset of the inputs, with the same dimension as the filter, to produce a single scalar value (or entry) in one of the $c_o$ outputs. By repeatedly applying the filter to the whole input, with a certain horizontal/vertical stride s, the convolution operator thus obtains the entries of this single output [6]. Assuming vertical and horizontal padding factors given by $p_h$ and $p_w$, respectively, the output height $\times$ width dimensions are given by $h_o \times w_o = \lfloor (h_{i}-h_f + 2 p_h)/s +1\rfloor \times \lfloor (w_{i}-w_f + 2 p_w)/s +1\rfloor$.

Fig. 1

Direct algorithm for the application of the convolution operator $O = {\textsc {Conv}}(F,\,I)$

2.2 Indirect convolution via the im2col/im2row transforms

Fig. 2

Algorithm for the im2col transformation

On current computer architectures, the performance of the direct algorithm in Figure 1 is strongly constrained by the memory bandwidth and, therefore, this approach in general delivers only a fraction of the processor peak floating-point throughput. In practice, this drawback is usually tackled by adopting an indirect or gemm-based approach which casts this operator in terms of a matrix multiplication via either the im2col or im2row transform [5]. This realization is often referred to as the lowering algorithm.

In short detail, Figure 2 displays the im2col algorithm¹ that “flattens” the four-dimensional (4D) input tensor I into an augmented (2-dimensional, 2D) matrix $\hat{B}$ so that the output of the convolution can be then obtained from the gemm

$$\begin{aligned} \hat{C} = \hat{A}\cdot \hat{B}, \end{aligned}$$

where $\hat{C} \equiv O \rightarrow m \times n = c_o \times (h_o \cdot w_o \cdot b)$ is the convolution output (viewed as a 2D matrix, with $m=c_o$ and $n=h_o \cdot w_o \cdot b$); $\hat{A} \equiv F \rightarrow m \times k = c_o \times (h_f \cdot w_f \cdot c_i)$ contains a 2D organization of the filters; and $\hat{B} \rightarrow k \times n = (h_f \cdot w_f \cdot c_i) \times (h_o \cdot w_o \cdot b)$ is the aforementioned augmented matrix. For simplicity, the algorithm shown in Figure 2 does not take into account the memory access when the stride of the convolution is higher than one. In addition, the actual implementation of this transform eliminates some of the loop invariants inside several loops to reduce the indexing overhead.

3 Blocked algorithms for GEMM

With the convolution operator flattened into a matrix multiplication via the im2col (or im2row) transform, this section reviews the conventional strategy to obtain a high-performance realization of gemm on current processor architectures with deep cache memory hierarchies and single-instruction multiple-data (SIMD) vector units.

3.1 The baseline algorithm for GEMM

Fig. 3

B3A2C0 (top) and B3C2A0 (bottom) algorithms for gemm

Current high-performance implementations of gemm, in both open-source and commercial linear algebra libraries, follow GotoBLAS [7] to formulate this kernel as a collection of five nested loops around two packing routines and a micro-kernel; see Figure 3 (top). In rough detail, the instances of gemm in these libraries apply tiling (blocking) as follows:

• A $k_c \times n_c$ block of matrix B is packed into a buffer $B_c$, intended to reside in the L3 cache memory (or main memory, in case there is no L3 cache); see line 4 in the algorithm.

• An $m_c \times k_c$ block of matrix A is packed into a buffer $A_c$, designated for the L2 cache memory; line 7.

• During the micro-kernel execution (lines 11–14), a specific $k_c \times n_r$ block of $B_c$, referred to as the micro-panel $B_r$, is expected to lie in the L1 cache memory.

• The micro-kernel performs the arithmetic, in principle accessing the data for $A_c$ from the L2 cache, for $B_r$ from the L1 cache, and for C directly from main memory.

The data transfers across the memory hierarchy are illustrated in Figure 4. In addition, packing $A_c,B_c$ as in Figure 5 ensures that their entries are retrieved with unit stride from the micro-kernel. The baseline algorithm for gemm, also referred as B3A2C0,² features a micro-kernel that includes the sixth loop, iterating over the $k_c$ dimension. This component of the algorithm is the only one encoded directly in assembly or in C with vector intrinsics; see Figure 3 (top). At each iteration of the loop, the micro-kernel updates an $m_r \times n_r$ micro-tile of C, say $C_r$, by performing an outer product involving (part of) one row of the buffer $A_c$ and one column of the micro-panel $B_r$.

Fig. 4

The baseline algorithm of gemm B3A2C0. Here $C_r$ is a notation artifact, introduced to ease the presentation of the algorithm while $A_c$ and $B_c$ are actual buffers that maintain copies of certain blocks of A and B

Fig. 5

Packing in the baseline algorithm of gemm B3A2C0. Note how the entries of A, B are reorganized into $A_c,B_c$ in micro-panels of $m_r$ rows, $n_r$ columns, respectively

3.2 Alternative algorithms for GEMM

By re-arranging the gemm loops in the baseline algorithm in Figure 3 (top) in a distinct order, combined with an appropriate selection of the loop strides, we can obtain different algorithmic variants of gemm, which favor that certain blocks of A, B, C reside in distinct levels of the memory hierarchy [8,9,10]. Concretely, Figure 3 allows a visual comparison between the codes for the B3A2C0 (baseline) and B3C2A0 variants, implicitly exposing the following major differences between the two:

• In B3C2A0, an $m_c \times n_c$ block of C is packed into a buffer $C_c$ for the L2 cache; line 7 in the algorithm. Moreover, this variant also requires an unpacking step that moves the entries of $C_c$ into C once the micro-kernel is executed; line 16.

• In order to ensure accessing the entries of C, B with unit stride from the micro-kernel for B3C2A0, both $C_c$ and $B_c$ are stored following the same pattern shown for $A_c$ in Figure 5, with the entries of $C_c$ arranged into micro-panels of $m_r$ rows and those of $B_c$ into micro-panels of $k_r$ rows.

• The micro-kernel for B3C2A0 operates with a $m_r \times k_r$ micro-tile of A streamed directly from the memory into the registers, where it will reside during the full execution of the micro-kernel. This performs a small, $m_r \times k_r$ matrix-vector product per iteration of Loop L6 (for a total of $n_c$ iterations), each involving a single column of a micro-panel $C_r$ and a single column of a micro-panel $B_r$; lines 11–14.

As we will discuss in Sect. 4, variant B3C2A0 presents several characteristics that make it especially interesting for its implementation on the GAP8 platform.

4 The GAP8 Platform

The GAP8 is a commercial platform designed for IoT applications, with a processor based on the PULP [11] architecture. As depicted in Figure 6, the GAP8 processor embeds three main computing components: (1) A low-power microcontroller unit (MCU), known as the FC, which is responsible for managing control, communications, and security functions; (2) a compute engine (CE) comprising a cluster of 8 compute cores specifically designed for the execution of parallel algorithms; and (3) a specialized hardware accelerator (HWCE) that is part of the CE as well.

Fig. 6

GAP8 layout

The FC integrates a read-only memory (ROM) that stores the primary boot code, plus a private 16-KB L1 scratchpad (also referred to as memory area or MA). On the CE side, the compute cores and the HWCE share a 64-KB multi-banked tightly coupled data memory (TCDM) L1 scratchpad (MA). Moreover, FC and CE share a 512-KB L2 scratchpad. The device also includes an 8-MB L3 MA that acts as the platform main memory and is accessible from the FC. To enable rapid data transfers between MAs, the platform features two direct memory access (DMA) units. One of these units assists in transferring data between the FC domain and the CE domain, while the micro-DMA unit transfers data to/from peripherals, including the L3 MA.

Both the FC and the cluster cores support the RISC-V RV32IMCXpulpV2 instruction set architecture (ISA), which includes integer (I) arithmetic, compressed instructions (C), multiplication and division (M) extensions, and a portion of the supervisor ISA subset. The RV32ICMXpulpV2 ISA extension also provides specialized instructions for zero overhead hardware loops, pointer post/pre-modified memory accesses, instructions mixing control flow with computation, multiply/subtract and accumulate, vector operations, fixed point operations, bit manipulation, and the dot product of two vectors.

5 Tailoring GEMM for the GAP8

In this section, we describe our adaptation of gemm to run in parallel on the compute cores integrated into the GAP8 CE. This customization effort is strongly dictated by the following features of the GAP8 platform:

• The compute cores offer special hardware for the dot product.

• The memory hierarchy in the platform is structured into four levels: vector registers, two intermediate scratchpad levels (L1, L2 MAs), and a main memory (also referred to as RAM or L3 MA).

• The system integrates scratchpads instead of conventional cache memories.

• A single FC controls the memory transfers between main memory and the L1, L2 scratchpads.

• The CE features 8 compute cores.

As a first step, we followed the work described in [12], which addressed the sequential implementation of gemm on the FC, modifying that solution to target the compute cores in the CE. The resulting code operates with signed INT8 numbers and presents the specific features described in the remainder of this section.

5.1 Micro-kernel for B3C2A0

A first aspect to note is that, as the FC and compute cores support the same RISC-V-oriented ISA, including the specialized instructions for the dot product and the vector registers, adapting the initial FC micro-kernel from [12], to the cluster cores basically required no changes. To illustrate this, Figure 7 displays a simplified version of a micro-kernel that operates with a $4 \times 4$ micro-tile $A_r$, implementing the innermost loop in the B3C2A0 algorithm (see lines 11–14 in Figure 3 right) as follows:

• The micro-kernel receives as input parameters (1) the starting address in main memory of the micro-tile $A_r$ (parameter Ar), which is assumed to be stored in row-major order; (2) the leading dimension of the matrix operand A (parameter ldA); (3) the starting address of the micro-panel $B_r$ (parameter Br) in the L1 MA of the CE; and (4) the starting address of the micro-panel $C_r$ embedded in $C_c$ (parameter Cc) in the L2 MA shared with the FC.

• The code for the micro-kernel next includes the corresponding variable declarations of scalar and vector data (lines 4–6). The data type for the latter is v4s, which identifies a vector with capacity for four INT8 numbers.

• The code then loads the four rows (with four INT8 numbers each) of the $4 \times 4$ micro-tile $A_r$ into the same number of vector registers: A0, A1, A2, A3 (lines 9–10).

• At each iteration of the main loop (line 12), the micro-kernel loads one column of the micro-panel $C_r$ (four INT8 numbers) into the vector register cr and one column of the micro-panel $B_r$ (four INT8 numbers) into the vector register br (lines 14–15).

• Inside the loop, the micro-kernel then proceeds to multiply the contents of the micro-tile $A_r$ with the column of $B_r$, updating the column of $C_r$ via four dot products (lines 18–19); and storing the four INT8 elements in the column of $C_r$ back into the L2 MA (lines 22–23).

At this point we note that we have implemented and tested micro-kernels of different “shapes” (or dimensions) $m_r \times k_r$. Also, while the same micro-kernel can basically run on the FC and a single compute core, the data for the matrix operands must be placed into the appropriate MAs, which are different depending on which component (FC or compute core) has to execute the micro-kernel. We discuss this point in detail next.

Fig. 7

Simplified realization of the sequential implementation of a micro-kernel with an $m_r \times k_r = 4 \times 4$ micro-tile of A resident in the processor (FC or compute core) registers for the B3C2A0 variant of gemm

5.2 Data transfers across the memory hierarchy

The GAP8 platform integrates L1 and L2 scratchpads, which give the programmer full control over the data transfers across the memory hierarchy but also the responsibility to orchestrate them. Our solution targeting the compute cores in the CE addresses this task by embedding the data movements naturally into the B3C2A0 algorithm as follows:

• The FC packs B into the buffer $B_c$, with both data operands residing in the main memory. Thus, this data movement only involves the “hardware” in the MCU (scratchpads and core).

• The FC packs the data for C into $C_c$, in this case transferring it from the memory to the L2 MA in the MCU. The transfer for the unpacking is also governed by the FC, but obviously carried out in the opposite direction. Again, these copies only involve the MCU part of the GAP8.

• The FC copies the micro-panel $B_r$ from $B_c$, from the L2 MA in the MCU to the L1 MA in the CE.

• The compute core that executes a micro-kernel expects that the data for $B_r$ resides in the L1 MA, for $C_c$ in the L2 MA, and for A in the main memory. However, the CE cannot directly access the data in the main memory, and therefore the FC copies the appropriate micro-tiles of A from there to the L1 MA in the CE. Next, inside the micro-kernel, each core streams the data of its own micro-tile from the L1 to its vector registers.

The data movements required for the collaboration of FC and compute cores are graphically illustrated in Figure 8. Although the plot there displays the execution of the parallel algorithm, to be discussed next, the data movements in the case of the sequential algorithm are basically the same and can be derived by considering the movements involving Core 1 only.

To close this subsection, we remind that the loop strides for the B3C2A0 algorithm are set to $n_c,k_c,m_c,m_r,k_r$ (respectively, for loops L1, L2,..., L5; see Figure 3 (right)). The last two variables, $m_r,k_r$, determine the shape of the micro-kernel and are usually adjusted depending on the number of vector registers per core. The first three variables are known as the cache configuration parameters, and they should be set according to the dimensions of the L1, L2, and L3 memory levels as well as the shape of the micro-kernel. For a sequential algorithm targeting a single compute core of the GAP8 platform, we have to take into account that

$$\begin{aligned} \begin{array}{rcl} k_r \times n_c + m_r \times k_r &{} \le &{} \textsf {CL1}, \\ m_c \times n_c &{} \le &{} \textsf {CL2}, \end{array} \end{aligned}$$

where CL1, CL2, respectively, denote the capacity of the L1, L2 MAs accessed by the compute core.

5.3 Parallelization

Fig. 8

Data movements in the parallel version of the B3C2A0 algorithm. For simplicity, the data transfers corresponding to the streaming of the columns $c_r^0, c_r^1,\ldots ,c_r^7$ from the corresponding 8 micro-panels of $C_c$ into the processor registers are annotated with arrows only for Core 1. The same applies from the streaming (replication) of the column $b_r$ from the micro-panel $B_r$, and the streaming of the 8 micro-tiles $A_r^0, A_r^1,\ldots ,A_r^7$ from A

Following the conventional approach for the multi-threaded realization of gemm, we exploit loop parallelism for the B3C2A0 algorithm. The first question thus is which of the six loops appearing in the algorithm to target. In order to take this decision, we make the following observations about the code in Figure 3 (right):

• Parallelizing Loop L1 (indexed by jc) partitions the operation into a collection of independent gemm kernels. The consequence is that this requires separate workspaces per thread for the $C_c,B_c,B_r$ buffers in each memory level, in practice dividing the capacity of these memories among the threads. Given that the compute cores in the CE share the L1, L2 MAs and, obviously, the main memory, this does not seem the best approach for an efficient collaboration.

• A parallel algorithm targeting loops L2 (indexed by pc) or L4 (indexed by pr) faces race conditions because multiple threads may then update the same parts of the output matrix at the same time. It is possible to control this type of behavior using various software techniques (and, in some cases, hardware mechanisms), but in general they introduce a non-negligible overhead.

• Parallelizing loop L3 (indexed by ic) would require a separate buffer per thread for $C_c,B_r$. Therefore, for the same reasons as exposed for loop L1, this does not seem a good option from an inter-core collaboration perspective.

This analysis leaves only loops L5 (indexed by ir) or L6 (indexed by jr, inside the micro-kernel,) as potential candidates. To increase the granularity of the workload distribution and reduce thread synchronization we therefore choose the outermost option: loop L5. The memory target of the distinct operands and buffers and the data movements for the parallel algorithm are illustrated in Figure 8. Note that, with the selected parallelization scheme, all the compute cores access the same $m_c \times n_c$ buffer $C_c$ in the L2 MA, the same $k_r \times n_c$ micro-panel $B_r$ in the L1 MA, but a different $m_r \times k_r$ micro-tile $A_r$ in the L1 MA. For this reason, in the parallel case, the micro-kernel shape and cache configuration parameters must satisfy

$$\begin{aligned} \begin{array}{rcl} k_r \times n_c + c\, (m_r \times k_r) &{} \le &{} \textsf {CL1}, \\ m_c \times n_c &{} \le &{} \textsf {CL2}, \end{array} \end{aligned}$$

where c specifies the number of cores that participate in the parallel execution.

To fully leverage the capabilities of the GAP8 processor and improve the overall performance, we distribute the iteration space for loop L5 evenly across the 8 RISC-V compute cores in the GAP8 CE. Figure 9 displays the fragment of the parallel code that comprises loop L5 plus the invocation to the micro-kernel. The main differences with the sequential counterpart are:

• All the cluster compute cores iterate over the ir loop, but each core only executes its “own” iterations. The workload is distributed following a simple round-robin policy with “chunks” of mr rows (see lines 10–11 in the algorithm).

• The core in charge of executing a given micro-kernel instructs the FC to copy the $m_r \times k_r$ micro-tile $A_r$ from the memory to L1 MA (lines 14–18).

• The core then executes the micro-kernel by invoking the sequential code presented earlier (line 21), and prepares the variables and address pointers for the next iteration (line 23). Remind that, from inside the micro-kernel, the core streams $A_r$ from L1 to its vector registers.

• Synchronization points are included in lines 17 and 25. The former ensures that the data are already copied in the L1 MA, while the latter is for overall thread synchronization.

Fig. 9

Simplified realization of the parallel implementation of loop L5 for the B3C2A0 variant of gemm

We finally come back to the convolution operator to note that, in the case of the im2col transform, matrix $\hat{A}$ contains the operator filters and, for inference, this tensor remains constant. The same applies to $\hat{B}$ in the case of the im2row transform. In the next section we describe how we can take advantage of this to pre-pack the filter tensor and eliminate/accelerate some of the data transfers for the B3C2A0 algorithm.

6 Performance Analysis

In this section, we evaluate the performance of the convolution operator based on the lowering approach, discussing the differences between the im2col or the im2row variants.

Table 1 Parameters of the convolution layers arising in MobileNet-v1 and dimensions of the gemm obtained with the application of the im2col transform

6.1 Setup

We have evaluated the performance of our parallel gemm-based convolution in the GAP8 platform using a real DL model and INT8 arithmetic. Specifically, we ran the inference phase for the convolutional layers in the MobileNet-v1 DNN, setting the input batch size b to 1 (i.e., a single input scenario). For this purpose, we preprocess the convolution operators using either the im2col or the im2row transform, obtaining gemm kernels of the form $\hat{C} =\hat{A} \cdot \hat{B}$ that operate with augmented matrices of different dimensions; see Sect. 2 and Table 1.

The results reported in this section are averaged for a 30-second execution of each experiment. We have implemented and tested micro-kernels of varying dimensions $m_r \times k_r$. For brevity, for each convolution operator we only report the results obtained with the best-performing micro-kernel. For layers 1–2, 4–7, and 11–27 of MobileNet-v1, this corresponds to a micro-kernel with $m_r \times k_r = 4 \times 24$. For layers 3 and 8–10, the best micro-kernel was $m_r \times k_r = 4 \times 20$.

Fig. 10

Distribution of costs for layer #10 of MobileNet-v1 using im2col+gemm (top) and im2row+gemm (bottom)

The variety of micro-kernels that can be implemented is strongly constrained by the number of vector register in the hardware which, in turn, is quite low (usually, around 32). In consequence the number of micro-kernels is also limited. In our experiments, we implemented the micro-kernel as part of an incremental process, starting with $m_r \times k_r = 4 \times 4, 4 \times 8$ and $8 \times 4$. We then guided our development effort by implementing additional micro-kernels (e.g., $m_r \times k_r = 4 \times 16, 16 \times 4$), testing their performance, and observing the trend as either $m_r$ or $k_r$ was increased. This allowed us to determine an optimal micro-kernel without the effort of implementing them all.

6.2 Preliminary analysis

As a starting point for our analysis, Figure 10 breaks down the time spent in layer 10 of MobileNet-v1 into the different components of the algorithm:

• Arithmetic (by compute cores),

• Stream_Cc (from L2 to registers by compute cores),

• Stream_Br (from L1 to registers by compute cores),

• Stream_A (from L3 to L1 by FC, and from there to registers by compute cores),

• Copy_Br (from L3 to L1 by compute cores),

• Pack_Cc (from L3 to L2 by FC),

• Unpack_Cc (from L2 to L3 by FC), and

• Pack_Bc (from L3 to L3 by FC);

see Sect. 4 and Figure 8. The figure displays two plots, for the im2col- and im2row-based convolution variants, and reports the execution time (in seconds) using 1, 4 and 8 compute cores.

For reference, we first analyze the transfer costs and how they impact the efficiency of the sequential implementation. For brevity, we focus this study on layer #10 and the im2col transform. From Figure 10, we observe that the arithmetic cost for this layer is 3.73 s, which offers a sustained peak of about 247 MOPS. In comparison, the transfer costs amount to 3.70 s, which offers an efficiency that is close to 50% when we run the algorithm on a single core of the CE. Also for reference, in [13] we measured and reported the sustained arithmetic performance as well as the sustained bandwidth between different levels of the memory hierarchy.

Let us turn our attention next to the parallel implementation. From the plots in Figure 10, it is clear that the two first components, Arithmetic and Stream_Cc, significantly benefit from a parallel execution. In contrast, there is a different behavior for many other components, with a very small decrease of the execution time when using 4 compute cores and a negligible benefit for 8 compute cores. The explanation in all these cases is common: Those components that are executed inside the loop that is parallelized in our solution (loop L5), for which in addition there is no participation of FC, truly run in parallel and consequently are accelerated in a multi-threaded execution. This is the case of Arithmetic, Stream_Cc, Stream_Br, and Copy_Br. In comparison, the remaining components require the participation of FC (basically to program the DMA transfers from/to L3) and, therefore, they are intrinsically sequential as there is only one FC. For the sequential execution, the cost is dominated by Arithmetic followed by Stream_Cc and, for the im2row variant, Stream_A. The lack of parallel scalability of the latter component for im2row exerts a strong impact on the cost of the parallel executions for that variant.

A significant difference between the costs of the im2col and im2row variants is visible for Stream_A. The reason is mainly that this cost is proportional to the dimension m of the gemm associated with this layer: 256 for im2col and 784 for im2row (see Table 1). In addition, for im2col the filter matrix corresponds to the gemm matrix operand $\hat{A}$. Therefore, we have accelerated this type of transfer, from the main memory to the L1 MA, by (1) pre-packing the operand, so that the $m_r \times k_r$ elements of each micro-tile lie in contiguous positions in main memory; and (2) programming the DMA/FC to copy the $(m_r \cdot k_r)$ elements of the micro-tile with a single call. This allows to replace the loop in lines 14–18 of Figure 9 with a single call to pi_cl_ram_read$+$pi_cl_ram_read_wait.

Finally, comparing the distributions of costs between the im2col and im2row variants, we observe that there is no cost associated with Pack_Bc for the latter. The reason is that, for im2row, the gemm matrix operand $\hat{B}$ corresponds to the convolution filters, which remain constant during the inference stage. In consequence, we can pre-pack this matrix (and re-utilize it for any number of subsequent inferences) so that the re-organization of the matrix becomes unnecessary. In contrast, for im2row the matrix operand $\hat{A}$ corresponds to the augmented matrix that results from applying the transform to the input activation tensor. As these data vary from one sample to the next, we cannot pre-pack it. Therefore, for im2row we cannot benefit from the faster transfers of the micro-tiles between main memory and L1 described in the previous paragraph.

6.3 Global comparison

Fig. 11

Performance attained for the convolutional layers in MobileNet-v1 using im2col+gemm (top) and im2row+gemm (bottom). The results with one core display the arithmetic rate (in millions of INT8 operations per second, or MOPS) observed with the “sequential” algorithm, executed using a single compute core and the FC

Figure 11 shows the performance rates for all layers of MobileNet-v1, attained with the “sequential” version³ of the two convolution variants (im2col and im2row) as well as the corresponding speedup observed with the parallel counterpart, using 4 and 8 compute cores. In general, the sequential version using im2col slightly outperforms the alternative based on im2row for the initial layers (1–11), but it is scantly inferior for the final layers. The reason for the similar behavior is that, in the sequential case, (1) there are no differences for Arithmetic, since both variants obviously perform the same number of arithmetic operations and this component does not include any data transfer cost; furthermore, (2) the differences between cost of Stream_Cc for the two variants are negligible, as this depends on m, n, and these two values are simply swapped between the two variants. In the parallel case, the factor that can make a difference between im2col and im2row is the lack of scalability of Stream_A, which has a significant contribution to the execution time for the latter. However, this is compensated by the Pack_Bc component for im2col, which contributes a cost that the im2row counterpart does not have to pay.

With respect to the parallel algorithm, on 4 compute cores we observe a maximum speedup of 3.19 for im2col and slightly higher, 3.24, for im2row. With 8 compute cores, the maximum speedup is 5.00 for im2col and again marginally higher, 5.15, for im2row. The average speedup for im2col is 2.96 on 4 compute cores and 4.39 8 compute cores; for im2row, it is 2.71 on 4 compute cores and 4.09 on 8 compute cores.

6.4 im2col versus im2row

The previous discussion exposes the small performance differences between im2col and im2row. In practice, the former type of transform is associated with the so-called NHWC layout of the input/output activation tensors, where the four letters (N,H,W,C), respectively, specify the ordering in memory of the dimensions $(b,h_i/h_o,w_i/w_o,c_i/c_o)$ of the convolution operator. In comparison, the im2row transform is linked with the NCHW layout. This is relevant because, for im2row, it is possible to concatenate two (or more) consecutive convolutional layers (with a number of element-wise layers in between) so that the output activation tensor of one convolution is directly passed as the input activation to the next one. For im2col, in contrast, the concatenation of consecutive convolutional layers requires re-arranging the output activation tensor in memory, previously to passing its data to the next layer. The key here is that the cost of these data re-organization is, in general, not negligible in a platform such as the GAP8.

A potential strategy to accelerate the execution of im2row is to employ an algorithmic variant based on A3C2B0 for gemm instead of B3C2A0. For im2row, the filter matrix corresponds to the gemm matrix operand $\hat{B}$ and, for A3C2C0, this operand can be pre-packed into micro-tiles in the main memory. Therefore, this solution can benefit from the same fast transfers reported earlier for $\hat{A}$ in the im2col variant combined with the B3C2A0 algorithm.

7 General discussion

The GAP8 PULP is a system with some unique features: (1) special hardware support for the dot product; (2) a heterogeneous architecture consisting of the FC plus the eight CE cores; and (3) a four-level memory hierarchy, with the two intermediate levels corresponding to scratchpads instead of the traditional hardware-assisted caches. These characteristics required us to take some special measures to adapt the conventional blocked algorithm for gemm to achieve high performance on the GAP8 PULP, which we discuss next.

First, the support for the dot product forced us to target the B3C2A0 member of the gemm algorithm family, where a small micro-tile of A resides in the processor registers during micro-kernel execution. In contrast, the conventional algorithm for gemm follows a B3A2C0 scheme, where a tile of C resides in the processor register. While one could formulate the B3A2C0 algorithm to rely on the dot product, this comes at the cost of modifying the standard packing routines.

Second, the presence of eight compute cores in the CE, with shared L1/L2/L3 memory levels, is addressed in our parallel algorithm by exploiting loop parallelism at loop L5 (indexed by ir). This implies that, during the execution of the micro-kernel, all threads/cores access the same data from C, A, respectively, residing in the L2, L3 memory areas, which matches the fact that these two levels of memory are shared. However, each thread/core accesses a different micro-panel $B_r$ in the shared L1 scratchpad. In principle, it would be more natural to parallelize the loop L6 so that all threads/cores access different columns of the same micro-panel B. However, this results in a scheme with very fine-grained parallelism, with significant synchronization overhead for the threads.

Third, the integration of the scratchpads forced us to hide the data movements across the memory hierarchy within the packing routines (for packing C from main memory into the L2 scratchpad), or directly include new code transfer routines within the gemm loops (for copying B between main memory and the L1 scratchpad) as well as the micro-kernel (for copying A from main memory and the processor registers). We had to carefully distribute these transfer tasks between the FC and the CE, as these different types of cores have different access rights to different levels of memory.

Overall, the adaptation of gemm to the GAP8 platform required a rethink of the principles underlying modern high-performance implementations of matrix multiplication. Some of the ideas that emerged from this effort are indeed general, and carry over to other platforms with similar characteristics. Two clear examples of this are the formulation of the algorithm to rely on the dot product for architectures with special hardware support for this type of operation and the embedding of data movements within the packing routines. Therefore, while migrating the implementation to other architectures with similar hardware characteristics may require a non-negligible amount of recoding, we are very confident that the ideas described in this work are general and portable.

8 Concluding remarks

We have proposed an efficient implementation of convolution operator, for the GAP8 PULP heterogeneous multicore processor, that leverages the fabric controller for data transfers and the cores in the compute engine for the arithmetic. The GAP8 features a four-level memory hierarchy, with scratchpads instead of conventional caches, plus a fabric controller and 8 compute cores. To target this architecture, our solution transforms the convolution into a gemm, via the lowering approach; applies tiling to partition the gemm matrix operands; and orchestrates the data transfers across the memory hierarchy as part of the packing operations in gemm. In addition, the proposed approach formulates the gemm operation as an algorithm where a small block of A (the micro-tile) is resident in the vector registers of each compute core (in order to cast the innermost computation in terms of a dot product); and exploits parallelism from one of the gemm innermost loops to distribute the workload among the eight compute cores.

Our experiments on the platform, using the MobileNet-v1 model and a single input scenario show small differences in the execution time and parallel scalability between the im2col and im2row variants, though we expect the latter to be more efficient when considering the concatenation of layers that appear in a DNN, especially if it is integrated into a A3C2B0 algorithm for gemm.

As part of future work, we plan to explore the possibilities of overlap** transfers with computation via double buffering. We expect this will reduce the impact of idle times due to communication on the global performance. However, there is a delicate balance to inspect here as it also reduces the re-utilization of the data stored in the buffers, a factor which is relevant due to the small capacity of the scratchpads.