SpringerLink
Log in

Ferromagnetic Chaos in thermal convection of fluid through fractal–fractional differentiations

  • Published:
Journal of Thermal Analysis and Calorimetry Aims and scope Submit manuscript

Abstract

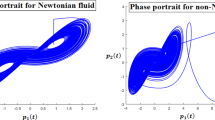
Thermal convection suppresses the thermal stability and instability during the interaction between the magnetic fields because thermal convection is the most significant driver of time-dependent patterns of motion within magnetized and non-magnetized chaotic. In this manuscript, a mathematical modeling is proposed subject to the magnetohydrodynamic conductive fluid lying on an infinite horizontal layer subject to heat from below with gravity. The mathematical model is based on nonlinear ordinary differential equations and such model has been investigated by means of the Boussinesq approximation and Darcy's law. The newly defined techniques of fractal–fractional differential operators, namely Atangana–Baleanu and Caputo–Fabrizio fractal–fractional differentiations, have been imposed on the governing equations. The mathematical analysis based on the equilibrium points and stability criteria is investigated to examine the dynamic responses of a magnetized and non-magnetized conductive fluid model. The numerical simulations have been performed by Adams methods, which is so-called the explicit scheme of the Adams–Bashforth method. Our results suggest that the comparative evolution of trajectories between magnetized and non-magnetized chaotic behaviors has strong effects due to Lorentz force that showed the resistivity in chaotic phenomenon.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Abbreviations

ρ0 :

Reference value of density

V :

Velocity

B :

Applied magnetic field

T :

Temperature

Φ:

Electric potential

p :

Pressure of fluid

Pr:

Prandtl number

\(\aleph_{1} ,\aleph_{2} ,\aleph_{3} ,\aleph_{4}\) :

Letting parameters

\(E_{{{\rm x}_{1} ,{\rm y}_{1} ,{\rm z}_{1} }}^{1} ,E_{{{\rm x}_{1} ,{\rm y}_{1} ,{\rm z}_{1} }}^{2} ,E_{{{\rm x}_{1} ,{\rm y}_{1} ,{\rm z}_{1} }}^{3}\) :

Equilibrium points

\(\tau_{1} ,\vartheta_{1}\) :

Fractal and fractional parameters

\(\frac{{{\rm d}^{{\tau_{1} ,\vartheta_{1} }} }}{{{\rm d}t^{{\tau_{1} ,\vartheta_{1} }} }}\) :

Fractal–fractional differential operator of Caputo–Fabrizio

\(\frac{{{\rm d}^{{\tau_{2} ,\vartheta_{2} }} }}{{{\rm d}t^{{\tau_{2} ,\vartheta_{2} }} }}\) :

Fractal–fractional differential operator of Atangana–Baleanu

β :

Thermal expansion coefficient

j :

Electric current density

σ:

Electric conductivity

t :

Time

αe :

Thermal diffusivity

ν:

Density of fluid

Ha:

Hartman number

References

  1. Lorenz EN. Deterministic non-periodic flow. J Atmos Sc. 1963;20(2):130–42.

    Article  Google Scholar 

  2. Oreper GM, Szekely J. The effect of a magnetic field on transport phenomena in a Bridgman-Stockbarger crystal growth. J Cryst Growth. 1984;67:405–19.

    Article  CAS  Google Scholar 

  3. Series RW, Hurle DTJ. The use of magnetic fields in semiconductor crystal growth. J Cryst Growth. 1991;113:305–28.

    Article  CAS  Google Scholar 

  4. Mahmuda MN, Hashim I. Effects of a magnetic field on chaotic convection in fluid layer heated from below. Int Commun Heat Mass Transfer. 2011;38:481–6.

    Article  Google Scholar 

  5. Kashif AA, Ilyas K, Gomez-Aguilar JF. Heat transfer in magnetohydrodynamic free convection flow of generalized ferrofluid with magnetite nanoparticles. J Thermal Anal Calorim. 2010;2:109. https://doi.org/10.1007/s10973-019-08992-1.

    Article  CAS  Google Scholar 

  6. Sushila SJ, Kumar D, Baleanu D. A hybrid analytical algorithm for thin film flow problem occurring in non-Newtonian fluid mechanics. Ain Shams Eng J. 2021;12:2297–302. https://doi.org/10.1016/j.asej.2020.09.006.

    Article  Google Scholar 

  7. Atangana A, Baleanu D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm Sci. 2016;20:763–9.

    Article  Google Scholar 

  8. Kashif AA, Ambreen S, Abdon A. Thermal stratification of rotational second-grade fluid through fractional differential operators. J Thermal Anal Calorim. 2020. https://doi.org/10.1007/s10973-020-09312-8.

    Article  Google Scholar 

  9. Caputo M, Fabrizio M. A new definition of fractional derivative without singular kernel. Prog Fract Differ Appl. 2015;1:1–13.

    Google Scholar 

  10. Abro KA, Ahmed Y. An analytic and mathematical synchronization of micropolar nanouid by Caputo-Fabrizio approach. Scientia Iranica Int J Sci Technol. 2019;26(6):3917–27. https://doi.org/10.24200/sci.2019.52437.2717.

    Article  Google Scholar 

  11. Mainardi F. Fractional calculus and waves in linear viscoelasticity: an introduction to mathematical models. London: Imperial College Press; 2010.

    Book  Google Scholar 

  12. Kashif AA, Ilyas K, Gomez-Aguilar. A mathematical analysis of a circular pipe in rate type fluid via Hankel transform. Eur Phys J Plus. 2018;133:397. https://doi.org/10.1140/epjp/i2018-12186-7.

    Article  CAS  Google Scholar 

  13. Abro KA, Ali AM, Anwer AM. Functionality of circuit via modern fractional differentiations. Analog Integr Circuits Signal Process Int J. 2019;99(1):11–21. https://doi.org/10.1007/s10470-018-1371-6.

    Article  Google Scholar 

  14. Gomez-Aguilar JF. Behavior characteristic of a cap-resistor, memcapacitor and a memristor from the response obtained of RC and RL electrical circuits described by fractional di_erential equations. Turk J Electr Eng Comput Sci. 2016;24(3):1421–33.

    Article  Google Scholar 

  15. Kashif AA, Anwar AM, Muhammad AU. A comparative mathematical analysis of RL and RC electrical circuits via Atangana-Baleanu and Caputo-Fabrizio fractional derivatives. Eur Phys J Plus. 2018;133:113. https://doi.org/10.1140/epjp/i2018-11953-8.

    Article  Google Scholar 

  16. Elwakil AS. Fractional-order circuits and systems: an emerging interdisciplinary research area. Circuits Syst Mag IEEE. 2010;10(4):40–50.

    Article  Google Scholar 

  17. Kashif AA, Jose FGA, Ilyas K, Nisar KS. Role of modern fractional derivatives in an armature-controlled DC servomotor. Eur Phys J Plus. 2019;134:553. https://doi.org/10.1140/epjp/i2019-12957-6.

    Article  Google Scholar 

  18. Kashif AA, Abdon A. Synchronization via fractal-fractional differential operators on two-mass torsional vibration system consisting of motor and roller. J Comput Nonlinear Dyn. 2021. https://doi.org/10.1115/1.4052189.

    Article  Google Scholar 

  19. Abdul S, Sohail A, Hamid K, Dumitru V. Solutions with Wright functions for time fractional convection flow near a heated vertical plate, Shakeel et al. Adv Differ Equ. 2016;2016:51. https://doi.org/10.1186/s13662-016-0775-9.

    Article  Google Scholar 

  20. Kashif AA, Abdon A. A computational technique for thermal analysis in coaxial cylinder of one-dimensional flow of fractional Oldroyd-B nanofluid. Int J Ambient Energy. 2021. https://doi.org/10.1080/01430750.2021.1939157.

    Article  Google Scholar 

  21. Hristov J. Steady-state heat conduction in a medium with spatial non-singular fading memory: derivation of Caputo-Fabrizio space-fractional derivative with Jeffrey’s kernel and analytical solutions. Therm Sci. 2017;21:827–39.

    Article  Google Scholar 

  22. Abro KA. A fractional and analytic investigation of thermo-diffusion process on free convection flow: an application to surface modification technology. Eur Phys J Plus. 2021. https://doi.org/10.1140/epjp/s13360-019-00046-7.

    Article  Google Scholar 

  23. Nadeem AS, Farhad A, Muhammad S, Ilyas K, Aftab AJ. A comparative study of Atangana-Baleanu and Caputo-Fabrizio fractional derivatives to the convective flow of a generalized Casson fluid. Eur Phys J Plus. 2017;132:54. https://doi.org/10.1140/epjp/i2017-11326-y.

    Article  CAS  Google Scholar 

  24. Kashif AA, Gomez-Aguilar JF. A comparison of heat and mass transfer on a Walter’s-B fluid via Caputo-Fabrizio versus Atangana-Baleanu fractional derivatives using the Fox-H function. Eur Phys J Plus. 2019;134:101. https://doi.org/10.1140/epjp/i2019-12507-4.

    Article  Google Scholar 

  25. Hammouch Z, Mekkaoui T. Control of a new chaotic fractional-order system using Mittag-Leffler stability. Nonlinear Stud. 2015;22:565–77.

    Google Scholar 

  26. Srivastava HM, Dubey VP, Kumar R, Singh J, Kumar D, Baleanu D. An efficient computational approach for a fractional-order biological population model with carrying capacity. Chaos Solitons Fractals. 2020;138:109880. https://doi.org/10.1016/j.chaos.2020.109880.

    Article  Google Scholar 

  27. Amanda R, Atangana A. Derivation of a groundwater flow model within leaky and self-similar aquifers: beyond Hantush model. Chaos Solitons Fractals. 2018;116:414–23.

    Article  Google Scholar 

  28. Singh J, Kumar S, Kumar D. A hybrid computational approach for Jeffery-Hamel flow in non-parallel walls. Neural Comput Appl. 2019. https://doi.org/10.1007/s00521-017-3198-y.

    Article  Google Scholar 

  29. Kashif AA, Abdon A. Strange attractors and optimal analysis of Chaotic Systems based on fractal-fractional differential operators. Int J Modell Simul. 2021;2:109. https://doi.org/10.1080/02286203.2021.1966729.

    Article  Google Scholar 

  30. Singh J, Kumar D, Kumar S. An efficient computational method for local fractional transport equation occurring in fractal porous media. Comput Appl Math. 2020;39:137. https://doi.org/10.1007/s40314-020-01162-2.

    Article  Google Scholar 

  31. Atangana A. Fractal-fractional differentiation and integration: connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals. 2017;102:396–406.

    Article  Google Scholar 

  32. Wen C, Hongguang S, **aodi Z, Dean K. Anomalous diffusion modeling by fractal and fractional derivatives. Comput Math Appl. 2010;59:1754–8.

    Article  Google Scholar 

  33. Yingjie L, Allen QY, Wen C, Rodolfo GG, Luis C, Thomas HM, Richard LM. A fractal derivative model for the characterization of anomalous diffusion in magnetic resonance imaging. Commun Nonlinear Sci Numer Simul. 2016;39:529–37.

    Article  Google Scholar 

  34. Wei C, Wen C, Wenxiang X. Characterizing the creep of viscoelastic materials by fractal derivative models. Int J Non-Linear Mech. 2016;87:58–63.

    Article  Google Scholar 

  35. Ilknur K. Modeling the heat flow equation with fractional-fractal differentiation. Chaos Solitons Fractals. 2019;128:83–91.

    Article  Google Scholar 

  36. Sania Q, Abdon A, Asif A. S, Strange chaotic attractors under fractal-fractional operators using newly proposed numerical methods. Eur Phys J Plus. 2019;134:523. https://doi.org/10.1140/epjp/i2019-13003-7.

    Article  CAS  Google Scholar 

  37. Kashif AA, Abdon A. A comparative study of convective fluid motion in rotating cavity via Atangana-Baleanu and Caputo-Fabrizio fractal–fractional differentiations. Eur Phys J Plus. 2020;135:226. https://doi.org/10.1140/epjp/s13360-020-00136-x.

    Article  CAS  Google Scholar 

  38. Hong GS, Zhipeng L, Yong Z, Wen C. Fractional and fractal derivative models for transient anomalous diffusion: model comparison. Chaos Solitons Fractals. 2017;102:346–53.

    Article  Google Scholar 

  39. Heydari MH. Numerical solution of nonlinear 2D optimal control problems generated by Atangana-Riemann-Liouville fractal-fractional derivative. Appl Numer Math. 2019. https://doi.org/10.1016/j.apnum.2019.10.020.

    Article  Google Scholar 

  40. Abro KA, Abdon A, Jose FG-A. An analytic study of bioheat transfer Pennes model via modern non-integers differential techniques. Eur Phys J Plus. 2021;136:1144. https://doi.org/10.1140/epjp/s13360-021-02136-x.

    Article  Google Scholar 

  41. Gomez-Aguilar JF. Chaos and multiple attractors in a fractal-fractional Shinriki’s oscillator model. Physica A. 2019. https://doi.org/10.1016/j.physa.2019.122918.

    Article  Google Scholar 

  42. Kashif AA, Mukarrum H, Mirza MB. An analytic study of molybdenum disulfide nanofluids using modern approach of Atangana-Baleanu fractional derivatives. Eur Phys J Plus. 2017;132:439. https://doi.org/10.1140/epjp/i2017-11689-y(2017).

    Article  Google Scholar 

  43. Ambreen S, Kashif AA, Muhammad AS. Thermodynamics of magnetohydrodynamic Brinkman fluid in porous medium: applications to thermal science. J Therm Anal Calorim. 2018. https://doi.org/10.1007/s10973-018-7897-0.

    Article  Google Scholar 

  44. Kashif AA, Ali DC, Irfan AA, Ilyas K. Dual thermal analysis of magnetohydrodynamic flow of nanofluids via modern approaches of Caputo-Fabrizio and Atangana-Baleanu fractional derivatives embedded in porous medium. J Thermal Anal Calorim. 2018;2:1–11. https://doi.org/10.1007/s10973-018-7302-z.

    Article  CAS  Google Scholar 

  45. Singh J, Jassim HK, Kumar D. An efficient computational technique for local fractional Fokker Planck equation. Physica A. 2020;555: 124525. https://doi.org/10.1016/j.physa.2020.124525.

    Article  Google Scholar 

  46. Giessler C, Sievert C, Krieger U, Halbedel B, Huelsenberg D, Luedke U, Thess A. A model for electromagnetic control of buoyancy driven convection in glass melts. FDMP Fluid Dyn Mater Process. 2005;1(3):247–66. https://doi.org/10.3970/fdmp.2005.001.247.

    Article  Google Scholar 

  47. Mechighel F, Armour N. Dost S Modeling of the effect of the presence of a free surface on transport structures and mixing during the dissolution process of silicon into germanium melt. J Therm Anal Calorim. 2021;146:61–91. https://doi.org/10.1007/s10973-020-09957-5.

    Article  CAS  Google Scholar 

  48. Mechighel F, El Ganaoui M, Kadja M, Pateyron B, Dost S. Numerical simulation of three dimensional low Prandtl liquid flow in a parallelepiped cavity under an external magnetic field. FDMP Fluid Dyn Mater Process. 2009;5(4):313–30. https://doi.org/10.3970/fdmp.2009.005.313.

    Article  Google Scholar 

  49. Mechighel F, Armour N, Dost S, Kadja M. Axisymmetric and 3-D numerical simulations of the effects of a static magnetic field on dissolution of silicon into germanium. CMES Comput Model Eng. 2014;97(1):53–80. https://doi.org/10.3970/cmes.2014.097.053.

    Article  Google Scholar 

Download references

Acknowledgements

The author Kashif Ali Abro is highly thankful and grateful to Mehran university of Engineering and Technology, Jamshoro, Pakistan, for generous support and facilities of this research work. José Francisco Gómez Aguilar acknowledges the support provided by CONACyT: cátedras CONACyT para jóvenes investigadores 2014 and SNI-CONACyT.

Author information

Authors and Affiliations

  1. Faculty of Natural and Agricultural Sciences, Institute of Ground Water Studies, University of the Free State, Bloemfontein, South Africa

    Kashif Ali Abro & Abdon Atangana

  2. Department of Basic Sciences and Related Studies, Mehran University of Engineering and Technology, Jamshoro, Pakistan

    Kashif Ali Abro

  3. CONACyT-Tecnológico Nacional de México/CENIDET. Interior Internado Palmira S/N, Col. Palmira, C.P. 62490, Cuernavaca, Morelos, México

    J. F. Gómez-Aguilar

  4. Department of Medical Research, China Medical University Hospital, China, Medical University, Taichung, Taiwan

    Abdon Atangana

Authors
  1. Kashif Ali Abro
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Abdon Atangana
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J. F. Gómez-Aguilar
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Kashif Ali Abro was involved in conceptualization, methodology, resources, formal analysis, writing-original draft, supervision; Abdon Atangana performed conceptualization, methodology, software, writing—original draft preparation; J.F. Gómez-Aguilar contributed to conceptualization, methodology, writing—review editing, validation, final draft preparation, and supervision.

Corresponding author

Correspondence to Kashif Ali Abro.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Abro, K.A., Atangana, A. & Gómez-Aguilar, J.F. Ferromagnetic Chaos in thermal convection of fluid through fractal–fractional differentiations. J Therm Anal Calorim 147, 8461–8473 (2022). https://doi.org/10.1007/s10973-021-11179-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10973-021-11179-2

Keywords

Search

Navigation