SpringerLink
Log in

A Unified \(L^2\) Norm Error Analysis of SAV-BDF Schemes for the Incompressible Navier–Stokes Equations

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

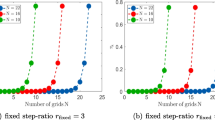
Abstract

This article is concerned with the \(L^2\) norm error analysis of high-order BDF methods for the incompressible Navier–Stokes equation subjected to no-slip boundary conditions. To mitigate the complexity of high-order time-step** algorithms caused by decoupling strategies, we combine the prediction–correction technique with a generalized scalar auxiliary variable approach to devise a family of linear, energy stable BDF schemes up to fifth-order accuracy in time. All the proposed schemes can be decoupled into a sequence of Poisson-type equations for the pressure and velocity fields, which significantly reduces the size of the linear systems at each time step. To deal with the essential difficulty raised by the non-A-stability of high-order BDF schemes, we introduce a class of discrete orthogonal convolution kernels to develop a unified framework for the \(L^2\) norm convergence analysis of the proposed high-order BDF schemes. The velocity attains optimal rate of convergence in the \(L^2\) norm under some mild mesh restrictions. Furthermore, building on the recent results concerning the positive definiteness of high-order BDF convolution kernels, we also provide an error estimate of the pressure in a weak \(L^2\) norm. Benchmark examples including the Taylor–Green vortex problem and the regularized lid-driven cavity flow with Reynolds numbers up to 5000 are included to verify the stability and high accuracy of our numerical schemes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (France)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Data Availability

Enquiries about data availability should be directed to the authors.

References

  1. An, R., Gao, H., Sun, W.: Optimal error analysis of Euler and Crank–Nicolson projection finite difference schemes for Landau–Lifshitz equation. SIAM J. Numer. Anal. 59, 1639–1662 (2021)

    Article  MathSciNet  Google Scholar 

  2. Archilla, B., Novo, J.: Robust error bounds for the Navier–Stokes equations using implicit–explicit second order BDF method with variable steps. IMA J. Numer. Anal. (2022). https://doi.org/10.1093/imanum/drad058

    Article  Google Scholar 

  3. Baker, A., Dougalis, V., Karakashian, O.: On a higher order accurate fully discrete Galerkin approximation to the Navier–Stokes equations. Math. Comput. 39, 339–375 (1982)

    Article  MathSciNet  Google Scholar 

  4. Boisneault, A., Dubuis, S., Picasso, M.: An adaptive space–time algorithm for the incompressible Navier–Stokes equations. J. Comput. Phys. 493, 112457 (2023)

    Article  MathSciNet  Google Scholar 

  5. Canuto, C., Hussaini, M., Quarteroni, A.: Spectral Methods in Fluid Dynamics. Springer, New York (2012)

    Google Scholar 

  6. DeCaria, V., Guzel, A., Layton, W., Li, Y.: A variable stepsize, variable order family of low complexity. SIAM J. Sci. Comput. 43, A2130–A2160 (2021)

    Article  MathSciNet  Google Scholar 

  7. DeCaria, V., Layton, W., Zhao, H.: A time-accurate, adaptive discretization for fluid flow problem. Int. J. Numer. Anal. Model. 17, 254–280 (2020)

    MathSciNet  Google Scholar 

  8. DeCaria, V., Schneier, M.: An embedded variable step IMEX scheme for the incompressible Navier–Stokes equations. Comput. Methods Appl. Mech. Eng. 376, 113661 (2021)

    Article  MathSciNet  Google Scholar 

  9. Emmrich, E.: Error of the two-step BDF for the incompressible Navier–Stokes problem. SAIM-Math. Model. Num. 38, 757–764 (2004)

    Article  MathSciNet  Google Scholar 

  10. Guermond, J., Shen, J.: A new class of truly consistent splitting schemes for incompressible flows. J. Comput. Phys. 192, 22 (2003)

    Article  MathSciNet  Google Scholar 

  11. Hairer, E., Wanner, G.: Solving Ordinary Differential Equation II. Springer, Berlin (2010)

    Google Scholar 

  12. Hay, A., Etienne, S., Pelletier, D., Garon, A.: hp-Adaptive time integration based on the BDF for viscous flows. J. Comput. Phys. 291, 151–176 (2015)

    Article  MathSciNet  Google Scholar 

  13. Huang, F., Shen, J.: Stability and error analysis of a class of high-order IMEX schemes for Navier–Stokes equations with periodic boundary conditions. SIAM J. Numer. Anal. 59, 2926–2954 (2021)

    Article  MathSciNet  Google Scholar 

  14. Huang, F., Shen, J.: A new class of implicit–explicit BDFk SAV schemes for general dissipative systems and their error analysis. Comput. Methods Appl. Mech. Eng. 392, 114718 (2022)

    Article  Google Scholar 

  15. Huang, F., Shen, J.: Stability and error analysis of a second-order consistent splitting scheme for the Navier–Stokes equations. SIAM J. Numer. Anal. 61, 2408–2433 (2023)

    Article  MathSciNet  Google Scholar 

  16. Kang, Y., Liao, H.-L.: Energy stability of BDF methods up to fifth-order for the molecular beam epitaxial model without slope selection. J. Sci. Comput. 91, 47 (2022). https://doi.org/10.1007/s10915-022-01830-x

    Article  MathSciNet  Google Scholar 

  17. Li, X., Shen, J.: Error analysis of the SAV-MAC scheme for the Navier–Stokes equations. SIAM J. Numer. Anal. 58, 2465–2491 (2020)

    Article  MathSciNet  Google Scholar 

  18. Li, X., Shen, J.: Error estimate of a consistent splitting GSAV scheme for the Navier–Stokes equations. Appl. Numer. Math. 188, 62–74 (2023)

    Article  MathSciNet  Google Scholar 

  19. Li, X., Shen, J., Liu, Z.: New SAV-pressure correction methods for the Navier–Stokes equations: stability and error analysis. Math. Comput. 91, 141–167 (2022)

    Article  MathSciNet  Google Scholar 

  20. Li, Z., Liao, H.-L.: Stability of variable-step BDF2 and BDF3 methods. SIAM J. Numer. Anal. 60, 2253–2272 (2022)

    Article  MathSciNet  Google Scholar 

  21. Liao, H.-L., Kang, Y.: \(\text{ L}^2\) norm error estimates of BDF methods up to fifth-order for the phase field crystal model. IMA J. Numer. Anal. (2023). https://doi.org/10.1093/imanum/drad047

    Article  Google Scholar 

  22. Liao, H.-L., Tang, T., Zhou, T.: A new discrete energy technique for multi-step backward difference formulas. CSIAM Trans. Appl. Math. 3, 318–334 (2022)

    Article  MathSciNet  Google Scholar 

  23. Liao, H.-L., Tang, T., Zhou, T.: Discrete energy analysis technique of the third-order variable-step BDF time-step** for diffusion equations. J. Comput. Math. 41, 325–344 (2023)

    Article  MathSciNet  Google Scholar 

  24. Liao, H.-L., Zhang, Z.: Analysis of adaptive BDF2 scheme for diffusion equations. Math. Comput. 90, 1207–1226 (2020)

    Article  MathSciNet  Google Scholar 

  25. Lin, L., Yang, Z., Dong, S.: Numerical approximation of incompressible Navier–Stokes equations based on an auxiliary energy variable. J. Comput. Phys. 388, 1–22 (2019)

    Article  MathSciNet  Google Scholar 

  26. Mortensen, M.: Shenfun: high performance spectral Galerkin computing platform. J. Open Source Softw. 3, 1071 (2018). https://doi.org/10.21105/joss.01071

    Article  Google Scholar 

  27. Shen, J.: Hopf bifurcation of the unsteady regularized driven cavity flow. J. Comput. Phys. 95, 228–245 (1991)

    Article  Google Scholar 

  28. Shen, J.: Efficient spectral-Galerkin method I. Direct solvers for second- and fourth-order equations by using Legendre polynomials. SIAM J. Sci. Comput. 15, 1489–1505 (1994)

    Article  MathSciNet  Google Scholar 

  29. Shen, J., Tang, T., Wang, L.: Spectral Methods: Algorithms, Analysis and Applications. Springer, Berlin (2011)

    Book  Google Scholar 

  30. Tabata, M., Uchiumi, S.: An exactly computable Lagrange–Galerkin scheme for the Navier–Stokes equations and its error estimates. Math. Comput. 87, 39–67 (2018)

    Article  MathSciNet  Google Scholar 

  31. Wu, K., Huang, F., Shen, J.: A new class of higher-order decoupled schemes for the incompressible Navier–Stokes equations and applications to rotating dynamics. J. Comput. Phys. 458, 111097 (2022)

    Article  MathSciNet  Google Scholar 

  32. Yan, Y., Hou, Y., Zhang, M.: Analysis of divergence-free \(\text{ H}^1\) conforming FEM with IMEX-SAV scheme for the Navier–Stokes equations at high Reynolds number. Math. Comput. 340, 557–582 (2023)

    Google Scholar 

Download references

Acknowledgements

The authors are very grateful to editor, anonymous referees for their invaluable comments and suggestions which have led to improvement of the paper.

Funding

Bingquan Ji is supported by Grants 2022TQ0046 and 2022M720019 from Postdoctoral Science Foundation of China. Hong-lin Liao is supported by a Grant 12071216 from National Natural Science Foundation of China.

Author information

Authors and Affiliations

  1. Institute of Applied Physics and Computational Mathematics, Bei**g, 100193, China

    Bingquan Ji

  2. School of Mathematics, Nan**g University of Aeronautics and Astronautics, Nan**g, 211106, China

    Hong-lin Liao

  3. Key Laboratory of Mathematical Modelling and High Performance Computing of Air Vehicles (NUAA), MIIT, Nan**g, 211106, China

    Hong-lin Liao

Authors
  1. Bingquan Ji
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hong-lin Liao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hong-lin Liao.

Ethics declarations

Conflict of interest

The authors have not disclosed any competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ji, B., Liao, Hl. A Unified \(L^2\) Norm Error Analysis of SAV-BDF Schemes for the Incompressible Navier–Stokes Equations. J Sci Comput 100, 5 (2024). https://doi.org/10.1007/s10915-024-02555-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-024-02555-9

Keywords

Mathematics Subject Classification

Search

Navigation