1 Introduction

In the automotive body assemblies, RSW is often used [1,2,3], and its fatigue analysis is of paramount importance for ensuring safety. The most common testing method for the fatigue strength of RSW joints is the tensile-shear fatigue test. This method requires recording the number of cycles until crack initiation under different conditions such as plate thickness, plate width, nugget diameter, and applied loads. The collected data points are then utilized to construct the fatigue curve, the relationship between the applied force (F) and fatigue cycles (N), which follows a power-law mathematical equation under specific experimental conditions [4,5,6,7,8]. Although this method accurately predicts the number of cycles to failure under different loading conditions, it incurs significant time and material costs.

To achieve efficient predictions while saving time and material resources, it is necessary to introduce the concept of fracture mechanics. In 1968, Rice [9] introduced the concept of J-integral, which is a line integral displayed in a two-dimensional stress/strain field of elastic or elastoplastic materials. This J-integral is path-independent and solely dependent on the rate of energy release. However, its theoretical application of is limited to two-dimensional problems, whereas fatigue failure in RSW joints involves three-dimensional crack propagation. Subsequent studies have proposed various methods for calculating the stress intensity factor (SIF), the K value, in RSW, taking into account different materials and crack geometries [10,11,12]. Same, calculating K values based on ideal linear formulas still has limitations. In addition, extracting the stress necessary to calculate the SIF for a specific point in a three-dimension model is challenging. To overcome these problems, Saito validated the accuracy of the Characteristic Tensor Method (CTM) in assessing three-dimensional stress singularities in 2021 [13]. Relying on this method, the stress values in the spherical region at the crack tip are selected for integral calculation and then the SIF value can be obtained when the integration region’s size approaches zero [13]. Subsequently, based on a collaborative study between automobile manufacturers and steel makers [14], it was found that the coefficient of the applied force and fatigue cycles (F-N curve) for RSW joints is related to the thickness and width of two plates and is less affected by material properties for high-strength steels. From the local view, the fatigue cracking life (N) is determined by the stress intensity factor SIF in the RSW joints. In other words, the curve between SIF and fatigue cracking cycles N can be a general curve which can then be transformed to the global F-N curve of RSW joints under arbitrary testing conditions. Here, the SIF-N curve is called as the master curve (MC) for fatigue life evaluation. Therefore, to create the SIF-N curve and its validation by limited numbers of experimental F-N curves become necessary.

Although the SIF-N curve represents the mechanism of fatigue failure, automobile companies must establish the database expressed by the F-N curves of RSW joints with various specified dimensions for extended applications from various local approaches. Considering this need for automotive industries, the prediction method of F-N curve from SIF-N curve must be developed and then extended to various plate thickness combinations and widths as well as nugget diameters of RSW joints of high-strength steels with the aid of finite elements method (FEM) and ML. Furthermore, the FE analyzed results revealed a linear correlation between the local SIF and global applied force. Based on validated FEM results and their datasets, a ML approach is introduced to generalize the local SIF-N curve to global F-N fatigue curve by calculating scale factors. ML methods, based on artificial intelligence and data analysis techniques, have shown tremendous potential in accurately predicting the fatigue behavior of various materials and structures [15,16,17,18]. Their primary advantage in fatigue prediction lies in their ability to handle the nonlinear and complex relationships between input variables and fatigue life. Traditional analytical models often rely on simplified assumptions and linear relationships, which may fail to capture the intricate nature of fatigue behavior. Among ML methods, the backpropagation (BP) neural network has emerged as a widely adopted option for nonlinear fitting in ML [19, 20]. As highlighted by Li et al. in 2012, The BP Backpropagation neural network does not require specific mathematical formulas to calculate the relationship between variables. Instead, it learns from the input–output patterns of the training data through an iterative process. The network adjusts its internal weights and biases to minimize the error between the predicted output and the actual output [20]. By establishing the aforementioned models, it becomes possible to predict the trend of the F-N curve. Finally, the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm is employed to optimize the exponent alpha of the power law model, resulting in improved model fitting to experimental data. The BFGS algorithm serves as an extremum-finding tool in this process. Compared with other similar algorithms such as the Newton method and quasi-Newton method, the BFGS algorithm demonstrates superior performance in terms of fast and global convergence [21, 22].

In this study, a prediction model was successfully developed by integrating FEA, experimentation, and ML-based fitting techniques. This model enables the quick calculation of a power function F-N curve under the various magnitudes of plate thickness, plate width and welding nugget diameter. Compared to previous approaches that rely solely on ML models for prediction, this method used the localized parameter of stress intensity factor based on the fracture mechanics. By incorporating insights from fracture mechanics, it enhances the accuracy of the ML results, even with a limited amount of data. The effectiveness of this model was demonstrated by comparing its results with the experimental and literature data.

2 Methodology

2.1 Preparation of tensile-shear fatigue test pieces

The test involves welding specimens comprising two high-strength steel plates. DP590-DP980 are under standard Q/BQB 418–2009 (standard of Baoshan Iron&Steel Co.,Ltd.,China), and 1300 T is under standard VDA-239 100 (standard of German Association of the Automotive Industry). The most important reason for selecting these kinds of steel is their extensive use in the automotive industry. The primary objective of this study is to provide practical methods for automotive manufacturers to reduce the number of fatigue tests while accurately assessing RSW components involved in assembly. These steels have been chosen to meet the requirements of the production application. The chemical composition of the steel is shown in Table 1.

Table 1 Chemical element of steel
Full size table

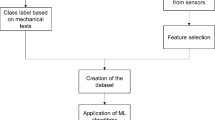
Based on the plate thickness and width, a current range of 7kA-8kA is selected, while a force of 3kN-5kN is applied at both ends. The welding electrode diameter is 8 mm, and the welding time is set between 350 and 500 ms. The selection of these parameters is based on previous experience [23], which can completely form the nugget diameter size required by the ISO 14324–2003 standard. For the fatigue performance of high-strength steel RSW joints, the size of the nugget diameter is a critical factor [14]. It is also an important parameter in prediction model. Following that, the test pieces are labeled and categorized according to various parameters such as material type, thickness, and width, to facilitate subsequent experimental procedures (Fig. 1).

Fig. 1
figure 1

Test material (a) pre-welding and (b) post-welding, (c) (1) Weld nugget, (2) Heat affected zone, (3) Corona bond, (4) Base metal, (5) Sheet separation, (6) Inter-expulsion, (7) Indentation, (d) Side view of RSW joint

Full size image

2.2 Tensile-shear fatigue testing

The tensile-shear fatigue test is conducted in accordance with the ISO 14324–2003 standard. Table 2 presents the physical properties of the experimental materials.

Table 2 Mechanical properties (DP steel under standard Q/BQB 418–2009, TRIP steel under standard VDA-239 100)
Full size table

As shown in Fig. 2 (a), (b) and (c), the test piece comprises two plates of equal width, with the weld nugget area located in the middle of the intersection area of the two plates.

Fig. 2
figure 2

(a) Top view of the test piece, (b) Force direction in the tensile-shear fatigue test, (c) Diagram of force loading, (d) Side view after fatigue test, (e) Cross-section at the end of fatigue test

Full size image

Before the fatigue tests, some test conditions such as grinding treatment, humidity, temperature, and the crosshead speed [24,25,26] need to be carefully considered or controlled. The experiment was conducted at a relative humidity of 45% to 65% and a temperature range of 5 to 20 degrees Celsius. Additionally, the frequency of the applied force at the ends of the crosshead was set at a fixed 60 Hz, as shown in Fig. 2 (c). The reason for choosing a fixed frequency instead of a fixed speed is mainly because the physical dimensions of the specimens used in the test varies greatly. It is difficult to fix the amplitude of the force by the fixed speed. When the test begins, the lower end of the test piece is held in place and a sinusoidally varying force [N] perpendicular to the ground is applied to the upper end. The maximum force is recorded as Max F, while the minimum force is 100N. The test is continued until cracks can be observed from the surface. At this point fatigue failure is considered to have occurred and the number of tension cycles is recorded as the number of cycles to failure \({N}_{f}\). During testing, the test pieces have obvious bending deformation and the gap opening between two plates as shown in Fig. 2(d). After the welding, the plate was cut along the length direction using a wire cutting method from the center as shown in Fig. 2(a). Then, the cut specimens were finely polished using sandpaper. Finally, the specimens were photographed using a low-magnification lens. The cross section is observed to confirm that cracks have initialized in one or both plates as a basis for fatigue damage, as shown in Fig. 2 (e).

For example, DP590 and DP980 were used in this study. The width “W” of two plates is 38 mm. The plates had a thickness “T” of 1.4 mm, while the diameters of the weld nuggets were “D” which are 6.0 mm and 5.7 mm, respectively. In a total of 8 groups of experiment, the position of crack initiation and the number of cycles at which it occurred were recorded for each experiment. These results are presented in Fig. 3:

Fig. 3
figure 3

(a) Top view of crack initialization and propagation of DP590 test pieces with T = 1.4 mm, D = 6 mm, and W = 38 mm, (b) Top view of crack initialization and propagation of DP980 test pieces with T = 1.4 mm, D = 5.7 mm, and W = 38 mm

Full size image

The observation of the experimental phenomena revealed that for the tensile-shear fatigue test of high-strength steels, the crack initiates from one point at the edge of weld nugget and then expands towards the edges of two plates. This phenomenon is less influenced by the material properties of high-strength steels [14]. Then, according to ISO14324-2003 standard, the amplitude of the force applied at both ends is recorded as \(\Delta F\) (Table 3, Fig. 4):

Table 3 Datasets of tensile-shear fatigue test
Full size table
Fig. 4
figure 4

F-N Curve of DP590 (Thickness = 1.4 mm, Diameter = 6 mm, Width = 38 mm) and DP980 (Thickness = 1.4 mm, Diameter = 5.7 mm, Width = 38 mm)

Full size image
$$\Delta F=\frac{Max F-Min F}{2}$$
(1)

In addition to the 8 groups of tests mentioned above, DP590 material was selected with the sheet thickness of 1.0 mm-1.8 mm, nugget diameter of 5.0 mm—6.8 mm and width of 20.0 – 76.0 mm for a total of 34 groups. The physical dimensions of the test piece are shown in Fig. 5. There are also different combinations of DP780, 1300 T in the same experimental conditions within the range of values for a total of 70 groups. The total experimental data is 104 groups. The amplitude forces are 1950N, 1450N, 950N and 700N for each RSW joints, and the number of cycles is within 1.0E + 7 which is treated as the fatigue limit.

Fig. 5
figure 5

Physical dimensions of test specimen

Full size image

2.3 Calculation of stress intensity factors

In 2022, the Ma team measured the hardness of DP980 RSW joint specimens. These specimens had dimensions of 125 mm in length, 38 mm in width, 1.2 mm in thickness, and a nugget diameter of 6 mm [23]. The DP980 material used in previous study was sourced from the same standard as the current study and had identical physical dimensions.

Furthermore, the Ma team investigated the microstructure of DP980 RSW joints. As illustrated in Fig. 6, the UCHAZ exhibited higher hardness values compared to other regions. Figure 7 presents the hardness distribution along the length direction L1 of the specimen, which was similar to the measurements obtained in current experiment, as shown in Fig. 8. Cracks initiated from the notch (separation of two plates) at the UCHAZ, propagated through the martensite formation region, and eventually extended to the surface of the plate. Additionally, Fig. 6(c) depicts the fully martensitic structure observed in the UCHAZ, which possesses lower fracture toughness, facilitating easier fatigue crack propagation. This measured hardness distribution indirectly supports the observed crack mode in Fig. 8.

Fig. 6
figure 6

The Scanning Electron Microscope (SEM) image of microstructure in (a) base metal (BM), (b) weld nugget, (c) upper-critical heat affected zone (UCHAZ) and (d) subcritical affected zone (SCHAZ) (e) Hardness distribution

Full size image
Fig. 7
figure 7

Hardness variation along with L1

Full size image
Fig. 8
figure 8

Crack initiation modes for different sizes and loads of test pieces

Full size image

In this study, the SIF is calculated using an elastic FEA model based on fracture mechanics principles. Specifically, the Characteristic Tensor Method (CTM) is employed for this purpose. In 2021, Saito proposed and verified the accuracy of CTM for evaluating three-dimensional stress singularity [13]. This method is simple in addressing three-dimensional crack problems. Building on this work, the relationship between CT and SIF calculated from the stress distribution around the crack tip was derived. As depicted in Figs. 1(c) and 2(e), the crack initiation typically occurs at the edge of nugget of the RSW joint during the tensile-shear fatigue test. If the nugget edge is approximately treated as the crack tip, its SIF as a local approach to fatigue phenomena can be calculated using the simple CTM as shown in Fig. 9.

Fig. 9
figure 9

Method of calculating SIF by CTM in RSW Model

Full size image

To calculate the SIF, which is also expressed by the symbol ΔK, at the nugget edge using CMT [13], the averaged stress “\({\mu }_{av}\)” in the spherical domain “\({\Omega }_{R}\)” is computed firstly,

$${\mu }_{\mathrm{av}}=\frac{1}{{V}_{{\Omega }_{R}}}{\int }_{{\Omega }_{R}}{\sigma }_{\mathrm{ij}}dV$$
(2)

Here, “V” means volume, \({\sigma }_{\mathrm{ij}}\) represents the stress tensor in six directions. The average stress “\({\hat{\mu }}_{\mathrm{av}}\)” within the spherical region of the finite volume of the selected mesh in the FE analysis is then defined [13]:

$${\hat{\mu }}_{\mathrm{av}}\left(X,R\right)=\frac{1}{{\hat{V}}_{\Omega R}}\sum\nolimits_{\mathrm{z}=1}^{{\mathrm{n}}_{\mathrm{z}}}{\left({\sigma }_{\mathrm{ij}}detJ\right)}_{\mathrm{z}}{\mathrm{W}}_{\mathrm{z}}$$
(3)

Here, “X” is the center of spherical region, “R” is radius. “\({\hat{V}}_{\Omega R}"\) is the volume calculated by the Gaussian quadrature. \("n"\) means the number of points is selected in spherical area. \("detJ"\) is Jacobian where “\(W\)” is the weight of Gaussian quadrature. Now for the point “X” on one at the tip of the crack, the SIF is calculated as follows [13]:

$$\Delta K\left(\mathrm{X}\right)=\frac{5}{3}\frac{\sqrt{\left({\left.2\pi \right)}^{3}\right.}R}{{4.8\mathrm{c}}_{\theta }}{\hat{\mu }}_{\mathrm{av}}\left(X,R\right)\left(R\to 0\right)$$
(4)

where “\(\theta\)” is the angle shown in Fig. 9, “\({\mathrm{c}}_{\theta }\)” is a constant [13]:

$${\mathrm{c}}_{\theta }={\int }_{0}^{\pi }\sqrt{\mathrm{si}n\theta } d\theta$$
(5)

In the above approach, the SIF at the tip of crack is estimated by taking the average stress value in the spherical region of the crack tip calculated by FEM. Furthermore, Saito's article demonstrates that mesh size divisions between 0.01 mm and 0.025 mm have little effect on the “\(\Delta K\)” value when using the FEM for this calculation. Likewise, the ratio of “R” to crack length “c” (R/c) between 0 and 0.1 has little effect on the calculated results [13]. In later calculations, a mesh size of 0.1 mm and an R/c of 0.5 are chosen.

3 F-N curve prediction methods

3.1 Flow chart and master curve for F-N curve prediction

The flow of the prediction methods for F-N curve is shown in Fig. 10.

Fig. 10
figure 10

Flow chart for F-N curve prediction

Full size image

First, the F-N curves were obtained under one experimental condition and formulated by following equation:

$$\Delta F=m{N}_{f}^{\alpha }$$
(6)

Here, “m” is the coefficient of fatigue curve, and “α” is its power. \({N}_{f}\) represents number of cycles to fatigue failure. FEA was performed according to the current experimental conditions. It is generally considered that the SIF value in the stress concentration region is larger than the other regions, and the FE analyzed SIF value (ΔK) divided by the loading force ΔF is extracted and defined as the master curve coefficient \({C}_{mc}\):

$${C}_{mc}=(max\Delta K/\Delta F{)}_{FEA}$$
(7)

\({C}_{kf}\) is set proportional to the fatigue curve coefficient m, and they have the same base unit. Then the relationship between the \({C}_{kf}\) and \({C}_{mc}\) can be assumed as:

$${C}_{kf}=m\beta {C}_{mc}$$
(8)

Here \(\beta {C}_{mc}\) is a constant, and \(\beta\) is a hypothetical number with the same base unit as \({C}_{mc}^{-1}\). Then, a F-N relationship base on \({C}_{mc}\) can be established:

$$\Delta F={C}_{kf}/{{C}_{mc}\times N}_{f}^{\alpha }$$
(9)

Based on this hypothetical relationship, if the experimental conditions are changed, the new fatigue curve can be written as:

$$\Delta F=({C}_{kf}{)}_{new}/{({C}_{mc}{)}_{new}\times N}_{f}^{\alpha }$$
(10)

\(\beta\) plays as a scaling factor and is able to incorporate the results of the FEA \({C}_{mc}\) to the calculation process of the predicted experimental results. Using Eqs. (9) and (10) it is possible to extend the local SIF obtained by FEA to the global fatigue curve coefficient calculation. Meanwhile, by completing the quantification of the relationship between \({C}_{kf}\), \({C}_{mc}\) and experimental conditions, it is possible to achieve predictions of \({N}_{f}\) by applying different force \(\Delta F\).

In the case of DP980, the distribution of stress is shown in Fig. 11(a). The distribution of \({C}_{mc}\) near the nugget area is presented in Fig. 11(b), with a maximum value of 5.11 mm−1.5. Considering the linear relationship between \(\Delta K\) and \(\Delta F\) analyzed by FEM, the force is here fixed to 10kN for the \({C}_{mc}\) calculation. The \({C}_{mc}\) for different plate thicknesses, widths, and nugget diameters are shown in Table 4.

Fig. 11
figure 11

(a) stress distribution in FE methods, (b) \({C}_{mc}\) distribution on y direction from nugget center

Full size image
Table 4 \({C}_{mc}\) obtained by FEA under different experimental conditions
Full size table

3.2 Linear regression method for F-N curve prediction

Through these data, the least square method is utilized to perform linear regression analysis of the relationship between the different combinations of experimental conditions and \({C}_{mc}\). This is conducted to the linear relationship among the thickness of the thinner plate \({t}_{min}\), the thicker plate \({t}_{max}\), and the diameter of the weld nugget D with \({C}_{mc}\) when W = 38 mm.

$${C}_{mc}={A}_{1}+{A}_{2}{t}_{min}+{A}_{3}{t}_{max}+{A}_{4}D$$
(11)

Here, A1, A2, A3 and A4 are constant. However, no linear relationship was observed between the width of the sheet and \({C}_{mc}\). To determine the relationship of \({C}_{mcW}\) between width W and \({C}_{mc}\), FEA was conducted for plate widths of 20 mm, 30 mm, 36 mm, and 76 mm, along a plate thickness of 1.4 mm and a weld nugget diameter of 6.1 mm, as illustrated in Fig. 12. Through analysis, it was found that a correlation between \({C}_{mc}\) and the plate width W exists, which is:

Fig. 12
figure 12

Stress distribution and \({C}_{mc}\) of four different widths W with the same thickness and diameter of nugget

Full size image
$${C}_{mcW}={B}_{1}{W}^{{B}_{2}}$$
(12)

Here, B1 and B2 are constant.

A linear relationship between \({C}_{mc}\) and test conditions can be expressed through Eqs. (11) and (12):

$${C}_{mc}=exp\{\mathrm{ln}({A}_{1}+{A}_{2}{t}_{min}+{A}_{3}{t}_{max}+{A}_{4}D)+[{B}_{2}\mathrm{ln}(\frac{{W}_{ref}}{W})]\}$$
(13)
$${\text{Error }}^{2}=\frac{1}{2}\sum {{C}_{mc}-{({C}_{mc})}_{i}]}^{2}$$
(14)

Here, \({({C}_{mc})}_{i}\) is the results of FE methods calculation. The reference width, denoted as \({W}_{ref}\), is typically set to 38 mm. It serves as a constant reference value in the Eq. (13) to account for experimental data obtained from plates with widths different from 38 mm. By incorporating this reference width, the equation can be linearized to accurately represent the relationship between the experimental data and the corresponding plate widths. In Table 4, the total numbers of data in this study “i” is equal to 33. Here, a total of 28 sets of data with a plate width W of 38 mm are selected, and the values of coefficients A1, A2, A3 and A4 are calculated using the least square method to minimize error:

$$\frac{\partial Error}{\partial {A}_{1}}=\sum\nolimits_{i=1}^{33}[{C}_{mc}({A}_{2})-{({C}_{mc})}_{i}]$$
(15)
$$\frac{\partial \, Error \, }{\partial {A}_{2}}=\sum\nolimits_{i=1}^{33}[{C}_{mc}({A}_{2})-{({C}_{mc})}_{i}]{t}_{min}$$
(16)
$$\frac{\partial \, Error \, }{\partial {A}_{3}}=\sum\nolimits_{i=1}^{33}[{C}_{mc}({A}_{3})-{({C}_{mc})}_{i}]{t}_{max}$$
(17)
$$\frac{\partial Error}{\partial {A}_{4}}=\sum\nolimits_{i=1}^{33}[{C}_{mc}({A}_{4})-{({C}_{mc})}_{i}]D$$
(18)

The matrix is constructed from the results of partial derivatives:

$$\left|\begin{array}{c}\frac{\partial Error}{\partial {A}_{1}}\\ \frac{\partial Error}{\partial {A}_{2}}\\ \frac{\partial Error}{\partial {A}_{3}}\\ \frac{\partial Error}{\partial {A}_{4}}\end{array}\right|\times \left|\begin{array}{c}{A}_{1}\\ {A}_{2}\\ {A}_{3}\\ {A}_{4}\end{array}\right|=\left|\begin{array}{c}({C}_{mc}{)}_{1}\\ ({C}_{mc}{)}_{2}\\ ({C}_{mc}{)}_{3}\\ \dots \\ ({C}_{mc}{)}_{33}\end{array}\right|$$
(19)

The values of A1, A2, A3, and A4 are obtained by solving the matrix in Eq. (19). In addition, the value of B2 in Eq. (12) is obtained by linear fitting for the four groups of other conditions that are the same, but the plate width is different. The result can be calculated exponentially:

$${C}_{mc}=exp\{\mathrm{ln}(10.146-3.107{t}_{min}+0.889{t}_{max}-0.338D)+[0.3811\text{ ln }(\frac{38}{W})]\}$$
(20)

Figure 13 (a) illustrates that the linear regression method implemented to compute \({C}_{mc}\) yields mostly precise outcomes. When trying to calculate \({C}_{kf}\) using the same method in combination with experimental data, a relationship as in Eq. (21) was obtained, and the value of \({C}_{kf}\) was found to have little relationship with the plate width after bringing in \({C}_{mc}\). As shown in Fig. 13(b), at least 27 of the 104 data sets were found not to meet the expected criteria in the description of the mathematical formulation method:

Fig. 13
figure 13

Compare linear regression results of (a) \({C}_{mc}\) with results of FE methods, (b) \({C}_{kf}\) with experiments

Full size image
$${C}_{kf}=350101.055+22283.395{t}_{min}+85499.209{t}_{max}-35705.281D$$
(21)

Therefore, a nonlinear fitting method is needed to find the relationship between \({C}_{kf}\) and experimental conditions. ML can meet this requirement.

3.3 BP Neural Network Design for F-N curve prediction

In Sections 3.1 and 3.2, fracture mechanics equations, finite element calculations, and the least squares method were utilized to obtain the \({C}_{mc}\) and its linear fitting equation. Additionally, we established the basic approach of using \({C}_{kf}/{C}_{mc}\) to predict fatigue curve coefficients. However, during this process, it was discovered that \({C}_{kf}\) could not be accurately represented by linear fitting. Therefore, a nonlinear relationship was required to accurately describe the relationship between macroscopic experimental conditions and \({C}_{kf}\). ML methods are well-suited for handling nonlinear fitting tasks. It is worth noting that \({C}_{kf}\) is obtained from \({C}_{mc}\) using Eq. (8). Both \({C}_{kf}\) and \({C}_{mc}\) are correlated with macroscopic experimental conditions such as the thickness, width, and diameter of the nugget of the plates. This correlation helps alleviate the limitations of a small database size. In this case, several popular algorithm structures can be considered, including decision trees, random forests, support vector machines, and BP neural networks. Due to the inherent randomness of predictions made using ML methods, and the lack of a standardized approach for training models on databases of different sizes, researchers often rely on their own experience when selecting training methods. Through literature, it has been observed that neural networks tend to outperform other methods in terms of goodness of fit and prediction accuracy, especially when there is enough data for training [27,28,29]. Based on the experiences reported in these studies, the method of choice was the BP neural network.

Considering the significant time and material requirements for tensile-shear fatigue tests, it is impractical to supplement the data with thousands of samples for neural network training. Drawing inspiration from the methods used in references [27,28,29], data augmentation can be achieved by interpolating data points based on the physical characteristics observed in the experimental data. As mentioned earlier, for a given physical dimension of the specimen, the relationship between ΔF and fatigue life \({N}_{f}\) follows a power-law curve. To expand the dataset, 12 sets of 4 fatigue test data points, corresponding to different physical dimensions, are selected as shown in Table 5. Around these data points, a normal distribution is generated within a 10% error range to produce an additional 384 data points. As depicted in Fig. 14, the augmented dataset for training is expanded to a total of 444 data points. These data points exhibit distinct features that reflect the physical dimensions of the specimen and fatigue life. Then, the input variables x1 and x2 represent thickness of plates, x3 is the diameter of nugget as shown in Fig. 15. Here, “w” is a weight defined by the algorithm, and the relationship "y" as follows [29]:

Table 5 Data groups and physical dimensions
Full size table
Fig. 14
figure 14

Different groups of experimental data and generated data

Full size image
Fig. 15
figure 15

Structure of BP neural network regression algorithm

Full size image
$$y=f({w}^{T}x)$$
(22)

For the backpropagation process, define the error value:

$$E=\frac{1}{2}(t-y{)}^{2}$$
(23)

Here, "t" is the value of \({C}_{kf}\) calculated from the experimental data based on the FEA. Then we define the relationship between weight w and error E as:

$$\Delta w=-\eta {E}^{\mathrm{^{\prime}}}$$
(24)

Here, “\(\eta\)” is a proportional coefficient of an irrational number. Based on the above formula, using the Delta learning method, we can deduce the mathematical formula:

$$\frac{\partial E}{\partial w}=\frac{\partial }{2\partial w}{[t-f({w}^{T}x)]}^{2}$$
(25)
$$\frac{\partial E}{\partial w}=-(t-y){f}^{\mathrm{^{\prime}}}({w}^{T}x)x$$
(26)
$$\Delta w=\eta (t-y){f}^{\mathrm{^{\prime}}}({w}^{T}x)x$$
(27)

The main purpose of the BP neural network is to modify the weights to minimize the error value. The Delta learning rule is a general learning rule in ML that uses gradient descent. Based on the above-mentioned basic method, we can build a fully connected layer gradient structure as shown in Fig. 15.

3.4 BFGS Algorithm Optimize for F-N curve prediction

The Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm is a numerical optimization algorithm for solving unconstrained nonlinear optimization problems which is suitable for optimize “α” value. It is widely used to find the extreme points of functions [21].

First, the error sum between the prediction model and the experimental data can be defined as the variable "q".

The basic idea of the BFGS algorithm is to gradually improve the search direction by continuously updating the approximate Hessian matrix. In each iteration, the BFGS algorithm determines the position of the next step according to the current search direction and step size, and calculates the gradient of the position and the approximate Hessian matrix. Then, by using this information to update the approximate Hessian matrix to better estimate the curvature of the objective function, it can reduce the cost of computing the Hessian matrix compared to other method like Newton's method [22].

To initiate the optimization process, the error sum between the prediction model and the experimental data can be defined as the variable "q". This error sum, or objective function, quantifies the discrepancy between the predicted values obtained from the model and the corresponding experimental data points [21]:

$${C}_{n}={({C}_{kf}/{C}_{mc})}_{n}$$
(28)
$$q(\mathrm{\alpha })={\sum }_{1}^{n}{[{C}_{n}\times {\left({N}_{f}\right)}_{\mathrm{exp}n}^{\alpha }-{F}_{\mathrm{exp}n}]}^{2}$$
(29)

Here “n” is the number of experimental data.

Then use mathematical formulas to express the operation process of BFGS algorithm:

$${q}^{k}={B}_{k+1}{p}^{k}$$
(30)
$${H}_{K+1}={B}_{k+1}^{-1}$$
(31)
$${B}_{k+1}={B}_{k}+\frac{{q}^{k}{q}^{(k)T}}{{q}^{(k)T}{p}^{k}}-\frac{{B}_{k}{p}^{k}{p}^{(k)T}{B}_{k}}{{p}^{(k)T}{B}_{k}{p}^{k}}$$
(32)
$${H}_{k+1}^{BFGS}={H}_{K}+(1+\frac{{q}^{(k)T}{H}_{k}{q}^{k}}{{p}^{(k)T}{q}^{k}})\frac{{p}^{(k)T}{q}^{k}}{{p}^{(k)T}{q}^{k}}-\frac{{p}^{k}{q}^{(k)T}{H}_{k}+{H}_{k}{q}^{k}{p}^{(k)T}}{{p}^{(k)T}{q}^{k}}$$
(33)

Here, “k” is step value which \({H}_{k}\) is Hessian matrix, \({B}_{k}\) is the inverse matrix of \({H}_{k}\). “q” is the matrix from the formula \(q(\mathrm{\alpha })\), while the assumed matrix “p” preserves the information after multiplying the matrix “q” with the Hessian matrix as shown in Eq. (28).

\({H}_{k+1}^{BFGS}\) represents the process of each step of \({H}_{k}\) updating. If \(q(\mathrm{\alpha })\) is used to express a continuous function in the domain of definition, and the second-order partial derivative of this function always exists then we can use BFGS algorithm to optimize. The structure of the error minimum solution process is shown in Fig. 16:

Fig. 16
figure 16

BFGS algorithm structure

Full size image

Observing the pattern of crack generation and development, in the experiment, it is seen that cracks are usually generated on the thinner side of the plate. If the difference of tensile strength of the two plates is around 300–700 MPa, cracks will still develop on the thinner one, regardless of whether this one plate is stronger than the other one. In this process, the stronger tensile strength delays the number of cycles in which cracks occur. As a result of this phenomenon, as shown in Fig. 17 (in [mm]), the fixed value of "α" is -0.32, at which point the error of the model is about 20% of the experimental value. For this case, the BFGS algorithm is used to optimize all predicted values that exhibit an error of more than 20% of the initial value. This is shown in Fig. 17. A tolerance value of 106 was set. The initial value was determined to be -0.32. After optimization the ML model using the BFGS algorithm, the model was able to adjust the value of "α" according to the difference in the tensile strength of the two plates. This resulted in a better fit of the predicted curve to the experimental data.

Fig. 17
figure 17

Results after BFGS optimization

Full size image

4 Results and discussions

4.1 Predicted results comparisons by experimental results and discussions

After the ML model training outlined, a trained model can be obtained. This model is capable of performing regressions on \({C}_{kf}\), using different input experimental conditions, and thereafter predicting the power function model of the F-N curve. The BFGS algorithm is subsequently applied to further enhance the accuracy of the predictive model. Figure 18 (a), (b) presents a comparison between the results of the ML model and eight sets of data with distinct experimental conditions, indicating a positive correlation between the trend of the predicted outcomes and the actual results.

Fig. 18
figure 18

Prediction results of (a) DP590 and DP780, (b) 1300 T and DP980

Full size image

Furthermore, a comparison was made between the F-N curve and the data recorded in reference [5]. Following the standard of RSW tensile-shear fatigue test GB/T 15111–94, which provides a definition for the fatigue failure state where the crack length equals the nugget diameter [5]. Under this definition, the fatigue test stops after surface cracks appear and are observed, similar to the definition of fatigue failure in ISO 14324–2003 standard used in the text. The calculated results were converted from amplitude applied load to the predicted results of maximum applied load depend on Eq. (1). As depicted in Fig. 19, the predicted results continue to demonstrate good accuracy. However, the cross-validation of fatigue data for 6061-T6 aluminum alloy [30] demonstrated poor performance of the model based on the data of high strength steel when applied to aluminum alloys. The first reason is that the loading frequency was set at 10 Hz in the literature [30], which is significantly different from the 60 Hz used in this study. Secondly, from the perspective of fracture mechanics, SIF has three modes (KI, KII, KIII), it is difficult to directly use data of high-strength steels to aluminum alloys. In the future, discussing the commonality of SIF for different materials and different structures and extending it to the field of machine learning is a wonderful research direction.

Fig. 19
figure 19

Cross-check for (a) B1500HS and M190

Full size image

Overall, taking all of the \({N}_{f}\) of the experimental data in datasets (total number is 104) as the x-axis and the \({N}_{f}\) of the predicted results as the y-axis, the data is divided into training and testing. Due to the extremely high magnitude of loading cycles in the fatigue test, traditional error metrics such as mean square error (MSE) or root mean square error (RMSE) may not accurately describe the differences between predicted results and actual experimental data. In cases where the loading amplitude \({F}_{m}\) reaches 700N and the number of fatigue cycles exceeds the order of 106, even a small prediction error of 1% can result in an error value on the order of 104. Under these extreme conditions, MSE and RMSE values become very large and cannot be used to accurately assess the quality of predicted results. Thus, we calculated the correlation coefficient of Pearson first [31]:

$${r}^{\text{peason }}=\frac{\sum_{i=1}^{104}({({N}_{f})}_{\text{pred. }}-\overline{{({N}_{f})}_{\text{pred. }}})({({N}_{f})}_{\text{exp. }}-\overline{{({N}_{f})}_{\text{exp. }}})}{\sqrt{\sum_{i=1}^{104}{({({N}_{f})}_{\text{prod. }}-\overline{{({N}_{f})}_{\text{pwed }}})}^{2}}\sqrt{\sum_{i=1}^{104}{({({N}_{f})}_{\mathrm{exp}}-\overline{{({N}_{f})}_{\text{exp }}})}^{2}}}$$
(34)

Result is: \({r}^{\text{pearson}}\)=0.9794.

Analysis of the experimental data revealed a Pearson correlation coefficient greater than 0.8, indicating a strong correlation between predicted and actual results [31]. Based on this correlation, a random selection of 50 sets of data from the experimental array was used to re-fit the ML model presented in Section 4. The variable x input this time is the previous prediction results. Through this way, the relationship between the prediction result and the test result is found to be significant in Fig. 20:

Fig. 20
figure 20

Prediction results (a) by mathematical formula fitting method, (b) by ML method

Full size image

Here [31]:

$${r}^{2}=1-\frac{\sum_{i=1}^{104}{({({N}_{f})}_{\mathrm{exp}}-{({N}_{f})}_{pred})}^{2}}{\sum_{i=1}^{104}{({({N}_{f})}_{\mathrm{exp}}-\overline{{({N}_{f})}_{\mathrm{exp}}})}^{2}}$$
(35)
$$MAPE=\frac{1}{104}\sum\nolimits_{i=1}^{104}\frac{|{({N}_{f})}_{\mathrm{exp}}-{({N}_{f})}_{pred}|}{{({N}_{f})}_{\mathrm{exp}}}$$
(36)

The mean absolute percentage error (MAPE) and r2 are used here to describe the accuracy of the predictive model. In general, the closer MAPE is to zero and the closer r2 is to one, the higher the prediction accuracy of the model is. It can be seen from the above figure that the predicted results show excellent accuracy in comparison with the experimental results.

In conclusion, the FEA model used in this study is based on elastic calculations using principles of fracture mechanics. In addition, machine learning model was mainly trained on macroscopic experimental conditions. The advantage of this method is that the fatigue life of high-strength steel RSW joints can be predicted with high precision through simple modeling under the premise of known fracture modes. The average error of prediction is approximately 8%. Moreover, the training time of the model is relatively short, which reduces the risk of overfitting.

4.2 Further investigation and discussions

In this study, tensile-shear fatigue tests were conducted on RSW joints following the ISO 14324–2003 standard. During the experimental process, some test factors can also be considered. For example, procedures such as dirt removal and grinding mentioned in literature [24] could be considered. Additionally, the influence of humidity and temperature mentioned in literature [25] should be considered in future studies. Furthermore, the impact of the crosshead speed mentioned in literature [26] is another factor to be taken into account. In this experiment, a fixed frequency of force loading (from maximum to minimum force) was used instead of a fixed crosshead speed. To further enhance the universality of the database in the future, tests with a fixed crosshead speed can be conducted.

In the future investigations, one of the important goals is to expand the database's applicability to encompass a wider range of materials. For example, aluminum alloy 7075 mentioned in literature [32] and biocompatible material Zn–Mg–WC nanocomposites mentioned in literature [33]. These materials provide new evidence for predicting fatigue characteristics from aspects such as chemical composition, hardness, and deformation mechanisms. Another goal is that make the database applicable to a broader range of welding processes. One promising research direction for improving welding quality is nano-treating, which has shown excellent performance in addressing the issue of thermal cracking in high strength aluminum alloys [32]. By introducing titanium carbide (TiC) nanoparticles during the solidification process of the melting zone, nano-treatment modifies the morphology of α-grains and secondary phases in the alloy, resulting in a crack-free fusion joint. The presence of nanoparticles leads to a quasi-spherical grain morphology in the melting zone and eliminates the dendritic grain growth commonly associated with solidification cracking [32]. This indicates that nano-treatment has the ability to control and alter the microstructural features of materials. This provides clues for future design of predictive models. The microstructural features, such as grain size, phase distribution, and grain boundary characteristics, can be considered in FEA models to understand how they influence crack propagation and consequently alter the fatigue behavior of structural components. This can further expand the applicability of predictive models. In the future, the scope of the database can be further expanded based on the impact of such processes on the fatigue performance of the components.

Besides, from the perspective of expanding the data features used by ML models, the future trend is to incorporate the microstructural characteristics of materials, such as hardness, grain boundaries, etc., into consideration [34,35,36]. For example, the interaction mechanisms between dislocation substructures during deformation and solute atoms in high-entropy alloys (HEAs) are discussed in literature [34]. From this perspective, the mechanical performance characteristics associated with alloying elements can be incorporated into an ML model. Also, the method mentioned in literature [35] involves converting the crystal structure of materials into images and designing a convolutional neural network where the nodes correspond to atoms and the edges correspond to atomic bonds as vectors. Then, the features of each atom are combined to form the overall features of the crystal. In this way, sufficient data features can be collected for training purposes for different materials. Undoubtedly, this provides wonderful microscopic clues for expanding the scale of databases in the future.

5 Conclusions

In this study, a model was developed to predict the F-N curves of RSW joints made of high-strength steels. The model was trained by FEA, experimental data, and ML. The learning process led to the following conclusions:

  1. (1)

    The BP neural network learning algorithm exhibited superior accuracy in capturing complex nonlinear relationships compared to traditional mathematical formula-based methods. Overall, the goodness of fit improved by 8.5%, and the MAPE decreased by 13%.

  2. (2)

    When using two different sheet materials, the optimization of the model using the BFGS algorithm resulted in a minimum reduction of 12% in the MAPE.

  3. (3)

    The proposed model was cross-validated according to ISO 14324–2003 standard or similar standards that define fatigue damage. Both trained and untrained experimental data were utilized in the cross-validation process. The average error was found to be 8%, and the goodness of fit was approximately 98%.