Abstract
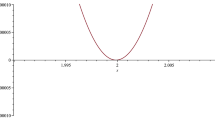
We use the sampling method to compute the eigenvalues of a quadratic pencil. To do so we first prove a non standard representation of the eigensolution that allows us to decompose the characteristic function into Paley-Wiener functions. Numerical examples illustrating the computation by the sampling method of real as well as complex eigenvalues are provided at the end.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
M. H. Annaby, and R. M. Asharabi, Bounds for truncation and perturbation errors of nonuniform sampling series, BIT, 56, no. 3, 807–832, 2016.
M. H. Annaby, and R. M. Asharabi, On sinc-based methods in computing eigenvalues of boundary-value problems, SIAM J. Numer. Anal., 46, no. 2, 671–690, 2008.
M. H. Annaby and M. M. Tharwat, On computing eigenvalues of second-order linear pencils, IMA Journal of Numerical Analysis, 27, 366–380, 2007.
N. Bondarenko and G. Freiling, An inverse problem for the quadratic pencil of non-self-adjoint matrix operators on the half-line, J. Inverse Ill-Posed Probl., 44, no. 4, 467–495, 2013.
A. Boumenir, Eigenvalues of periodic Sturm-Liouville problems by the Shannon-Whittaker sampling, Math. Comp., 68, no. 227, 1057–1066, 1999.
A. Boumenir, Sampling and eigenvalues of non-self-adjoint Sturm-Liouville problems, SIAM J. Sci. Comput., 23, no. 1, 219–229, 2001.
J. B. Conway, Functions of One Complex Variable,(v.1), 2nd ed, Graduate Texts in Mathematics - Vol. 11, Springer, 1978.
S. Cox snd E. Zuazua, The rate at which energy decays In a string damped at one end, Communications in Partial Differential Equations, 19, no. 1–2, 213–243, 1994.
M. G. Gasymov and G. Guseinov, Determination of a diffusion operator from spectral data, (Russian) Akad. Nauk Azerbaidzhan. SSR Dokl., 37, no. 2, 19–23, 1981.
M. Hasanov, The spectra of two-parameter quadratic operator pencils, Math. Comput. Modelling, 54, no. 1–2, 742–755, 2011.
D. Jagerman, Bounds for truncation error of the sampling expansion. SIAM J. Appl. Math., 14, 714–723, 1966.
H. Koyunbakan, Inverse problem for a quadratic pencil of Sturm-Liouville operator. J. Math. Anal. Appl., 378, no. 2, 549–554, 2011.
A. G. Kostyuchenko and A. A. Shkalikov, Self-adjoint quadratic operator pencils and elliptic problems, Funct. Anal. Appl., 17, no. 2, 109–128, 1983.
H. Langer, R. Mennicken and C. Tretter, A self-adjoint linear pencil Q-λP of ordinary differential operators, Methods Funct. Anal. Topology, 2, 38–54, 1996.
B. M. Levitan and M. G. Gasymov, Determination of a differential equation by two of its spectra, Russ. Math. Surveys, 19, 1–62, 1964.
W. W. Lin and J. N. Wang, Partial pole assignment for the quadratic pencil by output feedback control with feedback designs, Numer. Linear Algebra Appl., 12, no. 10, 967–979, 2005.
M. Möller, Self-adjoint quadratic operator pencils and applications, Not. S. Afr. Math. Soc., 45, no. 1, 2–13, 2014.
M. Möller, and V. Pivovarchik, Spectral Theory of Operator Pencils, Hermite-Biehler Functions, and their Applications, Operator Theory: Advances and Applications, 246, Birkhauser/Springer, Cham, 2015.
I. M. Nabiev, Multiplicity and relative position of the eigenvalues of a quadratic pencil of Sturm-Liouville operators, translation in Math. Notes, 67, no. 3–4, 309–319, 2000.
V. N. Pivovarchik, Eigenvalues of a certain quadratic pencil of operators, Funct. Anal. Appl., 23, no. 1, 80–81, 1989.
N. I. Pronska, Asymptotics of eigenvalues and eigenfunctions of energy-dependent Sturm-Liouville equations, Mat. Stud., 40, no. 1, 38–52, 2013.
A. Zayed, Advances in Shannon’s Sampling Theory, CRC Press, 1993.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Baskaya, E., Boumenir, A. Sampling and the Eigenvalues of a Quadratic Pencil. STSIP 18, 9–22 (2019). https://doi.org/10.1007/BF03549618
Published:
Issue Date:
DOI: https://doi.org/10.1007/BF03549618