Abstract
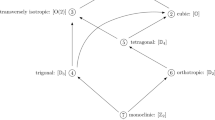
It is shown that all symmetries possible for the elastic tensors can be reduced to the twelve symmetries already used in the description of the crystal classes. Each symmetry can be characterized by a group of rotations generated by no more than two rotations. The use of a canonical basis related to such rotations considerably simplifies the component forms of the elasticity tensor. This result applies to non-symmetric tensors; for symmetric tensors, the number of independent symmetries reduces from twelve to ten.
After the present work was submitted, the following paper came to our attention: 14. S.C. Cowin and M.M. Mehrabadi, On the identification of material symmetry for anisotropic elastic materials. Q. Jl. Mech. appl. Math.40 (1987) 451–476. This paper contains an independent analysis of the partial ordering ≺ among the crystallographic elastic symmetries. However, it does not deal with the problem of the completeness of these symmetries.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
S. Bhagavantam and T. Venkatarayudu, Theory of Groups and its Application to Physical Problems. Academic Press (1969).
B.D. Coleman and W. Noll. Material symmetries and thermostatic inequalities in finite elastic deformations. Arch. Rat. Mech. Analysis 15 (1964) 87–111.
M.E. Gurtin, The linear theory of elasticity. In: Handbuch der Physik, Vol. VIa/2. Springer (1972).
P.R. Halmos, Finite-Dimensional Vector Spaces. Springer (1974).
A.E.H. Love, A Treatise on the Mathematical Theory of Elasticity, 4th edn. Dover (1944).
P. Podio Guidugli and E. Virga, Transversely isotropic elasticity tensors, Proc. Roy. Soc. London A 411 (1987) 85–93.
T.G. Rogers and A.C. Pipkin, Asymmetric relaxation and compliance matrices in linear viscoelasticity. ZAMP 14 (1963) 334–343.
J.A. Schouten, Tensor Analysis for Physicists. Oxford: Clarendon Press (1951).
G.F. Smith and R.S. Rivlin, The strain-energy function for anisotropic elastic materials. Trans. Amer. Math. Soc. 88 (1958) 175–193.
C. Somigliana, Sulla legge di razionalita' rispetto alle proprieta' elastiche dei cristalli. Rend. Accad. Naz. Lincei 3 (1894) 238–246.
W. Voigt, Allgemeine Formeln für die Bestimmung der Elasticitätsconstanten von Krystallen durch die Beobachtung der Biegung und Drillung von Prismen. Ann. Phys. 16 (1882) 273–321, 398–416.
W. Voigt, Lehrbuch der Krystallphysik. Teubner (1928).
E.T. Whittaker, A Treatise on the Analytical Dynamics of Particles and Rigid Bodies, Cambridge Univ. Press, 4th edn. (1960).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Yong-Zhong, H., Del Piero, G. On the completeness of the crystallographic symmetries in the description of the symmetries of the elastic tensor. J Elasticity 25, 203–246 (1991). https://doi.org/10.1007/BF00040927
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00040927